Polias e engrenagens Movimento e freqüência

Objetos móveis que executam movimento circular possuem uma propriedade denominada freqüência. A freqüência indica o número de vezes que o fenômeno se repete na unidade de tempo. Então, medidas usuais de freqüência podem ser: voltas por segundo, rotações por minuto (rpm), etc.

No Sistema Internacional, a unidade é chamada de Hertz (Hz). Por exemplo, um motor elétrico que gira a 3.000 rpm teria a seguinte freqüência:

f = 3000 rotações / 60 segundos = 50 Hz

Veja alguns dos inúmeros casos em que temos movimentos circulares envolvidos: motores de automóveis, brinquedos de parques de diversão, limpadores de pára-brisas automotivos, discos, engrenagens, câmbios de bicicletas e de outros veículos, polias e correntes transmissoras de movimentos, esteiras mecanizadas, etc.

Polias
As polias utilizam correias ou correntes para transmitir movimento de um eixo para outro. Vamos analisar o caso em que duas polias de aros diferentes são ligadas por uma correia de borracha dita inelástica, desprezando o escorregamento que ocasionalmente ocorre entre os corpos das polias e a correia. As polias são de raios Ra e Rb:


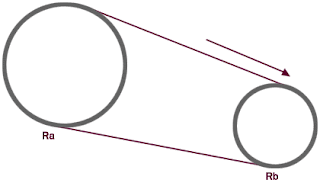
Se não ocorre escorregamento e a polia é inelástica, então todos os pontos da correia e da periferia das polias têm a mesma velocidade escalar.

Então: Va = Vb

Como: V = . R

Podemos dizer que esta é uma relação válida:

a . Ra = b . Rb

Também é possível deixar a relação expressa em função do valor da freqüência (já que = 2 . f):

2 . fa . Ra = 2 . fb . Rb

fa . Ra = fb . Rb

Exemplo: Se trabalhamos com polias de raios de 25 cm e 5 cm respectivamente, quantas rotações por minuto conseguiríamos obter na polia B, se a polia maior (A) girar a 1000 rpm?

Resolução:
fa . Ra = fb . Rb
1000 . 25 = fb . 5
fb = 5000 rpm

Observe que é possível projetar sistemas que reduzam ou ampliem o número de rotações utilizando as polias (ou as engrenagens). É isso que acontece em inúmeras aplicações tecnológicas.

Engrenagens
As engrenagens também têm ampla aplicação na indústria mecânica. Basicamente, elas são discos dentados que podem ser feitos de diversos metais ou ligas resistentes (para serviços mais pesados, como máquinas, câmbios e motores) ou de plástico (para usos mais leves, como em relógios de parede, por exemplo).

Correia dentada de um motor de automóvel.

Por meio da combinação de engrenagens de diferentes características, é possível transmitir movimentos e ampliar ou reduzir forças. Nesse caso, é possível dispensar as correias ou polias, fazendo a transmissão diretamente pelo contato entre as engrenagens:


Para um acoplamento formado por uma engrenagem de raio r e n dentes e outra engrenagem de raio R com N dentes, vale a seguinte relação: r.n = R.N

As engrenagens possuem algumas vantagens sobre outros sistemas, quando se utiliza o funcionamento por meio do contato direto dos dentes:
# Evitam o deslizamento entre as engrenagens, fazendo com que os eixos ligados a elas estejam sempre sincronizados um com o outro.
# Tornam possível determinar relações de marchas exatas. Assim, se uma engrenagem tem 60 dentes e a outra tem 20, a relação de marcha quando elas estão engrenadas é de 3:1.
# São feitas de tal maneira que possam trabalhar mesmo que haja imperfeições no diâmetro e na circunferência reais das duas engrenagens, pois a relação de marcha é controlada pelo número de dentes.
# As bicicletas com câmbio funcionam com um conjunto de discos dentados, acionados por corrente de aço. Conforme mudamos a combinação entre eles, conseguimos mais força ou maior velocidade.

Dica de leitura
Para saber mais sobre as aplicações das engrenagens, leia o texto Como funciona a relação de marchas.

Bibliografia
Curso completo de física. Gerson Herskowicz e Valdemar Scolfaro, Editora Moderna, 1996.
Luis Fábio S. Pucci é professor do Instituto Galileo Galilei para a Educação.