Fração

Para que a apresentação do assunto em um único artigo não fique demasiadamente extenso, ele será dividido em duas ou mais partes. A primeira aborda um pouco de história das frações, cujo texto foi extraído da Wikipédia, sua definição e alguns conceitos e propriedades básicas. Nas próximas trataremos da redução, da simplificação e das operações com frações.

Um pouco de História

“No antigo Egito, por volta do ano 3000 a.C., o faraó Sesóstris distribuiu algumas terras às margens do rio Nilo para alguns agricultores privilegiados. O privilégio em possuir essas terras era porque todo ano, no mês de julho, as águas do rio inundavam essa região ao longo de suas margens e fertilizava os campos. Essas terras, portanto, eram bastante valorizadas.
Porém, era necessário remarcar os terrenos de cada agricultor em setembro, quando as águas baixavam. Os responsáveis por essa marcação eram os agrimensores, que também eram chamados de estiradores de corda, pois mediam os terrenos com cordas nas quais uma unidade de medida estava marcada.
Essas cordas eram esticadas e se verificava quantas vezes a tal unidade de medida cabia no terreno, mas é só parar para pensar um pouquinho para descobrir que nem sempre essa medida cabia inteira nos lados do terreno.
Esse problema só foi resolvido quando os egípcios criaram um novo número: o número fracionário. Ele era representado com o uso de frações, porém os egípcios só entendiam a fração como uma unidade (ou seja, frações cujo numerador é igual a 1).
Eles escreviam essas frações com uma espécie de sinal oval escrito em cima do denominador. Mas os cálculos eram complicados, pois no sistema de numeração que usavam no Egito nessa época os símbolos se repetiam muitas vezes.
Só ficou mais fácil trabalhar com as frações quando os hindus criaram o Sistema de Numeração Decimal, quando elas passaram a ser representadas pela razão de dois números naturais.
Desde então, as frações foram usadas para a resolução de diversos tipos de problemas matemáticos. Uma das formas mais correntes de se trabalhar com frações é a porcentagem, em que se expressa uma proporção ou uma relação a partir de uma fração cujo denominador é 100. O uso de frações também é de valia extrema para a resolução de problemas que envolvem regra de três.”

Definição

Fração é um número que designa uma ou mais partes iguais de uma unidade e sua representação genérica é:

onde a é o numerador e b o denominador e indicam os termos da fração.
O denominador (b) de uma fração estabelece em quantas partes iguais foi dividida a unidade e o numerador (a) quantas destas partes contém a fração.
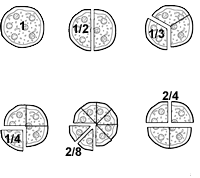
Assim, se dividirmos a unidade em 5 partes iguais e tomarmos 1, 2, 3 ou 7 partes teremos as frações a seguir representadas:

Observe que, ainda considerando esse exemplo, se tomarmos 5 partes obtemos como resultado a própria unidade.

Leitura das Frações

Para se ler uma fração, enuncia-se primeiro seu numerador e depois o denominador de acordo com as seguintes regras:

• Quando o denominador é igual a 2, 3, 4, 5, 6, 7, 8 ou 9 lêem-se meio, terço, quarto, quinto, sexto, sétimo, oitavo ou nono, respectivamente. Exemplo : lê-se dois terços;
• Quando o denominador é maior do que 9 acrescenta-se a terminação avos. Por exemplo, , lê-se cinco onze avos;
• Os denominadores múltiplos ou potências de 10 podem ser lidos, por exemplo, como décimo – ou dez avos -, vigésimo, centésimo, milésimo. Exemplo : lê-se dois décimos. As frações cujos denominadores é uma potência de 10 – isto é, a unidade seguida de um ou mais zeros – são denominadas decimais: (sete décimos), (setenta e oito centésimos), (duzentos e trinta e dois milésimos);
• Costuma-se também, na leitura, intercalar a palavra sobre, depois de enunciar o numerador. A fração pode ser lida como duzentos e trinta e dois sobre cinco mil, quatrocentos e setenta e sete.

Comparação das frações com a unidade

Uma fração é inferior à unidade – menor do que 1 – quando seu numerador é menor do que seu denominador. Nestes casos as frações são denominadas próprias. Exemplos: , e .
Uma fração é superior à unidade – maior do que 1 – quando seu numerador é maior do que seu denominador. Nestes casos as frações são denominadas impróprias. Exemplo: , e . Um caso particular de fração imprópria, denominada de aparente, ocorre quando o numerador é múltiplo do denominador. Exemplo: .

Comparação das frações entre si

Da definição de fração resulta:

• De duas frações de mesmo denominador a maior é a que tem o numerador maior. Exemplo: \frac 59" alt="\frac 89 > \frac 59" style="vertical-align: middle; margin-top: -4px;">. Porque tendo as frações o mesmo denominador significa que a unidade foi dividida no mesmo número de partes iguais. Como a primeira tem o numerador maior – 8 – significa que ela tem mais partes do que a segunda, cujo numerador é 5.
• De duas frações de mesmo numerador a maior é a que tem o denominador menor. Exemplo: \frac {5}{13}" alt="\frac 59 > \frac {5}{13}" style="vertical-align: middle; margin-top: -4px;">. Nesse caso – e de forma geral -, como as frações têm o mesmo numerador (5), elas possuem o mesmo número de partes da unidade, e como o nono da unidade é maior do que o treze avos segue-se que a primeira fração é maior do que a segunda.
• De duas frações próprias entre cujos termos existe a mesma diferença, a maior é aquela cujos termos são maiores. Exemplo: \frac 57" alt="\frac 79 > \frac 57" style="vertical-align: middle; margin-top: -4px;">. Observe que na primeira fração faltam 2/9 para igualar a unidade e na segunda, 2/7. Pela regra anterior 2/9 é menor do que 2/7, logo 7/9 é a fração maior pois lhe falta menos para completar a unidade.

Propriedades das Frações

Propriedade 1. Uma fração representa o quociente da divisão do numerador pelo denominador.
Utilizaremos um exemplo prático para demonstrar a propriedade. Seja a fração 2/5, que segundo a propriedade deve representar o quociente de 2 por 5.
Observe inicialmente que 1/5 somado 5 vezes reproduz a unidade – decorrência da definição de fração. Logo, 2/5 somado 5 vezes darão 2 unidades, e, portanto a fração 2/5 representa o quociente de 2 por 5, pois multiplicada por 5 tem como resultado 2.
Propriedade 2. Quando uma divisão deixa um resto, pode-se completar o quociente por uma fração que tem por numerador o resto da divisão e por denominador o divisor.
Seja dividir 37 por 4 (= 37/4). Essa divisão tem como quociente 9 e resto 1. Assim podemos escrever:

37 = (9×4) + 1 = 36 + 1

Logo:

Observações:

• Na expressão acima na passagem da segunda igualdade foi utilizada a propriedade distributiva da divisão;
• A representação assinalada dentro do retângulo é denominada de número misto ou fração mista e lê-se nove inteiros e um quarto e, como o próprio nome sugere, é composta de uma parte inteira e outra fracionária;
• Uma fração mista é uma outra forma de representar uma fração imprópria;
• A operação inversa – transformar uma fração mista em uma fração imprópria – é feita multiplicando-se o número inteiro (9) pelo denominador (4) e somando o resultado ao numerador (1) para obter o numerador da fração imprópria (37) e o seu denominador é o mesmo da parte fracionária do número misto (4).

Propriedade 3. O valor de uma fração é o quociente da divisão do numerador pelo denominador.
Na definição geral de fração o numerador a e o denominador b podem ter qualquer valor. Assim, as expressões a seguir são consideradas como frações:

e são designadas geralmente como frações compostas. E o valor de uma fração composta é a fração simples que lhe é igual. Nos exemplos acima as frações compostas tem como valor 16/15 e 21/40, respectivamente.
Propriedade 4. Multiplicando-se ou dividindo o numerador de uma fração por um número, a fração é multiplicada ou dividida por esse número
Propriedade 5. Multiplicando-se ou dividindo-se o denominador de uma fração por um número, a fração e dividida ou multiplicada pelo número.
Propriedade 6. Multiplicando-se ou dividindo-se os dois termos – numerador e denominador – por um mesmo número a fração não se altera.
De fato, multiplicando o numerador de uma fração qualquer pelo número c, a fração é multiplicada por c pela propriedade 4, e, multiplicando-se o denominador por c a fração é dividida por c pela propriedade 5. Logo a fração não muda ou não se altera uma vez que é multiplicada e dividida pelo mesmo número c.
Por raciocínio analógo demonstra-se a propriedade para o caso da divisão. Esta propriedade é bastante utilizada na solução de problemas, em especial na racionalização de denominadores de frações irracionais.
Referências:
Elementos de Aritmética, Curso Superior – Para o curso colegial e admissão às escolas superiores, do Irmão Isidoro Dumont, Coleção de Livros Didáticos F. T. D, publicado em 26/10/1945