Esta matéria aborda o conceito e propriedades de sequência ou sucessão, com ênfase nas que possui uma fórmula bem definida que permite calcular qualquer um de seus termos. Ou seja, das sequências que possuem uma lei de formação que estabelece uma relação entre o valor de seus termos e sua posição.
Especificamente, das duas mais conhecidas: a Progressão Aritmética (PA) e a Progressão Geométrica (PG), dividido em três partes (a primeira este artigo e as demais serão publicadas oportunamente):
Um conjunto ordenado é um conjunto que possui uma relação de ordem.
E uma relação de ordem é definida para pares de elementos de um conjunto S, e têm que, necessariamente, possuir três características:
A título de ilustração, abrindo um parênteses, apresento a seguir a fórmula recursiva que define os números de Fibonacci (n pertencente ao conjunto dos números Naturais):

Na prática: você começa com 0 e 1, e então produz o próximo número de Fibonacci somando os dois anteriores.
A representação de uma sequência é feita escrevendo-se seus elementos, ou termos, entre parênteses. Assim, o segundo exemplo acima, é representado por:
Formalmente, uma sequência ou sucessão numérica pode ser definida como uma função dos números naturais menos o zero em R:

Uma sequência numérica é finita se o domínio de f é finito, isto é, i varia de 1 a n pertencente ao conjunto dos números Naturais (i = 1, 2, …, n), também conhecida como n-upla. E infinita quando o domínio é o próprio conjunto dos números Naturais positivos (i = 1, 2, …., n-1, n, …).
Três termos consecutivos qualquer de uma sequência podem ser representados por:
Estas leis de formação podem ser apresentadas das maneiras a seguir:
a) Por Recorrência
São dadas duas ou mais regras: uma (ou mais) que define os termos iniciais da sequência e outra para calcular os demais termos a partir de antecessores.
Exemplos:
Exemplos:
Exemplos:
Uma PA é crescente quando r > 0, ou seja, quando cada termo é maior do que seu antecessor (claro, a partir do segundo). De fato, da definição decorre que:
Sabemos, da definição de uma PA, que a diferença entre cada termo e seu antecessor é igual a razão, isto é:
Da definição vem que:
PA1. Em uma PA finita, a soma de dois termos equidistantes dos extremos é igual à soma dos extremos.
Demonstração:
Sejam ap e aq dois termos equidistantes dos extremos de uma PA finita com n termos. O que vamos provar é:

Demonstração:
Pela propriedade PA1 temos que (note que a soma de todos os índices de cada parcela é igual a n + 1, e portanto, equidistantes dos extremos):

Demonstração:
Consequência direta de PA2, uma vez que a1 = 1 e an = n.
Referências:
Especificamente, das duas mais conhecidas: a Progressão Aritmética (PA) e a Progressão Geométrica (PG), dividido em três partes (a primeira este artigo e as demais serão publicadas oportunamente):
- Parte I – teoria sobre PA;
- Parte II – teoria sobre PG;
- Parte III – exercícios resolvidos sobre PA e PG.
Sequências ou Sucessões
Uma sequência ou sucessão é um conjunto ordenado (finito ou infinito) de elementos de qualquer natureza, em que cada elemento fica naturalmente seqüenciado.Um conjunto ordenado é um conjunto que possui uma relação de ordem.
E uma relação de ordem é definida para pares de elementos de um conjunto S, e têm que, necessariamente, possuir três características:
- anti-simetria: para todo
 e
e 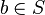 ,
,  ou
ou 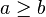 ;
;
- se
 e
e 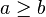 , então
, então  ;
;
- transitividade: se
 e
e  , então
, então 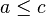 .
.
- sequência dos dias da semana: domingo; segunda-feira; terça-feira; quarta-feira; quinta-feira; sexta-feira; sábado;
- sequência dos 100 primeiros números inteiros positivos: 1; 2; 3; … ; 98; 99; 100;
- Os números de Fibonacci (esta seqüência foi descrita primeiramente por Leonardo de Pisa, também conhecido como Fibonacci (c. 1200), para descrever o crescimento de uma população de coelhos): 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946…
A título de ilustração, abrindo um parênteses, apresento a seguir a fórmula recursiva que define os números de Fibonacci (n pertencente ao conjunto dos números Naturais):
Na prática: você começa com 0 e 1, e então produz o próximo número de Fibonacci somando os dois anteriores.
A representação de uma sequência é feita escrevendo-se seus elementos, ou termos, entre parênteses. Assim, o segundo exemplo acima, é representado por:
(1; 2; 3; … ; 98; 99; 100)
Da definição de sequência, onde a ordem de seus elementos é uma condição necessária, temos que:
( 1; 3; 5; 7; 9; 11) é diferente de (1; 3; 7; 5; 9; 11)
Genericamente, sua representação pode ser escrita como:
(a1; a2; a3; …; an-1; an; …)
onde n pertence ao conjunto dos números naturais positivos. Os índices indicam a posição dos termos na sequência (a1 representa o primeiro termo, an representa o enésimo termo, …).Formalmente, uma sequência ou sucessão numérica pode ser definida como uma função dos números naturais menos o zero em R:
Uma sequência numérica é finita se o domínio de f é finito, isto é, i varia de 1 a n pertencente ao conjunto dos números Naturais (i = 1, 2, …, n), também conhecida como n-upla. E infinita quando o domínio é o próprio conjunto dos números Naturais positivos (i = 1, 2, …., n-1, n, …).
Três termos consecutivos qualquer de uma sequência podem ser representados por:
an-1, an, an+1
onde an-1 é o antecessor de an e an+1 é o sucessor de an.Lei de Formação
Interessam à Matemática as sequências numéricas para as quais é possível estabelecer uma lei de formação, ou seja uma fórmula que permita calcular qualquer um de seus termos. Ou em outras palavras as sequências numéricas em que seus termos se sucedem obedecendo a uma regra.Estas leis de formação podem ser apresentadas das maneiras a seguir:
a) Por Recorrência
São dadas duas ou mais regras: uma (ou mais) que define os termos iniciais da sequência e outra para calcular os demais termos a partir de antecessores.
Exemplos:
- Os números de Fibonacci: definidos a1 = 0 e a2 = 1 e a regra F(n-1) + F(n-2) que corresponde à soma dos dois antecessores para definir os demais termos;
- a1 = 5, an = an-1 + 3 e n = 5: a1 = 5, a2 = a1 + 3 = 8, a3 = a2 + 3 = 11, a4 = a3 + 3 = 14, a5 = a4 + 3 = 17 => (5; 8; 11; 14; 17)
Exemplos:
- an = 2n + 3, n = 1, 2, 3, 4, 5: (5; 7; 9; 11; 13);
- an = 2n, n Natural diferente de zero: (2; 4; 8; 16; …).
Exemplos:
- A sequência cujos termos são os primeiros cinco números primos: (2; 3; 5; 7; 11);
- A sequência dos números inteiros ímpares menores do que 20: (1; 3; 5; 7; 9; 11; 13; 15; 17; 19).
Progressões Aritméticas (PA)
Define-se progressão aritmética como toda sequência numérica em que cada termo, a partir do segundo, é igual à soma de seu antecessor por um número constante r. r é denominado a razão da PA. Em símbolos:
an = an-1 + r (n >= 2)
As PA são classificadas em três tipos:Uma PA é crescente quando r > 0, ou seja, quando cada termo é maior do que seu antecessor (claro, a partir do segundo). De fato, da definição decorre que:
an – an-1 = r > 0 <==> an – an-1 > 0 <==> an > an-1
Uma PA é constante quando r = 0, ou seja, quando cada termo é igual ao antecessor:
an – an-1 = r = 0 <==> an – an-1 = 0 <==> an = an-1
Uma PA é decrescente quando r <>
an – an-1 = r <> an – an-1 <> an <>n-1
Fórmula do Termo Geral de uma PA
Seja (a1; a2; a3; …; an-1; an; …) uma PA qualquer de razão r. Então seu enésimo termo (an) é:
an = a1 + (n – 1)r
Demonstração:Sabemos, da definição de uma PA, que a diferença entre cada termo e seu antecessor é igual a razão, isto é:
a2 – a1 = r, a3 – a2 = r, a4 – a3 = r, …, an – an-1 = r
Somando, membro a membro, estas n – 1 igualdades, obtemos:
a2 – a1 + a3 – a2 + a4 – a3 + … + an – an-1 = (n – 1)r
Cancelando os termos comuns:
-a1 + an = (n – 1)r => an = a1 + (n – 1)r
Observações:- Da definição decorre que uma PA fica determinada quando conhecemos o primeiro termo e a razão;
- Em uma PA finita a1 e an são denominados os seus extremos e os demais termos os meios aritméticos;
- A fórmula do termo geral de uma PA nos diz que para calcular o termo de ordem n é suficiente somarmos (n – 1) vezes a razão ao primeiro termo;
- Do mesmo modo, essa fórmula permite calcular o número de termos de uma PA finita conhecendo-se seus extremos e a razão.
Termos Equidistantes dos Extremos
Dados os dois termos ap e aq de uma PA finita com n termos, dizemos que eles são equidistantes dos extremos se o número de termos que antecedem ap – (p – 1) termos – é igual ao número de termos que sucedem aq – (n – q) termos.Da definição vem que:
p – 1 = n – q => p + q = n + 1
Essa relação nos permite dizer, por exemplo, que em uma PA finita com 30 termos, o termo 6 é equidistante do 25, uma vez que 6 + 25 = 30 + 1.Soma dos termos de uma PA finita
Antes de deduzir a fórmula da soma dos n primeiros termos de uma PA finita, vamos demonstrar a seguinte propriedade:PA1. Em uma PA finita, a soma de dois termos equidistantes dos extremos é igual à soma dos extremos.
Demonstração:
Sejam ap e aq dois termos equidistantes dos extremos de uma PA finita com n termos. O que vamos provar é:
ap + aq = a1 + an
Pela fórmula do termo geral:
ap = a1 + (p – 1)r e aq = a1 + (q – 1)r
Somando os membros das igualdades obtemos:
ap + aq = a1 + (p – 1)r + a1 + (q – 1)r = a1 + a1 + (p + q – 2)r
Substituindo p + q (veja definição acima):
ap + aq = a1 + a1 + (n + 1 – 2)r = a1 + a1 + (n – 1)r
E pela definição do termo geral de uma PA:
ap + aq = a1 + an
PA2. A soma dos n primeiros termos de uma PA é dada pela fórmula:Demonstração:
Pela propriedade PA1 temos que (note que a soma de todos os índices de cada parcela é igual a n + 1, e portanto, equidistantes dos extremos):
a2 + an-1 = a3 + an-2 = … = a1 + an
Por outro lado:
Sn = a1 + a2 + … + an
=> Sn + Sn = 2Sn = (a1 + an) + (a2 + an-1) + … + (an + a1)
onde ordenamos as parcelas convenientemente, primeiro termo do primeiro Sn com o último do segundo, e assim por diante, de modo a obter n parcelas iguais a a1 + an. Logo:
2Sn = (a1 + an)n => Sn = [(a1 + an)n]/2 c.q.d.
PA3. A soma dos n primeiros inteiros positivos é:Demonstração:
Consequência direta de PA2, uma vez que a1 = 1 e an = n.
Referências:
- Fundamentos de Matemática Elementar, Gelson Iezzi, Osvaldo Dolce & Carlos Murakami, São Paulo, Atual Editora Ltda, edição 1977;
- Matemática para o Ensino Médio: Volume Único, Manoel Jairo Bezerra, São Paulo, Editora Scipione, 2001
Comentários
Postar um comentário