Funções do Movimento Uniformemente Variado

No Movimento Uniformemente Variado (MUV), a velocidade escalar é variável e a aceleração é constante e não nula.

Vejamos agora as funções que permitem a descrição matemática do movimento.

Velocidade em Função do Tempo [v = f (t)]

Seja um móvel percorrendo, com MUV uma trajetória retilínea:
A aceleração média do móvel no intervalo de tempo é:



Em que a_m = a = constante



Em que:

v₀: velocidade inicial do móvel;
t₀: instante inicial;
v: a velocidade do móvel no instante t;
a: aceleração;
t: tempo.

Observe que esta função é do 1° grau em relação a t (o que significa que o gráfico da velocidade em função do tempo é representado por uma reta).

Posição em Função do Tempo [s = f (t)]

Seja um móvel percorrendo, com MUV uma trajetória retilínea:
O gráfico da função v = v₀ + at, fornece o espaço percorrido Δs no intervalo de tempo Δt = t – t₀.





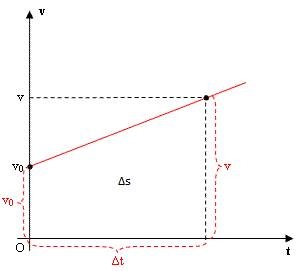
Como v = v0 + at e Δs = s – s0, substituindo-se em (I):





Observe que esta função é do 2° grau em relação a t.

Aceleração em Função do Tempo [a = f (t)]

a = f (t) = constante ≠ 0
Portanto a aceleração em todo o percurso é a mesma do início dele.

Equação de Torricelli

Temos até agora duas funções que nos permitem saber a posição do móvel e a sua velocidade em relação ao tempo. Torna-se útil encontrar uma fórmula que possibilite conhecer a velocidade de um móvel sem saber o tempo.

A equação e Torricelli relaciona a velocidade com o espaço percorrido pelo móvel. É obtida eliminando-se o tempo entre as funções horárias da posição e da velocidade.





Isolando-se o tempo t na segunda igualdade:



Substituindo t em (I):







Reduzindo-se ao mesmo denominador:






Fonte: Site Fazendo Matemática