Determinantes

Determinantes

P₁₀) Quando, em uma matriz, os elementos acima ou abaixo da diagonal secundária são todos nulos, o determinante é igual ao produto dos elementos dessa diagonal multiplicado por .
Exemplos:

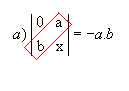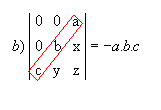P₁₁) Para A e B matrizes quadradas de mesma ordem n, . Como: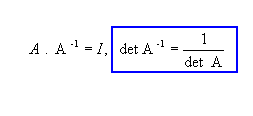

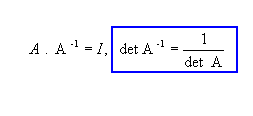
Exemplo:

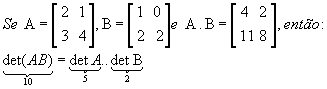
P₁₂)

Exemplo:

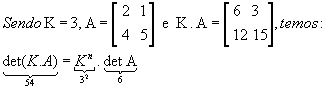
P₆) O determinante de uma matriz e o de sua transposta são iguais.

Exemplo:

P₇) Multiplicando por um número real todos os elementos de uma fila em uma matriz, o determinante dessa matriz fica multiplicado por esse número.

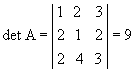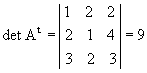Exemplos:

P₈) Quando trocamos as posições de duas filas paralelas, o determinante de uma matriz muda de sinal.
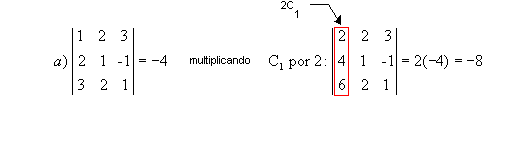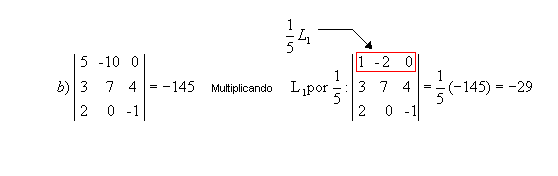Exemplo:

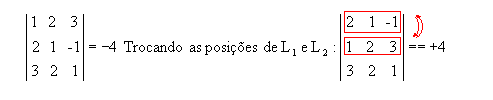
P₉) Quando, em uma matriz, os elementos acima ou abaixo da diagonal principal são todos nulos, o determinante é igual ao produto dos elementos dessa diagonal.
Exemplos:

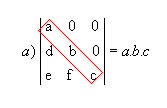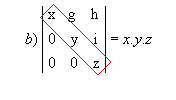Propriedades dos determinantes

Os demais associados a matrizes quadradas de ordem n apresentam as seguintes propriedades:

P₁ ) Quando todos os elementos de uma fila ( linha ou coluna) são nulos, o determinante dessa matriz é nulo.

Exemplo:

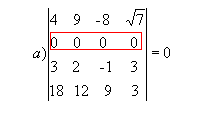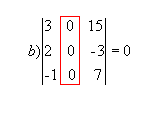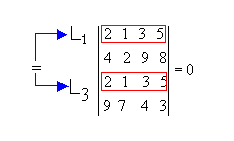
P₂) Se duas filas de uma matriz são iguais, então seu determinante é nulo.

Exemplo:

P₃) Se duas filas paralelas de uma matriz são proporcionais, então seu determinante é nulo.

Exemplo:

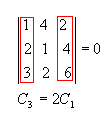
P₄) Se os elementos de uma fila de uma matriz são combinações lineares dos elementos correspondentes de filas paralelas, então seu determinante é nulo.

Exemplos:

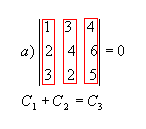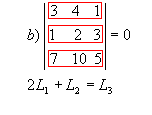P₅ ) Teorema de Jacobi: o determinante de uma matriz não se altera quando somamos aos elementos de uma fila uma combinação linear dos elementos correspondentes de filas paralelas.

Exemplo:

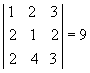
Substituindo a 1ª coluna pela soma dessa mesma coluna com o dobro da 2ª, temos:

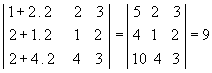
6ª propriedade

O valor do determinante de uma matriz R é igual ao determinante da matriz da transposta de R, det R = det (R ^t).

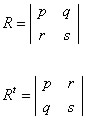
det R = ps + qr

det Rt = ps – rq


7ª propriedade
Ao trocarmos duas linhas ou duas colunas de posição de uma matriz, o valor do seu determinante passa a ser oposto ao determinante da anterior.



8ª propriedade

O determinante de uma matriz triangular é igual à multiplicação dos elementos da diagonal principal.
Lembre-se que em uma matriz triangular, os elementos acima ou abaixo da diagonal principal são iguais a zero.

9ª propriedade
Considerando duas matrizes quadradas de ordem iguais e AB matriz produto, temos que: det (AB) = (det A) * (det B), conforme teorema de Binet.


10ª propriedade

Ao multiplicarmos todos os elementos de uma linha ou de uma coluna pelo mesmo número e adicionarmos os resultados aos elementos correspondentes de outra linha ou coluna, formamos a matriz B, onde ocorre a seguinte igualdade: det A = det B. Esse teorema é atribuído a Jacobi.