Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
O triângulo é considerado o polígono mais simples da geometria plana e o mais importante, levando em consideração as características de seu formato. Estruturas de sustentação são construídas no formato triangular, em razão da segurança obtida.
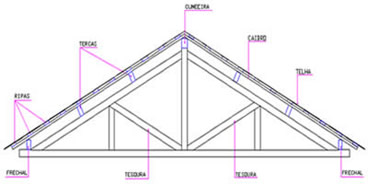
Observe a utilização de triângulos
na sustentação de telhados.
na sustentação de telhados.
Por ser um polígono, o triângulo possui perímetro (soma das medidas dos lados) e área. No caso dos triângulos, a área é medida através da metade do produto da base pela altura, de acordo com a fórmula: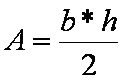 
, com b medida da base e h medida da altura. Existem três modelos de triângulos quanto à medida dos seus lados:
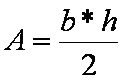, com b medida da base e h medida da altura. Existem três modelos de triângulos quanto à medida dos seus lados:
Escaleno: os lados possuem medidas diferentes.
Isósceles: possui dois de seus lados com medidas iguais.
Equilátero: possui todos os lados com mesma medida.
Isósceles: possui dois de seus lados com medidas iguais.
Equilátero: possui todos os lados com mesma medida.
Nosso trabalho enfatizará a área de um triângulo equilátero. Observe o triângulo de vértices A, B e C com lados medindo a e altura h.
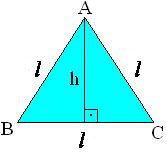
Nesse caso não sabemos a medida da altura, que deverá ser calculada através do Teorema de Pitágoras. Veja:
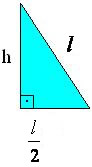
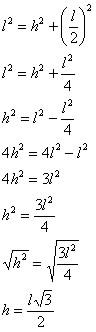
De acordo com a medida da altura h calculada, determinaremos a área do triângulo equilátero com base na seguinte fórmula:
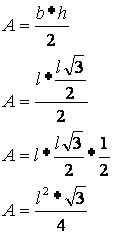
Veja que a expressão determinada calcula a área de qualquer triângulo equilátero com base na medida de seu lado.
Exemplo 1
Determine a medida da área de uma região triangular equilátera, com lados medindo 12 metros de comprimento.
A região triangular possui área medindo 36√3 metros.
Exemplo 2
Qual a medida da lateral de um triângulo equilátero que possui área total medindo 100√3 cm²?
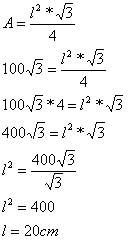
Marcos Noé
Nenhum comentário:
Postar um comentário