Área total do cilindro

Cilindros

O cilindro é um sólido geométrico bastante utilizado na indústria de embalagens e na armazenagem de líquidos em geral. É considerado um corpo redondo por conter uma de suas faces arredondadas. Em razão dessa característica, o cálculo de sua área total requer algumas observações e certo cuidado.

Considere um cilindro circular reto de raio da base r e altura h, como mostra a figura abaixo.

Para compreender como é feito o cálculo de sua área total devemos fazer a planificação do cilindro.

Observe que ao planificar o cilindro obtemos duas circunferências de raio r, relativas às duas bases apresentadas no sólido, e um retângulo de altura h e comprimento 2πr. Podemos concluir que:

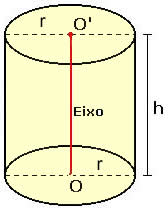
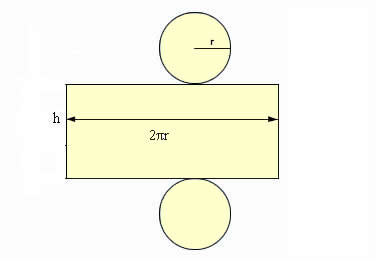
área total = área lateral + área da base + área da base

Como as bases do cilindro são circunferências de raio r, temos que:

área da base = π∙r²

A área lateral é dada por:

área lateral = 2∙π∙r∙h

Assim, podemos determinar a área total de um cilindro da seguinte forma:

S_t = 2∙π∙r∙h + 2∙π∙r²

Colocando 2πr em evidência, obtemos:

S_t = 2∙π∙r∙(h + r)

Que é a fórmula para o cálculo da área total de um cilindro, onde:

S_t → é a área total
r → é a medida do raio da base
h → é a altura do cilindro

Observe que para calcular a área total do cilindro basta conhecer a medida do raio e da altura.

Vejamos alguns exemplos de aplicação da fórmula da área total.

Exemplo 1. Determine a área total de um cilindro circular reto de 16 cm de altura e raio da base medindo 5 cm. (Use π = 3,14)

Solução: Pelo enunciado do problema temos os seguintes dados:
h = 16 cm
r = 5 cm
St = ?

Utilizando a fórmula da área total, obtemos:

S_t=2∙π∙r∙(h+r)
S_t = 2 ∙ 3,14 ∙ 5 ∙(16 + 5)
S_t = 2 ∙ 3,14 ∙ 5 ∙ 21
S_t = 659,4 cm²

Exemplo2. Uma indústria deseja fabricar um barril de óleo com formato cilíndrico cujo raio da base deve apresentar 40 cm de comprimento e sua altura será de 1,2 m. Para fabricação desse barril, a indústria utilizará chapas metálicas. Quantos metros quadrados de chapa serão necessários para fabricar um barril? (Use π = 3,14)

Solução: A resolução desse problema consiste em determinar a área total desse barril, que apresenta o formato de um cilindro. Do enunciado do problema, obtemos:
h = 1,2 m
r = 40 cm = 0,4 m
St = ?

Pela fórmula da área total, temos que:

S_t = 2∙π∙r∙(h + r)
S_t = 2 ∙ 3,14 ∙ 0,4 ∙ (1,2 + 0,4)
S_t = 2 ∙ 3,14 ∙ 0,4 ∙ 1,6
S_t = 4,02 m²

Portanto, serão gastos, aproximadamente, 4,02 metros quadrados de chapa metálica para confeccionar um barril.

Exemplo 3. Uma lata de extrato de tomate de formato cilíndrico possui área total de 244,92 cm² de área total. Sabendo que o raio da base da lata mede 3 cm, obtenha a medida da altura dessa embalagem.

Solução: Pelo enunciado do problema, obtemos:
St = 244,92 cm²
h = ?
r = 3 cm

Utilizando a fórmula da área total, temos que:

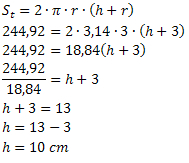
Portanto, a lata possui uma altura de 10 cm.
fonte: www.alunosonline.com.br