Proposição]
Proposição é uma sentença declarativa afirmativa que pode assumir um valor de Verdadeiro (V) ou Falso (F).
Como exemplo de proposições temos:
- A terra é redonda.
- O dado é quadrado.
As proposições, de acordo com a lógica clássica, devem observar os seguintes princípios (entre outros):
- Príncipio da não-contradição: uma proposição não pode ser Verdadeira ou Falsa ao mesmo tempo.
- Príncipio do terceiro excluído: uma proposição deve obrigatoriamente ser Verdadeira ou Falsa, mas não ter uma terceira possibilidade.
Símbolos
Variáveis proposicionais
Dentro da lógica proposicional cada proposição é considerado um elemento simples (átomo), representado com uma letra minúscula a partir do p. (Por exemplo, p, q e outros).
Conectivos lógicos
As fórmulas atômicas podem ser combinadas entre si utilizando-se os conectivos lógicos. Utilizam-se os parênteses para delimitar o alcance de cada conectivo.
| Valor lógico | Símbolo | Expressão | Observação |
|---|---|---|---|
| Negação |  , ¬ , ~ ou ' | não, é falso, não é verdade que | inverte o valor da proposição |
| Conjunção |  | e, mas , também, além disso | nenhuma |
| Disjunção |  | ou | não confundir com o ou exclusivo |
| Condicional |  | se...então, implica, logo, somente se | nenhuma |
| Bi-condicional |  | ...se, e somente se...; ...é condição necessária que ... | nenhuma |
Uma cadeia que forma uma expressão válida (isto é, que ofereça um valor F ou V de retorno) é chamada de fórmula bem-formulada(fbf).
Tabelas-verdades são matrizes de V ou F que uma proposição assume de acordo com o conectivo lógico associado a ele. Utilizaremos a letra p para representar o uso de conectivos sobre apenas uma proposição, e p e q quando o conectivo age sobre duas proposições.
Conjunção
| p | q | p q |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
Disjunção
| p | q | p q |
|---|---|---|
| V | V | V |
| V | F | V |
| F | V | V |
| F | F | F |
Condicional]
| p | q | p  q |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | V |
| F | F | V |
Bi-condicional]
| p | q | p q |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | V |
Disjunção-exclusiva]
| p | q | p q |
|---|---|---|
| V | V | F |
| V | F | V |
| F | V | V |
| F | F | F |
Proposições compostas]
Uma proposição composta é um conjunto de proposições simples com seus conectivos, representada por uma letra maiúscula. Ex: P: pq ou P (p,q):p,q. Para n proposições simples com possibilidades V e F, considera-se que a tabela-verdade que os combina terá 
linhas.
q ou P (p,q):p,q. Para n proposições simples com possibilidades V e F, considera-se que a tabela-verdade que os combina terá linhas.- Tautologia
Tautologia é uma proposição composta onde todas as suas combinações finais são Verdadeiras (V).
- Contradição
Contradição é uma proposição composta onde todas as suas combinações finais são Falsas (F).
- Contingência
Contingência é uma proposição composta onde os valores F e V aparecem pelo menos uma vez nas combinações finais.
Implicação]
Uma proposição implica logicamente outra quando, e somente quando, para cada atribuição de valores verdade que torna uma proposição verdadeira, também tornam sua implicação verdadeira. Ou seja, dadas duas proposições P e Q, P implica Q todas as vezes que ambos os lados aparecerem Ve.
| p | q | (P) pq | (Q)pq | (R) pq |
|---|---|---|---|---|
| V | V | V | V | V |
| V | F | F | V | F |
| F | V | F | V | F |
| F | F | F | F | V |
Equivalência lógica]
Uma proposição composta é logicamente equivalente a outra se suas tabelas-verdades são idênticas. A equivalência lógica é representada por (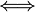
)...,,
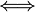)...,,Resumo]
- Cálculo proposicional é um sistema da lógica matemática que representa os príncipios e operações da lógica proposicional .
- Proposição é uma sentença declarativa afirmativa que pode assumir um valor de Verdadeiro (V) ou Falso (F).Uma proposição não pode ser Verdadeira ou Falsa ao mesmo tempo e uma proposição deve obrigatoriamente ser Verdadeira ou Falsa, mas não ter uma terceira possibilidade.
- As fórmulas atômicas podem ser combinadas entre si utilizando-se os conectivos lógicos. Utilizam-se os parênteses para delimitar o alcance de cada conectivo.
- Uma Proposição Composta é um conjunto de proposições simples com seus conectivos, representada por uma letra maiúscula.
- Tautologia é uma proposição composta onde todas as suas combinações finais são V.
- Contradição é uma proposição composta onde todas as suas combinações finais são F.
- Contingência é uma proposição composta onde os valores F e V aparecem pelo menos uma vez nas combinações finais.
- Uma proposição implica logicamente outra quando, e somente quando, para cada atribuição de valores verdade que torna uma proposição verdadeira, também tornam sua implicação verdadeira.
- Uma proposição composta é logicamente equivalente a outra se suas tabelas-verdades são idênticas.
Bibliografia]
- Klement, Kevin C. (2006), "Propositional Logic", in James Fieser and Bradley Dowden (eds.), Internet Encyclopedia of Philosophy,Eprint.
- Introduction to Mathematical Logic
- Elements of Propositional Calculus
- forall x: an introduction to formal logic, por P.D. Magnus, covers formal semantics and proof theory for sentential logic.
Comentários
Postar um comentário