A Variância e o Desvio Padrão são consideradas
medidas de dispersão e utilizadas nas situações em que grupos com médias
de valores iguais, possuem características diferentes. A Variância
estabelece os desvios em relação à média aritmética e o Desvio Padrão
analisa a regularidade dos valores. Vamos através de um exemplo prático,
demonstrar uma aplicação básica envolvendo as duas medidas.
Na preparação para os jogos Olímpicos de Atenas, três atletas do salto em altura ao realizarem um treinamento diário, consideraram seus quatro melhores saltos em centímetros. Veja:
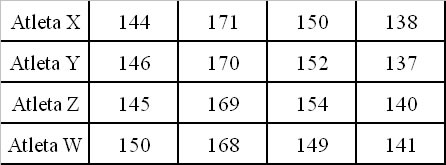
Dentre os atletas, a melhor média foi a do Atleta Z, veja:
Atleta X = (144 + 171 + 150 + 138) / 4 = 150,75
Atleta Y = (146 + 170 + 152 + 137) / 4 = 151,25
Atleta Z = (145 + 169 + 154 + 140) / 4 = 152
Atleta W = (150 + 167 + 149 + 141) / 4 = 151,75
Em situações que envolvam disputas olímpicas, o atleta com melhor média, às vezes não é considerado o mais indicado, pois verifica-se a questão da regularidade dos resultados obtidos. É referente a esses casos que aplicamos os cálculos ligados à Variância e ao Desvio Padrão.
Lembre-se de que o desvio padrão consiste na raiz quadrada da variância.
Cálculo da Variância e do Desvio Padrão
Na preparação para os jogos Olímpicos de Atenas, três atletas do salto em altura ao realizarem um treinamento diário, consideraram seus quatro melhores saltos em centímetros. Veja:

Dentre os atletas, a melhor média foi a do Atleta Z, veja:
Atleta X = (144 + 171 + 150 + 138) / 4 = 150,75
Atleta Y = (146 + 170 + 152 + 137) / 4 = 151,25
Atleta Z = (145 + 169 + 154 + 140) / 4 = 152
Atleta W = (150 + 167 + 149 + 141) / 4 = 151,75
Em situações que envolvam disputas olímpicas, o atleta com melhor média, às vezes não é considerado o mais indicado, pois verifica-se a questão da regularidade dos resultados obtidos. É referente a esses casos que aplicamos os cálculos ligados à Variância e ao Desvio Padrão.
Lembre-se de que o desvio padrão consiste na raiz quadrada da variância.
Cálculo da Variância e do Desvio Padrão
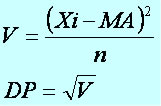
Atleta X

Atleta Y

Atleta Z
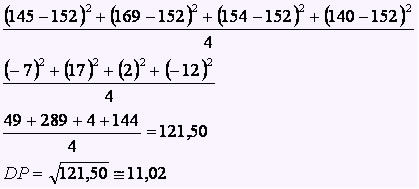
Atleta W

O atleta que obteve o menor Desvio Padrão deve ser considerado o de melhor regularidade em resultados. Dessa forma, temos que o atleta W se enquadra nessa condição de melhor regularidade.
Comentários
Postar um comentário