Maria se exercita regularmente em sua bicicleta, por 30 minutos. Sua meta, em cada sessão, é gastar, no mínimo, 420 kcal. Depois de se exercitar por 20 minutos, ela observa no mostrador que já gastou 240 kcal. Para cumprir seu objetivo, ela deve aumentar a intensidade do exercício nos próximos 10 minutos de maneira a aumentar o dispêndio de calorias por minutos em relação à média dos primeiros 20 minutos em:
A) 25%
B) 30%
C) 50%
D) 60%
E) 80%
Solução:
Meta: 420 kcal em 30’
Gastou: 240kcal em 20’: 240/20= 12kcal/min
Ele deve gastar mais 180 kcal em 10’: 18kcal/min
Fazendo 18kcal-12kcal=6kcal
Usamos uma regra de três simples:
12kcal----100%
6kcal-----x
X=50%
Resp.: C
QUESTÃO 2
Marcos quer pintar os vértices, numerados de 1 a 6 no sentido anti-horário, de um hexágono regular dispondo, para isto, de 4 cores, com as seguintes restrições:
a) Dois vértices vizinhos devem ter cores distintas,
b) Dois vértices opostos devem ter a mesma cor.
De quantas maneiras distintas ele pode fazer isto? (Duas pinturas são distintas se algum dos vértices numerados foi pintado com cores diferentes).
A) 12
B) 24
C) 30
D) 60
E) 72
Solução:
Essa solução eu fiz usando a figura:
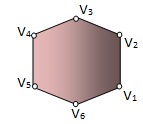 |
4 possibilidades para V1
3 possibilidades para V2 ,
2 possibilidades para V3
V4, V5, V6 tem a mesma cor de V2, V1 e V3, respectivamente, restando para eles apenas uma possibilidade.
Logo, pelo Princípio Fundamental da Contagem, temos: 4x3x2x1=24 modos distintos
Resp: B
QUESTÃO 3
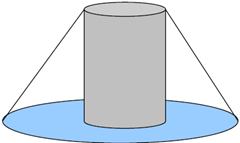
Uma broca de raio r = 2 perfura um cone circular reto de altura H = 12 e raio R = 6
ao longo de seu eixo central. O resultado é um tronco de cone perfurado conforme
ilustrado acima. O volume do buraco cilíndrico é então:
A) 16π
B) 20π
C) 24π
D) 28π
E) 32π
Solução:
Vamos analisar a figura:
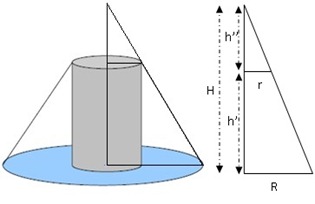 |
Sabendo que:
Usando o volume do cilindro, encontramos:
Resposta: E

Solução:
Devemos substituir os valores de (x1,y1)=(3,1) e (x2,y2)=(4,3) em (y1-ax1)2+(y2-ax2)2
Fica assim:
(1-a.3)2+(3-a.4)2=1-6a+9a2+9-24a+16a2=25a2-30a+10 = 5a2-6a+2
Que resultou numa função quadrática com gráfico cuja concavidade é voltada para cima. Portanto, devemos encontrar o valor mínimo de x que será encontrado usando Xv=-b/2a
Temos:
Letra A
5ª QUESTÃO
A um vendedor foi fixada uma meta de fazer um certo número de abordagens e também uma meta de sucesso de venda de 60% das abordagens. Quando havia realizado 75% das abordagens, o vendedor contabilizou um sucesso de 56% sobre as abordagens já realizadas, e percebeu que deveria aumentar sua porcentagem de sucessos nos 25% restantes para conseguir atingir a meta. Quanto deve ser o percentual de sucessos sobre o restante das abordagens para que ele consiga atingir a meta de sucesso fixada inicialmente?
A) 100%
B) 90%
C) 80%
D) 72%
E) 64%
Solução: A) 100%
B) 90%
C) 80%
D) 72%
E) 64%
Total de abordagens: X
Meta de Sucesso: 60% de X = 0,6X
Quando realizou 75% das abordagens, ou seja 0,75X, teve sucesso de 56%. Portanto, devemos fazer:
56% de 0,75X = 0,42X
Faltam, então 0,6X – 0,42X = 0,18X, ou seja, 18% do total de abordagens.
Sabendo que restam apenas 25%=0,25 de abordagens para serem realizadas, usamos uma regra de três simples:
0,25--------100%
0,18---------y
Resultando em y = 18/0,25=72%
Resposta: D
Questão 08
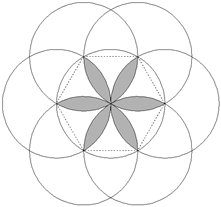
Um arquiteto desenhou a rosácea da figura, produzida por interseções de seis círculos de raios iguais centrados sobre os vértices de um hexágono regular inscrito num círculo de mesmo raio. O arquiteto pretende fazer o desenho de forma tal que os círculos tenham 10 m de raio, num grande paredão, e para calcular a tinta necessária precisa estimar a área da rosácea (que está sombreada no desenho). Entre as cinco alternativas abaixo, aquela que melhor estima a área da rosácea é:
A) 50m2
B) 80m2
C) 110m2
D) 160m2
E) 310m2
Solução: A) 50m2
B) 80m2
C) 110m2
D) 160m2
E) 310m2
Calculamos inicialmente ÁREA DO CÍRCULO(Ac) -ÁREA DO HEXÁGONO(Ah):
Sabendo que l=r=10m e considerando π=3,14 e raiz quadrada de 2 igual a 1,73, temos:
![clip_image002[20] clip_image002[20]](https://lh5.ggpht.com/_fSsSaKPmd2s/TVgRulPqrLI/AAAAAAAAAwk/cWlsy3GafAw/clip_image002%5B20%5D_thumb%5B3%5D.gif?imgmax=800)
Multiplicando por 2 encontramos a área da rosácea:
Área Rosácea = 54,5x2=109m2
Portanto, o valor mais próximo está na letra C.
Fonte:http://jonasportal.blogspot.com/
Obrigado amigo por citar o meu blog! Muito grato! Pena q estou sem tempo para atualizá-lo!!! Vou ter q me dedicar mais a ele!
ResponderExcluirO que voçês acharam do nível do profmat 2012 em relação ao 2011 ?
ResponderExcluir