segunda-feira, 4 de novembro de 2019
Modulo de um número
Podemos dizer que módulo é o mesmo que distância de um número real ao número zero, pois o módulo de número real surgiu da necessidade de medir a distância de um número negativo ao zero.
Ao medirmos a distância de um número negativo qualquer ao zero percebe-se que a distância fica negativa e como não é usual dizer que uma distância ou comprimento é negativo foi criado o módulo de número real que torna o valor positivo ou nulo.
Assim, podemos dizer que o módulo de um número real irá seguir duas opções:
• O módulo ou valor absoluto de um número real é o próprio número, se ele for positivo.
• O módulo ou valor absoluto de um número real será o seu simétrico, se ele for negativo.
A representação de um módulo ou valor absoluto de um número real é feito por duas barras paralelas.
Veja o resumo da definição de módulo de um número real abaixo:
|x| = x, se x ≥ 0
-x, se x < 0
Veja alguns exemplos de como calcular módulo ou valor absoluto de números reais.
• |+4| = 4
• |-3| = - (-3) = 3
• |10 – 6 | = |+4| = 4
• |-1 – 3| = |-4| = - (-4) = 4
• |-1| + |5| - |6| = -(-1) + 5 – 6 = 1 + 5 - 6 = 6 – 6 = 0
• - | -8| = -[-(-8)] = - 8
Veja alguns exemplos de como encontrar o módulo de valores desconhecidos.
• |x + 2| nesse caso teremos duas opções, pois não sabemos o valor da incógnita x. Assim, seguimos a definição:
x + 2, se x + 2 ≥ 0, ou seja, x ≥ -2
- (x + 2), se x + 2 < 0, ou seja, x < -2
• |2x – 10|
2x – 10, se 2x – 10 ≥ 0, ou seja, 2x ≥ 10 → x ≥ 5
-(2x – 10), se 2x – 10 < 0, ou seja, 2x < 10 → x < 5
• |x2 – 9|
x 2 – 9, se x2 – 9 ≥ 0
x 2 – 9 ≥ 0
x 2 ≥ 9
x ≥ 3 ou x ≤ -3
- (x 2 – 9) , se x2 – 9 < 0
x2 – 9 < 0
x2 < 9
-3 < x < 3
Ao medirmos a distância de um número negativo qualquer ao zero percebe-se que a distância fica negativa e como não é usual dizer que uma distância ou comprimento é negativo foi criado o módulo de número real que torna o valor positivo ou nulo.
Assim, podemos dizer que o módulo de um número real irá seguir duas opções:
• O módulo ou valor absoluto de um número real é o próprio número, se ele for positivo.
• O módulo ou valor absoluto de um número real será o seu simétrico, se ele for negativo.
A representação de um módulo ou valor absoluto de um número real é feito por duas barras paralelas.
Veja o resumo da definição de módulo de um número real abaixo:
|x| = x, se x ≥ 0
-x, se x < 0
Veja alguns exemplos de como calcular módulo ou valor absoluto de números reais.
• |+4| = 4
• |-3| = - (-3) = 3
• |10 – 6 | = |+4| = 4
• |-1 – 3| = |-4| = - (-4) = 4
• |-1| + |5| - |6| = -(-1) + 5 – 6 = 1 + 5 - 6 = 6 – 6 = 0
• - | -8| = -[-(-8)] = - 8
Veja alguns exemplos de como encontrar o módulo de valores desconhecidos.
• |x + 2| nesse caso teremos duas opções, pois não sabemos o valor da incógnita x. Assim, seguimos a definição:
x + 2, se x + 2 ≥ 0, ou seja, x ≥ -2
- (x + 2), se x + 2 < 0, ou seja, x < -2
• |2x – 10|
2x – 10, se 2x – 10 ≥ 0, ou seja, 2x ≥ 10 → x ≥ 5
-(2x – 10), se 2x – 10 < 0, ou seja, 2x < 10 → x < 5
• |x2 – 9|
x 2 – 9, se x2 – 9 ≥ 0
x 2 – 9 ≥ 0
x 2 ≥ 9
x ≥ 3 ou x ≤ -3
- (x 2 – 9) , se x2 – 9 < 0
x2 – 9 < 0
x2 < 9
-3 < x < 3
Equação Fundamental da Reta
Podemos determinar a equação fundamental de uma reta utilizando o ângulo
formado pela reta com o eixo das abscissas (x) e as coordenadas de um
ponto pertencente à reta. O coeficiente angular da reta, associado à
coordenada do ponto, facilita a representação da equação da reta.
Observe:
Considerando uma reta r, o ponto C(xC, yC) pertencente à reta, seu coeficiente angular m e outro ponto D(x,y) genérico diferente de C. Com dois pontos pertencentes a reta r, um real e outro genérico, podemos calcular o seu coeficiente angular.
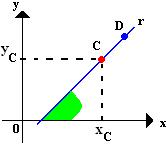
m = y – y0/x – x0
m (x – x0) = y – y0
Portanto, a equação fundamental da reta será determinada pela seguinte expressão:
y – y0 = m (x – x0)
Exemplo 1
Encontre a equação fundamental da reta r que possui o ponto A (0,-3/2) e coeficiente angular igual a m = – 2.
y – y0 = m (x – x0)
y – (–3/2) = –2(x – 0)
y + 3/2 = –2x
2x + y + 3/2 = 0
Exemplo 2
Obtenha uma equação para a reta representada abaixo:
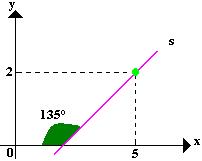
Para determinarmos a equação fundamental da reta precisamos das coordenadas de um dos pontos pertencentes à reta e o valor do coeficiente angular. As coordenadas do ponto fornecido é (5,2), o coeficiente angular é a tangente do ângulo α.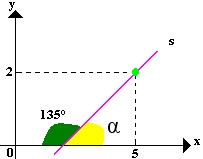
Iremos obter o valor de α com a diferença 180° – 135° = 45°, então α = 45º e a tg 45° = 1.
y – y0 = m (x – x0)
y – 2 = 1 (x – 5)
y – 2 = x – 5
y – x + 3 = 0
Exemplo 3
Determine a equação da reta que passa pelo ponto de coordenadas (6; 2) e possui inclinação de 60º.
Coeficiente angular é dado pela tangente do ângulo 60º: tg 60º = √3.
y – y0 = m (x – x0)
y – 2 = √3 (x – 6)
y – 2 = √3x – 6√3
–√3x + y – 2 + 6√3 = 0
√3x – y + 2 – 6 √3 = 0
Marcos Noé
Considerando uma reta r, o ponto C(xC, yC) pertencente à reta, seu coeficiente angular m e outro ponto D(x,y) genérico diferente de C. Com dois pontos pertencentes a reta r, um real e outro genérico, podemos calcular o seu coeficiente angular.
m = y – y0/x – x0
m (x – x0) = y – y0
Portanto, a equação fundamental da reta será determinada pela seguinte expressão:
y – y0 = m (x – x0)
Exemplo 1
Encontre a equação fundamental da reta r que possui o ponto A (0,-3/2) e coeficiente angular igual a m = – 2.
y – y0 = m (x – x0)
y – (–3/2) = –2(x – 0)
y + 3/2 = –2x
2x + y + 3/2 = 0
Exemplo 2
Obtenha uma equação para a reta representada abaixo:
Para determinarmos a equação fundamental da reta precisamos das coordenadas de um dos pontos pertencentes à reta e o valor do coeficiente angular. As coordenadas do ponto fornecido é (5,2), o coeficiente angular é a tangente do ângulo α.
Iremos obter o valor de α com a diferença 180° – 135° = 45°, então α = 45º e a tg 45° = 1.
y – y0 = m (x – x0)
y – 2 = 1 (x – 5)
y – 2 = x – 5
y – x + 3 = 0
Exemplo 3
Determine a equação da reta que passa pelo ponto de coordenadas (6; 2) e possui inclinação de 60º.
Coeficiente angular é dado pela tangente do ângulo 60º: tg 60º = √3.
y – y0 = m (x – x0)
y – 2 = √3 (x – 6)
y – 2 = √3x – 6√3
–√3x + y – 2 + 6√3 = 0
√3x – y + 2 – 6 √3 = 0
Marcos Noé
juros compostos
Os juros compostos são somados ao capital para o cálculo de novos juros nos tempos posteriores, o chamado juros sobre juros.
Observe o exemplo a seguir:
Pedro aplicou R$ 300,00 num banco que paga juros compostos de 3% ao mês. Qual será seu montante após o período de 6 meses?
O montante após 6 meses de aplicação será de R$ 358,21.
Exemplo 2
Qual o montante produzido por um capital de R$ 2.000,00, aplicado a juros compostos de 2% ao mês, durante um ano?
Fórmula para o cálculo de juros compostos M = C*(1 + i)t , onde:
M = montante
C = capital
i = taxa
t = tempo
Dados
M = ?
C = 2000
i = 2% = 2/100 = 0,02
t = 1 ano = 12 meses (pois a taxa é ao mês)
M = C* (1 + i)t
M = 2000* (1+0,02)12
M = 2000 * 1,0212
M = 2000*1,268242
M = 2.536,48
O montante produzido ao final de um ano será de R$ 2.536,48.
Exemplo 3
Qual deve ser o capital que, no sistema de juros compostos, à taxa de 4% ao mês, gera um montante de R$ 12.154,90 ao final de 1 ano e 6 meses?
M = 12.154,90
C = ?
i = 4% = 4/100 = 0,04
t = 1 ano e 6 meses = 18 meses
M = C* (1 + i)t
12.154,90 = C * (1 + 0,04)18
12.154,90 = C * 1,0418
12.154,90 = C * 2,0258
C = 12.154,90 / 2,0258
C = 6.000
O capital será de R$ 6.000,00.
Exemplo 4
Calcule o montante de um capital de R$ 12.000,00 aplicado durante 3 anos em um banco que paga no regime de juros compostos uma taxa de 1,5% a.m.
M = ?
C = 12.000
i = 1,5% = 1,5/100 = 0,015
t = 3 anos = 36 meses (pois a taxa de juros é mensal)
M = C* (1 + i)t
M = 12000 * (1 + 0,015)36
M = 12000 * 1,01536
M = 12000 * 1,70914
M = 20.509,68
O montante será de R$ 20.509,68.
Exemplo 5
O capital de R$ 1.500,00, aplicado a juros compostos, rendeu, após 2 meses, juros de R$ 153,75. Qual foi a taxa de juros?
M = 1500 + 153,75 = 1653,75
M = C * (1 + i)t
1653,75 = 1500 * (1 + i) 2
1653,75 / 1500 = (1 + i) 2
(1 + i) 2 = 1,1025
√(1 + i) 2 = √1,1025 (use a calculadora para extrair a raiz quadrada de 1,1025)
1 + i = 1,05
i = 1,05 – 1
i = 0,05 ou 5%
A taxa de juros empregada foi de 5%.
/www.mundoeducacao.com.br
Observe o exemplo a seguir:
Pedro aplicou R$ 300,00 num banco que paga juros compostos de 3% ao mês. Qual será seu montante após o período de 6 meses?
O montante após 6 meses de aplicação será de R$ 358,21.
Exemplo 2
Qual o montante produzido por um capital de R$ 2.000,00, aplicado a juros compostos de 2% ao mês, durante um ano?
Fórmula para o cálculo de juros compostos M = C*(1 + i)t , onde:
M = montante
C = capital
i = taxa
t = tempo
Dados
M = ?
C = 2000
i = 2% = 2/100 = 0,02
t = 1 ano = 12 meses (pois a taxa é ao mês)
M = C* (1 + i)t
M = 2000* (1+0,02)12
M = 2000 * 1,0212
M = 2000*1,268242
M = 2.536,48
O montante produzido ao final de um ano será de R$ 2.536,48.
Exemplo 3
Qual deve ser o capital que, no sistema de juros compostos, à taxa de 4% ao mês, gera um montante de R$ 12.154,90 ao final de 1 ano e 6 meses?
M = 12.154,90
C = ?
i = 4% = 4/100 = 0,04
t = 1 ano e 6 meses = 18 meses
M = C* (1 + i)t
12.154,90 = C * (1 + 0,04)18
12.154,90 = C * 1,0418
12.154,90 = C * 2,0258
C = 12.154,90 / 2,0258
C = 6.000
O capital será de R$ 6.000,00.
Exemplo 4
Calcule o montante de um capital de R$ 12.000,00 aplicado durante 3 anos em um banco que paga no regime de juros compostos uma taxa de 1,5% a.m.
M = ?
C = 12.000
i = 1,5% = 1,5/100 = 0,015
t = 3 anos = 36 meses (pois a taxa de juros é mensal)
M = C* (1 + i)t
M = 12000 * (1 + 0,015)36
M = 12000 * 1,01536
M = 12000 * 1,70914
M = 20.509,68
O montante será de R$ 20.509,68.
Exemplo 5
O capital de R$ 1.500,00, aplicado a juros compostos, rendeu, após 2 meses, juros de R$ 153,75. Qual foi a taxa de juros?
M = 1500 + 153,75 = 1653,75
M = C * (1 + i)t
1653,75 = 1500 * (1 + i) 2
1653,75 / 1500 = (1 + i) 2
(1 + i) 2 = 1,1025
√(1 + i) 2 = √1,1025 (use a calculadora para extrair a raiz quadrada de 1,1025)
1 + i = 1,05
i = 1,05 – 1
i = 0,05 ou 5%
A taxa de juros empregada foi de 5%.
/www.mundoeducacao.com.br
Prisma
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Áreas
A área de um polígono que forma uma face lateral do prisma recebe o nome de área de uma face lateral.
Quando as faces laterais tiverem a mesma área, o prisma será regular.
A soma das áreas das faces laterais de um prisma é denominada área lateral.
A soma das áreas das faces de um prisma é denominada área total.
Desta maneira, considerando Al , como sendo a área lateral de um prisma, Ab como sendo a área de uma das bases e At como sendo a área total, teremos:
extraido de www.colegioweb.com.br
Assinar:
Postagens (Atom)