Solução de um Sistema Utilizando a Regra de Cramer

Dado o sistema:

2x + 8y = 0
9x + 6y = 15

Notemos que a matriz incompleta desse sistema é:

2 8
9 6

Onde o determinante é dado por D = 2*6 – 8*9 →12 – 72 → – 60
Verificamos que o D ≠ 0, então o sistema é possível e determinado.

A solução desse sistema será dada por:

x = Dx / D e y = Dy / D

Onde Dx e Dy são obtidos trocando a coluna x ou a y (de acordo com a que está calculando) pela coluna dos termos independentes. Observe:

Calculando Dx:

0 8
15 6


0*6 – 8*15 = – 120

x = Dx / D = – 120/– 60 = 2
x = 2

Calculando Dy:

2 0
9 15

2*15 – 0*9 = 30

y = Dy / D = 30 / – 60 = – 0,5
y = – 0,5

Resolva o sistema a seguir aplicando a Regra de Cramer.

2x + 4y + 2z = 18
4x + 2y – 2z = 6
6x – 2y – 4z = - 8
Obtendo a Matriz incompleta:
2 4 2
4 2 -2
6 -2 -4

Obtendo D: (aplicar regra de Sarrus)

2 4 2 2 4
4 2 -2 4 2
6 -2 -4 6 -2

[-16 + (-48) + (-16)] – [ -64 + 8 + 24]
-16 -48 -16 +64 -8 -24
-48

Calculando x:
Dx:
18 4 2 18 4
6 2 -2 6 2
-8 -2 -4 -8 -2

-144 + 64 – 24 + 96 – 72 + 32
-48


x = Dx / D = -48/-48 = 1
x = 1

Calculando y:
Dy:
2 18 2 2 18
4 6 -2 4 6
6 -8 -4 6 -8

-48 -216 -64 +288 -32 -72
-144

y = Dy / D = -144/-48 = 3
y = 3

Calculando z:
Dz:
2 4 18 2 4
4 2 6 4 2
6 -2 -8 6 -2

-32 +144 -144 +128 +24 -216
-96

z = Dz / D = -96 / -48 = 2
z = 2

O terno ordenado (1, 3, 2) satisfaz o sistema.
www.mundoeducacao.com.br

Regra de chió

Regra de Chió

Através dessa regra é possível abaixar em uma unidade a ordem de uma matriz quadrada A sem alterar o valor do seu determinante.
A regra prática de Chió consiste em:

a) Escolher um elemento a_ij = 1 (caso não exista, aplicar as propriedades para que apareça o elemento 1).

b) Suprimir a linha (i) e a coluna (j) do elemento a_ij = 1, obtendo-se o menor complementar do referido elemento.

c) Subtrair de cada elemento do menor complementar obtido o produto dos elementos que ficam nos pés das perpendiculares traçadas do elemento considerado às filas suprimidas.

d) Multiplicar o determinante obtido no 3.º item por (-1)_i+j onde i e j designam as ordens da linha e da coluna às quais pertence o elemento a_ij = 1.


www.colegioweb.com.br

Determinantes: Regra de Sarrus

Pierre Frederic SARRUS (1798 - 1861), foi professor na universidade francesa de Strasbourg. São escassas, e eu diria, inexistentes, as informaçoes sobre o Prof. SARRUS nos livros de Matemática do segundo Grau, que Apresentamo (ou mais simplesmente apenas citam) o nome do professor, na forma REGRA DE SARRUS, para o cálculo dos determinantes de terceira Ordem.

A regra de SARRUS, foi provávelmente escrita no ano de 1833. O Prof. SARRUS, foi premiado Pela Academia Francesa de Ciências, Pela autoria de UM trabalho que versava sobre as integrais múltiplas.

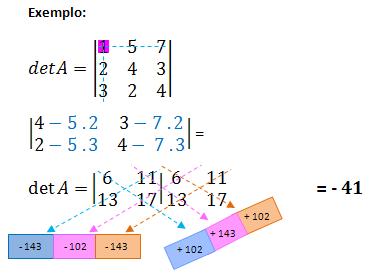
Cálculo do determinante de 3ª Ordem através da Regra de Sarrus .

Este cálculo pode ser feito da seguinte maneira:

Acompanhe como aplicamos Essa regra para .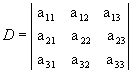

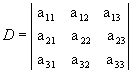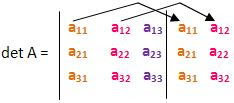
1º Passo : Repetimos as duas primeiras colunas do lado da terceira:

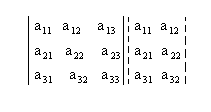
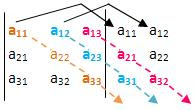
2º Passo : Encontramos a soma do produto dos elementos da diagonal principal com os Dois produtos obtidos Pela multiplicação dos elementos das paralelas a Essa diagonal (a soma Deve ser precedida do sinal positivo):

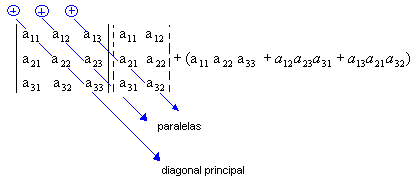
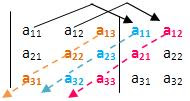
3º Passo : Encontramos a soma do produto dos elementos da diagonal secundária com os Dois produtos obtidos Pela multiplicação dos elementos das paralelas a Essa diagonal (a soma Deve ser precedida do sinal negativo):

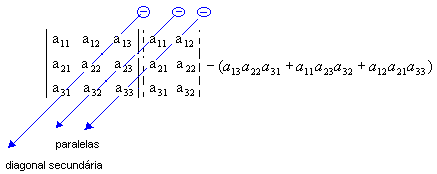
Assim:

Observação: Se desenvolvermos ESSE determinante 3ª Ordem aplicando o Teorema de Laplace, encontraremos o mesmo número real.

Determinante de Ordem n> 3

Vimos que a regra de Sarrus é válida para o cálculo do determinante de umha matriz de Ordem 3. Quand a matriz é de Ordem superior a 3, devemos usar o Teorema de Laplace para chegar a determinantes de Ordem 3 e depois aplicar a regra de Sarrus .

Referência:

Site: Algo Sobre Vestibular.

Site: Só Matemática.

Aranha

Reino: Animália
Filo: Arthropoda
Classe: Arachnida
Ordem: Araneae

As aranhas não são insetos, diferenciam-se dos mesmos pelas seguintes características: não possuem asas ou antenas; têm quatro pares de pernas; produzem teia. A aranha é um animal artrópode, existem cerca de 40.000 espécies de aranhas.

As aranhas respiram através de filotraquéias, pulmões foliares. Seu corpo é dividido em cefalotórax e abdômen. Alimentam-se de líquidos.

O estudo das aranhas denomina-se aracnologia.

Apesar de todas as aranhas possuírem glândulas produtoras de veneno, poucas são perigosas.

O veneno da aranha interrompe a informação entre o sistema nervoso e os músculos, provocando paralisia.

O tratamento sintomático é à base de anestésicos e analgésicos.
www.mundoeducacao.com.br

TABELA DE RAZÕES TRIGONOMÉTRICAS

Tatiane Pietrobelli

Progressão Aritmética PA; termo geral

Determinantes

Determinantes

P₁₀) Quando, em uma matriz, os elementos acima ou abaixo da diagonal secundária são todos nulos, o determinante é igual ao produto dos elementos dessa diagonal multiplicado por .
Exemplos:

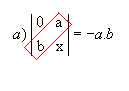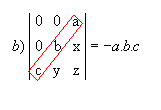P₁₁) Para A e B matrizes quadradas de mesma ordem n, . Como: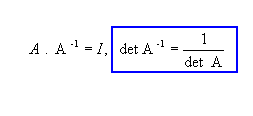

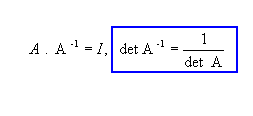
Exemplo:

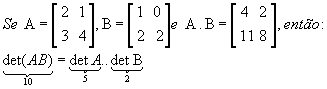
P₁₂)

Exemplo:

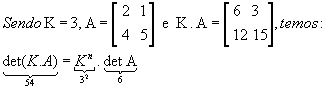
P₆) O determinante de uma matriz e o de sua transposta são iguais.

Exemplo:

P₇) Multiplicando por um número real todos os elementos de uma fila em uma matriz, o determinante dessa matriz fica multiplicado por esse número.

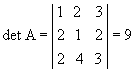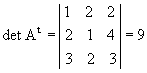Exemplos:

P₈) Quando trocamos as posições de duas filas paralelas, o determinante de uma matriz muda de sinal.
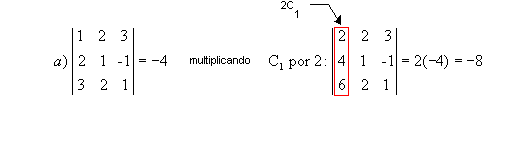Exemplo:

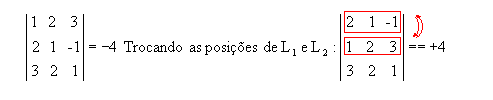
P₉) Quando, em uma matriz, os elementos acima ou abaixo da diagonal principal são todos nulos, o determinante é igual ao produto dos elementos dessa diagonal.
Exemplos:

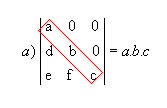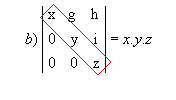Propriedades dos determinantes

Os demais associados a matrizes quadradas de ordem n apresentam as seguintes propriedades:

P₁ ) Quando todos os elementos de uma fila ( linha ou coluna) são nulos, o determinante dessa matriz é nulo.

Exemplo:

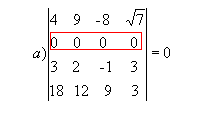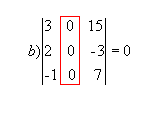P₂) Se duas filas de uma matriz são iguais, então seu determinante é nulo.

Exemplo:

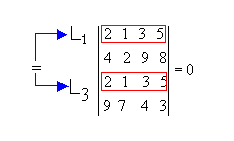
P₃) Se duas filas paralelas de uma matriz são proporcionais, então seu determinante é nulo.

Exemplo:

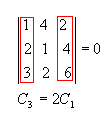
P₄) Se os elementos de uma fila de uma matriz são combinações lineares dos elementos correspondentes de filas paralelas, então seu determinante é nulo.

Exemplos:

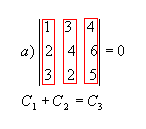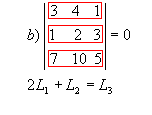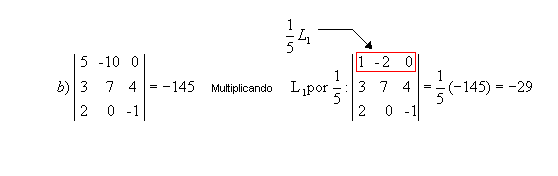
P₅ ) Teorema de Jacobi: o determinante de uma matriz não se altera quando somamos aos elementos de uma fila uma combinação linear dos elementos correspondentes de filas paralelas.

Exemplo:

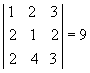
Substituindo a 1ª coluna pela soma dessa mesma coluna com o dobro da 2ª, temos:

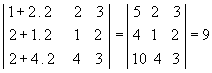
6ª propriedade

O valor do determinante de uma matriz R é igual ao determinante da matriz da transposta de R, det R = det (R ^t).

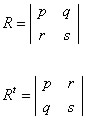
det R = ps + qr

det Rt = ps – rq


7ª propriedade
Ao trocarmos duas linhas ou duas colunas de posição de uma matriz, o valor do seu determinante passa a ser oposto ao determinante da anterior.



8ª propriedade

O determinante de uma matriz triangular é igual à multiplicação dos elementos da diagonal principal.
Lembre-se que em uma matriz triangular, os elementos acima ou abaixo da diagonal principal são iguais a zero.

9ª propriedade
Considerando duas matrizes quadradas de ordem iguais e AB matriz produto, temos que: det (AB) = (det A) * (det B), conforme teorema de Binet.


10ª propriedade

Ao multiplicarmos todos os elementos de uma linha ou de uma coluna pelo mesmo número e adicionarmos os resultados aos elementos correspondentes de outra linha ou coluna, formamos a matriz B, onde ocorre a seguinte igualdade: det A = det B. Esse teorema é atribuído a Jacobi.

Calculo de determinante

O detA de uma matriz de ordem 3 pode ser calculado utilizando uma regra prática chamada Regra de Sarrus, onde repetem-se, à direita da matriz, as duas primeiras colunas. Acompanhando as flechas em diagonal, multiplicam-se os elementos entre si, associando-lhes o sinal indicado.

Vamos fazer por partes:

Matrizes e determinantes

Matrizes formam um importante conceito em matemática, de especial uso no estudo de transformações lineares. Não é o propósito desta página a teoria dessas transformações, mas apenas alguns fundamentos e operações básicas com matrizes que as representam.

Uma matriz A_m,n pode ser entendida como um conjunto de mn (m multiplicado por n) números, dispostos em m linhas e n colunas, conforme figura ao lado.

Portanto, na matriz abaixo, de 2 linhas e 3 colunas, temos:

Adição e subtração

Esta operação só pode ser feita com matrizes de mesmo número de linhas e mesmo número de colunas.

Multiplicação por um escalar

Algumas propriedades das operações anteriores

Sejam A e B matrizes m,n e c e d escalares. Então:
c (A + B) = cA + cB e d (cA) = dc (A).
E, também, se cA = cB então A = B.

Matrizes nulas e unitárias

Multiplicação de matrizes

Sejam as matrizes A_m,p e B_p,n (o número de colunas da primeira deve ser igual ao número de linhas da segunda). O produto AB é dado pela matriz C_m,n cujos elementos são calculados por:

c11 = 4.1 + 0.2 + 5.1 = 9 | c12 = 4.2 + 0.5 + 5.0 = 8 |
c21 = 1.1 + 1.2 + 3.1 = 6 | c22 = 1.2 + 1.5 + 3.0 = 7 |

Temos então a fórmula genérica:

Ordem dos fatores

Se A e B são matrizes quadradas (igual número de linhas e colunas), ambos os produtos AB e BA podem ser calculados.

Entretanto, na multiplicação de matrizes, a ordem dos fatores não é indiferente.
Em geral AB ? BA. Se AB = BA, as matrizes são ditas comutativas.

Algumas propriedades do produto de matrizes

Sejam as matrizes A, B e C.
1) Se os produtos A(BC) e (AB)C são possíveis de cálculo, então A(BC) = (AB)C.
2) Se os produtos AC e BC são possíveis, então (A+B)C = AC + BC.
3) Se os produtos CA e CB são possíveis, então C(A+B) = CA + CB.
4) Se I_p é a matriz unitária pp conforme já mencionado, então: I_p A_p,n = A_p,n e B_m,p I_p = B_m,p.

Matriz inversa

Sejam as matrizes quadradas A_n,n e B_n,n. Se BA = I_n , onde I_n é a matriz unitária conforme já visto, então B é chamada de matriz inversa esquerda de A.

Para achar a matriz inversa:

Por exemplo, seja a matriz A ao lado e desejamos saber sua inversa esquerda B.


O primeiro passo é acrescentar uma matriz unitária no lado direito de A.
Agora, o objetivo é somar ou subtrair linhas multiplicadas por coeficientes de forma a obter a matriz unitária no lado esquerdo (processo de Gauss-Jordan).

1ª linha = 1ª linha + 2ª linha multiplicada por -1.

2ª linha = 2ª linha + 1ª linha multiplicada por -1.
3ª linha = 3ª linha + 1ª linha multiplicada por -2.

3ª linha = 3ª linha + 2ª linha multiplicada por -3.

3ª linha = 3ª linha multiplicada por -1.

2ª linha = 2ª linha + 3ª linha multiplicada por -1.

E a matriz inversa é a parte da direita.

Determinantes de 2ª ordem

O conceito de determinante está ligado ao de matriz, embora seja completamente distinto: enquanto matriz é o conjunto de elementos conforme já mencionado, determinante é o resultado de uma operação aritmética com os elementos de uma matriz, que obedece a uma determinada regra. Só se aplica a matrizes quadradas.

Veja ao lado para uma matriz A_2,2 (determinante de 2ª ordem).
O prefixo det é colocado antes da matriz para indicar determinante. Ou, de forma mais compacta, os colchetes na matriz são substituídos por barras verticais para o mesmo efeito.

Determinantes de ordens superiores

Para determinantes de 3ª ordem ou superior, o cálculo pode ser feito pela decomposição: considera-se, por exemplo, a primeira linha da matriz e somam-se as parcelas de cada elemento desta linha multiplicado pelo determinante da matriz que restar pela eliminação da linha e coluna que passam pelo elemento.

Se o índice da coluna for par, o sinal da parcela será negativo e positivo do contrário. Para cada determinante restante, o processo é repetido até chegar a determinantes de 2ª ordem, que são calculados pela fórmula anterior.
A figura acima demonstra o método para um determinante de terceira ordem.

Algumas propriedades dos determinantes

1) Mantidas as ordens dos elementos, um determinante não se altera se linhas e colunas são trocadas.

2) Se duas linhas ou duas colunas são trocadas entre si, o determinante muda de sinal.

3) Se os elementos de duas linhas ou colunas são iguais entre si, proporcionais entre si ou nulos, o determinante é nulo (k é um número qualquer).

4) Se os elementos de uma mesma linha ou coluna têm um fator de multiplicação comum, ele pode ser colocado em evidência.

5) Um determinante não se altera se aos elementos de uma linha ou coluna são somados ou subtraídos os elementos (ou múltiplos deles) de outra linha ou coluna.

Exemplo de aplicação de determinantes

Seja o sistema de equações lineares ao lado e o determinante B calculado pelos coeficientes das variáveis.

E os determinantes conforme figura a lado.
Então a solução é dada por: x = B1/B, y = B2/B e z = B3/B.

Fonte: www.mspc.eng.br