Números Diretamente Proporcionais

Os números de uma sequência numérica serão diretamente proporcionais aos números de outra sequência se a razão entre eles de forma respectiva possuir o mesmo resultado. Por exemplo, vamos verificar se os números da sequência (2, 3, 5) são diretamente proporcionais aos números da sequência (10, 15, 25). Veja:

Observe que as razões possuem o mesmo valor. Dessa forma, dizemos que os números das sequências são diretamente proporcionais.

Em algumas situações, os cálculos são realizados no intuito de determinar valores desconhecidos das sequências numéricas, a fim de tornar os números diretamente proporcionais. Observe os exemplos:

Exemplo 1

Vamos calcular o valor de a e b nas sequências (a, 8, 10) e (24, 32, b), considerando que os números sejam diretamente proporcionais.

Exemplo 2

Determine o valor de x e y nas sequências (15, x, 42) e (90, 180, y) de modo que eles sejam diretamente proporcionais.

Os cálculos apresentados são de grande utilidade na divisão diretamente proporcional. Veja:

João quer dividir 60 balas de doce entre três crianças, de forma que a distribuição seja realizada de forma diretamente proporcional às suas idades que são 2, 3 e 5 anos.

De acordo com as idades 2, 3 e 5 elas receberão 12, 18 e 30 balas, respectivamente.
www.bancodeconcursos.com

Juros simples

Juros Simples

Quando compramos uma mercadoria a prazo, normalmente, pagamos uma compensação em dinheiro correspondente ao número de
prestações.

Quando depositamos dinheiro na Caderneta de Poupança ou num fundo de aplicação financeira, estamos emprestando dinheiro ao
banco e dele recebemos uma compensação em dinheiro pelo tempo que o dinheiro estiver com o banco.

A compensação financeira ou acréscimo em dinheiro é o que denominamos de Juros e corresponde a uma porcentagem do capital
emprestado.

Quando alugamos um carro, um filme em DVD, ou mesmo, um apartamento, pagamos por esse empréstimo um aluguel. Juro é o
aluguel de dinheiro.

O que nos permite escrever:

Juro é uma quantia que se recebe como compensação pelo empréstimo de dinheiro.


O dinheiro que se empresta ou se toma emprestado chama-se Capital e se representa por C.

A duração desse empréstimo chama-se Tempo e se representa por t.

A compensação obtida por um capital se chama Juro e se representa por j.

A taxa percentual obtida com um empréstimo chama Taxa e se representa por i, e normalmente aparece na forma de porcentagem

Não seria difícil compreendermos que numa aplicação financeira:

Quanto maior for o Capital, maior será o juro

Quanto maior for o tempo de aplicação, maior será o juro

Quanto maior for a taxa de aplicação, maior será o juro

Com isso, percebemos que o juro é diretamente proporcional ao Capital, à taxa e ao tempo. Como o problema só envolve grandezas
proporcionais, o cálculo do juro se faz por meio da seguinte fórmula:



Onde: j = juros ; C = Capital ; i= taxa (%) e t = tempo

Observação Importante : Para aplicação dessa fórmula precisamos ter a taxa e o tempo sob a mesma unidade de tempo.

Se a taxa for ao ano ( a.a. ) o tempo será dado em anos.
Se a taxa for ao mes ( a.m. ) o tempo será dado em meses.
Se a taxa for ao dia ( a.d. ) o tempo será dado em dias.

Montante

Chamamos Montante à soma do Capital com os juros por ele obtido:



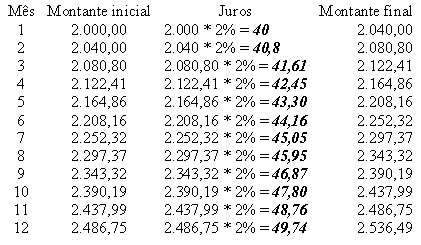
Juros Compostos: Os juros são compostos quando, no fim de cada unidade de tempo, são reunidos ao capital e o cálculo dos juros no
período seguinte é feito sobre esse novo montante. Se o capital permanece invariável, durante toda a transação os juros são simples.
Ao fim de uma unidade de tempo juros simples e juros compostos representam a mesma coisa.

Façamos um quadro comparativo entre Juros Simples e Juros Compostos. E para tal usemos o exemplo :

Sr. Junqueira investiu R$ 10 000,00 em um banco. Indique o montante após 3 meses, sabendo que o banco paga:

Quadro I) juro simples de 10% ao mês e Quadro II) juro composto de 10% ao mês;

Juros Capital Montante 1º Mês Montante 2º Mês Montante 3º Mês
Simples R$ 10.000,00 R$ 11.000,00 R$ 12.000,00 R$ 13.000,00
Compostos R$ 10.000,00 R$ 11.000,00 R$ 12.100,00 R$ 13.310,00


Quadro III) juro simples de 20% ao mês e Quadro IV) juro composto de 20% ao mês.

Juros Capital Montante 1º Mês Montante 2º Mês Montante 3º Mês
Simples R$ 10.000,00 R$ 12.000,00 R$ 14.000,00 R$ 16.000,00
Compostos R$ 10.000,00 R$ 12.000,00 R$ 14.400,00 R$ 17.280,00


Percebemos que ao término de cada unidade de tempo os Montantes de juros compostos se distanciam cada vez mais dos
Montantes de juros simples.

Juros Simples - Exercícios Resolvidos

Vamos compreender melhor o assunto Juros Simples praticando com alguns exercícios.

Exemplo 01) Calcular os juros produzidos por um capital de R$ 60.000,00 empregado à taxa de 8% a.a. ao fim de 3 anos.

Resolução : Pelo enunciado temos : C = R$ 60.000,00 ; i = 8% a.a. e t = 3 anos

Como taxa e tempo estão sob a mesma unidade de tempo, podemos aplicar a fórmula :



Se pretendêssemos calcular o Montante, este seria igual a : M = R$ 60.000,00 + R$ 14.400,00 = R$ 74.400,00.

Exemplo 02) Quais são os juros produzidos por um capital de R$ 3.000,00 num tempo de 5 anos e 4 meses à taxa de 2% ao mês?

Resolução : Pelo exposto temos : C = R$ 3.000,00 ; i = 2% a.m. e t = 5 anos e 4 meses

Transformando o tempo em meses, teremos: 5 anos e 4 meses = 5 x 12 + 4 = 64 meses e aplicando a fórmula, teremos :



Se pretendêssemos calcular o Montante, este seria igual a : M = R$ 3.000,00 + R$ 3.840,00 = R$ 6.840,00.

Exemplo 03) Calcular o montante produzido por um capital de R$ 50.000,00 empregado à taxa de 0,8% ao mês, no fim de 2 anos,
4 meses e 15 dias.

Resolução : Os dados são : C = R$ 50.000,00 ; i = 0,8 % a.m. e t = 2 anos, 4 meses e 15 dias.

Transformando o tempo em meses, teremos: 2 anos, 4 meses e 15 dias = 2 x 12 = 24 meses + 4 meses + 1/2 mês = 28,5 meses e
aplicando a fórmula, teremos :



E o Montante será : M = R$ 50.000,00 + R$ 11.400,00 = R$ 61.400,00.

Exemplo 04) Uma pessoa deseja obter uma renda mensal de R$ 1.200,00. Que capital, à taxa de 5% ao ano, deve empregar?

Resolução : Os dados são : j = R$ 1.200,00 ; i = 30 % a.a. e t = 1 mês.

Transformando o tempo em ano, teremos: 1 mês = 1/12 ano e aplicando a fórmula, teremos :



Exemplo 05) A que taxa mensal um capital de R$ 18.000,00 rende de juros em 5 anos a importância de R$ 7.200,00 ?

Resolução : Os dados são : j = R$ 7.200,00 ; C = R$ 18.000,00 e t = 5 anos.

Transformando o tempo em meses, já que a taxa é solicitada a.m., teremos: 5 anos = 60 meses e aplicando a fórmula, teremos :



Exemplo 06) Por quanto tempo é necessário deixar depositado num banco a importância de R$ 9.000,00 para obter-se R$ 5.400,00 de
juros, sabendo-se que a taxa paga por esse banco é de 4 % ao ano?

Resolução : Os dados são : j = R$ 5.400,00 ; C = R$ 9.000,00 e i = 4 % a.a. Aplicando a fórmula, teremos :



Exemplo 07) Ao fim de quanto tempo ficará triplicado um capital colocado a 2% a.m. ?

Resolução : Se o capital triplicar, então o montante é o triplo do capital, e com isso, podemos escrever :

M = C + J 3C = C + J J = 3C - C = 2C

Os dados serão : j = 2C ; C = C e i = 2 % a.m. Aplicando a fórmula, teremos :



11.15 - Exercícios Propostos

01) Calcule o juro produzido por R$ 24.000,00, durante 5 meses, a uma taxa de 6,5% ao mês.

02) Calcule o juro produzido por R$ 8.000,00, durante 5 meses, a uma taxa de 0,5% ao dia.

03) Calcule o juro produzido por R$ 4.800,00, durante 10 meses, a uma taxa de 36% ao ano.

04) Qual é o juro produzido pelo capital de R$ 18.500,00 durante 1 ano e meio, a uma taxa de 7,5% ao mês ?

05) Por quanto tempo devo aplicar R$ 10.000,00 para que renda R$ 4.000,00 a uma taxa de 5% ao mês ?

06) Em quanto tempo um capital de R$ 34.000,00, empregado a uma taxa de 10% ao ano rendeu R$ 13.600,00 de juro ?

07) A que taxa mensal devo empregar um capital de R$ 20.000,00 para que, no fim de 10 meses, renda R$ 18.000,00 de juros?

08) Qual o capital que produziu R$ 7.000,00, durante 2 anos, a uma taxa de 7 % ao ano ?

09) Calcule a que taxa foi empregado um capital de R$ 12.000,00 que produziu R$ 1.200,00 de juro, durante 2 anos.

10) Coriolano atrasou no pagamento de uma prestação de R$ 480,00 ao Sistema Financeiro de Habitação e vai ter de pagar pelo
atraso um juro de 72% ao ano. Qual é o novo valor da prestação, se o atraso foi de 30 dias ?

11) Sabendo que R$ 25.000,00 foram emprestados a uma taxa diária de 0,2%, determine o juro produzido ao final de 4 meses e 10 dias.

12) Obtive um empréstimo de R$ 58.000,00 durante 3 meses a uma taxa de 60% ao ano. Como vou pagar esse empréstimo em
5 prestações mensais e iguais, o valor de cada prestação será de:

a) R$ 11.600,00 b) R$ 13.920,00 c) R$ 13.340,00 d) R$ 13.688,00

13) ( VUNESP -SP ) Num balancete de uma empresa consta que um certo capital foi aplicado a uma taxa de 30% ao ano, durante
8 meses, rendendo juros simples no valor de R$ 192,00. O capital aplicado foi de:

a) R$ 960,00 b) R$ 288,00 c) R$ 880,00 d) R$ 2.880,00

14) ( UNIRIO - RJ ) Para comprar um tênis de R$ 70,00, Renato deu um cheque pré-datado de 30 dias no valor de R$ 74,20. A taxa de
juros cobrada foi de :

a) 6 % ao mês b) 4,2 % ao mês c) 42 % ao mês d) 60% ao mês

15) ( FSM - RJ ) João tomou R$ 200,00 a juros simples de 5 % ao mês , Um mês após o empréstimo, pagou R$ 100,00 e, um mês depois
desse pagamento, liquidou a dívida. O valor desse último pagamento foi de :

a) R$ 110,00 b) R$ 112,50 c) R$ 115,50 d) R$ 120,00

11.16 - Respostas dos Exercícios Propostos

01 R$ 7.800,00 02 R$ 6.000,00 03 R$ 1.440,00 04 R$ 24.975,00
05 8 meses 06 4 anos 07 9 % ao mês 08 R$ 50.000,00
09 5 % ao ano 10 R$ 508,80 11 R$ 2.900,00 12 letra C
13 letra A 14 letra A 15 letra D
www.matematicamuitofacil.com

Juros Simples e Compostos

No regime de juros simples as taxa de juros são aplicadas somente sobre o capital inicial. Dessa forma podemos concluir que o valor dos juros em cada mês é o mesmo. Essa forma de aplicação não é utilizada atualmente, mas serve de parâmetro para o estudo dos juros compostos. Vamos demonstrar a rentabilidade do dinheiro no regime de juros simples de acordo com o exemplo.

Vamos determinar o valor do montante de um capital de R$ 1.650,00 aplicados a uma taxa de 2% ao mês durante 12 meses.

O valor do juro mensal é de R$ 33,00. Considerando que o dinheiro ficou aplicado durante 12 meses, teremos: 12 * 33 = 396 reais de juros. O montante deverá ser calculado adicionando o capital aplicado ao valor total dos juros. Montante é igual a R$ 1 650,00 + R$ 396 = R$ 2 046,00.

A tabela foi construída no intuito de demonstrar a movimentação de uma aplicação no regime de juros simples. Sua utilização se torna inviável para o cálculo de aplicações que envolva longos períodos. Para tal situação devemos utilizar expressões matemáticas que determinam o valor dos juros e do montante de acordo com a taxa de juros e o tempo de aplicação. Observe:

J = C * i * t
M = C + J

J = juros
C = capital
i = taxa de juros
t = tempo de aplicação
M = montante

Vamos calcular o valor do montante de uma aplicação de R$ 620,00 durante 15 meses a uma taxa mensal de 1,5%, utilizando o regime de juros simples.

C = 620
i = 1,5% = 1,5/100 = 0,015
t = 15

j = 620 * 0,015 * 15
j = 139,50

M = C + J
M = 620 + 139,5
M = 759,50

O valor do montante final será de R$ 759,50.

Com a ajuda dessas expressões podemos determinar o valor dos juros, do tempo e da taxa de juros.

Calculando a taxa de juros

A que taxa de juros devemos aplicar um capital de R$ 3 500,00 que após 8 meses deve formar um montante de R$ 4 060,00.

J = 4 060 – 3500
J = 560

J = C * i * t
560 = 3500 * i * 8
560 = 28000* i
560 / 28000 = i
i = 0,02
i = 2 %
A taxa correspondente é de 2%

Calculando o tempo

Depois de quanto tempo um capital de R$ 2 230,00 gerou um montante de R$ 2 564,50 a taxa de 1,5% ao mês?

J = 2 564,50 – 2230
J = 334,5

J = C * i * t
334,5 = 2230 * 0,015 * t
334,5 = 33,45 * t
334,5 / 33,45 = t
t = 10

O tempo foi de 10 meses.
Podemos dizer que juro é uma remuneração calculada sobre um capital, uma taxa recebida por alguém que emprestou dinheiro, os lucros de um investimento financeiro, entre outras definições. Muitas pessoas realizam depósitos em bancos, pois dessa forma o investidor fornece às instituições financeiras um capital o qual ela possa investir, e por esse capital o investidor recebe uma quantia extra denominada juros. Os juros são divididos em dois: simples e compostos. Vamos dar ênfase ao estudo dos juros compostos em virtude de sua forma de capitalização ser a mais utilizada atualmente.

No regime de capitalização composta, os juros do mês são incorporados ao capital seguinte, que aplicados à taxa de juros fixa geram um novo montante a cada mês. Essa prática recebe o nome de juros sobre juros. Observe a planilha de rendimentos envolvendo juros compostos:

Considere que uma pessoa aplique R$ 1500,00 durante 8 meses em um banco que paga 1,5% de juro ao mês. Qual será o valor ao final da aplicação?

A tabela serve como suporte para visualizarmos melhor o andamento da aplicação financeira no regime de juros compostos. Mas nas situações em que o tempo de aplicação é muito extenso, utilizamos uma fórmula matemática. Veja:

M = C * (1 + i)t, onde:

M: montante
C: capital
t: tempo de aplicação
i: taxa de juros da aplicação

Exemplo 1

Um investidor aplica R$ 2 200,00 durante 12 meses a uma taxa de juros de 1% ao mês. Determine o montante produzido por essa aplicação.

M = ?
C = 2200
t = 12
i = 1% → 1 / 100 → 0,01

M = C * (1 + i)t
M = 2200 * (1 + 0,01)12
M = 2200 * 1,0112
M = 2200 * 1,126825
M = 2479,02

O montante produzido será de R$ 2 479,02.

Exemplo 2

Uma empresa toma emprestado junto a um banco a quantia de R$ 20 000,00. Essa quantia será paga após 2 anos e 6 meses a uma taxa de juros mensais de 0,75%. Qual o valor a ser pago pelo empréstimo?

M = ?
C = 20 000
t = 2 anos e 6 meses = 30 meses
i = 0,75% → 0,75/100 → 0,0075

M = C * (1 + i)t
M = 20 000 * (1 + 0,0075)30
M = 20 000 * 1,007530
M = 20 000 * 1,251272
M = 25 025,44

O valor a ser pago pelo empréstimo será de R$ 25 025,44.
www.bancodeconcursos.com

JUROS SIMPLES E COMPOSTO

JUROS SIMPLES

Quando se deposita ou empresta uma certa quantia, denominada capital por um certo tempo, recebe-se como compensação outra quantia , chamada juros.

Capital __c___ (quantia emprestada)
Taxa____ i___ (porcentagem envolvida)
Tempo___t___ (período do empréstimo)
Juros____j____(a renda obtida)


Os problemas sobre juros simples podem ser resolvidos por meio de uma regra de três composta. Na pratica são resolvidos através de formula.

Exemplo:
O capital 100 em 1 ano produz i
O capital c em t anos produzira j

Capital______tempo______juros

100_________1____________i
c___________ t____________J

I/j=100/c.1/t

i/j= 100/c.t

100j= c.i.t

j=c.i.t/100



OBESERVAÇÃO

A formula somente é válida quando a taxa e o tempo estiverem numa mesma unidade

Exemplos

Calcular os juros produzidos por um capital de R$ 5.000,00 empregado à taxa de 90% ao ano, durante 2 anos

Solução
J = ?, c = 5000, i = 90% ao ano, t = 2 anos

Temos: j = c.i.t / 100
Substituindo temos:

J = 5000.90.2 / 100
J = 900000/ 100
J = 9000

Exemplo “2”
Calcular os juros produzidos por um capital de R$ 10.000,00 empregado à taxa de 3% ao mês, durante um ano.

Temos: j = c . i . t / 100

J= 10000.3.12 / 100
J = 360000 / 100
J = 3600

Exemplo “3”

Qual o capital que, em quatro meses, rendeu R$ 11.520,00 de juros à taxa de 96% ao ano?

Temos : j = c.i.t / 100

11520 = c.8.4 / 100
32c = 1152000
c = 1152000 / 32
c = 36000

Exemplo “4”

Durante quanto tempo ficou empregado um capital de R$ 45.000,00 que rendeu R$ 8.100,00 de juros, à taxa de 2% ao mês?

Temos : j = c.i.t / 100

8100 = 45000. 2. t / 100
90000t = 810000
t = 810000 / 90000
t = 9

EXERCICIOS

1) Calcule o juro produzido por R$ 50.000,00 durante 2 anos , a taxa de 30% ao ano. (R=30.000)
2) Calcule o juro produzido por R$ 18.000,00, durante 3 meses, a taxa de 7% ao mês. (R=3780)
3) Calcule o juro produzido por R$ 72.000,00, durante 2 meses , a taxa de 60% ao ano (R=7200)
4) Calcule o juro produzido por R$ 12.000,00, durante 5 meses, a taxa de 6,5% ao mês (R= 3900)5) Por quanto tempo devo aplicar R$ 10.000,00 para que a renda R$ 4.000,00 a uma taxa de 5% ao mês? (R=8)
6) Por quanto tempo devo aplicar R$ 3.000,00 para que renda R$ 1.440,00 a taxa de 12% ao mês? (R = 4)
7) A que taxa mensal devo empregar um capital de R$ 10.000,00 para que, no fim de 2 meses renda R$ 2.000,00 de juros? (R=10%)
8) A que taxa mensal devo empregar um capital de R$ 20.000,00 para que, no fim de 10 meses renda R$ 18.000,00 de juros? (R= 9%)
9) Qual será o capital que em 9 meses, a 6% ao mês, renderá R$ 32.400,00 de juros ? (R= 60.000)10) Qual será o capital que,em 3 meses, a 72% ao ano renderá R$ 720,00 de juros? (R=4.000)
http://jmpmat4.blogspot.com/

Juros simples

Os juros simples são calculados com base no capital inicial (C), período a período. Por isso o valor dos juros simples é constante em cada período de tempo. Observe o exemplo a seguir:

Carlos aplicou R$ 500,00 a taxa de 3% no regime de juros simples. Qual será o montante no fim de 8 meses de aplicação?


Após 8 meses, Carlos terá um montante de R$ 620,00

Exemplo 2

Fernando aplicou R$ 1.200,00 em uma instituição bancária que paga juros simples de 2,5% ao mês. Qual será o montante no final de 10 meses?

O montante do juro simples e dado pela expressão: M = C + J
Fórmula para o cálculo de juros simples: J = C * i * t , em que:
J = juros
C = capital
i = taxa
t = tempo (período de aplicação)
M = montante

Dados do exercício:
J = ?
C = 1.200
i = 2,5% = 2,5/ 100 = 0,025 (taxa unitária)
t = 10 meses

Desenvolvendo
J = 1200 * 0,025 * 10
J = 300

M = 1200 + 300
M = 1500

O montante ao final de 10 meses será de R$1.500,00.

Exemplo 3

Um capital de R$ 2.000,00, aplicado no sistema de juros simples, produziu um montante de R$ 2.720,00 após 12 meses de aplicação. Qual foi a taxa de juros?
Dados:
C = 2.000
M = 2.720
J = M – C = 2720 – 2000 = 720
t = 12 meses
i = ?

J = C * i * t
720 = 2000 * 12 * i
720 = 24000 * i
i = 720/24000
i = 0,03 ou 3%

A taxa de juros usada foi de 3%.


Exemplo 4

Um capital de R$ 1.000,00, aplicado a juros simples com uma taxa de 2% ao mês, resultou no montante de R$ 1.300,00 após certo tempo. Qual o tempo da aplicação?

C = 1.000
M = 1.300
J = 1300 – 1000 = 300
i = 2% = 2/100 = 0,02
t = ?

J = C * i * t
300 = 1000 * 0,02 * t
300 = 20 * t
t = 300/20
t = 15 meses

O tempo de aplicação foi de 15 meses.

Regra de três

Professor de Matemática Antonio Carlos Carneiro Barroso

Colégio Estadual Dinah Gonçalves

email accbarroso@hotmail.com

Blog HTTP://ensinodematemtica.blogspot.com

http://accbarrosogestar.blogspot.com.br        www.youtube.com/accbarroso1

1) Uma pessoa recebe R$ 10.000 por 25 dias de trabalho. Quanto receberia se tivesse trabalhando 8 dias a mais?

a) R$ 12.300,00
b) R$ 10.400,00
c) R$ 11.300,00
d) R$ 13.100,00
e) R$ 13.200,00

2) No mesmo instante em que um prédio de 4,5m de altura projeta uma sombra de 13,5 m, qual a sombra projetada por uma torre de 130 m de altura?

a) 290m
b) 390m
c) 490m
d) 590m
e) 690m

3) A razão das idades de duas pessoas é 2/3. Achar estas idades sabendo que sua soma é 35 anos.

a) 14 e 20 anos
b) 14 e 21 anos
c) 15 e 20 anos
d) 18 e 17 anos
e) 13 e 22 anos

4) (FGV) Em 1º . 03 . 95 , um artigo que custava R$ 250,00 teve seu preço diminuído em p% do seu valor . Em 1o . 04 . 95 , o novo preço foi novamente diminuído em p% do seu valor , passando a custar R$ 211,60 . O preço desse artigo em 31. 03 . 95 era :

a) R$ 225,80
b) R$ 228,00
c) R$ 228,60
d) R$ 230,00
e) R$ 230,80

5) A razão das áreas de duas figuras é 4/7. Achar essas áreas sabendo que a soma é 66 cm².

a) 22cm² e 44cm²
b) 20cm² 46cm²
c) 21cm² e 45cm²
d) 24cm² e 42 cm²
e) 23cm² e 43cm²

6) A diferença dos volumes de dois sólidos é 9cm³ e a sua razão é 2/3. Achar os volumes.

a) 17cm³ e 28cm³
b) 18cm³ e 27cm³
c) 19cm³ e 28cm³
d) 20cm³ e 27cm³
e) n.d.a

7) Uma pessoa emprega uma quantia a juros simples de 6% durante 5 anos e o montante a juros simples de 12% ao ano durante 2 anos e recebeu R$ 80.600,00 de montante . Qual o capital inicial ?

a) R$ 50.000
b) R$ 60.000
c) R$ 70.000
d) R$ 80.000
e) R$ 90.000

8) (PUC) Em uma corrida de cavalos , o cavalo vencedor pagou aos seus apostadores R$ 9 por cada R$ 1 apostado . O rendimento de alguém que apostou no cavalo vencedor foi de:

a) 800%
b) 90%
c) 80%
d) 900%
e) 9%

9) (FEI) O custo de produção de uma peça é composta por : 30% para mão de obra , 50% para matéria prima e 20% para energia elétrica . Admitindo que haja um reajuste de 20% no preço de mão de obra , 35% no preço de matéria prima e 5% no preço da energia elétrica, o custo de produção sofrerá um reajuste de:

a) 60%
b) 160%
c) 24,5%
d) 35%
e) 4,5%

10) (UNESP) Entre 10 de fevereiro e 10 de novembro de 1990 o preço do quilograma de mercadorias num determinado "sacolão" sofreu um aumento de 275% . Se o preço do quilograma em 10de novembro era de Cr$ 67,50 , qual era o preço em 10 de fevereiro ?

a) Cr$ 19,00
b) Cr$ 18,00
c) Cr$ 18,50
d) Cr$ 19,50
e) Cr$ 17,00

11) (FUVEST) Suponha que a taxa de inflação seja 30% ao mês durante 12 meses ; daqui a um ano seja instituído o "cruzado novo ", valendo Cz$ 1000 ; e que sejam colocadas em circulação moedas de 10 centavos , 50 centavos e 1 cruzado novo . Qual será então o preço , em cruzados novos , de um cafezinho que custa hoje Cz$ 20,00 ?

a) NCZ$ 0,20
b) NCZ$ 0,30
c) NCZ$ 0,40
d) NCZ$ 0,50
e) NCZ$ 0,60

12) (FUVEST) O salário de Antônio é 90% do de Pedro . A diferença entre os salários é de R$ 500,00 . O salário de Antônio é:

a) R$ 5500,00
b) R$ 4500,00
c) R$ 4000,00
d) R$ 5000,00
e) R$ 3500,00

13) (FUVEST) Numa certa população 18% das pessoas são gordas , 30% dos homens são gordos e 10% das mulheres são gordas . Qual a porcentagem de homens na população ?

a) 30%
b) 35%
c) 40%
d) 45%
e) 50%

14) (FAAP) Numa cidade , 12% da população são estrangeiros . Sabendo-se que 11.968.000 são brasileiros , qual é a população total ?

a) 1.360.000
b) 13.600.000
c) 136.000.000
d) 10.531.840
e) 105.318.400

15) (FUVEST) O preço de uma certa mercadoria sofre anualmente um acréscimo de 100% . Supondo que o preço atual seja R$ 100,00 , daqui a 3 anos o preço será.

a) R$ 300,00
b) R$ 400,00
c) R$ 600,00
d) R$ 800,00
e) R$ 1000,00

16) (FGV) Se uma mercadoria sofre dois descontos sucessivos de 15% e depois um acréscimo de 8% , seu preço final , em relação ao preço inicial:

a) aumentou de 22%
b) decresceu de 21,97%
c) aumentou de 21,97%
d) decresceu de 23%
e) decresceu de 24%

17) (FGV) Uma fábrica de sapatos produz certo tipo de sapatos por R$ 18,00 o par , vendendo por R$ 25,00 o par . Com este preço , tem havido uma demanda de 2000 pares mensais . O fabricante pensa em elevar o preço em R$ 2,10. Com isto as vendas sofrerão uma queda de 200 pares . Com esse aumento no preço de venda seu lucro mensal:

a) cairá em 10%
b) aumentará em 20%
c) aumentará em 17%
d) cairá em 20%
e) cairá em 17%

18) (FGV) Se João emagrecesse 10 kg , ele passaria a ter 75% do seu peso atual . Então , seu peso atual é:

a) inferior a 30 kg
b) 75 kg
c) 50 kg
d) superior a 75 kg
e) 40 kg

19) (FGV) Um indivíduo ao engordar passou a ter 38% a mais em seu peso . Se tivesse engordado de tal maneira a aumentar seu peso em apenas 15%, estaria pesando 18,4 kg a menos . Qual era seu peso original ?

a) 50 kg
b) 60 kg
c) 70 kg
d) 80 kg
e) 40 kg

20) (FGV) Num colégio com 1000 alunos , 65% dos quais são do sexo masculino , todos os estudantes foram convidados a opinar sobre o novo plano econômico do governo . Apurados os resultados , verificou-se que 40% dos homens e 50% das mulheres manifestaram-se favoravelmente ao plano . A porcentagem de estudantes favoráveis ao plano vale:

a) 43,5%
b) 45%
c) 90%
d) 17,5%
e) 26%

21) (PUC) Em uma certa comunidade existem 200.000 professores de 1º e 2º graus que trabalham na rede oficial do Estado, 25.000 professores de 1º e 2º graus que trabalham na rede particular de ensino e 12.000 professores de 3º grau . Se 2,5% dos professores da rede oficial trabalham na rede particular , se 0,25% dos professores da rede oficial trabalham no 3º grau , e se 2% dos professores da rede particular trabalham no 3º grau , quantos professores possui essa comunidade , se apenas 200 professores trabalham , simultaneamente , na rede pública , particular , e no 3º grau ?

a) 213200
b) 231200
c) 212300
d) 223100
e) 231000

22) (ESPM) O salário médio de uma indústria de 354 funcionários é de R$ 3.300,00 . Se a indústria der um aumento de 20% para cada funcionário que possui , qual será o novo salário médio ?


a) R$ 3.690,00
b) R$ 369,00
c) R$ 396,00
d) R$ 3.960,00
e) n.d.a

23) (OSEC) Em apenas 6 meses o preço de um litro de gasolina teve 320% de aumento. Como esse preço era inicialmente de R$ 0,25 , ele passou a ser:

a) R$ 0,80
b) R$ 1,05
c) R$ 1,50
d) R$ 2,80
e) R$ 2,85

24) (FUVEST) Um recipiente contém uma mistura de leite natural e de leite de soja num total de 200 litros , dos quais 25% são de leite natural . Qual é a quantidade de leite de soja que deve ser acrescentada à essa mistura para que ela venha a conter 20% de leite natural ?

a) 40
b) 43
c) 48
d) 50
e) 60

25) (FGV) Duas irmãs , Ana e Lúcia , têm uma conta de poupança conjunta . Do total do saldo , Ana tem 70% e Lúcia 30% . Tendo recebido um dinheiro extra , o pai das meninas resolveu fazer um depósito exatamente igual ao saldo na caderneta . Por uma questão de justiça , no entanto , ele disse às meninas que o depósito deveria ser dividido igualmente entre as duas . Nessas condições , a participação de Ana no novo saldo:

a) diminui para 60%
b) diminuiu para 65%
c) permaneceu em 70%
d) aumentou para 80%
e) é impossível de ser calculada se não conhecermos o valor

26) (ESPM) O preço do papel sulfite , em relação ao primeiro semestre de 1989 , teve um aumento de 40% em agosto e um outro de 32% em setembro . No mês de novembro , teve um desconto de 25% . Qual seria o aumento do papel se ele fosse único?

a) 37%
b) 38,6%
c) 36,8%
d) 35,4%
e) 34,5%

27) Um automóvel com velocidade de 80 km/h demora 3h para percorrer uma certa distância.Quanto o tempo demorará para percorrer a mesma distância um outro auto cuja velocidade é de 120 km/h?

a) 2 horas
b) 3 horas
c) 4 horas
d) 5 horas
e) 6 horas

28) Uma roda de 30 dentes engrena com outra de 25 dentes. Quantas voltas dará esta última quando a primeira der 175 voltas.

a) 10 voltas
b) 110 voltas
c) 210 voltas
d) 310 voltas
e) 410 voltas

29) Para forrar as paredes de uma sala são necessárias 20 peças de papel com 80 cm de largura cada. Quantas peças seriam necessárias se as peças tivessem 1m de largura?

a) 15 peças
b) 16 peças
c) 17 peças
d) 18 peças
e) 19 peças


Porcentagem, razão e proporção
Gabarito dos exercícios
Questão 1 E
Questão 2 B
Questão 3 B
Questão 4 D
Questão 5 D
Questão 6 B
Questão 7 A
Questão 8 A
Questão 9 C
Questão 10 B
Questão 11 D
Questão 12 B
Questão 13 C
Questão 14 B
Questão 15 D
Questão 16 B
Questão 17 C
Questão 18 E
Questão 19 D
Questão 20 A
Questão 21 B
Questão 22 D
Questão 23 B
Questão 24 D
Questão 25 A
Questão 26 B
Questão 27 A
Questão 28 C
Questão 29 B

Juros Compostos

Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso

Colégio Estadual Dinah Gonçalves

email accbarroso@hotmail.com          

 www.ensinodematemtica.blogspot.com.br     www.accbarrosogestar.wordpress.com

www.accbarrosogestar.blogspot.com.br 

      

Juros Compostos

Marcos Noé

Capitalização composta

O juro composto é um regime de capitalização muito usado atualmente em razão de sua crescente rentabilidade. Nesse tipo de capitalização, o juro, a partir do segundo período, é calculado baseado no valor do montante do período anterior. Vamos através de planilhas demonstrar passo a passo a capitalização imposta por esse tipo de movimentação financeira.

Vamos supor que uma pessoa aplique o capital de R$ 2.000,00 a juros mensais de 2% ao mês durante 12 meses, no regime de capitalização composto (juros compostos). Qual o montante ao final da aplicação?

Utilizando a fórmula M = C * (1 + i)^t

C = 2000
t = 12 meses
i (taxa de juros) = 2% = 2/100 = 0,02

M = 2000 * (1 + 0,02)¹²
M = 2000 * 1,0212
M = 2000 * 1,268241794562545318301696
M = 2.536,49

Planilha da aplicação

Taxa de Juros Acumulada

Algumas situações cotidianas voltadas para a Matemática Financeira envolvem a variação dos preços de mercadorias. As variações podem ocorrer no sentido dos preços aumentarem ou diminuírem, ocorrendo, respectivamente, inflação ou deflação.
É comum em momentos de inflação o reajuste sucessivo de preços, envolvendo índices percentuais. Caso um determinado produto seja reajustado continuamente, temos a incidência de vários índices percentuais sobre o preço original. Nesse caso, dizemos que a incidência desses índices, sucessivas vezes, é chamada de taxa de juros acumulada.

A taxa de juros acumulada de determinado produto é dada pela seguinte expressão matemática:

Exemplo 1

Em razão da alta da inflação em sucessivos meses, o preço de uma mercadoria foi reajustado nos meses de janeiro, fevereiro, março e abril em 5%, 8%, 12% e 7%, respectivamente. Determine a taxa de juros acumulada desses quatro meses.

Transformando taxas percentuais em taxas unitárias:

5% = 5/100 = 0,05
8% = 8/100 = 0,08
12% = 12/100 = 0,12
7% = 7/100 = 0,07

A taxa de juros acumulada nos quatro meses foi equivalente a 35,9% ou, de forma arredondada, 36%.

Exemplo 2

Ao ser pesquisado mensalmente o preço de uma mercadoria, foram registrados os seguintes valores no último dia do mês:

Agosto: R$ 5,50
Setembro: R$ 6,20
Outubro: R$ 7,00
Novembro: R$ 7,10
Dezembro: R$ 8,90

Determine a taxa de juros acumulada referente ao aumento da mercadoria em questão.

Vamos primeiramente calcular os índices de aumento. Veja:

Taxa acumulada

A taxa acumulada dos aumentos sucessivos de preços dessa mercadoria é equivalente a 61,79% ou, de forma arredondada, 62%.

Por Marcos Noé

Regra de três composta

Regra de Três Composta

1. Uma olaria produz 1470 tijolos em 7 dias, trabalham 3 horas por dia. Quantos tijolos produzirá em 10 dias, trabalhando 8 horas por dia?

2. Oitenta pedreiros constroem 32m de muro em16 dias. Quantos pedreiros serão necessários para construir 16m de muro em 64 dia?

3. Um ônibus percorre 2232km em 6 dias, correndo 12 horas por dia. Quantos quilômetros percorrerá em 10 dias, correndo 14 horas por dia?

4. Numa fábrica, 12 operários trabalhando 8 horas por dia conseguem fazer 864 caixas de papelão. Quantas caixas serão feitas por 15 operários que trabalham 10 horas por dia?

5. Vinte máquinas, trabalhando 16 horas por dia, levam 6 dias para fazer um trabalho. Quantas máquinas serão necessárias para executar o mesmo serviço, se trabalharem 20 horas por dia, durante 12 dias?

6. Numa indústria têxtil, 8 alfaiates fazem 360 camisas em 3 dias. Quantos alfaiates são necessários para que sejam feitas 1080 camisas em 12 dias?

7. Um ciclista percorre 150km em 4 dias, pedalando 3 horas por dia. Em quantos dias faria uma viagem de 400km, pedalando 4 horas por dia?

8. Num internato, 35 alunos gastam 15.400 reais pelas refeições de 22 dias. Quanto gastariam 100 alunos pelas refeições de 83 dias neste internato ?

9. Empregaram-se 27,4kg de lã para tecer 24m de fazenda de 60cm de largura. Qual será o comprimento da fazenda que se poderia tecer com 3,425 toneladas de lã para se obter uma largura de 90cm?

10.Os 2/5 de um trabalho foram feitos em 10 dias por 24 operários, que trabalham 7 horas por dia. Em quantos dias se poderá terminar esse trabalho, sabendo que foram licenciados 4 operários e que se trabalham agora 6 horas por dias?

11.O consumo de 12 lâmpadas iguais, acesas durante 5 horas por dia, em 39 dias, é de 26 quilowatts. Conservando apenas 9 dessas lâmpadas acesas durante 4 horas por dia, de quanto será o consumo em 30 dias?

12.Se 15kg de papel correspondem a 3.000 folhas de 20cm de largura por 30cm de comprimento, a quantas folhas de 15cm por 20cm corresponderão 7kg de papel?
13.São necessários 1064 quilos de feno para alimentar 14 cavalos, durante 12 dias. Que quantidade de feno seria preciso para a alimentação de 6 cavalos, durante 60 dias?

14.30 operários gastam 15 dias de 8 horas para construir 52m de muro. Quantos dias de 9 horas gastarão 25 operários, para construir 39m de um muro igual?

15.6 operários, em 15 dias, fizeram a metade de um trabalho de que foram encarregados. Ao fim desse tempo, 4 operários abandonaram o serviço. Em quanto tempo os operários restantes poderão terminar o trabalho?

16.Uma frota de caminhões percorreu 3000km para transportar uma mercadoria, fazendo uma média de 60km por hora, e gastou 6 dias. Quantos dias serão necessários para, nas mesmas condições, essa mesma frota fazer 4500km com uma velocidade média de 50km por hora?

17.A produção de 400 hectares onde trabalham 50 homens sustenta 5 famílias. Quantas famílias poderão ser sustentadas, nas mesmas condições, com 600 hectares e 60 homens trabalhando?

18.Se 16 homens gastam 10 dias montando 32 máquinas, o número de dias que 20 homens necessitarão para montar 60 máquinas é:

19.Um veículo percorre uma certa distância trafegando com data velocidade constante, durante 3 horas. Quanto tempo ele gastaria para percorrer 2/3 daquela distância numa velocidade constante que fosse 3/5 da anterior?

20.Uma obra foi concluída em 60 dias usando-se 5 pedreiros e 10 aprendizes. Sabendo-se que o trabalho de dois aprendizes equivale ao de um pedreiro, quantos dias seriam necessários para concluir a mesma obra se dispuséssemos de 6 pedreiros e 12 aprendizes?

RESPOSTAS


1) 5600
2) 10
3) 4340
4) 1350
5) 8
6) 6
7) 8
8) 166.000
9) 200 cm
10) 23 dias
11) 13 KW
12) 2800
13) 2280 kg
14) 12 dias
15) 45 dias
16) 54/5 dias
17) 9
18) 15
19) 3h 20 min
20) 50

Porcentagem

Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso

Colégio Estadual Dinah Gonçalves

email accbarroso@hotmail.com

 www.ensinodematemtica.blogspot.com.br

www.accbarrosogestar.blogspot.com.br 

www.youtube.com/accbarroso1      


Percentagem? Ora, isto todo mundo sabe!!!

Bem, o mais correto é dizer que todo o mundo ouviu falar sobre percentagens. Nossa experiência é que esse é um assunto onde a grande maioria das pessoas, de alunos a até mesmo muito professor, fazem erros grosseiros e usam métodos super-complicados para resolverem os mais simples problemas.

Essa deficiência é indesculpável na medida em que o cálculo de percentagens, muito provavelmente, é o assunto matemático mais útil que se estuda na Escola. É objetivo deste texto ajudar a sanar essa deficiência.


Significado do sinal de percentagem: %

O sinal % é uma mera abreviação da expressão dividido por 100. De modo que, 800 % é a mesma coisa que 800/100, ou seja é o mesmo que que 8 por 1. Ou seja, é a mesma coisa dizermos: 800 % ou 800 por 100, ou 80 por 10, ou 8 por 1, etc.


O cálculo de percentagens compostas ou concatenadas

Estamos falando de situações como a seguinte:

Se a inflação de novembro foi 3% e a de dezembro foi 5%, qual a inflação dos dois meses?

A enorme maioria das pessoas acha que esse tipo de problema resolve-se por soma. Isso é totalmente errado. Problemas deste tipo são resolvidos por multiplicação.Vejamos:

Se no início de novembro, um produto custava p reais, no início de dezembro ele custará p reais mais 3% de p, ou seja, custará p' = p + 0,03 p = 1,03 p.

O novo preço p' terá subido, no início de janeiro, para:

p''= 1,05 p' = 1,05 x 1,03 p = 1,0815 p .

Conseqüentemente, a inflação total foi de 8,15 %.

É simplesmente fundamental que V. entenda isso. Para tal, faça os seguintes problemas, de ordem crescente de dificuldade:


EXERCÍCIO 1

Maria e José ficaram janeiro e fevereiro na praia. Maria engordou 10% em jan e 20% em fev, já José engordou 20% em jan e 10% em fev. Quem engordou mais?

RESPOSTA: sabendo que podemos fazer o produto de dois números em qualquer ordem, sem alterar o resultado, é desnecessário fazer qualquer conta para ver que os dois engordaram o mesmo percentual .


EXERCÍCIO 2

Se nossa Maria tivesse engordado 10% em jan, mas emagrecido 10% em fev, qual o efeito total?

RESPOSTA: pelo que já vimos, espero que V. tenha saído da vala comum da imensa maioria dos vestibulandos, os quais acham que o efeito total é zero ( pois 10 - 10 = 0 ). Claro que não é, pois 1,10 x 0,90 não é 1, mas 0,99 ( ie, Maria emagreceu 1%)


EXERCICIO 3

Se uma caderneta de poupança rende 0,5% ao mês, uma aplicação de 300 reais terá que saldo após 8 meses?

RESPOSTA: V. já sabe que o juro pago não é 8 x 0,5 = 4 % e que então o saldo não é 1,04 x 300 , mas sim :

1,0058 x 300 = 1,040707 x 300 = 312,21


EXERCICIO 4

No custo industrial de um livro, 60% é devido ao papel e 40% a impressão. Sendo que num ano o papel aumentou 259% e a impressão 325%, qual o aumento percentual no custo do livro?

RESPOSTA: 285,4 %


EXERCICIO 5 ( muito importante )

A incidência da malária vinha dobrando a cada 2 anos. Qual o aumento percentual anual equivalente?

RESPOSTA: Indicando por x o percentual procurado, pelo visto acima, em dois anos, o número de malarientos passa de M para

M' = ( 1 + x )2 M = 2 M

Tudo o que lhe resta fazer é resolver para x = 0,41 = 41% , aproximadamente.



Aumentos e diminuições percentuais

A rigor já trabalhamos com isso acima, no exercício 2. Examinemos novamente a idéia envolvida, usando exemplo:

Se as vendas de uma empresa aumentaram 20%, então elas passaram de v para v + 0,20 v = 1,20 v.

Se as vendas de uma empresa diminuiram 20%, então elas passaram de v para v - 0,20 v = 0,80 v.


EXERCICIO 6

Se o lucro mensal de uma empresa aumentar e diminuir, alternadamente, 10% ao mês, mostre que no final de um ano o lucro estará em 94% do lucro no início do ano. Consequentemente, terá havido uma diminuição anual de 6%.


EXERCICIO 7

A ocorrência do ciclo verão-inverno, ao contrário do que acha a vasta maioria das pessoas, não é governada pela menor ou maior proximidade da Terra em relação ao Sol, mas pela inclinação do eixo de rotação da Terra.

Contudo, pode-se observar que o verão do hemisfério-sul ( HS ) é mais quente do que o verão do hemisfério-norte ( HN ). Para isso aponta-se duas causas:

a distância Terra ao Sol no verão do HS é 4 % menor do que a correspondente distância no verão do HN .

o HS tem mais oceanos

Pede-se: levando em conta apenas a primeira dessas causas, calcular em quantos percentos o verão do HS é mais quente do que o verão do HN.

( NOTA: a partir de perguntas de vários de nossos visitantes, informamos que não está faltando nenhum dado numérico para se resolver este problema! Por outro lado, por "mais quente" queremos dizer "recebe mais energia calorífica" )

RESPOSTA: 8.5 %


Pontos percentuais

A noção de "pontos percentuais", atualmente, é bastante empregada nos meios de comunicação de massa e pelos economistas brasileiros. Seu significado pode ser facilmente entendido a partir de alguns exemplos:

se a inflação subiu de 5% para 10%, podemos tanto dizer que houve um aumento de 100% na inflação como dizer que a inflação subiu cinco pontos percentuais

se o imposto XYZ subiu de 2% para 3%, é a mesma coisa dizer que o aumento foi de 50% e dizer que o imposto subiu um ponto percentual

se a taxa de juros passou de 20% para 50%, esse aumento pode ser descrito como sendo um aumento de 150% ou como sendo um aumento de trinta pontos percentuais.


Exercícios suplementares

EXERCICIO 9

A produção de uma fábrica aumentou de 240 para 312 unidades. Consequentemente, houve um aumento de 30% na produtividade. Pergunta-se:

porque está errado dizer que a produtividade antiga era 70% da atual?

o erro apontado acima é maior quando o aumento de produtividade for um percentual grande ou quando for um percentual pequeno? Por quê?


EXERCICIO 10

Os honorários de uma agência de propaganda são compostos de duas parcelas: o custo de produção ( artistas, filmes, etc ) e uma comissão de 15% sobre o custo de produção. Por sua vez o IR ( Imposto de Renda ) cobra, da agência, um imposto que:

era de 5% do valor da comissão

passou a ser 5% do valor da comissão e mais 5% dos honorários

Pergunta-se:

Que percentual da comissão o IR representava? E agora?

O novo lucro é que percentual do antigo? Isso justifica a gritaria das agências?

RESPOSTAS: 5%, 43.3%, 59.7%


EXERCICIO 11

Na beirada de um jardim circular, foi feita uma calçada circular que aumentou a área do mesmo em 96%. Sendo que a calçada tem 4 metros de largura, pede-se o raio do jardim original.

RESPOSTA = 10 m


EXERCICIO 12

Explique por que o seguinte método funciona se, num restaurante, V. quiser acrescentar uma gorjeta de 15% à despesa D:

Primeiro escrevo o valor D e então movo a virgula decimal de D uma casa para a esquerda e escrevo essa quantidade sobre D. Finalmente, divido essa última quantidade por 2 e escrevo o resultado dessa divisão. O total a pagar é a soma das 3 quantias escritas.


EXERCICIO 13

Um quadrado tem 400 cm2 de área. De qual percentual devemos diminuir seu lado para que a área diminua 20% ?

RESPOSTA: aprox 10.56%


EXERCICIO 14

O último censo do município XYZ mostrou que no mesmo:

as mulheres representam 55% da população adulta

os homens adultos com no máximo escola primária completa representam 80% da população adulta

as mulheres adultas com no máximo escola primária completa representam 90% da população adulta

Que percentual da população adulta do município foi além da escola primária?

RESPOSTA: 14.5%
www.colaweb.com.br

Juros Simples e Compostos

Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso

Colégio Estadual Dinah Gonçalves

email accbarroso@hotmail.com          

 www.ensinodematemtica.blogspot.com.br  www.accbarrosogestar.wordpress.com

www.accbarrosogestar.blogspot.com.br 

       

Juros Simples e Compostos

Thiago Ribeiro

Juros

Cansado de Pagar Juros? Entenda os Cálculos de Juros

Quem nunca ouviu falar do tal dos Juros? Ou das taxas de juros fixadas pelo Copom (Banco Central do Brasil), taxas selic e etc?
Primeiramente, passamos o que é juros: Juros é um atributo de uma aplicação financeira, ou seja, referimos a uma quantia em dinheiro que deve ser paga por um devedor (o que pede emprestado), pela utilização de dinheiro de um credor (aquele que empresta).
Existem dois tipos de juros:
Os Juros Simples - São acréscimos que são somados ao capital inicial no final da aplicação
Juros Compostos - São acréscimos que são somados ao capital, ao fim de cada período de aplicação, formando com esta soma um novo capital.
Capital é o valor que é financiado, seja na compra de produtos ou empréstimos em dinheiro.
A grande diferença dos juros é que no final das contas quem financia por juros simples obtem um montante (valor total a pagar) inferior ao que financia por juros compostos.
A fórmula do Juro Simples é: j = C. i. t
Onde:
j = juros, C = capital, i = taxa, t = tempo.
Considerando que uma pessoa empresta a outra a quantia de R$ 2.000,00, a juros simples, pelo prazo de 3 meses, à taxa de 3% ao mês. Quanto deverá ser pago de juros?
Antes de iniciarmos a resolução deste problema, devemos descobrir, o que é o que, ou seja, quais dados fazem parte das contas.
Capital Aplicado (C) : R$ 2.000,00
Tempo de Aplicação (t) : R$ 3 meses
Taxa (i): 3% ou 0,03 ao mês (a.m.)
Fazendo o cálculo, teremos:
J = c . i. t → J = 2.000 x 3 x 0,03 → R$ 180,00
Ao final do empréstimo, a pessoa pagará R$ 180,00 de juros.
Observe, que se fizermos a conta mês a mês, o valor dos juros será de R$ 60,00 por mês e esse valor será somado mês a mês, nunca mudará.
t
A fórmula dos Juros Compostos é: M = C. (1 + i)
Onde:
M = Montante, C = Capital, i = taxa de juros, t = tempo.
Considerando o mesmo problema anterior, da pessoa que emprestou R$ 2.000,00 a uma taxa de 3% (0,03) durante 3 meses, em juros simples, teremos:
Capital Aplicado (C) = R$ 2.000,00
Tempo de Aplicação (t) = 3 meses
Taxa de Aplicação (i) = 0,03 (3% ao mês)
Fazendo os cálculos, teremos:
M = 2.000 . ( 1 + 0,03)³ → M = 2.000 . (1,03)³ → M = R$ 2.185,45
Ao final do empréstimo, a pessoa pagará R$ 185,45 de juros.
Observe, que se fizermos a conta mês a mês, no primeiro mês ela pagará R$ 60,00, no segundo mês ela pagará R$ 61,80 e no terceiro mês ela pagará R$ 63,65.
Normalmente quando fazemos uma compra nas "Casas Bahia", por exemplo, os Juros cobrados são os Juros Compostos, praticamente todas lojas comerciais adotam os Juros sobre Juros (Juros Compostos).

Juros Simples e Juros Compostos

Vimos no primeiro texto sobre Juros Simples que a fórmula clássica para o cálculo de juro simples é:

j = C x r / 100,

sendo

C = Capital
r = a taxa percentual.

Agora vamos tratar do tempo.

Se alguém empresta dinheiro a 3%a.m., isto significa por convenção (combinação, acordo, trato entre pessoas) que para cada R$ 100,00 embutidos no valor do empréstimo, R$ 3,00 deverão ser pagos como aluguel desse dinheiro todo o mês.

‘a.m.’, então, é uma combinação (convenção) entre pessoas, que quer dizer ‘ao mês’, ‘todo mês’, ‘por mês’.
Poderia ser ‘a.a.’, que significaria ‘ao ano’, ‘por ano’.
Então, simplesmente – caso seja uma taxa ‘a.m.’ – a gente multiplica o que se ganha de juro pelo tempo em meses que o dinheiro ficou à disposição de quem o tomou. Logo, o juro que sai de

j = r x C / 100

vai se repetir ‘t’ meses e a fórmula é simplesmente afetada disto, passando a ser

j = r x C / 100 x t

ou

j = Cit/100 (como nos livros).

Se o tomador permanecer 3 meses com o dinheiro do empréstimo, terá de pagar 3 x j, ou seja, r x C / 100 x 3, que pode se entendido que ele pagará três vezes mais juros do que alguém que ficaria apenas um período.

Mas vamos tratar de ‘t’ valendo 1 mês para construirmos nossa história. Assim, ainda não precisamos escrevê-lo na fórmula. Vamos entender que o ‘contrato’ é de um período apenas. Pode ser o empréstimo por apenas um mês.

A Caderneta de Poupança, por exemplo, paga 6%a.a. ao depositante (veja que o depositante aqui é quem empresta dinheiro ao banco).

Mas as sutilezas, com o desenvolvimento das relações comerciais, vão se refinando.
Uma pergunta: No caso da Caderneta de Poupança, isto significa que quem depositar seu dinheiro lá irá receber R$ 6,00 por cada R$ 100,00 somente quando seu depósito fizer um ano?
Nada impediria que fosse assim. Quem quiser emprestar dinheiro e pôr a mão nos juros após um ano de empréstimo pode fazer isto.

Mas, combinou-se outra coisa: a Caderneta de Poupança iria pagar todo mês.

Mas aí vem uma pergunta: como isso? Se eu tenho um contrato com a Caixa Econômica de receber 6% ao ano, como é que ela vai pagar ao mês?
É assim mesmo, pois entra aí uma outra coisa nova: o regime de capitalização.

O que é isto? Nada de mais, apenas quer dizer que, embora o contrato diga que os juros serão pagos ao depositante à taxa de 6%a.a. (R$ 6,00 de juros a cada ano para R$ 100,00 depositados), combinou-se que o cálculo será feito à taxa equivalente a cada mês de decurso do empréstimo, pelo tempo em meses combinado entre as partes em que estiver valendo a operação.

O regime de capitalização, no nosso exemplo, é mensal. Equivale a dizer ‘todo mês faça o cálculo do juro’.

Então, o equivalente a um mês de uma taxa de 6%a.a. é 6a.a./12, ou seja, 0,5%a.m.

A taxa de 6%a.a. então é dita ‘taxa nominal’, pois é uma taxa só de nome. Ela, integralmente, não serve ao cálculo efetivo de juro. E esta divisão por 12 é uma convenção também. Poderia ser feita de outro jeito, mas combinou-se assim. Uma divisão simples.

Por conseqüência, a verdadeira taxa da Caderneta de Poupança é 0,5%a.m. e é esta que deve ser incluída no cálculo.

Então, o juro da Caderneta de Poupança deve ser calculado – como todo juro -conforme a fórmula clássica:

j = 0,5 x C / 100.

Então vamos fazer continhas. Vamos supor alguém deposite R$ 500,00 na Caderneta de Poupança no primeiro dia útil do ano, só para facilitar tudo.

02/01/2006 -> R$ 500,00.

Quando chegar no dia 02/02/2006, há a contagem do juro:

j = 0,5 x 509,00 / 100 = R$ 2,50.

Então, a Caixa Econômica Federal deposita os R$ 2,50 na conta do depositante como aluguel do dinheiro. Esta conta-poupança fica, então, com o valor de R$ 502,50.
Este valor, por convenção (combinação entre as pessoas) passa a se chamar Montante.

Montante é o que havia antes do juros, mais os juros.

Mas aí, nosso depositante, que é uma pessoa muito influenciável, ouve falar que um outro banco paga uma taxa melhor na Caderneta de Poupança, sem saber que o sistema é unificado e as Cadernetas de Poupança obedecem sempre à regra da Caixa Econômica Federal, e saca totalmente o valor do montante. E leva para outro banco o valor total de R$ 502,50, abrindo uma nova conta.

Então, neste novo banco, ele deposita, no mesmo dia 2/2 o seu dinheiro para uma nova aplicação.

02/02/2006 -> R$ 502,50.

No dia 02/03/2006, um mês após, o novo banco paga-lhe a taxa padrão, isto é,

j = 0,5 x 502,50 / 100 = R$ 2,5125.

Como não temos representação além da dos centavos, o banco deposita R$ 2,51 em sua conta, agora somando os R$ 502,50 iniciais com os novos juros, isto é, indo o Montante para R$ 505,01.

Não satisfeito com o juro pago, ele retira o dinheiro deste banco e vai a outra Caderneta de Poupança com a mesma ilusão de ganhar mais do que antes e abre uma nova conta.

02/03/2006 -> R$ 505,01.

No dia 02/04/2006 ele vai ao banco e encontra o juro de

j = 0,5 x 505,01 / 100 = R$ 2,52,

perfazendo o montante de R$ 507,53.

Nosso amigo então percebe que perdeu tempo, teve trabalho de abrir contas desnecessariamente. Se ele tivesse deixado o dinheiro no primeiro banco, o valor seria o mesmo, pois as regras de cálculos são as mesmas e foram aplicadas sempre sobre o valor que teriam caso ficassem numa mesma instituição bancária.

Agora vamos ver o que aconteceria, caso nosso ambicioso depositante deixasse seu dinheiro na primeira conta, sem abrir todas aquelas outras.

500,00.
1o. Juro -> 0,5 x 500,00 / 100 = 2,50.

500,00 + 2,50 = 502,50.
2o. Juro -> 0,5 x 502,50 / 100 = 2,51.

502,50 + 2,51 = R$ 505,01
3o. Juro -> 0,5 x 505,01 / 100 = 2,52.
505,01 + 2,52 = 507,53.

Para prosseguir, relembremos que

Montante (M) é igual ao Capital ( C ) acrescido dos juros (j) no fim do período.

M = C + j

M = C + r x C / 100

Para facilitar, vamos dizer que não seja C o numerador daquela fraça, mas ‘r’. Reescrevamos e não mudemos nada

M = C + r / 100 x C

Para facilitar a visualização, uma vez que a divisão é por uma constante, que tal escondê-la, sem deixar de considerá-la?

Vamos trocar a alíquota ‘r’ por ‘i’, significando r/100.

M = C + i x C

Ou

M = C + Ci

ou

M = C ( 1 + i ) —> (1)

Então, se formos calcular o montante de R$ 500,00 aplicados por 1 mês, à taxa de 0,5%a.m., faríamos assim

r = 0,5; i=0,005

M = 500 ( 1 + 0,005) ou

M = 500 ( 1,005).

Aquele ’1′ do ’1 + 0,005′ representa o valor aplicado anterior.

Veja que realmente esta última fórmula dá o primeiro valor calculado ao fim do primeiro mês.

R$ 502,50.

Voltemos a (1)

M = C ( 1 + i )

Isto daria o primeiro montante.

Mas, lembra?, o primeiro montante é o ‘capital’ da segunda aplicação:

M2 = ‘M’ vezes a partícula que afeta o valor aplicado.

Releia:

M2 = { C ( 1 + i ) } x (1 + i )

Veja, (1 + i) está sendo multiplicado por si mesmo, ou seja

M2 = C ( 1 + i ) ^ 2.

Continuando,

M3 = ‘M2′ vezes a partícula que afeta o valor aplicado.

Reescrevendo M3,

M3 = { C ( 1 + i ) ^2 } x ( 1 + i)

que você pode simplificar para

M3 = C ( 1 + i ) ^ 3.

Se formos ver a aplicação inicial de R$ 500,00 no início de nossa história, teremos que

M3 = 500,00 x ( 1 + 0,005 ) ^ 3

que resulta

R$ 507,53.

Você viu que, na nossa história de alguém depositar um valor inicial e retirar após o primeiro período esse valor mais seus juros, abrir uma nova conta com o montante arrecadado e fazer uma nova aplicação para repetir isto mais à frente, resultou em cálculos isolados de juros simples.

Entretanto, o valor final, utilizando-se o recurso do cálculo de Juros Compostos levou ao mesmo resultado.

Isto funcionou em ambos os casos em virtude da taxa de aplicação (no caso, 0,5% a.m.) ser a mesma, e o valor inicial também o mesmo.

Por fim, juros compostos tratam de montantes (valor mais aluguel do valor). Ou sejam, juros simples reaplicados a cada período.

Juros Compostos

Juros compostos são muito usados no comércio, como por exemplo, nos bancos. Os juros compostos são utilizados na remuneração das cadernetas de poupança, pois oferecem uma melhor remuneração. Popularmente o juro composto é conhecido como “juro sobre juro”.
Problema de juro composto
Fernando empresta o capital inicial de R$ 4000,00 (quatro mil reais) para Pedro cobrando juros compostos de 4% ao mês. Pedro prometeu pagar tudo após 5 meses. Qual será o valor que ele terá que pagar?
Para resolvermos esse problema de juros compostos podemos usar a seguinte fórmula:
M = C * (1 + i)t
M = Montante
C = Capital Inicial
i = Taxa de juros
t = Tempo
Usando a fórmula para o problema de juro composto acima teremos:
M = ? (é o valor que queremos saber)
C = R$ 4000,00
i = 4% /100 = 0,04
t = 5
M = 4000 * (1 + 0,04)5
M= 4000 * (1,04)5
M= 4000 * 1,2165
M= 4866
Subtraindo o capital inicial do montante temos:
J = 4866 – 4000 = 866
Portanto, Pedro terá que devolver o valor de R$ 4866 (quatro mil, oitocentos e sessenta e seis reais) para Fernando. Sendo R$ 866 de juros.
Para efeito de comparação, vamos ver qual seria o valor a pagar se esses 4% fossem juros simples. O capital inicial e o tempo continua o mesmo.
J = C * i * t
J = 4000 * 0,04 * 5
J = 800
M = C + j
M = 4000 + 800
M = 4800
Se fosse juros simples o valor a ser pago seria de R$ 4800. A diferença entre o juro composto e o simples nesse caso foi de R$ 66.
Caso tenha ficado alguma dúvida sobre como calcular juros compostos basta usar o formulário de comentários logo abaixo.
Antonio Carlos Carneiro Barroso
HTTP://ensinodematemtica.blogspot.com.br

Proporção

Definimos proporção como a igualdade entre duas razões. Observe:

Dizemos que a está para b assim como c está para d. Em qualquer proporção temos que a multiplicação dos elementos dos extremos é igual à multiplicação dos elementos dos meios: a * d = c * d. Essa propriedade é considerada a fundamental das proporções.

Para verificarmos se duas razões são proporcionais, basta aplicarmos essa condição e verificarmos se o resultado é igual, caso seja, dizemos que elas são proporcionais. Vamos verificar essa regra:

Em certas situações, a propriedade fundamental das proporções deverá ser usada com o auxilio de equações na determinação da incógnita. Acompanhe alguns exemplos resolvidos:

Exemplo 1

6*(x+3) = 4*12
6x + 18 = 48
6x = 48 – 18
6x = 30
x = 30/6
x = 5

Exemplo 2

10*(2x+10) = 6*(2x-2)
20x + 100 = 12x – 12
20x-12x = -12-100
8x = -112
x = -112/8
x = -14

Exemplo 3

4*(5x-1) = 3*(x+2)
20x-4 = 3x + 6
20x – 3x = 6 + 4
17x = 10
x = 10/17

As propriedades envolvendo proporções são aplicadas à resolução de problemas ligados a regras de três diretamente e inversamente proporcionais.

Porcentagem

Utilizamos o calculo de porcentagem constantemente no nosso cotidiano .toda fração de denominador 100, representa uma porcentagem, como diz o próprio nome por cem.

Exemplo:

12/100 é igual a 0,12 que multiplicado por 100 será igual a 12%

5/100 é igual a 0,05 que multiplicado por 100 será igual a 5%


Observe que o símbolo % que aparece nos exemplos acima significa por cento.
Se repararmos em nosso volta, vamos perceber que este símbolo % aparece com muita freqüência em jornais, revistas, televisão e anúncios de liquidação, etc.

Exemplos:

O crescimento no número de matricula no ensino fundamental foi de 24%.
A taxa de desemprego no Brasil cresceu 12% neste ano.
Desconto de 25% nas compras à vista.

Devemos lembrar que a porcentagem também pode ser representada na forma de números decimal, observe os exemplos.

Exemplos:

25%/100 será igual a 0,25
7%/100 será igual a 0,07

Exemplos:

1.Uma televisão custa 300 reais. Pagando à vista você ganha um desconto de 10%. Quanto pagarei se comprar esta televisão à vista?
300 .10 = 3000 este resultado divido por 100 será igual a 30 reais

sendo assim

300 – 30 = 270
Logo, pagarei 270 reais


EXERCÍCIOS

1) Escreva as razões na forma de taxa porcentual

a) 1/100 = 7%
b) 9/100 = 9%
c) 35/100 = 35%
d) 100/100 = 100%
e) 143/100 = 143 %

2) escreva na forma de razões centesimais

a) 3% = 3/100
b) 8% = 8/100
c) 34% = 34 /100
d) 52% = 52 / 100
e) 89% = 89 /100

3) Escreva as razões forma de taxa porcentual:

a) 1/4 = 25%
b) 3/5 = 60%
c) 7/10 = 70%
d) 1/50 = 2%
e) 9/25 = 36%
f) 17/10 = 170%
g) 7/2 =350%
h) 5/4 = 125%
i) 3/8 = 37,5%

4) calcule a porcentagens:

a) 8% de R$ 700,00 = R$ 56,00
b) 5% de R$ 4.000,00 = R$ 200,00
c) 12% de R$ 5.000,00 = R$ 600,00
d) 15% de R$ 2.600,00 = R$ 390,00
e) 100% de R$ 4.520,00 = R$ 4.520,00
f) 125% de R$ 8.000,00 = R$ 10.000,00
g) 3% de 400 = 12
h) 18% de 8600 = 1.548
i) 35% de 42.000 = 14.700
j) 1% de 3000 = 30
l) 120% de 6.200 = 7.440


PROBLEMAS DE PORCENTAGEM
São resolvidos atraés de regra de três simples

exemplo 1

calcular 20% de R$ 700,00

700--------100
X-----------20

100X = 700 . 20

100x = 14000

x = 14000/100

x= 140

resposta : R$ 140,00


MÉTODO PRÁTICO

Exemplo 1

Neste caso, podemos resolver mais rapidamente, lembrando o conceito de fração:

Calcular 20% de R$ 700,00

solução:

20 / 100 . 700 =

20 . 700 / 100 = 14000/ 100 = 140

Resposta : R$ 140,00


Exemplo 2

Numa classe de 40 alunos, 36 foram aprovados. Qual a taxa de porcentagem dos aprovados?

solução:

40-------36

100------x


40/100 = 36/x

40x = 3600

x = 3600/40

x = 90

Resposta: A aprovação foi de 90%

Exemplo 3

Comprei uma camisa e obtive um desconto de R$ 12,00 que corresponde à taxa de 5%. Qual é o preço da camisa?

100/x = 5/12

5x = 1200

x = 1200 / 5

x = 240

Resposta: A camisa custava R$ 240,00


1) Numa escola de 900 alunos, 42% são rapazes. Calcule o número de rapazes. (R:378)

2) Sobre um ordenado de R$ 380,00 são descontados 8% para o INSS. De quanto é o total de descontos ? (R: 30,40)

3) Comprei uma bicicleta por R$ 500,00, Revendi com um lucro de 15%. Quanto ganhei? (R: 75,00)
4) Uma caneta que custava R$60,00 sofreu um desconto de 5%. Quanto você pagará por essa caneta? (R: R$ 57,00)
5) Por quanto deverei vender um objeto que me custou R$ 720,00 para lucrar 30% ( R: 936,00)
6) Seu pai comprou um rádio por R$ 85,00 e obteve um desconto de 12% . Quanto pagou pelo rádio? (R: 74,80)

7) Um cormeciante comprou uma mercadoria por R$ 9.500,00. Querendo obter um lucro de 12% por que preço deverá vender a mesma? ( 10.640,00)

8) Ao ser pago com atraso, uma prestação de R$ 1.300,00 sofreu um acréscimo de 4% . Qual o valor dessa prestação? (R: 1.352,00)

9) Numa classe de 40 alunos, 6 foram reprovados. Qual a taxa de porcentagem dos alunos reprovados? ( R: 15%)

10) Um feirante observou que, em cada 75 laranjas, 6 estavam estragadas. Qual a taxa de porcentagem das frutas estragadas? (R: 8%)

11) Comprei um objeto por R$ 23.000,00 e revendi com um lucro de R$ 1.610,00. Qual foi a taxa de lucro? (R: 7%)

12) Um comerciante recebeu um desconto de R$ 1.312,00 numa compra cujo valor era de R$ 82.000,00. Calcule a taxa dedesconto? (R: 1,6%)

13) Um produto custa R$ 400,00 e é vendido por R$ 520,00. Qual é a taxa de lucro? ( R: 30%)

14) Numa turma de 30 operários faltaram 12. Qual a taxa de operários presentes? (R:60%)

15) Numa classe foram reprovados 15% dos alunos, isto é , 9 alunso. Quantos alunos havia na classe? (R: 60)

16) Meu irmão ganhava R$ 320,00. Seu patrão lhe deu um aumento de 42%. Quanto ganha atualmente? (R: 454,40)

17) Num exame supletivo compareceram 12.600 candidatos e apenas 5% foram aprovados. Quantos candidatos foram aprovados? ( R: 630)

18) De 400 operários, 120 faltaram ao serviço. Qual a taxa de porcentagem dos operários, quantos são casados? (R: 30%)

19) Um produto custa R$ 600,00 e é vendido por R$ 750,00. Qual é a taxa de lucro nesse produto? (R: 25%)

20) Comprei uma vitrola por R$ 150,00 e vendi por R$ 129,00. De quanto porcento foi o prejuizo (R: 14%)

21) Um rádio foi comprado por R$ 175,00 e vendido por R$ 199,50. De quanto por cento foi o lucro? (R: 14%)



RAZÃO

Razão é a divisão ou relação entre duas grandezas

exemplos:

1) A razão de 5 para 10 é 5/10, que é igual a 1/2.

2) A razão de 10 para 5 é 10/5, que é igual a 2.

Exercícios

1) Determine a razão do primeiro para o segundo número:

a) 1 e 9 = 1/9
b) 4 e 7 = 4/7
c) 7 e 4 = 7/4
d) 25 e 11 = 25/11
e) 4 e 16 = 4/16 = 1/4
f) 16 e 4 = 16/4 = 4g) 38 e 19 = 38/19 = 2
h) 19 e 38 = 19/38 = 1/2
i) 100 e 48 = 100/48 = 25/12

PROPORÇÃO


Grandezas Proporcionais

O que estudaremos são grandezas que sejam diretamente ou inversamente proporcionais, embora existam casos em que essas relações não se observem, e que portanto, não farão parte de nosso estudo.

Por exemplo, "na partida de abertura de um campeonato, um jogador fez três gols, quantos gols ele fará ao final do campeonato sabendo que o mesmo terá 46 partidas?".

Grandezas Diretamente Proporcionais (G.D.P.)
Duas grandezas são ditas diretamente proporcionais, quando o aumento de uma implica no aumento da outra, quando a redução de uma implica na redução da outra, ou seja, o que você fizer com uma acontecerá com a outra.

Grandezas Inversamente Proporcionais (G.I.P.)
Duas grandezas são ditas inversamente proporcionais quando o aumento de uma implica na redução da outra, quando a redução de uma implica no aumento da outra, ou seja, o que você fizer com uma acontecerá o inverso com a outra.



EXERCICIOS
1) Uma pessoa recebe R$ 10.000 por 25 dias de trabalho. Quanto receberia se tivesse trabalhando 8 dias a mais?

a) R$ 12.300,00
b) R$ 10.400,00
c) R$ 11.300,00
d) R$ 13.100,00
e) R$ 13.200,00 (X)

2) No mesmo instante em que um prédio de 4,5m de altura projeta uma sombra de 13,5 m, qual a sombra projetada por uma torre de 130 m de altura?

a) 290m
b) 390m (X)
c) 490m
d) 590m
e) 690m


3) A razão das idades de duas pessoas é 2/3. Achar estas idades sabendo que sua soma é 35 anos.

a) 14 e 20 anos
b) 14 e 21 anos (B)
c) 15 e 20 anos
d) 18 e 17 anos
e) 13 e 22 anos


4) (FGV) Em 1º . 03 . 95 , um artigo que custava R$ 250,00 teve seu preço diminuído em p% do seu valor . Em 1o . 04 . 95 , o novo preço foi novamente diminuído em p% do seu valor , passando a custar R$ 211,60 . O preço desse artigo em 31. 03 . 95 era :

a) R$ 225,80
b) R$ 228,00
c) R$ 228,60
d) R$ 230,00 (D)
e) R$ 230,80


5) A razão das áreas de duas figuras é 4/7. Achar essas áreas sabendo que a soma é 66 cm².

a) 22cm² e 44cm²
b) 20cm² 46cm²
c) 21cm² e 45cm²
d) 24cm² e 42 cm² (D)
e) 23cm² e 43cm²


6) A diferença dos volumes de dois sólidos é 9cm³ e a sua razão é 2/3. Achar os volumes.

a) 17cm³ e 28cm³
b) 18cm³ e 27cm³ (B)
c) 19cm³ e 28cm³
d) 20cm³ e 27cm³
e) n.d.a


7) Uma pessoa emprega uma quantia a juros simples de 6% durante 5 anos e o montante a juros simples de 12% ao ano durante 2 anos e recebeu R$ 80.600,00 de montante . Qual o capital inicial ?

a) R$ 50.000 (A)
b) R$ 60.000
c) R$ 70.000
d) R$ 80.000
e) R$ 90.000


8) (PUC) Em uma corrida de cavalos , o cavalo vencedor pagou aos seus apostadores R$ 9 por cada R$ 1 apostado . O rendimento de alguém que apostou no cavalo vencedor foi de:

a) 800% (A)
b) 90%
c) 80%
d) 900%
e) 9%


9) (FEI) O custo de produção de uma peça é composta por : 30% para mão de obra , 50% para matéria prima e 20% para energia elétrica . Admitindo que haja um reajuste de 20% no preço de mão de obra , 35% no preço de matéria prima e 5% no preço da energia elétrica, o custo de produção sofrerá um reajuste de:

a) 60%
b) 160%
c) 24,5% (C)
d) 35%
e) 4,5%


10) (UNESP) Entre 10 de fevereiro e 10 de novembro de 1990 o preço do quilograma de mercadorias num determinado "sacolão" sofreu um aumento de 275% . Se o preço do quilograma em 10de novembro era de Cr$ 67,50 , qual era o preço em 10 de fevereiro ?

a) Cr$ 19,00
b) Cr$ 18,00 (X)
c) Cr$ 18,50
d) Cr$ 19,50
e) Cr$ 17,00


11) (FUVEST) Suponha que a taxa de inflação seja 30% ao mês durante 12 meses ; daqui a um ano seja instituído o "cruzado novo ", valendo Cz$ 1000 ; e que sejam colocadas em circulação moedas de 10 centavos , 50 centavos e 1 cruzado novo . Qual será então o preço , em cruzados novos , de um cafezinho que custa hoje Cz$ 20,00 ?

a) NCZ$ 0,20
b) NCZ$ 0,30
c) NCZ$ 0,40
d) NCZ$ 0,50 (X)
e) NCZ$ 0,60


12) (FUVEST) O salário de Antônio é 90% do de Pedro . A diferença entre os salários é de R$ 500,00 . O salário de Antônio é:

a) R$ 5500,00
b) R$ 4500,00 (X)
c) R$ 4000,00
d) R$ 5000,00
e) R$ 3500,00


13) (FUVEST) Numa certa população 18% das pessoas são gordas , 30% dos homens são gordos e 10% das mulheres são gordas . Qual a porcentagem de homens na população ?

a) 30%
b) 35%
c) 40% (X)
d) 45%
e) 50%


14) (FAAP) Numa cidade , 12% da população são estrangeiros . Sabendo-se que 11.968.000 são brasileiros , qual é a população total ?

a) 1.360.000
b) 13.600.000 (X)
c) 136.000.000
d) 10.531.840
e) 105.318.400


15) (FUVEST) O preço de uma certa mercadoria sofre anualmente um acréscimo de 100% . Supondo que o preço atual seja R$ 100,00 , daqui a 3 anos o preço será.

a) R$ 300,00
b) R$ 400,00
c) R$ 600,00
d) R$ 800,00 (X)
e) R$ 1000,00


16) (FGV) Se uma mercadoria sofre dois descontos sucessivos de 15% e depois um acréscimo de 8% , seu preço final , em relação ao preço inicial:

a) aumentou de 22%
b) decresceu de 21,97% (X)
c) aumentou de 21,97%
d) decresceu de 23%
e) decresceu de 24%


17) (FGV) Uma fábrica de sapatos produz certo tipo de sapatos por R$ 18,00 o par , vendendo por R$ 25,00 o par . Com este preço , tem havido uma demanda de 2000 pares mensais . O fabricante pensa em elevar o preço em R$ 2,10. Com isto as vendas sofrerão uma queda de 200 pares . Com esse aumento no preço de venda seu lucro mensal:

a) cairá em 10%
b) aumentará em 20%
c) aumentará em 17% (X)
d) cairá em 20%
e) cairá em 17%


18) (FGV) Se João emagrecesse 10 kg , ele passaria a ter 75% do seu peso atual . Então , seu peso atual é:

a) inferior a 30 kg
b) 75 kg
c) 50 kg
d) superior a 75 kg
e) 40 kg (X)


19) (FGV) Um indivíduo ao engordar passou a ter 38% a mais em seu peso . Se tivesse engordado de tal maneira a aumentar seu peso em apenas 15%, estaria pesando 18,4 kg a menos . Qual era seu peso original ?

a) 50 kg
b) 60 kg
c) 70 kg
d) 80 kg (X)
e) 40 kg


20) (FGV) Num colégio com 1000 alunos , 65% dos quais são do sexo masculino , todos os estudantes foram convidados a opinar sobre o novo plano econômico do governo . Apurados os resultados , verificou-se que 40% dos homens e 50% das mulheres manifestaram-se favoravelmente ao plano . A porcentagem de estudantes favoráveis ao plano vale:

a) 43,5% (X)
b) 45%
c) 90%
d) 17,5%
e) 26%


21) (PUC) Em uma certa comunidade existem 200.000 professores de 1º e 2º graus que trabalham na rede oficial do Estado, 25.000 professores de 1º e 2º graus que trabalham na rede particular de ensino e 12.000 professores de 3º grau . Se 2,5% dos professores da rede oficial trabalham na rede particular , se 0,25% dos professores da rede oficial trabalham no 3º grau , e se 2% dos professores da rede particular trabalham no 3º grau , quantos professores possui essa comunidade , se apenas 200 professores trabalham , simultaneamente , na rede pública , particular , e no 3º grau ?

a) 213200
b) 231200 (X)
c) 212300
d) 223100
e) 231000


22) (ESPM) O salário médio de uma indústria de 354 funcionários é de R$ 3.300,00 . Se a indústria der um aumento de 20% para cada funcionário que possui , qual será o novo salário médio ?



a) R$ 3.690,00
b) R$ 369,00
c) R$ 396,00
d) R$ 3.960,00 (X)
e) n.d.a


23) (OSEC) Em apenas 6 meses o preço de um litro de gasolina teve 320% de aumento. Como esse preço era inicialmente de R$ 0,25 , ele passou a ser:

a) R$ 0,80
b) R$ 1,05 (X)c) R$ 1,50
d) R$ 2,80
e) R$ 2,85


24) (FUVEST) Um recipiente contém uma mistura de leite natural e de leite de soja num total de 200 litros , dos quais 25% são de leite natural . Qual é a quantidade de leite de soja que deve ser acrescentada à essa mistura para que ela venha a conter 20% de leite natural ?

a) 40
b) 43
c) 48
d) 50 (X)
e) 60


25) (FGV) Duas irmãs , Ana e Lúcia , têm uma conta de poupança conjunta . Do total do saldo , Ana tem 70% e Lúcia 30% . Tendo recebido um dinheiro extra , o pai das meninas resolveu fazer um depósito exatamente igual ao saldo na caderneta . Por uma questão de justiça , no entanto , ele disse às meninas que o depósito deveria ser dividido igualmente entre as duas . Nessas condições , a participação de Ana no novo saldo:

a) diminui para 60% (X)
b) diminuiu para 65%
c) permaneceu em 70%
d) aumentou para 80%
e) é impossível de ser calculada se não conhecermos o valor


26) (ESPM) O preço do papel sulfite , em relação ao primeiro semestre de 1989 , teve um aumento de 40% em agosto e um outro de 32% em setembro . No mês de novembro , teve um desconto de 25% . Qual seria o aumento do papel se ele fosse único?

a) 37%
b) 38,6% (X)
c) 36,8%
d) 35,4%
e) 34,5%


27) Um automóvel com velocidade de 80 km/h demora 3h para percorrer uma certa distância.Quanto o tempo demorará para percorrer a mesma distância um outro auto cuja velocidade é de 120 km/h?

a) 2 horas (X)
b) 3 horas
c) 4 horas
d) 5 horas
e) 6 horas


28) Uma roda de 30 dentes engrena com outra de 25 dentes. Quantas voltas dará esta última quando a primeira der 175 voltas.

a) 10 voltas
b) 110 voltas
c) 210 voltas (X)
d) 310 voltas
e) 410 voltas


29) Para forrar as paredes de uma sala são necessárias 20 peças de papel com 80 cm de largura cada. Quantas peças seriam necessárias se as peças tivessem 1m de largura?

a) 15 peças
b) 16 peças (X)
c) 17 peças
d) 18 peças
e) 19 peças