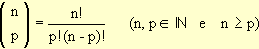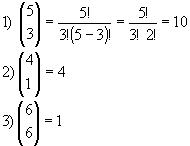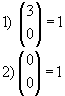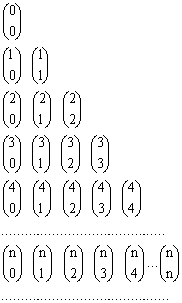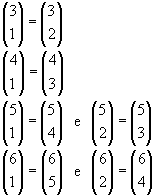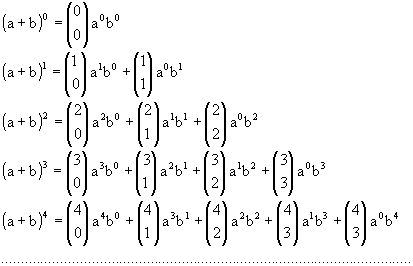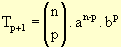Simples
Não ocorre a repetição de qualquer elemento em cada grupo de p elementos.
Fórmula: As(m,p) = m!/(m-p)!
Cálculo para o exemplo: As(4,2) = 4!/2!=24/2=12
Exemplo: Seja Z={A,B,C,D}, m=4 e p=2. Os arranjos simples desses 4 elementos tomados 2 a 2 são 12 grupos que não podem ter a repetição de qualquer elemento mas que podem aparecer na ordem trocada. Todos os agrupamentos estão no conjunto:
As={AB,AC,AD,BA,BC,BD,CA,CB,CD,DA,DB,DC}
Com repetição
Todos os elementos podem aparecer repetidos em cada grupo de p elementos.
Fórmula: Ar(m,p) = mp
Cálculo para o exemplo: Ar(4,2) = 42=16
Exemplo: Seja C={A,B,C,D}, m=4 e p=2. Os arranjos com repetição desses 4 elementos tomados 2 a 2 são 16 grupos que onde aparecem elementos repetidos em cada grupo. Todos os agrupamentos estão no conjunto:
Ar={AA,AB,AC,AD,BA,BB,BC,BD,CA,CB,CC,CD,DA,DB,DC,DD}
Condicional
Todos os elementos aparecem em cada grupo de p elementos, mas existe uma condição que deve ser satisfeita acerca de alguns elementos.
Fórmula: N=A(m1,p1).A(m-m1,p-p1)
Cálculo para o exemplo: N=A(3,2).A(7-3,4-2)=A(3,2).A(4,2)=6×12=72
Exemplo: Quantos arranjos com 4 elementos do conjunto {A,B,C,D,E,F,G}, começam com duas letras escolhidas no subconjunto {A,B,C}?
Aqui temos um total de m=7 letras, a taxa é p=4, o subconjunto escolhido tem m1=3 elementos e a taxa que este subconjunto será formado é p1=2. Com as letras A,B e C, tomadas 2 a 2, temos 6 grupos que estão no conjunto:
PABC = {AB,BA,AC,CA,BC,CB}
Com as letras D,E,F e G tomadas 2 a 2, temos 12 grupos que estão no conjunto:
PDEFG = {DE,DF,DG,ED,EF,EG,FD,FE,FG,GD,GE,GF}
Usando a regra do produto, teremos 72 possibilidades obtidas pela junção de um elemento do conjunto PABC com um elemento do conjunto PDEFG. Um típico arranjo para esta situação é CAFG.
---------------------------------------------------------
Permutações
Quando formamos agrupamentos com m elementos, de forma que os m elementos sejam distintos entre sí pela ordem. As permutações podem ser simples, com repetição ou circulares.
Simples
São agrupamentos com todos os m elementos distintos.
Fórmula: Ps(m) = m!
Cálculo para o exemplo: Ps(3) = 3!=6
Exemplo: Seja C={A,B,C} e m=3. As permutações simples desses 3 elementos são 6 agrupamentos que não podem ter a repetição de qualquer elemento em cada grupo mas podem aparecer na ordem trocada. Todos os agrupamentos estão no conjunto:
Ps={ABC,ACB,BAC,BCA,CAB,CBA}
Com repetição
Dentre os m elementos do conjunto C={x1,x2,x3,...,xn}, faremos a suposição que existem m1 iguais a x1, m2 iguais a x2, m3 iguais a x3, ... , mn iguais a xn, de modo que m1+m2+m3+...+mn=m.
Fórmula: Se m=m1+m2+m3+...+mn, então
Pr(m)=C(m,m1).C(m-m1,m2). C(m-m1-m2,m3) ... C(mn,mn)
Anagrama: Um anagrama é uma (outra) palavra construída com as mesmas letras da palavra original trocadas de posição.
Cálculo para o exemplo: m1=4, m2=2, m3=1, m4=1 e m=6, logo: Pr(6)=C(6,4).C(6-4,2).C(6-4-1,1)=C(6,4).C(2,2).C(1,1)=15
Exemplo: Quantos anagramas podemos formar com as 6 letras da palavra ARARAT. A letra A ocorre 3 vezes, a letra R ocorre 2 vezes e a letra T ocorre 1 vez. As permutações com repetição desses 3 elementos do conjunto C={A,R,T} em agrupamentos de 6 elementos são 15 grupos que contêm a repetição de todos os elementos de C aparecendo também na ordem trocada. Todos os agrupamentos estão no conjunto:
Pr={AAARRT,AAATRR,AAARTR,AARRTA,AARTTA,
AATRRA,AARRTA,ARAART,ARARAT,ARARTA,
ARAATR,ARAART,ARAATR,ATAARA,ATARAR}
Circulares
Ocorre quando obtemos grupos com m elementos distintos formando uma circunferência de círculo.
Fórmula: Pc(m) = (m-1)!
Cálculo para o exemplo: P(4)=3!=6
Exemplo: Seja um conjunto com 4 pessoas K={A,B,C,D}. De quantos modos distintos estas pessoas poderão sentar-se junto a uma mesa circular (pode ser retangular) para realizar o jantar sem que haja repetição das posições?
Se considerássemos todas as permutações simples possíveis com estas 4 pessoas, teriamos 24 grupos, apresentados no conjunto:
Pc={ABCD,ABDC,ACBD,ACDB,ADBC,ADCB,BACD,BADC,
BCAD,BCDA,BDAC,BDCA,CABD,CADB,CBAD,CBDA,
CDAB,CDBA, DABC,DACB,DBAC,DBCA,DCAB,DCBA}
Acontece que junto a uma mesa "circular" temos que:
ABCD=BCDA=CDAB=DABC
ABDC=BDCA=DCAB=CABD
ACBD=CBDA=BDAC=DACB
ACDB=CDBA=DBAC=BACD
ADBC=DBCA=BCAD=CADB
ADCB=DCBA=CBAD=BADC
o que significa existem somente 6 grupos distintos, dados por:
Pc={ABCD,ABDC,ACBD,ACDB,ADBC,ADCB}
Extraido do colaweb
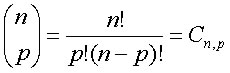. O número n é o numerador e o p, o denominador.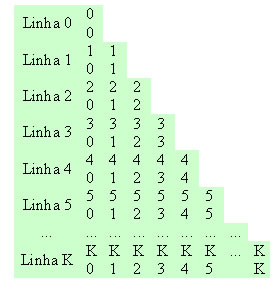
www.mundoeducacao.com.br
, podemos adotar o mesmo procedimento:
a partir da anterior, ou seja, de 
.
, chamamos de coeficiente binomial de classe p, do número n, o número 
, que indicamos por 
(lê-se: n sobre p). Podemos escrever:
e p + k = n então 
p-1 
, 
, 
e 
estão na linha 3 e os números binomiais 
, 
, 
, 
, ..., 
, ... estão na coluna 1.
= 1, todos os elementos da coluna 0 são iguais a 1.
= 1, o último elemento de cada linha é igual a 1.
.
, em que a, 
, é chamada binômio de Newton. Além disso:
.
