O triângulo de Pascal tem o objetivo de dispor os coeficientes binomiais, de modo que os coeficientes de mesmo numerador agrupem-se em uma mesma linha, e coeficientes de mesmo denominador agrupem-se na mesma coluna. O coeficiente binomial de dois números naturais é expresso por: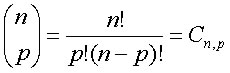 
. O número n é o numerador e o p, o denominador.
Observe a distribuição no triângulo:
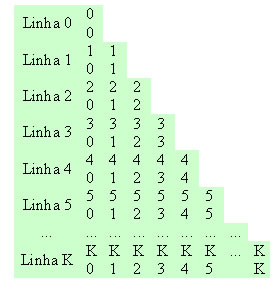
Calculando os valores dos coeficientes, obtemos outra forma de expressar o triângulo de Pascal ou Tartaglia:
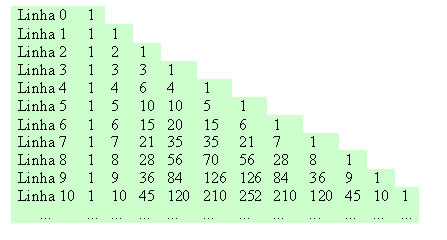
O triângulo apresenta algumas propriedades fundamentais. Veja:
Cada linha inicia e termina com o número 1.
Em cada linha, os termos equidistantes dos extremos possuem valor igual.
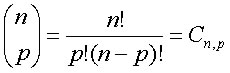. O número n é o numerador e o p, o denominador.Observe a distribuição no triângulo:
Calculando os valores dos coeficientes, obtemos outra forma de expressar o triângulo de Pascal ou Tartaglia:
O triângulo apresenta algumas propriedades fundamentais. Veja:
Cada linha inicia e termina com o número 1.
Em cada linha, os termos equidistantes dos extremos possuem valor igual.
Linha 8
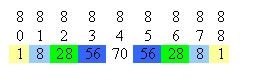
Linha 9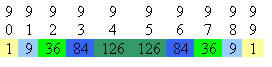
A partir da 2º linha, podemos perceber que cada elemento, com exceção do primeiro e do último, é igual à soma de dois elementos da linha anterior, a saber: o elemento imediatamente acima e o anterior. Observe:
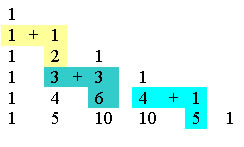
A soma dos elementos de cada linha do triângulo é a potência de base 2 elevado ao expoente referente à linha. Observe:
www.mundoeducacao.com.br
Linha 9
A partir da 2º linha, podemos perceber que cada elemento, com exceção do primeiro e do último, é igual à soma de dois elementos da linha anterior, a saber: o elemento imediatamente acima e o anterior. Observe:
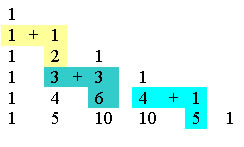
A soma dos elementos de cada linha do triângulo é a potência de base 2 elevado ao expoente referente à linha. Observe:
www.mundoeducacao.com.br
Nenhum comentário:
Postar um comentário