Curiosidade de Matemática

O Problema das Oito Caixas - Malba Tahan

O Problema das Oito Caixas e uma P.G. -Tudo a Ver!

Esse texto foi retirado da obra de Malba Tahan e chama-se "O Problema das Oito Caixas" que é um dos contos do matemático e escritor  Ali Iezid Izz-Edim Ibn Salim Hank Malba Tahan ou simplesmente "Malba Tahan" que é o pseudônimo do professor de Matemática Júlio César de Mello e Souza, nascido no Rio de Janeiro, em 1895, e falecido no ano de 1974, no Recife, aos 79 anos. Malba Tahan escreveu mais de uma centena de livros sobre Matemática Recreativa, Didática da Matemática, História da Matemática e Literatura Infanto-juvenil.   O texto é recomendado por muitos especialistas em educação para fazer parte dos conteúdos envolvendo a interdisciplinaridade e sobretudo para assessoramento no tópico  de progressão geométrica do ensino de matemática em nível médio. 

O PROBLEMA DAS OITO CAIXAS  

(conto do matemático: Malba Tahan)

Segundo uma lenda muito antiga, o célebre Califa Al Motacém Billah, rei dos árabes, chamou certa manhã o astucioso Sabag, seu vizir-tesoureiro, e disse-lhe em tom grave, como se ditasse uma sentença irrevogável:

— Dentro de poucas horas, meu caro vizir, receberei a visita do jovem Beremiz Samir, apelidado “o homem que calculava”. Não ignoras, certamente, que o talentoso Beremiz tem deslumbrado esta nossa gloriosa Bagdá com inequívocas demonstrações de seu incomparável engenho e de sua agudíssima inteligência. Os enigmas mais intrincados, os cálculos mais difíceis são, pelo exímio matemático, explicados e resolvidos em rápidos momentos.

É meu desejo presentear o ilustre Beremiz com avultada quantia. Gostaria, entretanto, de experimentar também a tão elogiada argúcia do calculista, propondo-lhe durante a nossa entrevista um problema que seja relacionado, de certo modo, com o prêmio que lhe darei em moedas de ouro. Um problema que deixasse o nosso visitante encantado, é verdade, mas também perplexo e confuso.

O vizir Sabag não era homem que se deixasse entibiar diante dos caprichos e fantasias do poderoso emir. Depois de ouvir, cabisbaixo e pensativo, as palavras do rei, ergueu o rosto bronzeado, fitou serenamente o glorioso califa, e assim falou:

— Escuto e obedeço, ó Príncipe dos Crentes! Pelo tom de vossas palavras, adivinho perfeitamente o rumo seguido pela caravana de vossas intenções. É vosso desejo premiar um sábio geômetra com valiosa quantia. Ressalta, dessa intenção, a generosidade sem par de vosso coração.  Quereis, entretanto, que este prêmio seja exorado com um problema original e inédito, capaz de surpreender o mais engenhoso dos matemáticos e de encantar o mais delicado dos filósofos. Essa lembrança põe em relevo a elegância de vossas atitudes, pois o visitante, ao ser arguido diante da corte, poderá mais uma vez demonstrar a pujança de seu engenho e o poderio de sua cultura.

Proferidas tais palavras, retirou-se o vizir para a sua sala de trabalho. Decorrido algum tempo, voltou à presença do rei, precedido de dois escravos núbios que conduziam pesada bandeja de prata. Repousavam sobre a bandeja oito caixas de madeira, todas do mesmo tamanho, numeradas de um até oito.

Não pequeno foi o espanto do califa de Bagdá ao ver aquele singular aparato. Qual seria a razão de ser daquelas caixas numeradas de um até oito? Que mistério, no domínio das contas e dos cálculos, poderiam elas envolver? Xeiques e nobres, que se achavam ao lado do rei, entreolhavam-se espantados.

Cabia ao honrado Sabag, ministro da corte, explicar o porquê daquela estranha preparação. Ouçamos, pois, o relato feito pelo digno vizir:

— Cada uma dessas caixas contém certo número de moedas. O total contido nas caixas é o prêmio que será oferecido ao calculista. As caixas, como podeis observar, estão numeradas de um até oito, e dispostas segundo o número de moedas que cada uma contém. Para esse arranjo das caixas, adotei a ordem crescente. Assim, a caixa designada pelo número 1 encerra o menor número de moedas; vem depois a que é indicada pelo número 2; a seguir aparece a de número 3, e assim por diante até a última, que encerra o maior número de moedas. Para evitar qualquer dúvida, direi desde logo que não é possível encontrar duas caixas com o mesmo número de moedas.

O califa, seriamente intrigado, interpelou o vizir:

— Não percebo, ó eloquente Sabag, que problema seria possível formular com esses dinares distribuídos por oito caixinhas. Por Allah! Não percebo!

O vizir Sabag, quando moço, fora professor primário e havia aprendido, diante das classes, a ensinar os iletrados, a esclarecer as dúvidas dos menos atilados e dirimir as questões sugeridas pelos mais espertos.

Firmemente resolvido a elucidar o glorioso soberano, o velho mestre-escola assim falou:

— Cumpre-me dizer, ó Rei do Tempo, que os dinares não foram distribuídos ao acaso pelas oito caixas. Cada caixa encerra certo número de moedas. São ao todo, portanto, oito quantias em dinares. Com as quantias distribuídas pelas oito caixas, podemos fazer qualquer pagamento, desde um dinar até o número total contido nas oito caixas, sem precisar abrir nenhuma caixa ou tocar em moeda alguma. Basta separar, da coleção que se acha sobre a bandeja, uma, duas, três, quatro ou mais caixas, e será obtido o total desejado.

— Iallah! É curioso! — comentou maravilhado o emir. — Segundo posso inferir de tua explicação, o arranjo dos dinares, distribuídos pelas oito caixas, permite que se possa retirar do total a quantia que se quiser, sem violar nenhuma das caixas, sem remover moeda alguma?

— Isso mesmo! — confirmou pressuroso o vizir. — Digamos que fosse vosso desejo retirar, por exemplo, do total a quantia de 212 dinares. Nada mais simples. No grupo das oito caixas há algumas cujas porções nelas contidas perfazem a soma de 212. Consistirá a dificuldade do problema, para cada caso, em determinar as caixas que devem ser separadas, a fim de que se obtenha uma determinada quantia, pois o que se fez para 212 poder-se-á fazer para 200, 49, 157, ou qualquer número inteiro até o total de moedas.

Feita breve pausa, a fim de permitir que o rei pudesse fixar ideias e refletir sobre o caso, o inteligente vizir rematou:

— Eis, ó Comendador dos Crentes, em resumo, o problema que poderia ser proposto, diante da corte, ao genial calculista: “Sabendo que estas caixas, numeradas de um até oito, contêm dinares em números que não se repetem; sabendo-se também que é possível efetuar qualquer pagamento até o número total de moedas, sem abrir nenhuma caixa, pergunta-se:

1º - Quantas moedas contém, respectivamente, cada uma das caixas?

2º - Como determinar, por meio do raciocínio, matematicamente certo, a quantia contida em cada uma?

3º - Qual o número total de moedas?

4º - Será possível resolver o mesmo problema distribuindo-se as moedas por um número menor de caixas?”

O divã do califado, isto é, o salão real das audiências, achava-se repleto de nobres e convidados quando, pelo soar surdo e solene do gongo, foi anunciada a visita de Beremiz Samir, “o homem que calculava”. No centro do suntuoso recinto, sobre luxuoso tapete, foi colocada a bandeja com as oito caixas que iriam servir de base para o problema.

Al-Motacém Billah, Príncipe dos Crentes, que se achava em seu trono de ouro e púrpura, rodeado de seus vizires e cádis, dirigiu ao matemático amistosa saudação:

— Sê bem-vindo, ó Beremiz! Sê bem-vindo sob a inspiração de Allah! Que a tua presença neste divã seja motivo de júbilo para todos os nossos amigos, e que de tuas palavras possamos colher as tâmaras deliciosas da sabedoria que eleva as almas e purifica os corações.

Decorreu um momento de impressionante silêncio. Competia ao visitante agradecer aquela honrosa saudação. Inclinando-se Beremiz diante do rei, assim falou:

— Allah badique, ia Sidi! — Deus vos conduza, ó Chefe! Admiro, estimo e exalto aqueles que governam com justiça, bondade e sabedoria. É esse o vosso caso, ó Emir dos Árabes, e todos os vossos súditos proclamam essa verdade. A vossa justiça assegura o poderio do Estado; a vossa bondade cria preciosas dedicações; e a vossa sabedoria fortalece e perpetua a confiança do povo. Ai daqueles cujos governantes são sábios, mas regem a vida pela injustiça das ações que praticam! Ai daqueles cujos chefes e dirigentes são justos, mas desconhecem a bondade! E Allah, o Clemente, se compadeça daqueles que se acham sob o jugo de homens ignorantes, pérfidos e iníquos.

— As tuas palavras, ó calculista — respondeu o rei mansamente — são para mim como brincos de ouro e rubis. Servem-me de estímulo e enchem-me de orgulho. Vou, mais uma vez, abusar de tua gentileza. Será um encanto, não só para mim, como para todos os nobres, vizires e xeiques que aqui se acham ouvir a tua palavra, a tua doutíssima opinião, sempre original e brilhante, sobre um problema aritmético que parece desafiar o engenho dos mais insignes matemáticos. Esse problema, formulado pelo vizir Sabag, poderia ser enunciado nos seguintes termos:

“Sobre aquela bandeja estão oito caixas. Cada caixa contém certo número de moedas, e não há duas caixas com o mesmo número de moedas. Afirma o vizir Sabag que a distribuição de moedas pelas oito caixas foi feita de modo a permitir que se possa do total, destacar qualquer quantia, desde um dinar, sem abrir nenhuma caixa, isto é, sem tocar nas moedas. Resta agora determinar quantas moedas contém cada caixa e qual o total de moedas. Para facilitar a exposição, as caixas estão numeradas de um até oito, segundo a ordem crescente das quantias que encerram”.

E o califa rematou, depois de breve pausa:

— Como orientarias, ó calculista, a solução desse engenhoso problema?

Beremiz Samir, “o homem que calculava”, como bom súdito, não se fez de rogado. Cruzou lentamente os braços, baixou o rosto e pôs-se a meditar. Depois de coordenar as ideias, iniciou a preleção sobre o caso, nos seguintes termos:

— Em nome de Allah, Clemente e Misericordioso! Esse problema é, realmente, um dos mais interessantes que tenho ouvido, e a sua solução, por ser simples e suave, põe em relevo a beleza e a simplicidade sem par da Matemática. Vejamos. A distribuição dos dinares pelas oito caixas foi feita de modo a permitir que separemos uma quantia qualquer, a partir de um dinar, destacando-se da coleção uma, duas, três ou mais caixas. Resta determinar o conteúdo de cada caixa. É evidente que a primeira caixa deve conter um dinar, pois do contrário não poderíamos destacar a unidade do total. Eis a conclusão algemada pela evidência: a caixa designada pelo número 1 contém um dinar.

A segunda caixa deverá conter, forçosamente, dois dinares, pois a quantia de um dinar não pode ser repetida, e se a segunda caixa tivesse três, quatro ou mais dinares não seria possível separar dois dinares do total. Conclusão: já conhecemos os conteúdos respectivos das duas primeiras caixas. Com auxílio dessas duas caixas podemos obter um, dois ou três dinares.

Passemos agora a terceira caixa. Quanto deveria conter? A resposta impõe-se imediatamente: quatro dinares. Com efeito, se a terceira caixa encerrasse mais de quatro dinares, não seria possível, conservando intactas as caixas, separar quatro dinares do total. Para as três primeiras, temos, portanto:

1ª caixa: 1 dinar;

2ª caixa: 2 dinares;

3ª caixa: 4 dinares.

Com auxílio dessas três caixas, podemos formar todas as quantias desde um até sete dinares. Sete representaria o total das três primeiras caixas, isto é, um mais dois mais quatro.

Repetindo o mesmo raciocínio, somos levados a afirmar que a caixa seguinte, isto é, a quarta, deverá conter oito dinares. A inclusão desta caixa com oito dinares permitirá separar do total todas as quantias desde um até quinze. O quinze é formado pelo conteúdo das quatro primeiras caixas.

E a quinta caixa? Não oferece o cálculo de seu conteúdo a menor dificuldade. Uma vez demonstrado que as quatro primeiras caixas totalizam quinze, é evidente que a quinta caixa deverá encerrar dezesseis dinares. A inclusão da quinta caixa ao grupo das quatro primeiras permite que formemos qualquer número desde um até trinta e um, inclusive. O total trinta e um é obtido pela soma das cinco primeiras.

Neste ponto fez o calculista uma pausa rapidíssima, e logo prosseguiu:

— Vejamos, pelo encadeamento natural de nosso raciocínio, se é possível descobrir uma lei, ou regra, que permita calcular os conteúdos respectivos das outras caixas restantes. Para isso convém recapitular:

1ª caixa: 1 moeda;

2ª caixa: 2 moedas;

3ª caixa: 4 moedas;

4ª caixa: 8 moedas;

5ª caixa: 16 moedas.

Observemos que cada caixa, a partir da segunda, contém sempre o dobro do número de moedas da caixa precedente. Dizem os matemáticos que os números 1, 2, 4, 8 e 16 formam uma progressão geométrica crescente, cuja razão é dois — um sistema binário, portanto. Dada à natureza do problema, é fácil provar que se mantém a mesma progressão fixando os conteúdos das quatro caixas seguintes. Temos então:

6ª caixa: 32 moedas;

7ª caixa: 64 moedas;

8ª caixa: 128 moedas;

E o total de moedas em todas as caixas, portanto, são 255.

— Uassalã!

  

Matéria Revisada, e Adaptado de Malba Tahan, O homem que calculava – Conquista, Rio, 1965.

O que essa famosa Progressão Geométrica tem a ver com os computadores? 

Tem tudo a ver, pois este é o sistema binário, que é a base de funcionamento dos computadores. Bit é a menor informação usada, correspondendo ao conteúdo de uma caixa, qualquer delas; byte é a informação (número) obtida com uma ou mais caixas escolhidas dentre essas oito. O sistema de oito bits (ou oito caixas, conforme a descrição) permite computar de 0 até 255. Os dez algarismos do sistema decimal ocupam apenas dez possibilidades, e as 245 restantes são usadas pelos analistas e programadores para corresponder a letras, sinais gráficos, comandos, etc. 

fonte:recordandomatematica.blogspot.com.br

Aula de Matematica

Aula Da 7ªA

View more presentations from Masclleide Paula.

Curiosidades da Matemática

Curiosidades

O epitáfio de Diofanto

Diofanto foi um matemático que viveu em Alexandria no século 3º. Foi o primeiro matemático grego a usar simbolismo algébrico e sua obra nos chegou através de fragmentos do seu livro "Aritmética". Em sua homenagem, chamamos de equações diofantinas as equações cujas soluções devem ser números inteiros.
Pouco sabemos sobre sua vida, mas existe uma charada que, dizem, teria sido gravada no seu túmulo: "Aqui jaz o matemático que passou um sexto da sua vida como menino. Um dozeavo da sua vida passou como rapaz. Depois viveu um sétimo da sua vida antes de se casar. Cinco anos após nasceu seu filho, com quem conviveu metade da sua vida. Depois da morte de seu filho, sofreu mais 4 anos antes de morrer." Quantos anos viveu Diofanto?

O último teorema de Fermat

Pierre de Fermat foi um grande matemático francês do século 17. Um dia, Fermat estava lendo um livro, "Aritmética" de Diofanto, onde o autor discutia as soluções inteiras para uma equação do tipo x² + y² = z². De acordo com o Teorema de Pitágoras, esses números constituem os lados de um triângulo retângulo. Existem infinitos números inteiros que satisfazem essa equação, como 3, 4 e 5 ou 5, 12 e 13.
Fermat começou a pensar se o mesmo seria verdadeiro para cubos ou biquadrados (quarta potência), isto é, se existiriam também soluções inteiras para equações do tipo x^3 + y^3 = z^3 ou, x^4 + y^4 = z^4 de modo geral, x^n + y^n = z^n. Ele escreveu na margem do seu livro: "É impossível separar um cubo em dois, ou um biquadrado em dois, ou, de um modo geral qualquer potência, exceto o quadrado, em duas potências com o mesmo expoente. Descobri uma demonstração demasiadamente maravilhosa, mas é demasiadamente comprida para caber nesta margem."Fermat morreu sem apresentar a demonstração Com isso, criou-se um problema que desafiaria os maiores matemáticos do mundo durante mais de três séculos e meio. Euler, o maior matemático do século 18, teve que reconhecer sua derrota. Recentemente, grandes matemáticos como Elkies e Faltings, quase o demonstraram. Muitos matematicos modernos começaram a duvidar que Fermat tivesse realmente demonstrado esse teorema. Até que, em 1995, um matemático americano, Andrew Wiles demonstrou definivamente o último teorema de Fermat, consagrando-se mundialmente.

Você é capaz de somar os algarismos de 1 a 100 em poucos minutos?

Carl Friedrich Gauss (1777-1855) aos 10 anos de idade respondeu rapidamente 5.050 ao seu professor surpreendendo-o pela sua grande habilidade na matemática. Em 1792, seu talento foi reconhecido pelo duque de Braunschweig, que lhe garantiu recursos para prosseguir o estudo de matemática. Gauss criou a geometria diferencial, e fez novas descobertas como a Lei da Reciprocidade Quadrática, que introduz o conceito de congruência e o Teorema Fundamental da Álgebra. Em 1801, publicou Disquisitiones Arithmeticae, seu tratado sobre a Teoria dos Números. No mesmo ano, calculou a órbita do asteróide Ceres. Com base em uma teoria que desenvolveu, previu corretamente onde e quando o Ceres deveria reaparecer. Morreu em 23 de fevereiro de 1855, sendo considerado o "Príncipe da Matemática".

Vejam abaixo a resolução proposta por Gauss
(isso aos 10 anos de idade):




Revolução Matemática - O cálculo diferencial e integral

O cálculo diferencial e integral, que Newton desenvolve ao mesmo tempo que o alemão Wilheim Leibniz (1646-1716), revoluciona a matemática. Para se saber a área de um círculo, utilizando a nova ferramenta, basta dividir esse círculo em quadrados iguais, bem pequenos. Em seguida, calcula-se a área de um quadrado e multiplica-se pelo número total de quadrados. Com isso, acha-se a área (ou o volume se for o caso, de qualquer figura). Os quadrados têm de ser infinitamente pequenos para encher toda a borda do círculo, e o número de quadrados precisa ser infinito. Portanto, a área total será uma soma de infinitos termos, tipo de soma que os gregos já sabiam fazer há mais de 2 mil anos.

Você sabia?
Que o maior número primo conhecido é , que tem 2.098.960 dígitos e foi descoberto em 01/06/1999 por Nayan Hafratwala, um participante do GIMPS, um projeto cooperativo para procurar primos de mersenne.

Que são conhecidos 51539600000 casas decimais de (Pi), calculadas por Y. Kamada e D. Takahashi, da Universidade de Tokio em 1997? E que em 21/08/1998 foi calculada pelo projeto Pihex a 5000000000000a. casa binária de (Pi).

Faça história na matemática!!!

Você poderia descobrir o mais desejado feito de toda a matemática: um novo número primo de Mersenne. A Electronic Frontier Foundation está oferecendo $100,000,00 para a primeira pessoa ou grupo que descobrir o décimo milionésimo dígito de um número primo! Você pode encontrar maiores informações em www.mersenne.org
http://ensinodematemtica.blogspot.com
Antonio Carlos Carneiro Barroso
Extraido do site www.exatas.mat.br

Mitose e meiose

Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso

Colégio Estadual Dinah Gonçalves

email accbarroso@hotmail.com

 www.ensinodematemtica.blogspot.com.br

www.accbarrosogestar.blogspot.com.br 

www.accbarrosogestar.wordpress.com        www.youtube.com/accbarroso1

     

Nosso organismo está sempre realizando divisões celulares. Há dois tipos de divisão celular, a mitose e a meiose, e nós realizamos tanto uma quanto outra, mas em situações diferentes. Para o estudante, é importante saber distinguir cada uma delas: mitose ou meiose?, eis a divisão, digo, a questão...Vamos ver quando e como realizamos cada uma delas.



Mitose
A mitose é um tipo de divisão celular que ocorre desde o surgimento da primeira célula do bebê (célula-ovo ou zigoto) até a nossa morte. Quando ainda estamos sendo gerados, no útero materno, é necessário que ocorra a duplicação das células a fim de formar o novo ser. A partir daí nunca mais paramos de realizar mitoses.

Esse processo é de suma importância para continuarmos a nos desenvolver, a crescer, a repor as células perdidas, como, por exemplo, ao sofrermos uma lesão na pele, ou perdermos células sanguíneas (hemácias) a cada 120 dias, etc.

A divisão da divisão
A mitose se inicia com uma célula diplóide (2n), ou seja, com o número total de cromossomos da espécie que no nosso caso são 46. Em seguida há um período denominado intérfase, em que ocorre a duplicação do material genético, para depois começar a divisão propriamente dita.

O processo de divisão é contínuo, mas para entendermos melhor a mitose, costumamos subdividi-la em fases, que são:

* prófase

* metáfase

* anáfase

* telófase



Na prófase, há uma certa "desorganização", pois a cromatina (material genético) inicia sua espiralização, transformando-se em cromossomos (contendo duas cromátides-irmãs). Há o desaparecimento do nucléolo, o rompimento da carioteca (membrana nuclear) e os centríolos migram para os pólos da célula.

Da metáfase à telófase
Na metáfase ocorre a espiralização máxima e os cromossomos encontram-se no centro da célula (plano equatorial), presos às fibras do fuso. Na anáfase, por sua vez, as cromátides-irmãs migram para os pólos opostos das células devido ao encurtamento das fibras do fuso.

Finalmente, na telófase ocorre a formação de duas células - filhas idênticas à célula-mãe (que originou todo o processo). Termina aí a cariocinese (divisão do núcleo) e inicia a citocinese (distribuição equivalente do citoplasma). Nesta etapa, reaparecem a carioteca, os nucléolos e os cromossomos voltam a desespiralizar-se.

Células sexuais
Já a meiose ocorre com a finalidade específica de produzirmos as células sexuais ou gametas (espermatozóide e óvulo). No homem, os espermatozóides se produzem à medida que são utilizados. Durante a ejaculação, eliminam-se em média 300 milhões de células.

Por sua vez, os óvulos já estão formados nos ovários da mulher desde o seu nascimento. São cerca de 400 mil, mas, normalmente, amadurece somente um a cada mês, após a puberdade.

Segunda divisão
A meiose também é dividida em etapas. Além disto, essa divisão é dupla. Na primeira divisão, ocorrem a prófase I, metáfase I, anáfase I e telófase I. Na segunda, a prófase II, metáfase II, anáfase II e telófase II.

A grosso modo, o que difere a meiose da mitose, além da formação de células com metade do número de cromossomos (n = 23), é que na prófase I acontecem subfases:

* leptóteno

* zigóteno

* paquíteno

* diplóteno

* diacinese



Elas são importantes, pois favorece o "crossing-over", ou seja, a mistura do material genético, com a quebra e troca de pontas entre os cromossomos. Mas, por que esse fato é importante? Para favorecer a variabilidade genética, o que garante a nossa diversidade.

É importante também que a meiose seja reducional, pois durante a fecundação (união do óvulo com o espermatozóide) forma-se um novo ser com 46 cromossomos, 23 vindos do pai e 23 da mãe. Desse modo, fica garantida a perpetuação da espécie.
* Cristina Faganelli Braun Seixas é bióloga e professora no Colégio Núcleo Educacional da Granja Viana.

Matemática para Cursos e Concursos

Nome: Matemática para Cursos e Concursos

Nome Original: Matemática para Cursos e Concursos

Autor: Desconhecido

Gênero: Cursos e Concursos

Ano de Lançamento:

Editora:

Sinopse: Aprenda definitivamente matemática - Conquiste sua vaga na Faculdade, passe em concursos - Exelente material de estudo!

{ 4Shared }

{ MegaUpload }

Curiosidade de Matemática

Curiosidades na Matemática

Aula de Matematica revisão para vestibular

Curiosidades sobre os números

Professor de Matemática no Colégio Estadual Dinah Gonçalves

E Biologia na rede privada de Salvador-Bahia

Professor Antonio Carlos carneiro Barroso

email accbarroso@hotmail.com

Blog HTTP://ensinodematemtica.blogspot.com e HTTP://accbarroso60.wordpress.com

http://accbarrosogestar.blogspot.com.br

Curiosidades sobre os números

Por Marcelo Rigonatto

Números e suas peculiaridades

A matemática é viva, intensa, impressionante e nos faz pensar, refletir e nos divertir. Conhecer a face divertida da matemática, com suas curiosidades e revelações, é fundamental para despertar o gosto por essa ciência fascinante que geralmente é vista com maus olhos. Vejamos algumas curiosidades que envolvem os números e quanta coisa interessante deixamos de aprender por achar que diversão e matemática não se misturam.

1. Raízes de números quadrados perfeitos.

Observe os seguintes pares de quadrados perfeitos:

144 e 441 (Note o que esses números apresentam em comum)

Extraindo a raiz quadrada de cada um deles, obtemos:

O que você consegue perceber?

Veja mais dois pares de quadrados perfeitos:

169 e 961

Extraindo as raízes de cada um, teremos:

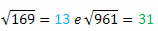
Conseguiu observar o que ocorre?

Veja que 144 e 441, 169 e 961 são pares de quadrados perfeitos compostos pelos mesmos algarismos só que escritos de trás para frente. O interessante é que suas respectivas raízes também apresentam essa característica.

Observe mais um exemplo:

Os pares de quadrados perfeitos 14884 e 48841 apresentam os mesmos algarismos só que escritos de trás para frente.

Calculando a raiz quadrada de cada um, temos:


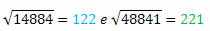
Suas raízes também apresentam os mesmos algarismos só que escritos em ordem inversa.

2. O número mágico 1089.

Vejamos o motivo de esse número ser chamado de número mágico.

Escreva um número de três algarismos distintos (diferentes).

598, por exemplo.

Escreva este número de trás para frente e subtraia o menor do maior.

895 – 598 = 297

Agora, inverta também esse resultado e efetue a adição.

792 + 297 = 1089

Independente do número escolhido, teremos sempre como resultado final o número 1089. Mas lembre-se, só vale para números de três algarismos distintos. Se utilizarmos, por exemplo, 555 ou 988 a propriedade não será válida.

3. A forma pitagórica de calcular potências.

Pitágoras foi um grande matemático que se dedicou ao estudo geométrico, trigonométrico e dos números. Dentre seus inúmeros estudos ele descobriu outra forma de se calcular potências com expoente 2. Depois de muito estudo e observação, notou que qualquer potência de números naturais do tipo n2 pode ser obtida somando os n primeiros números naturais ímpares. Veja como funciona:

a) 6² = 1 + 3 + 5 + 7 + 9 + 11 = 36
b) 7² = 1 + 3 + 5 + 7 + 9 + 11 + 13 = 49
c) 4² = 1 + 3 + 5 + 7 = 16
d) 5² = 1 + 3 + 5 + 7 + 9 = 25

Famoso Diálogo de Gandhi com Seu Professor Arrogante

Mahatma Gandhi

Diálogo de Gandhi com Seu Professor Arrogante

Através de muitas pesquisas na rede internet, soubemos que Mahatma Gandhi (1869-1948), nascido na Índia Britânica, quando estudava Direito numa instituição chamada: College London na cidade de Londres, Inglaterra, ele tinha um professor chamado: “Peters” que  julgava não gostar dele,  mas Gandhi nunca baixou a sua cabeça, e eram vários os seus contatos e reencontros, os quais muitas vezes eram tensos e até por vezes depressivos.

Um dia, o seu professor estava se alimentando no refeitório da universidade e casualmente Gandhi (aluno na época), sentou-se à mesma mesa com ele.  Então, o mestre como não teria ficado satisfeito com a coincidência do encontro e talvez querendo até menosprezá-lo, apresentou a seguinte indagação:

O professor disse-lhe em tom de deboche:

Senhor Gandhi, você não sabe que um porco e um pássaro nunca comem juntos?  - Ok. querido Professor,  já vou voando… - E, mudou-se de mesa no mesmo instante ....

O professor ficou aborrecido com o ocorrido, e resolveu vingar-se no exame seguinte, mas o aluno Gandhi respondeu brilhantemente a todas as perguntas formuladas, pois como sabemos, ele era um excelente estudante de direito. Então, o professor Peters resolveu fazer mais uma pergunta:  Senhor Gandhi, meu querido  e brilhante aluno, vou fazer-lhe outra pergunta: - Caso você estivesse transitando por uma rua e o senhor encontrasse  uma bolsa, e abrindo-a, encontrasse duas coisas: a sabedoria e muito dinheiro .... - Se pudesse escolher entre eles, com qual ficaria? 
- Claro que ficaria com o dinheiro! ... professor! ...
- Ah!... pois, eu no seu lugar ficaria com a sabedoria!…
- Tem razão professor, cada um fica com o que não tem!...

O professor furioso com tudo isso e disposto a se vingar, quando foi corrigir uma de suas avaliações de rotina, escreveu na sua prova “idiota” e entregou-a. - Gandhi  recebeu  a prova e sentou-se, e em alguns minutos depois,  foi ter com o professor e disse-lhe:
- Professor! ... O Senhor assinou a prova,  mas não pôs a nota…

Conclusão

Nesta história, vemos que a postura do grande líder e também grande pensador Mahatma Gandhi, embora na ocasião fosse um simples aluno, ele já tinha uma inteligência acima da média de seus pares e provavelmente também estaria a frente de seu professor.  Esse relato, no qual ele venceu com as suas atitudes o seu mestre, realmente aconteceu naquela escola da Inglaterra. O que fica aqui enfatizado nesse diálogo é que essa relação professor-aluno sempre foi e ainda continua sendo tensa para ambos os lados, tendo em vista que alguns professores ou mestres, se colocam como onipotentes, ou seja, aqueles que sabem tudo e que sempre tem razão em todos os sentidos, e muitas vezes acham que os seus alunos nunca sabem nada, mas isso, sabemos que muitas vezes não é verídico, como ocorreu no caso exposto.  Hoje, essa relação já vem sendo muito discutida e até retificada, e o bom professor, sempre aprende com os seus alunos.  Ele é sempre o mediador e o facilitador para o aprendizado de seus discentes. Criar um clima agradável, de respeito e cooperação entre todos deve ser o norteador de todo mestre que preza pelo ensino de qualidade, pois, acreditamos que isso facilitará muito o aprendizado de todos.  Acreditamos que o aluno Gandhi daquela conceituada escola, com toda a sua capacidade e inteligência, possa ter causado um desconforto para com seu professor, que sentiu-se inseguro com as suas atitudes, que de certo modo confrontaram como o modo de agir e pensar do seu mestre. Talvez nesse episódio, o professor pudesse estabelecer uma relação cordial e respeitosa com o seu aluno e provavelmente ele poderia até ajudá-lo no aprendizado e relacionamento com os demais alunos que frequentavam aquela famosa escola naquela ocasião.

fonte:recordandomatematica.blogspot.com.br