Média Aritmética - Exercícios resolvidos
01. Calcular a média aritmética entre os números 3, 4, 6, 9 e 13.
RESOLUÇÃO: A média aritmética é 7.
02. Calcular a média aritmética ponderada dos números 35, 20 e 10.
RESOLUÇÃO: A média aritmética ponderada é 18
03. a) Calcular a média aritmética Ma, a média geométrica Mg e a média harmônica Mh dos números 2 e 8.
b) Compare os três resultados
RESOLUÇÃO: a) Ma = 5; Mg = 4; Mh = 3,2
b) Ma > Mg > Mh
04. (ITA) Sabe-se que a média harmônica entre o raio e a altura de um cilindro de revolução vale 4. Quanto valerá a razão entre o volume e a área total do cilindro?
a) 1
b) 2
c) 2,5
d) 3
e) 3,5
RESPOSTA: A
05. Comprei 5 doces a R$ 1,80 cada um, 3 doces a R$ 1,50 e 2 doces a R$ 2,00 cada. O preço médio, por doce, foi de:
a) R$ 1,75
b) R$ 1,85
c) R$ 1,93
d) R$ 2,00
e) R$ 2,40
RESPOSTA: A
06. Uma empresa de embalagem mistura x kg de café tipo A, que custa 4 reais por quilograma, com y kg de café do tipo B, que custa 3,20 reais por quilograma. Calcular o custo de um quilograma dessa mistura quando:
a) x = y = 5
b) x = 6 e y = 4
c) x = 2 e y = 8
RESOLUÇÃO: a) R$ 3,60
b) R$ 3,68
c) R$ 3,36
07. (PUCCAMP - 98) Sabe-se que os números x e y fazem parte de um conjunto de 100 números, cuja média aritmética é 9,83. Retirando-se x e y desse conjunto, a média aritmética dos números restantes será 8,5. Se 3x - 2y = 125, então:
a) x = 75
b) y = 55
c) x = 85
d) y = 56
e) x = 95
RESPOSTA: C
08. (FUVEST) Sabe-se que a média aritmética de 5 números inteiros distintos, estritamente positivos, é 16. O maior valor que um desses inteiros pode assumir é:
a) 16
b) 20
c) 50
d) 70
e) 100
RESPOSTA: D
09. (VUNESP) Suponha que o país A receba de volta uma parte de seu território T, que por certo tempo esteve sob a administração do país B, devido a um tratado entre A e B. Estimemos a população de A, antes de receber T, em 1,2 bilhão de habitantes, e a de T em 6 milhões de habitantes. Se as médias de idade das populações A e T, antes de se reunirem, eram, respectivamente, 30 anos e 25 anos, mostre que a média de idade após a reunião é superior a 29,9 anos.
RESOLUÇÃO: Média final = 29,975 > 29,9
10. (FUVEST) Numa classe com vinte alunos, as notas do exame final podiam variar de 0 a 100 e a nota mínima para aprovação era 70. Realizado o exame, verificou-se que 8 alunos foram reprovados. A média aritmética das notas desses oito alunos foi 65, enquanto que a média dos aprovados foi 77. Após a divulgação dos resultados, o professor verificou que uma questão havia sido mal formulada e decidiu atribuir 5 pontos a mais para todos os alunos. Com essa decisão, a média dos aprovados passou a ser 80 e a dos reprovados 68,8.
a) Calcule a média aritmética das notas da classe toda antes da atribuição dos cinco pontos extras.
b) Com a atribuição dos cinco pontos extras, quantos alunos, inicialmente reprovados, atingiram nota para a aprovação?
RESOLUÇÃO: a) 72,2
b) 3
www.colaweb.com
Esse é o blog do Professor de Matemática Carlos Barroso. Trabalho no Colégio Estadual Dinah Gonçalves . Valéria-Salvador-Bahia .Inscreva-se Já no meu canal www.youtube.com/accbarroso1 e receba as videoaulas de Matemática.
Mostrando postagens com marcador Estatistica. Mostrar todas as postagens
Mostrando postagens com marcador Estatistica. Mostrar todas as postagens
sexta-feira, 3 de setembro de 2021
quarta-feira, 22 de julho de 2020
Freqüência Absoluta
Quando queremos levantar dados estatísticos devemos seguir os seguintes passos:
Escolher uma população estatística
• Classificar os dados escolhidos sobre uma população estatística.
• Escolher uma característica a ser observada na população. Essa característica é chamada de característica estatística.
• Elaborar uma tabela de dados com as características estatísticas.
Veja o exemplo:
Considere um grupo de 10 adolescentes de um colégio estadual. Iremos pesquisar dentre eles quantos lêem 2 livros por mês, quantos lêem 1 livro por mês e quantos não lêem. O quadro abaixo mostra essa pesquisa. Veja o resultado:
Dos 10 adolescentes que participaram da pesquisa:
5 lêem 2 livros por mês.
3 lêem 1 livro por mês.
2 não tem o hábito da leitura.
Veja o que podemos coletar dessa pesquisa:
População estatística: grupo dos 10 adolescentes.
Unidade estatística: cada adolescente que pertence ao grupo.
Variável estatística: quantidade de livros lidos por mês.
Quantidade de livros lidos (xi) Quantidade de adolescentes (Fi)
2 5
1 3
0 2
Total = 10
A primeira coluna contém os valores de xi que são as quantidades de livros lidos por mês e na segunda coluna contém os valores de Fi que é a quantidade de adolescentes que lêem livros durante o mês.
Os valores de Fi é a freqüência absoluta, ou seja, é o número de vezes que a variável estatística assume o valor Fi.
Observando os exemplos da tabela dizemos que:
A freqüência absoluta dos adolescentes que lêem 1 livro por mês é 3.
A freqüência absoluta dos adolescentes que lêem 0 livros por mês é 2.
Por Danielle de Miranda
Escolher uma população estatística
• Classificar os dados escolhidos sobre uma população estatística.
• Escolher uma característica a ser observada na população. Essa característica é chamada de característica estatística.
• Elaborar uma tabela de dados com as características estatísticas.
Veja o exemplo:
Considere um grupo de 10 adolescentes de um colégio estadual. Iremos pesquisar dentre eles quantos lêem 2 livros por mês, quantos lêem 1 livro por mês e quantos não lêem. O quadro abaixo mostra essa pesquisa. Veja o resultado:
Dos 10 adolescentes que participaram da pesquisa:
5 lêem 2 livros por mês.
3 lêem 1 livro por mês.
2 não tem o hábito da leitura.
Veja o que podemos coletar dessa pesquisa:
População estatística: grupo dos 10 adolescentes.
Unidade estatística: cada adolescente que pertence ao grupo.
Variável estatística: quantidade de livros lidos por mês.
Quantidade de livros lidos (xi) Quantidade de adolescentes (Fi)
2 5
1 3
0 2
Total = 10
A primeira coluna contém os valores de xi que são as quantidades de livros lidos por mês e na segunda coluna contém os valores de Fi que é a quantidade de adolescentes que lêem livros durante o mês.
Os valores de Fi é a freqüência absoluta, ou seja, é o número de vezes que a variável estatística assume o valor Fi.
Observando os exemplos da tabela dizemos que:
A freqüência absoluta dos adolescentes que lêem 1 livro por mês é 3.
A freqüência absoluta dos adolescentes que lêem 0 livros por mês é 2.
Por Danielle de Miranda
terça-feira, 21 de julho de 2020
Moda e Mediana
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
A Estatística está presente em diversas situações cotidianas e setores da sociedade, dessa forma, é conteúdo essencial em provas de concursos públicos. A moda e a mediana são elementos importantes na análise de dados pesquisacionais. Essas duas modalidades são utilizadas na determinação de medidas de tendência central.
A moda diz respeito ao valor que mais se repete na sequência dos dados e a mediana é caracterizada pela medida do termo central. Para que sejam determinados os valores da moda e da mediana, devemos organizar os dados em rol, isto é, organizá-los em sequências.
Moda
Exemplo 1
Em uma cidade, foram registradas as seguintes temperaturas médias no período da manhã durante 10 dias:
10 ºC, 13 ºC, 14 ºC, 15 ºC, 17 ºC, 17 ºC, 17 ºC, 18 ºC, 22 ºC, 23 ºC
Verifique que a temperatura de 17 ºC é a moda da sequência, pois é um valor com maior repetição.
Exemplo 2
Em uma sala do 7º ano, as notas dos alunos foram as seguintes: 5,5; 6,0; 4,0; 6,0; 8,0; 7,0; 5,8; 6,0; 6,1; 7,5; 6,0; 6,4; 7,2.
Organizando as notas em sequência crescente:
4,0 – 5,5 – 5,8 – 6,0 – 6,0 – 6,0 – 6,0 – 6,1 – 6,4 – 7,0 – 7,2 – 7,5 – 8,0 – 8,2
Na sequência de notas, temos que a de valor 6,0 obteve a maior frequência, resultando na moda dos valores.
Mediana
Na determinação da mediana temos a seguinte condição:
Se os n números da sequência forem ímpares, a mediana será o termo central.
Se os n números da sequência forem pares, a mediana será calculada através da média aritmética entre as duas notas centrais.
Exemplo 1
A altura de sete modelos foi registrada e anotada: 1,42 – 1,46 – 1,58 – 1,45 – 1,50 – 1,51 – 1,49.
Organizando as alturas em sequência crescente:
1,42 – 1,45 – 1,46 – 1,49 – 1,50 – 1,51 – 1,58
Como o número de alturas é ímpar, devemos localizar a medida da altura central. Portanto, a mediana das alturas é 1,49 metros.
Exemplo 2
Vamos considerar que o número de alturas colocadas em ordem, seja de seis modelos. Veja:
1,42 – 1,45 – 1,46 – 1,49 – 1,50 – 1,51 – 1,52 – 1,58
Nesse caso, onde o número seja par, devemos localizar as duas medidas centrais e calcular a média aritmética.
1,42 – 1,45 – 1,46 – 1,47 – 1,50 – 1,51 – 1,52 – 1,58
Me = (1,47 + 1,50) / 2
Me = 2,97 / 2
Me = 1,48
A mediana das alturas é igual a 1,48 metros.
www.bancodeconcursos.com
segunda-feira, 13 de julho de 2020
A mediana e a amplitude inter-quartis
Uma outra forma de sumarizar dados é em termos dos quantis ou
percentis. Essas medidas são particularmente úteis para
dados não simétricos.
A mediana (ou percentil 50) é definida como o valor que divide os dados ordenados ao meio, i.e. metade dos dados têm valores maiores do que a mediana, a outra metade tem valores menores do que a mediana.
Adicionalmente, os quartis inferior e superior, Q1 e Q3, são definidos como os valores abaixo dos quais estão um quarto e três quartos, respectivamente, dos dados.
Estes três valores são frequentemente usados para resumir os dados juntamente com o mínimo e o máximo.
Eles são obtidos ordenando os dados do menor para o maior, e então conta-se o número apropriado de observações: ou seja é ,
,
 e
e
 para o quartil inferior, mediana
e quartil superior, respectivamente.
para o quartil inferior, mediana
e quartil superior, respectivamente.
Para um número par de observações, a mediana é a média dos valores do meio (e analogamente para os quartis inferior e superior).
A medidade de dispersão é a amplitude inter-quartis, IQR Q3
Q3
 Q1, i.e. é a diferença entre o quartil superior e o inferior.
Q1, i.e. é a diferença entre o quartil superior e o inferior.
Exemplo. O número de crianças em 19 famílias foi
 valor, i.e. 3 crianças.
valor, i.e. 3 crianças.
O quartil inferior e superior são os valores e
e
 , i.e. 2 e 6 crianças,
portanto amplitude inter-quartil é de 4 crianças. Note que 50%
dos dados estão entre os quartis inferior e superior.
, i.e. 2 e 6 crianças,
portanto amplitude inter-quartil é de 4 crianças. Note que 50%
dos dados estão entre os quartis inferior e superior.
leg.ufpr.br
A mediana (ou percentil 50) é definida como o valor que divide os dados ordenados ao meio, i.e. metade dos dados têm valores maiores do que a mediana, a outra metade tem valores menores do que a mediana.
Adicionalmente, os quartis inferior e superior, Q1 e Q3, são definidos como os valores abaixo dos quais estão um quarto e três quartos, respectivamente, dos dados.
Estes três valores são frequentemente usados para resumir os dados juntamente com o mínimo e o máximo.
Eles são obtidos ordenando os dados do menor para o maior, e então conta-se o número apropriado de observações: ou seja é
Para um número par de observações, a mediana é a média dos valores do meio (e analogamente para os quartis inferior e superior).
A medidade de dispersão é a amplitude inter-quartis, IQR
Exemplo. O número de crianças em 19 famílias foi
0, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 4, 4, 5, 6, 6, 7, 8, 10
A mediana é o (19+1) / 2 = O quartil inferior e superior são os valores
leg.ufpr.br
domingo, 12 de julho de 2020
Variância e Desvio Padrão
A Variância e o Desvio Padrão são consideradas
medidas de dispersão e utilizadas nas situações em que grupos com médias
de valores iguais, possuem características diferentes. A Variância
estabelece os desvios em relação à média aritmética e o Desvio Padrão
analisa a regularidade dos valores. Vamos através de um exemplo prático,
demonstrar uma aplicação básica envolvendo as duas medidas.
Na preparação para os jogos Olímpicos de Atenas, três atletas do salto em altura ao realizarem um treinamento diário, consideraram seus quatro melhores saltos em centímetros. Veja:
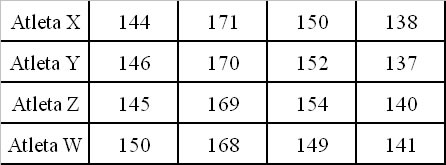
Dentre os atletas, a melhor média foi a do Atleta Z, veja:
Atleta X = (144 + 171 + 150 + 138) / 4 = 150,75
Atleta Y = (146 + 170 + 152 + 137) / 4 = 151,25
Atleta Z = (145 + 169 + 154 + 140) / 4 = 152
Atleta W = (150 + 167 + 149 + 141) / 4 = 151,75
Em situações que envolvam disputas olímpicas, o atleta com melhor média, às vezes não é considerado o mais indicado, pois verifica-se a questão da regularidade dos resultados obtidos. É referente a esses casos que aplicamos os cálculos ligados à Variância e ao Desvio Padrão.
Lembre-se de que o desvio padrão consiste na raiz quadrada da variância.
Cálculo da Variância e do Desvio Padrão
Na preparação para os jogos Olímpicos de Atenas, três atletas do salto em altura ao realizarem um treinamento diário, consideraram seus quatro melhores saltos em centímetros. Veja:

Dentre os atletas, a melhor média foi a do Atleta Z, veja:
Atleta X = (144 + 171 + 150 + 138) / 4 = 150,75
Atleta Y = (146 + 170 + 152 + 137) / 4 = 151,25
Atleta Z = (145 + 169 + 154 + 140) / 4 = 152
Atleta W = (150 + 167 + 149 + 141) / 4 = 151,75
Em situações que envolvam disputas olímpicas, o atleta com melhor média, às vezes não é considerado o mais indicado, pois verifica-se a questão da regularidade dos resultados obtidos. É referente a esses casos que aplicamos os cálculos ligados à Variância e ao Desvio Padrão.
Lembre-se de que o desvio padrão consiste na raiz quadrada da variância.
Cálculo da Variância e do Desvio Padrão
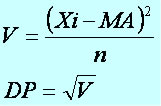
Atleta X

Atleta Y

Atleta Z
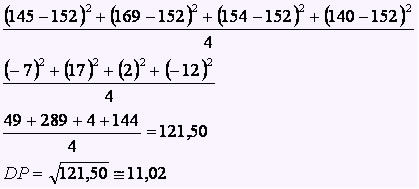
Atleta W

O atleta que obteve o menor Desvio Padrão deve ser considerado o de melhor regularidade em resultados. Dessa forma, temos que o atleta W se enquadra nessa condição de melhor regularidade.
quinta-feira, 2 de julho de 2020
Média Geométrica
Para calcularmos a média geométrica entre números
devemos realizar a multiplicação entre eles e, logo em seguida, extrair a
raiz com índice igual ao número de fatores utilizados na multiplicação.
Por exemplo, ao calcular a média geométrica dos números 2, 4 e 6,
efetuamos o seguinte cálculo:
A média geométrica é muito utilizada nas situações
envolvendo aumentos sucessivos. Por exemplo, vamos considerar um aumento
de salário sucessivo de 15% no primeiro mês, 12% no segundo mês e 21%
no terceiro mês.
Vamos determinar a média geométrica dos aumentos, mas para isso as taxas percentuais devem ser transformadas em taxa unitárias, observe:
15% = 1,15
12% = 1,12
21% = 1,21

O valor 1,1594 corresponde a taxa média de 15,94% de todos os aumentos sucessivos. Isso indica que se aplicarmos três vezes consecutivas a taxa de 15,94% corresponderá ao aumento sucessivo dos percentuais de 15%, 12% e 21%.
Suponhamos que o salário reajustado seja de R$ 600,00. Acompanhe os aumentos utilizando as duas opções de reajustes:
1ª opção
600,00 + 15% = 690,00
690,00 + 12% = 772,80
772,80 + 21% = 935,09
2ª opção
600,00 + 15,94% = 695,64
695,64 + 15,94% = 806,53
806,53 + 15,94% = 935,09
Vamos determinar a média geométrica dos aumentos, mas para isso as taxas percentuais devem ser transformadas em taxa unitárias, observe:
15% = 1,15
12% = 1,12
21% = 1,21

O valor 1,1594 corresponde a taxa média de 15,94% de todos os aumentos sucessivos. Isso indica que se aplicarmos três vezes consecutivas a taxa de 15,94% corresponderá ao aumento sucessivo dos percentuais de 15%, 12% e 21%.
Suponhamos que o salário reajustado seja de R$ 600,00. Acompanhe os aumentos utilizando as duas opções de reajustes:
1ª opção
600,00 + 15% = 690,00
690,00 + 12% = 772,80
772,80 + 21% = 935,09
2ª opção
600,00 + 15,94% = 695,64
695,64 + 15,94% = 806,53
806,53 + 15,94% = 935,09
Por Marcos Noé
Graduado em Matemática
Graduado em Matemática
quinta-feira, 4 de junho de 2020
Variáveis na Estatística
As variáveis nos estudos estatísticos são os valores que assumem
determinadas características dentro de uma pesquisa e podem ser
classificadas em qualitativas ou quantitativas.
As variáveis qualitativas não podem ser expressas numericamente, pois relacionam situações como a cor da pele, cor dos olhos, marca de refrigerante, marca de automóvel, preferência musical entre outras. Elas podem ser divididas em ordinais e nominais. As variáveis qualitativas ordinais, apesar de não serem numéricas, obedecem a uma relação de ordem, por exemplo: conceitos como ótimo, bom, regular e ruim, classe social, grau de instrução, etc. Já as variáveis qualitativas nominais não estão relacionadas à ordem, elas são identificadas apenas por nomes, por exemplo, as cores: vermelho, amarelo, preto, azul, rosa, verde, etc. Também como exemplo de nominais temos as marcas de carros, nome de bebidas, local de nascimento entre outros.
No caso das variáveis quantitativas usamos a representação numérica. Elas podem ser classificadas em discretas e contínuas. As variáveis quantitativas discretas acontecem relacionadas a situações limitadas, por exemplo: número de revistas vendidas, quantidade de consultas médicas, número de filhos de um casal. No caso das variáveis quantitativas contínuas, a abrangência pertence a um intervalo que se caracteriza por infinitos valores, como exemplo podemos citar: o peso de um produto, altura dos alunos de uma escola, velocidade de objetos, entre outras situações. Marcos Noé Pedro da Silva
As variáveis qualitativas não podem ser expressas numericamente, pois relacionam situações como a cor da pele, cor dos olhos, marca de refrigerante, marca de automóvel, preferência musical entre outras. Elas podem ser divididas em ordinais e nominais. As variáveis qualitativas ordinais, apesar de não serem numéricas, obedecem a uma relação de ordem, por exemplo: conceitos como ótimo, bom, regular e ruim, classe social, grau de instrução, etc. Já as variáveis qualitativas nominais não estão relacionadas à ordem, elas são identificadas apenas por nomes, por exemplo, as cores: vermelho, amarelo, preto, azul, rosa, verde, etc. Também como exemplo de nominais temos as marcas de carros, nome de bebidas, local de nascimento entre outros.
No caso das variáveis quantitativas usamos a representação numérica. Elas podem ser classificadas em discretas e contínuas. As variáveis quantitativas discretas acontecem relacionadas a situações limitadas, por exemplo: número de revistas vendidas, quantidade de consultas médicas, número de filhos de um casal. No caso das variáveis quantitativas contínuas, a abrangência pertence a um intervalo que se caracteriza por infinitos valores, como exemplo podemos citar: o peso de um produto, altura dos alunos de uma escola, velocidade de objetos, entre outras situações. Marcos Noé Pedro da Silva
sexta-feira, 22 de maio de 2020
Frequência Absoluta e Frequência Relativa
A Estatística é uma ferramenta matemática muito utilizada em vários setores da sociedade, organizando dados de pesquisas e apresentando informações claras e objetivas. Iremos através de um exemplo construir uma tabela de freqüência absoluta e freqüência relativa de uma variável.
Exemplo
Às pessoas presentes em um evento automobilístico foi feita a seguinte pergunta: Qual a sua marca de carro preferida?
Exemplo
Às pessoas presentes em um evento automobilístico foi feita a seguinte pergunta: Qual a sua marca de carro preferida?
| Pedro: Ford | Bruna: Peugeot | Anete: Ford | Paulo: Peugeot | Célio: Volks | Manoel: GM |
| Carlos: GM | Fred: Volks | Sérgio: Fiat | Gilson: GM | Rui: Fiat | Cláudia: Volks |
| Antônio : Fiat | Márcio: Volks | Marcelo: GM | Ana: Nissan | Geraldo: Volks | Rita: Ford |
| Pedro: Ford | Alicia: Renault | Meire: GM | Flávio: Peugeot | Lia: GM | Fabiano: Renault |
Construindo uma tabela para melhor dispor os dados:
Marcas
|
Frequência Absoluta (FA)
|
Frequência Relativa (FR)
|
Ford
|
4
|
16,7%
|
Fiat
|
3
|
12,5%
|
GM
|
6
|
25%
|
Nissan
|
1
|
4,2%
|
Peugeot
|
3
|
12,5%
|
Renault
|
2
|
8,3%
|
Volks
|
5
|
20,8%
|
Total
|
24
|
100%
|
Freqüência absoluta: quantas vezes cada marca de automóvel foi citada.
Freqüência relativa: é dada em porcentagem. A marca Ford tem freqüência relativa
4 em 24 ou 4/24 ou ~0,166 ou 16,66% ou 16,7%.
quarta-feira, 20 de maio de 2020
Moda e mediana
Ao realizar uma pesquisa é aconselhável realizar um estudo
estatístico dos dados apresentados. Através desse estudo podemos tirar
as conclusões necessárias sobre o universo pesquisado. A estatística
descritiva é a parte da estatística responsável por realizar essa
análise, apontando tendências de comportamento das variáveis, criando
gráficos e descrevendo as características dos conjuntos pesquisados.
Numa pesquisa, os dados tendem a se concentrar em torno dos valores centrais. Esses valores centrais são chamados de medidas de tendência central. São elas: Média, Moda e Mediana. Iremos abordar e conceituar Moda e Mediana.
Definição de Moda (Mo): é o valor que mais aparece num conjunto de dados.
Exemplo 1. Os dados abaixo se referem à idade de 20 alunos de uma turma de 6º ano.
Idade: {12, 11, 12, 13, 12, 11, 13, 12, 12, 11, 14, 13, 13, 12, 11, 12, 13, 14, 11, 14}
A moda desse conjunto de dados será a idade que mais aparece, ou seja:
Mo = 12 (pois é a idade que aparece mais vezes no conjunto)
Exemplo 2. A tabela abaixo apresenta as notas em matemática de uma turma de 30 alunos.
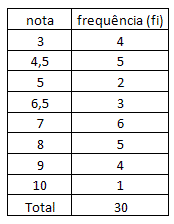
Na coluna da esquerda temos as notas na disciplina de matemática e na coluna da direita, quantos alunos obtiveram a respectiva nota. Dessa forma, podemos observar que a nota que mais aparece nesse conjunto de dados é 7. Portanto,
Mo = 7.
Exemplo 3. Os dados abaixo são referentes ao número dos calçados vendidos em uma loja num determinado dia.
{35, 33, 36, 35, 37, 36, 39, 40, 42, 43, 35, 36, 42}
Nesse caso, existem dois números de sapatos que aparecem mais vezes: 35 e 36. Logo, a moda pode ser:
Mo = 35 ou Mo = 36
Quando isso ocorre, dizemos que o conjunto de dados é bimodal.
Definição de Mediana (Md): é o valor (pertencente ou não ao conjunto de dados) que divide o conjunto de dados em dois subconjuntos de mesmo tamanho. De uma forma mais simples, é o valor que divide o conjunto de dados ao meio.
Para determinar a mediana de um conjunto de dados é necessário, primeiro, construir o rol. O rol é a ordenação do conjunto de dados em ordem crescente ou decrescente.
1. Mediana de um conjunto de dados com número de elementos ímpar.
Considere o conjunto de dados abaixo, referentes ao salário médio dos funcionários de uma empresa em reais.
Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980
Observe que nesse conjunto de dados temos 9 elementos, 9 salários. Primeiro devemos montar o rol:
Rol = {1100, 1200, 1210, 1250, 1300, 1450, 1500, 1600, 1980}
Quando o número de elementos do conjunto de dados for ímpar, a mediana é o valor que divide o conjunto ao meio, portanto Md = 1300. Observe que à esquerda e à direita de 1300 existem 4 elementos.
2. Mediana de um conjunto de dados com número de elementos ímpar.
Considere o conjunto de dados abaixo, referente ao salário médio dos funcionários de uma empresa.
Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980 1420
Rol = { 1100, 1200, 1210, 1250, 1300, 1420, 1450, 1500, 1600, 1980}
Nesse conjunto existem 10 elementos. Nesse caso a mediana será a média aritmética dos dois valores centrais. Note que tanto à direita como à esquerda dos dois valores centrais há 4 elementos. Assim,
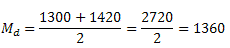
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Numa pesquisa, os dados tendem a se concentrar em torno dos valores centrais. Esses valores centrais são chamados de medidas de tendência central. São elas: Média, Moda e Mediana. Iremos abordar e conceituar Moda e Mediana.
Definição de Moda (Mo): é o valor que mais aparece num conjunto de dados.
Exemplo 1. Os dados abaixo se referem à idade de 20 alunos de uma turma de 6º ano.
Idade: {12, 11, 12, 13, 12, 11, 13, 12, 12, 11, 14, 13, 13, 12, 11, 12, 13, 14, 11, 14}
A moda desse conjunto de dados será a idade que mais aparece, ou seja:
Mo = 12 (pois é a idade que aparece mais vezes no conjunto)
Exemplo 2. A tabela abaixo apresenta as notas em matemática de uma turma de 30 alunos.

Na coluna da esquerda temos as notas na disciplina de matemática e na coluna da direita, quantos alunos obtiveram a respectiva nota. Dessa forma, podemos observar que a nota que mais aparece nesse conjunto de dados é 7. Portanto,
Mo = 7.
Exemplo 3. Os dados abaixo são referentes ao número dos calçados vendidos em uma loja num determinado dia.
{35, 33, 36, 35, 37, 36, 39, 40, 42, 43, 35, 36, 42}
Nesse caso, existem dois números de sapatos que aparecem mais vezes: 35 e 36. Logo, a moda pode ser:
Mo = 35 ou Mo = 36
Quando isso ocorre, dizemos que o conjunto de dados é bimodal.
Definição de Mediana (Md): é o valor (pertencente ou não ao conjunto de dados) que divide o conjunto de dados em dois subconjuntos de mesmo tamanho. De uma forma mais simples, é o valor que divide o conjunto de dados ao meio.
Para determinar a mediana de um conjunto de dados é necessário, primeiro, construir o rol. O rol é a ordenação do conjunto de dados em ordem crescente ou decrescente.
1. Mediana de um conjunto de dados com número de elementos ímpar.
Considere o conjunto de dados abaixo, referentes ao salário médio dos funcionários de uma empresa em reais.
Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980
Observe que nesse conjunto de dados temos 9 elementos, 9 salários. Primeiro devemos montar o rol:
Rol = {1100, 1200, 1210, 1250, 1300, 1450, 1500, 1600, 1980}
Quando o número de elementos do conjunto de dados for ímpar, a mediana é o valor que divide o conjunto ao meio, portanto Md = 1300. Observe que à esquerda e à direita de 1300 existem 4 elementos.
2. Mediana de um conjunto de dados com número de elementos ímpar.
Considere o conjunto de dados abaixo, referente ao salário médio dos funcionários de uma empresa.
Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980 1420
Rol = { 1100, 1200, 1210, 1250, 1300, 1420, 1450, 1500, 1600, 1980}
Nesse conjunto existem 10 elementos. Nesse caso a mediana será a média aritmética dos dois valores centrais. Note que tanto à direita como à esquerda dos dois valores centrais há 4 elementos. Assim,
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
terça-feira, 19 de maio de 2020
Média Aritmética de Intervalos
Em algumas situações estatísticas, os dados são
apresentados em intervalos agrupados. Dessa forma, o cálculo da média
aritmética é realizado de forma mais complexa. Nesse caso, temos que
determinar primeiramente a média de cada intervalo multiplicando o
resultado pela frequência absoluta do intervalo. O somatório desses
produtos deverá ser dividido pelo somatório da frequência absoluta,
constituindo a média dos valores agrupados em intervalos. Observe o
seguinte exemplo:
A tabela a seguir mostra a massa (em quilograma) de um grupo de pessoas. Os dados foram informados em intervalos. Veja:
A tabela a seguir mostra a massa (em quilograma) de um grupo de pessoas. Os dados foram informados em intervalos. Veja:

Determinando a média de cada intervalo:
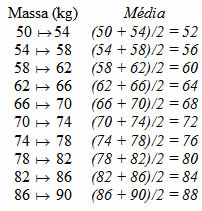
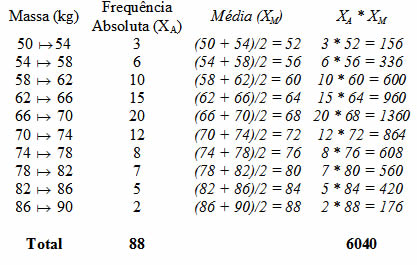
Média Aritmética = ∑(XA * XM) / ∑XA
Média Aritmética = 6040 / 88
Média Aritmética = 68,63 (aproximadamente)
A média aritmética envolvendo a massa (kg) das pessoas do grupo é de aproximadamente 68,63 kg.
Média Aritmética = 6040 / 88
Média Aritmética = 68,63 (aproximadamente)
A média aritmética envolvendo a massa (kg) das pessoas do grupo é de aproximadamente 68,63 kg.
Por Marcos Noé
Graduado em Matemático
Graduado em Matemático
Histograma
Na estatística, um histograma é uma representação gráfica da distribuição de frequências de uma massa de medições, normalmente um gráfico de barras verticais. É uma das Sete Ferramentas da Qualidade.
O histograma é um gráfico composto por retângulos justapostos em que a base de cada um deles corresponde ao intervalo de classe e a sua altura à respectiva freqüência. Quando o número de dados aumenta indefinidamente e o intervalo de classe tende a zero, a distribuição de freqüência passa para uma distribuição de densidade de probabilidades.
A construção de histogramas tem caráter preliminar em qualquer estudo e é um importante indicador da distribuição de dados. Podem indicar se uma distribuição aproxima-se de uma função normal, como pode indicar mistura de populações quando se apresentam bimodais.
Histograma:
Gráfico composto por duas linhas perpendiculares onde a altura representa o valor da grandeza, e as grandezas são colocadas na linha horizontal. Sobre cada uma levanta-se uma barra que termina na altura relativa ao valor de sua grandeza. Conhecido também como gráfico de barras.

Representação histográfica, constituída de uma série de retângulos justapostos que têm por base o intervalo de classe. A área de cada retângulo é proporcional à freqüência da classe correspondente e tem grande aceitação nos casos de distribuição contínua de freqüência.
O campo da computação, chamado, processamento de imagem, é um exemplo prático de como histogramas podem ser utilizados. Numa imagem a informação da quantidade de vezes que uma determinada cor se repete representa o histograma dessa imagem. Como as possibilidades de cores são altas, esse tipo de histograma é gerado com base numa foto preto e branco.Uma informação assim sobre a imagem é importante pois pode gerar parâmetros para a avaliação da qualidade da mesma, como nitidez, luminosidade e profundidade.
Etimologia
A etimologia da palavra histograma é incerta. Algumas vezes é dito que essa palavra deriva do termo grego histos "não erguido" (como os mastros do navio ou as barras verticais do histograma) egramma "desenhar, escrever, gravar". Também se fala que a palavra deriva de "historical diagram", Karl Pearson teria introduzido o termo em 1895.
Quartis
A mediana é o valor que divide a amostra em duas partes iguais, deixando exactamente 50% das observações de cada lado.
Também a poderíamos dividir em quatro partes iguais, cada uma contento 25% dos dados. Nesse caso cada uma das partes seria um quartil.

O primeiro quartil escreve-se abreviadamente Q1/4, correspondendo a 25% dos dados. O segundo quartil Q2/4, corresponde à mediana. O terceiro quartil Q3/4, corresponde a 75% das observações.
O seu cálculo é análogo ao da mediana. Começa-se por determinar a respectiva classe observando as frequências relativas acumuladas.

A amostra também pode ser divida em 10 partes de 10% cada, originando os decis ou em 100 partes de 1% obtendo-se os percentis.
1. Utilizando a Tabela 5, calcula:
- O primeiro quartil, Q1/4
- O segundo quartil, Q2/4
- O terceiro quartil, Q3/4
fonte:estatisticax.blogspot.com.br
Também a poderíamos dividir em quatro partes iguais, cada uma contento 25% dos dados. Nesse caso cada uma das partes seria um quartil.

O primeiro quartil escreve-se abreviadamente Q1/4, correspondendo a 25% dos dados. O segundo quartil Q2/4, corresponde à mediana. O terceiro quartil Q3/4, corresponde a 75% das observações.
O seu cálculo é análogo ao da mediana. Começa-se por determinar a respectiva classe observando as frequências relativas acumuladas.

A amostra também pode ser divida em 10 partes de 10% cada, originando os decis ou em 100 partes de 1% obtendo-se os percentis.
1. Utilizando a Tabela 5, calcula:
- O primeiro quartil, Q1/4
- O segundo quartil, Q2/4
- O terceiro quartil, Q3/4
fonte:estatisticax.blogspot.com.br
quarta-feira, 22 de abril de 2020
Diagramas de Venn na Estatística

John Venn (1834 - 1923)
O estudo e desenvolvimento da Estatística requerem um planejamento organizacional, em razão da importância significativa de uma pesquisa. O matemático inglês John Venn, criou um sistema de representação de diagramas no intuito de determinar uniões e intersecções, facilitando a organização e interpretação de dados pesquisados.
A representação através desses diagramas recebeu o nome de Diagramas de Venn em retribuição à sua grande contribuição para a matemática.
Utilizando o diagrama de Venn
Observe o exemplo:
Uma pesquisa sobre a preferência dos leitores de uma cidade em relação aos jornais A, B e C foi realizada. Foram entrevistados 360 leitores entre homens e mulheres maiores de 18 anos de idade. Os dados coletados na pesquisa foram os seguintes:
120 leem o jornal A.
170 leem o jornal B.
150 leem o jornal C.
40 leem o jornal A e B.
15 leem os jornais A e C.
30 leem os jornais B e C.
05 leem os jornais A, B e C.
Quantos leitores preferem ler somente o jornal A?
Resolução:
Vamos utilizar os diagramas de Venn para representar os dados da pesquisa.
A representação através desses diagramas recebeu o nome de Diagramas de Venn em retribuição à sua grande contribuição para a matemática.
Utilizando o diagrama de Venn
Observe o exemplo:
Uma pesquisa sobre a preferência dos leitores de uma cidade em relação aos jornais A, B e C foi realizada. Foram entrevistados 360 leitores entre homens e mulheres maiores de 18 anos de idade. Os dados coletados na pesquisa foram os seguintes:
120 leem o jornal A.
170 leem o jornal B.
150 leem o jornal C.
40 leem o jornal A e B.
15 leem os jornais A e C.
30 leem os jornais B e C.
05 leem os jornais A, B e C.
Quantos leitores preferem ler somente o jornal A?
Resolução:
Vamos utilizar os diagramas de Venn para representar os dados da pesquisa.

Exemplo 2
Podemos utilizar os diagramas de Venn para representar os conjuntos numéricos na Matemática.
N: conjunto dos números Naturais
Z: conjunto dos números Inteiros
Q: conjunto dos números Racionais
I: conjunto dos números Irracionais
R: conjunto dos números Reais
C: conjunto dos números Complexos

Por Marcos Noé
terça-feira, 21 de abril de 2020
Agrupamento de Dados em Intervalos
Os estudos estatísticos são responsáveis pela análise de informações através de tabelas informativas e representações gráficas, no intuito de fornecer clareza nos resultados obtidos. Os dados coletados são organizados em tabelas que detalham as frequências absoluta e relativa. Em algumas situações, a quantidade de informações diferenciadas torna inviável a construção de uma tabela com uma linha para cada representação de valor. Nesses casos optamos por agrupar os dados em intervalos de classes.
Para a melhor representação dessa situação iremos apresentar um grupo de pessoas, das quais suas alturas foram coletadas. Observe:
1. Amorim: 1,91
2. Antônio: 1,78
3. Bernardo: 1,69
4. Carlos: 1,82
5. Celso: 1,80
6. Danilo: 1,72
7. Douglas: 1,73
8. Daniel: 1,76
9. Everton: 1,77
10. Gabriel: 1,93
11. Gustavo: 1,84
12. Heitor: 1,87
13. Ítalo: 1,85
14. João Carlos: 1,89
15. João Vinicius: 1,70
16. Leonardo: 1,91
17. Lucas: 1,86
18. Marlon: 1,70
19. Orlando: 1,71
20. Pedro: 1,93
Para definirmos os intervalos, vamos realizar a subtração entre a maior e a menor altura: 1,94 – 1,69 = 0,25.
O número de intervalos deve ser sempre maior que quatro. No caso descrito, vamos estipular cinco intervalos de classe, dessa forma adicionamos 0,01 a 0,24 e dividimos por 5:
0,25 : 5 = 0,05. Veja os intervalos:
1,69  1,74 (1,69 + 0,05)
1,74 (1,69 + 0,05)
1,74 1,79 (1,74 + 0,05)
1,79 (1,74 + 0,05)
1,79 1,84 (1,79 + 0,05)
1,84 (1,79 + 0,05)
1,84 1,89 (1,84 + 0,05)
1,89 (1,84 + 0,05)
1,89 1,94 (1,89 + 1,94)
1,94 (1,89 + 1,94)
1,74
1,79
1,84
1,89
Importante: no intervalo 1,69

A tabela informa as alturas de acordo com os intervalos, a frequência absoluta e a frequência relativa e percentual.
Por Marcos Noé
segunda-feira, 20 de abril de 2020
Boxplot
O boxplot (gráfico de caixa) é um gráfico utilizado para avaliar a distribuição empírica do dados. O boxplot é formado pelo primeiro e terceiro quartil e pela mediana. As hastes inferiores e superiores se estendem, respectivamente, do quartil inferior até o menor valor não inferior ao limite inferior e do quartil superior até o maior valor não superior ao limite superior. Os limites são calculados da forma abaixo
Limite inferior:  .
.
 .
.
Limite superior:  .
.
 .
.
Para este caso, os pontos fora destes limites são considerados valores discrepantes (outliers) e são denotados por asterisco (*). A Figura a seguir apresenta um exemplo do formato de um boxplot.
O boxplot pode ainda ser utilizado para uma comparação visual entre dois ou mais grupos. Por exemplo, duas ou mais caixas são colocadas lado a lado e se compara a variabilidade entre elas, a mediana e assim por diante. Outro ponto importante é a diferença entre os quartis  que é uma medida da variabilidade dos dados.
que é uma medida da variabilidade dos dados.
 que é uma medida da variabilidade dos dados.
que é uma medida da variabilidade dos dados.
Exemplo 3.1.1: Na Tabela a seguir temos as medidas da altura de 20 hastes. Faça o boxplot correspondente.
| Dados da usinagem | |||
| 903,88 | 1036,92 | 1098,04 | 1011,26 |
| 1020,70 | 915,38 | 1014,53 | 1097,79 |
| 934,52 | 1214,08 | 993,45 | 1120,19 |
| 860,41 | 1039,19 | 950,38 | 941,83 |
| 936,78 | 1086,98 | 1144,94 | 1066,12 |
O boxplot é dado por
| Para entender como executar essa função do Software Action, você pode consultar o manual do usuário. fonte:www.portalaction.com.br | |||
Coeficiente de variação
Como o desvio padrão é expresso na mesma unidade dos dados observados em estudo, comparar duas ou mais séries de valores que estão em unidades de medida diferentes torna-se impossível. Para sanar essas dificuldades, podemos analisar a dispersão em termos relativos a seu valor médio, utilizando o coeficiente de variação de Pearson.
O coeficiente de variação é dado pela fórmula:

Onde,O coeficiente de variação é dado pela fórmula:

Cv → é o coeficiente de variação
s → é o desvio padrão
X ̅ → é a média dos dados
O coeficiente de variação é dado em %, por isso a fórmula é multiplicada por 100.
Observações:
O coeficiente de variação fornece a variação dos dados obtidos em relação à média. Quanto menor for o seu valor, mais homogêneos serão os dados. O coeficiente de variação é considerado baixo (apontando um conjunto de dados bem homogêneos) quando for menor ou igual a 25%. O fato de o coeficiente de variação ser dado em valor relativo nos permite comparar séries de valores que apresentam unidades de medida distintas.
Exemplo. Compare a variabilidade relativa do tempo de reação de um analgésico A com a variabilidade do peso das pessoas que se submeteram à dosagem desse analgésico. As médias e os desvios padrão foram:
Analgésico A: X ̅=3 min e s = 0,71
Peso das pessoas: X ̅=58,25 kg e s = 5,17
Solução: Vamos calcular o coeficiente de variação para cada item observado.
Cálculo para o tempo de reação do analgésico:

Cálculo para o peso das pessoas:

Comparando o coeficiente de variação do tempo de reação do analgésico e o do peso das pessoas, podemos concluir que os dados referentes ao peso são mais consistentes que os dados referentes ao tempo de reação do analgésico, ou ainda, que os dados referentes ao peso são mais homogêneos que os do tempo de reação do analgésico.
Por Marcelo Rigonatto
s → é o desvio padrão
X ̅ → é a média dos dados
O coeficiente de variação é dado em %, por isso a fórmula é multiplicada por 100.
Observações:
O coeficiente de variação fornece a variação dos dados obtidos em relação à média. Quanto menor for o seu valor, mais homogêneos serão os dados. O coeficiente de variação é considerado baixo (apontando um conjunto de dados bem homogêneos) quando for menor ou igual a 25%. O fato de o coeficiente de variação ser dado em valor relativo nos permite comparar séries de valores que apresentam unidades de medida distintas.
Exemplo. Compare a variabilidade relativa do tempo de reação de um analgésico A com a variabilidade do peso das pessoas que se submeteram à dosagem desse analgésico. As médias e os desvios padrão foram:
Analgésico A: X ̅=3 min e s = 0,71
Peso das pessoas: X ̅=58,25 kg e s = 5,17
Solução: Vamos calcular o coeficiente de variação para cada item observado.
Cálculo para o tempo de reação do analgésico:

Cálculo para o peso das pessoas:

Comparando o coeficiente de variação do tempo de reação do analgésico e o do peso das pessoas, podemos concluir que os dados referentes ao peso são mais consistentes que os dados referentes ao tempo de reação do analgésico, ou ainda, que os dados referentes ao peso são mais homogêneos que os do tempo de reação do analgésico.
terça-feira, 7 de abril de 2020
Moda e mediana
Ao realizar uma pesquisa é aconselhável realizar um estudo estatístico dos dados apresentados. Através desse estudo podemos tirar as conclusões necessárias sobre o universo pesquisado. A estatística descritiva é a parte da estatística responsável por realizar essa análise, apontando tendências de comportamento das variáveis, criando gráficos e descrevendo as características dos conjuntos pesquisados.
Numa pesquisa, os dados tendem a se concentrar em torno dos valores centrais. Esses valores centrais são chamados de medidas de tendência central. São elas: Média, Moda e Mediana. Iremos abordar e conceituar Moda e Mediana.
Definição de Moda (Mo): é o valor que mais aparece num conjunto de dados.
Exemplo 1. Os dados abaixo se referem à idade de 20 alunos de uma turma de 6º ano.
Idade: {12, 11, 12, 13, 12, 11, 13, 12, 12, 11, 14, 13, 13, 12, 11, 12, 13, 14, 11, 14}
A moda desse conjunto de dados será a idade que mais aparece, ou seja:
Mo = 12 (pois é a idade que aparece mais vezes no conjunto)
Exemplo 2. A tabela abaixo apresenta as notas em matemática de uma turma de 30 alunos.

Numa pesquisa, os dados tendem a se concentrar em torno dos valores centrais. Esses valores centrais são chamados de medidas de tendência central. São elas: Média, Moda e Mediana. Iremos abordar e conceituar Moda e Mediana.
Definição de Moda (Mo): é o valor que mais aparece num conjunto de dados.
Exemplo 1. Os dados abaixo se referem à idade de 20 alunos de uma turma de 6º ano.
Idade: {12, 11, 12, 13, 12, 11, 13, 12, 12, 11, 14, 13, 13, 12, 11, 12, 13, 14, 11, 14}
A moda desse conjunto de dados será a idade que mais aparece, ou seja:
Mo = 12 (pois é a idade que aparece mais vezes no conjunto)
Exemplo 2. A tabela abaixo apresenta as notas em matemática de uma turma de 30 alunos.

Na coluna da esquerda temos as notas na disciplina de matemática e na coluna da direita, quantos alunos obtiveram a respectiva nota. Dessa forma, podemos observar que a nota que mais aparece nesse conjunto de dados é 7. Portanto,
Mo = 7.
Exemplo 3. Os dados abaixo são referentes ao número dos calçados vendidos em uma loja num determinado dia.
{35, 33, 36, 35, 37, 36, 39, 40, 42, 43, 35, 36, 42}
Nesse caso, existem dois números de sapatos que aparecem mais vezes: 35 e 36. Logo, a moda pode ser:
Mo = 35 ou Mo = 36
Quando isso ocorre, dizemos que o conjunto de dados é bimodal.
Definição de Mediana (Md): é o valor (pertencente ou não ao conjunto de dados) que divide o conjunto de dados em dois subconjuntos de mesmo tamanho. De uma forma mais simples, é o valor que divide o conjunto de dados ao meio.
Para determinar a mediana de um conjunto de dados é necessário, primeiro, construir o rol. O rol é a ordenação do conjunto de dados em ordem crescente ou decrescente.
1. Mediana de um conjunto de dados com número de elementos ímpar.
Considere o conjunto de dados abaixo, referentes ao salário médio dos funcionários de uma empresa em reais.
Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980
Observe que nesse conjunto de dados temos 9 elementos, 9 salários. Primeiro devemos montar o rol:
Rol = {1100, 1200, 1210, 1250, 1300, 1450, 1500, 1600, 1980}
Quando o número de elementos do conjunto de dados for ímpar, a mediana é o valor que divide o conjunto ao meio, portanto Md = 1300. Observe que à esquerda e à direita de 1300 existem 4 elementos.
2. Mediana de um conjunto de dados com número de elementos ímpar.
Considere o conjunto de dados abaixo, referente ao salário médio dos funcionários de uma empresa.
Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980 1420
Rol = { 1100, 1200, 1210, 1250, 1300, 1420, 1450, 1500, 1600, 1980}
Nesse conjunto existem 10 elementos. Nesse caso a mediana será a média aritmética dos dois valores centrais. Note que tanto à direita como à esquerda dos dois valores centrais há 4 elementos. Assim,
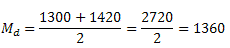
Mo = 7.
Exemplo 3. Os dados abaixo são referentes ao número dos calçados vendidos em uma loja num determinado dia.
{35, 33, 36, 35, 37, 36, 39, 40, 42, 43, 35, 36, 42}
Nesse caso, existem dois números de sapatos que aparecem mais vezes: 35 e 36. Logo, a moda pode ser:
Mo = 35 ou Mo = 36
Quando isso ocorre, dizemos que o conjunto de dados é bimodal.
Definição de Mediana (Md): é o valor (pertencente ou não ao conjunto de dados) que divide o conjunto de dados em dois subconjuntos de mesmo tamanho. De uma forma mais simples, é o valor que divide o conjunto de dados ao meio.
Para determinar a mediana de um conjunto de dados é necessário, primeiro, construir o rol. O rol é a ordenação do conjunto de dados em ordem crescente ou decrescente.
1. Mediana de um conjunto de dados com número de elementos ímpar.
Considere o conjunto de dados abaixo, referentes ao salário médio dos funcionários de uma empresa em reais.
Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980
Observe que nesse conjunto de dados temos 9 elementos, 9 salários. Primeiro devemos montar o rol:
Rol = {1100, 1200, 1210, 1250, 1300, 1450, 1500, 1600, 1980}
Quando o número de elementos do conjunto de dados for ímpar, a mediana é o valor que divide o conjunto ao meio, portanto Md = 1300. Observe que à esquerda e à direita de 1300 existem 4 elementos.
2. Mediana de um conjunto de dados com número de elementos ímpar.
Considere o conjunto de dados abaixo, referente ao salário médio dos funcionários de uma empresa.
Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980 1420
Rol = { 1100, 1200, 1210, 1250, 1300, 1420, 1450, 1500, 1600, 1980}
Nesse conjunto existem 10 elementos. Nesse caso a mediana será a média aritmética dos dois valores centrais. Note que tanto à direita como à esquerda dos dois valores centrais há 4 elementos. Assim,
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Especialista em Estatística e Modelagem Matemática
Variância e desvio-padrão
A variância e o desvio-padrão são medidas de dispersão. Há situações em que as medidas de tendência central, como a média, a moda e a mediana, não são as mais adequadas para a análise de uma amostra de valores. Nesses casos, é necessário utilizar as medidas de dispersão.
Em um vestibular onde o critério de aprovação para a próxima fase é ficar acima da média de acertos dos candidatos, um determinado candidato só precisa comparar seu número de acertos com essa média para saber se passou para a próxima fase.
Para se ter uma ideia do tempo de viagem de uma determinada linha de ônibus, pode-se ter por base o tempo mais frequentemente observado, que seria a moda. Provavelmente, os resultados acima e abaixo desse valor mais frequente podem ter sido obtidos em dias mais atípicos, com mais congestionamento nas ruas, em finais de semana ou em um feriado.
Agora, considere uma escola que deseja ajudar alunos de uma turma com dificuldade em uma determinada matéria, por meio de um projeto específico de acompanhamento desses alunos. Sabendo somente que a média dos alunos dessa turma na referida matéria foi por volta de 6,0, ela não terá informações suficientes para fazer um projeto que atenda adequadamente os alunos com dificuldades. Nesse caso, interessa saber mais sobre os alunos que ficaram abaixo dessa média.
Considere que um grupo de alunos tenha tirado as seguintes notas em uma determinada matéria: 2,0; 3,0; 3,0; 4,0; 5,0; 6,0; 7,0; 8,0; 9,0; 10,0.
Para calcular essas medidas de dispersão, é útil conhecer a média desses valores:
Agora, calculamos os desvios de todas essas notas em relação à média:
Se calcularmos a média desses desvios, somando-os e dividindo o resultado por 10, ela será nula, pois a soma de todos esses desvios será zero, pelo próprio significado da média como medida de tendência central.
Assim, elevamos ao quadrado esses desvios e, aí sim, tiramos a média dos resultados. É a variância.
Podemos concluir que a dispersão das notas em relação à média é de 6,81.
No entanto, a variância não está na mesma unidade que as nossas notas, pois os desvios foram elevados ao quadrado. Para conservarmos as unidades do desvio e dos dados, calculamos o desvio-padrão, o qual nada mais é do que extrair a raiz quadrada da variância.
Logo, o desvio das notas em relação à média é de 2,61 pontos.
No nosso exemplo, com essa informação, é possível à escola ter uma idéia melhor da situação da turma e dos alunos que estão abaixo da média.
Em um vestibular onde o critério de aprovação para a próxima fase é ficar acima da média de acertos dos candidatos, um determinado candidato só precisa comparar seu número de acertos com essa média para saber se passou para a próxima fase.
Para se ter uma ideia do tempo de viagem de uma determinada linha de ônibus, pode-se ter por base o tempo mais frequentemente observado, que seria a moda. Provavelmente, os resultados acima e abaixo desse valor mais frequente podem ter sido obtidos em dias mais atípicos, com mais congestionamento nas ruas, em finais de semana ou em um feriado.
Agora, considere uma escola que deseja ajudar alunos de uma turma com dificuldade em uma determinada matéria, por meio de um projeto específico de acompanhamento desses alunos. Sabendo somente que a média dos alunos dessa turma na referida matéria foi por volta de 6,0, ela não terá informações suficientes para fazer um projeto que atenda adequadamente os alunos com dificuldades. Nesse caso, interessa saber mais sobre os alunos que ficaram abaixo dessa média.
Como calcular
Para situações como essa, as medidas de dispersão são muito úteis. Vamos nos basear nesse último exemplo para mostrar como se calcula a variância e o desvio-padrão.Considere que um grupo de alunos tenha tirado as seguintes notas em uma determinada matéria: 2,0; 3,0; 3,0; 4,0; 5,0; 6,0; 7,0; 8,0; 9,0; 10,0.
Para calcular essas medidas de dispersão, é útil conhecer a média desses valores:
 |
Agora, calculamos os desvios de todas essas notas em relação à média:
 |
Se calcularmos a média desses desvios, somando-os e dividindo o resultado por 10, ela será nula, pois a soma de todos esses desvios será zero, pelo próprio significado da média como medida de tendência central.
Assim, elevamos ao quadrado esses desvios e, aí sim, tiramos a média dos resultados. É a variância.
 |
 |
Podemos concluir que a dispersão das notas em relação à média é de 6,81.
No entanto, a variância não está na mesma unidade que as nossas notas, pois os desvios foram elevados ao quadrado. Para conservarmos as unidades do desvio e dos dados, calculamos o desvio-padrão, o qual nada mais é do que extrair a raiz quadrada da variância.
 |
Logo, o desvio das notas em relação à média é de 2,61 pontos.
No nosso exemplo, com essa informação, é possível à escola ter uma idéia melhor da situação da turma e dos alunos que estão abaixo da média.
*Michele Viana Debus de França é licenciada em matemática pela USP e mestre em educação matemática pela PUC-SP.
Assinar:
Comentários (Atom)
 clique aqui para efetuar o download dos dados utilizados nesse exemplo
clique aqui para efetuar o download dos dados utilizados nesse exemplo