Link para as Provas da OBMEP 2010

Se quiser abaixar as provas da 6º Olimpíada Brasileira de Matemática das Escolas Públicas, clique no link abaixo, elas estão com gabarito. Uma ótima oportunidade para estudar!!
http://www.obmep.org.br/

Questões da Olimpíada brasileira de Matemática

(OBM 2003 – 1ª Fase – Nível 1)
Um troféu formado por cinco recipientes cúbicos foi construído da seguinte maneira: sob o cubo de lado 10 cm foi soldado o cubo de lado 20 cm, sob este foi soldado o cubo de lado 30 cm, e assim por diante. Toda a superfície externa desse troféu deverá ser coberta com um certo tipo de revestimento. Quantos metros quadrados desse revestimento serão necessários?

A) 1,5
B) 2,5
C) 2,7
D) 2,75
E) 3
Resposta:

Juntando-se as partes das faces superiores dos cubos, obtemos uma face do cubo maior, de aresta 50 cm. A face inferior do cubo também é revestida. As quatro faces laterais dos cinco cubos deverão ser revestidas. Portanto, a área total é igual a

.

Resposta correta letra C.
(OBM 2006 – 1ª Fase – Nível 1)
Em um tanque há 4000 bolinhas de pingue-pongue. Um menino começou a retirar as bolinhas, uma por uma, com velocidade constante, quando eram 10h. Após 6 horas, havia no tanque 3520 bolinhas. Se o menino continuasse no mesmo ritmo, quando o tanque ficaria com 2000 bolinhas?
A) às 11h do dia seguinte
B) às 23h do mesmo dia
C) às 4h do dia seguinte
D) às 7h do dia seguinte
E) às 9h do dia seguinte
Resposta:
Em 6h de trabalho foram retiradas bolinhas e como a velocidade de retirada é constante, saem bolinhas por hora.
Para que 2000 bolinhas saiam do tanque são necessárias horas.

Portanto, o tanque ficou com 2000 bolinhas às 11h do dia seguinte.
Resposta correta letra A.
(OBM 2007 – 1ª Fase – Nível 1)
A soma de todos os números positivos ímpares até 2007 menos a soma de todos os números positivos pares até 2007 é igual a:
A) 1003
B) 1004
C) 2005
D) 2006
E) 2007
Resposta:
A soma de todos os números positivos ímpares até 2007 menos a soma dos números positivos pares até 2007 é (1 – 2) + (3 – 4) + (5 – 6) + ... + (2005 – 2006) + 2007 = –1003 + 2007 = 1004.
Resposta correta letra B.
Referência: www.obm.org.br e http://professoraju-mat.blogspot.com/

Matemática para concurso Banco do Brasil

Apostila Para Concursos

View more documents from porqueira.

Banco de questões da olimpiada de Matemática 2009

Bq2009 Final

View more documents from Antonio Carlos.

OBMEP provas

Provas obmep

Questões da Olimpíada brasileira de Matemática

(OBM 2005 – 1ª Fase – Nível 3)
Quantos números entre 10 e 13000, quando lidos da esquerda para a direita, são formados por dígitos consecutivos e em ordem crescente? Exemplificando, 456 é um desses números, mas 7890 não é:
A) 10
B) 13
C) 18
D) 22
E) 25
Resposta:
Os números em questão são 12, 23, 34, 45, …, 89 (8 números);
123, 234, 345, …, 789 (7 números);
1234, 2345, …, 6789 (6 números) e, por fim, 12345, um total de 8 + 7 + 6 + 1 = 22
números.
Resposta correta letra D.
(OBM 2008 – 1ª Fase – Nível 3)
Cinco inteiros positivos maiores que um satisfazem as seguintes condições:

Quanto vale a soma ?
A) 9
B) 16
C) 25
D) 36
E) 49
Resposta:
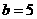
Se são cinco inteiros maiores que um, então , e com isso, a soma de quaisquer quatro deles é pelo menos 8. Observando a equação , onde 5 e 31 são primos, temos que e . Portanto,
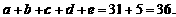
Obs.: Note que a = 4, b = 5, c = 7, d = 9 e e = 11 é solução do sistema.
Resposta correta letra D.
(OBM 2010 – 1ª Fase – Nível 3)
Quatro números inteiros positivos a < b < c < d são tais que o mdc entre quaisquer dois deles é maior do que 1, mas mdc(a, b, c, d) = 1. Qual é o menor valor possível para d?
A) 10
B) 12
C) 15
D) 30
E) 105
Resposta:
Nenhum dos inteiros em questão é uma potência de um primo p pois caso contrário todos os outros inteiros teriam o fator p em comum e isso não é permitido. Logo d possui pelo menos dois fatores primos distintos. Além disso, um dos números a, b, c, d é ímpar; caso contrário mdc (a, b, c, d) = 2. Assim, como o menor número ímpar com dois fatores primos distintos é 15,
Para d = 15, temos como exemplo a = 6, b = 10, c = 12 e d = 15.
Resposta correta letra C.
É isso aí.
Bons estudos, e qualquer dúvida, é só perguntar.
Abraços,
Ju

Questões da Olimpíada Brasileira de Matemática - Nível 2

terça-feira, 12 de abril de 2011

(OBM 2005 – 1ª Fase – Nível 2)
Devido a um defeito de impressão, um livro de 600 páginas apresenta em branco todas as páginas cujos números são múltiplos de 3 ou de 4. Quantas páginas estão impressas?
A) 100
B) 150
C) 250
D) 300
E) 430
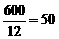
Resposta: Em 600 números inteiros consecutivos positivos, há múltiplos de 3 e múltiplos de 4; entretanto, alguns desses números aparecem duas vezes nessa contagem, pois são múltiplos dos dois números, ou seja, são múltiplos de 12. Como há desses múltiplos, concluímos que o número de páginas com defeito é .
Resposta correta letra D.
(OBM 2007 – 1ª Fase – Nível 2)
Observe as multiplicações a seguir:

Qual é a soma dos algarismos do número obtido quando multiplicamos 101 pelo número ?
A) 1001
B) 2007
C) 2009
D) 4008
E) 4014
Resposta: No resultado da multiplicação de 101 por , o dígito 1 aparece 4 vezes e o dígito 2 aparece 2007 – 4 = 2005 vezes. Portanto a soma dos algarismos desse número é .
Resposta correta letra E.
(OBM 2009 – 1ª Fase – Nível 2)
Para cada número natural n, seja a soma dos dez primeiros múltiplos positivos de n. Por exemplo, = 2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 + 20. Quanto é ?
A) 2925
B) 3025
C) 3125
D) 3225
E) 3325
Resposta:




Logo,
Resposta correta letra B.
fonte: http://professoraju-mat.blogspot.com