Questões da Olimpíada brasileira de Matemática

(OBM 2005 – 1ª Fase – Nível 3)
Quantos números entre 10 e 13000, quando lidos da esquerda para a direita, são formados por dígitos consecutivos e em ordem crescente? Exemplificando, 456 é um desses números, mas 7890 não é:
A) 10
B) 13
C) 18
D) 22
E) 25
Resposta:
Os números em questão são 12, 23, 34, 45, …, 89 (8 números);
123, 234, 345, …, 789 (7 números);
1234, 2345, …, 6789 (6 números) e, por fim, 12345, um total de 8 + 7 + 6 + 1 = 22
números.
Resposta correta letra D.
(OBM 2008 – 1ª Fase – Nível 3)
Cinco inteiros positivos maiores que um satisfazem as seguintes condições:

Quanto vale a soma ?
A) 9
B) 16
C) 25
D) 36
E) 49
Resposta:
Se são cinco inteiros maiores que um, então , e com isso, a soma de quaisquer quatro deles é pelo menos 8. Observando a equação , onde 5 e 31 são primos, temos qu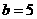e e . Portanto,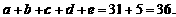
Obs.: Note que a = 4, b = 5, c = 7, d = 9 e e = 11 é solução do sistema.
Resposta correta letra D.
(OBM 2010 – 1ª Fase – Nível 3)
Quatro números inteiros positivos a < b < c < d são tais que o mdc entre quaisquer dois deles é maior do que 1, mas mdc(a, b, c, d) = 1. Qual é o menor valor possível para d?
A) 10
B) 12
C) 15
D) 30
E) 105
Resposta:
Nenhum dos inteiros em questão é uma potência de um primo p pois caso contrário todos os outros inteiros teriam o fator p em comum e isso não é permitido. Logo d possui pelo menos dois fatores primos distintos. Além disso, um dos números a, b, c, d é ímpar; caso contrário mdc (a, b, c, d) = 2. Assim, como o menor número ímpar com dois fatores primos distintos é 15,
Para d = 15, temos como exemplo a = 6, b = 10, c = 12 e d = 15.
Resposta correta letra C.
É isso aí.
Bons estudos, e qualquer dúvida, é só perguntar.
Abraços,
Ju

Questões da Olimpíada Brasileira de Matemática - Nível 2

terça-feira, 12 de abril de 2011

(OBM 2005 – 1ª Fase – Nível 2)
Devido a um defeito de impressão, um livro de 600 páginas apresenta em branco todas as páginas cujos números são múltiplos de 3 ou de 4. Quantas páginas estão impressas?
A) 100
B) 150
C) 250
D) 300
E) 430
Resposta: Em 600 números inteiros consecutivos positivos, há múltiplos de 3 e múltiplos de 4; entretanto, alguns desses números aparecem duas vezes nessa contagem, pois são múltiplos dos dois números, ou seja, são múltiplos de 12. Como há desses múltiplos, concluímos que o número de páginas com defeito é .
Resposta correta letra D.
(OBM 2007 – 1ª Fase – Nível 2)
Observe as multiplicações a seguir:

Qual é a soma dos algarismos do número obtido quando multiplicamos 101 pelo número ?
A) 1001
B) 2007
C) 2009
D) 4008
E) 4014
Resposta: No resultado da multiplicação de 101 por , o dígito 1 aparece 4 vezes e o dígito 2 aparece 2007 – 4 = 2005 vezes. Portanto a soma dos algarismos desse número é .
Resposta correta letra E.
(OBM 2009 – 1ª Fase – Nível 2)
Para cada número natural n, seja a soma dos dez primeiros múltiplos positivos de n. Por exemplo, = 2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 + 20. Quanto é ?
A) 2925
B) 3025
C) 3125
D) 3225
E) 3325
Resposta:




Logo,
Resposta correta letra B.
fonte: http://professoraju-mat.blogspot.com