Moda e mediana

Ao realizar uma pesquisa é aconselhável realizar um estudo estatístico dos dados apresentados. Através desse estudo podemos tirar as conclusões necessárias sobre o universo pesquisado. A estatística descritiva é a parte da estatística responsável por realizar essa análise, apontando tendências de comportamento das variáveis, criando gráficos e descrevendo as características dos conjuntos pesquisados.

Numa pesquisa, os dados tendem a se concentrar em torno dos valores centrais. Esses valores centrais são chamados de medidas de tendência central. São elas: Média, Moda e Mediana. Iremos abordar e conceituar Moda e Mediana.

Definição de Moda (M_o): é o valor que mais aparece num conjunto de dados.

Exemplo 1. Os dados abaixo se referem à idade de 20 alunos de uma turma de 6º ano.

Idade: {12, 11, 12, 13, 12, 11, 13, 12, 12, 11, 14, 13, 13, 12, 11, 12, 13, 14, 11, 14}

A moda desse conjunto de dados será a idade que mais aparece, ou seja:

M_o = 12 (pois é a idade que aparece mais vezes no conjunto)

Exemplo 2. A tabela abaixo apresenta as notas em matemática de uma turma de 30 alunos.

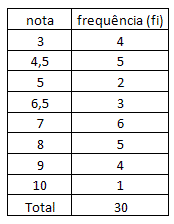
Na coluna da esquerda temos as notas na disciplina de matemática e na coluna da direita, quantos alunos obtiveram a respectiva nota. Dessa forma, podemos observar que a nota que mais aparece nesse conjunto de dados é 7. Portanto,
M_o = 7.

Exemplo 3. Os dados abaixo são referentes ao número dos calçados vendidos em uma loja num determinado dia.

{35, 33, 36, 35, 37, 36, 39, 40, 42, 43, 35, 36, 42}
Nesse caso, existem dois números de sapatos que aparecem mais vezes: 35 e 36. Logo, a moda pode ser:
M_o = 35 ou M_o = 36
Quando isso ocorre, dizemos que o conjunto de dados é bimodal.

Definição de Mediana (M_d): é o valor (pertencente ou não ao conjunto de dados) que divide o conjunto de dados em dois subconjuntos de mesmo tamanho. De uma forma mais simples, é o valor que divide o conjunto de dados ao meio.

Para determinar a mediana de um conjunto de dados é necessário, primeiro, construir o rol. O rol é a ordenação do conjunto de dados em ordem crescente ou decrescente.

1. Mediana de um conjunto de dados com número de elementos ímpar.

Considere o conjunto de dados abaixo, referentes ao salário médio dos funcionários de uma empresa em reais.
Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980

Observe que nesse conjunto de dados temos 9 elementos, 9 salários. Primeiro devemos montar o rol:
Rol = {1100, 1200, 1210, 1250, 1300, 1450, 1500, 1600, 1980}

Quando o número de elementos do conjunto de dados for ímpar, a mediana é o valor que divide o conjunto ao meio, portanto M_d = 1300. Observe que à esquerda e à direita de 1300 existem 4 elementos.

2. Mediana de um conjunto de dados com número de elementos ímpar.

Considere o conjunto de dados abaixo, referente ao salário médio dos funcionários de uma empresa.
Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980 1420

Rol = { 1100, 1200, 1210, 1250, 1300, 1420, 1450, 1500, 1600, 1980}

Nesse conjunto existem 10 elementos. Nesse caso a mediana será a média aritmética dos dois valores centrais. Note que tanto à direita como à esquerda dos dois valores centrais há 4 elementos. Assim,

Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática