Professor de Matemática no Colégio Estadual Dinah Gonçalves
E Biologia na rede privada de Salvador-Bahia
Professor Antonio Carlos carneiro Barroso
email accbarroso@hotmail.com
http://accbarrosogestar.blogspot.com.br
Cubo da soma e cubo da diferença
Por Marcelo Rigonatto
Calculo de produtos notáveis
Cubo da soma
Sejam a e b números reais diferentes de zero. Temos que:
(a + b)3 = (a + b)2(a + b) = (a2 + 2ab + b2)(a + b) = a3 + 2a2b +ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3.
Observe que utilizamos o quadrado da soma, que é outro produto notável, para obter o cubo da soma. De uma forma geral, o cubo da soma pode ser obtido da seguinte maneira:
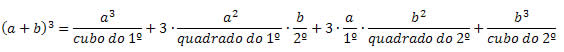
Cubo da diferença
O cubo da diferença é feito de maneira análoga ao cubo da soma. Observe:
(a – b)3 = (a – b)2(a – b) = (a2 – 2ab + b2)(a – b) = a3 – 3a2b + 3ab2 – b3
De uma forma geral, temos:
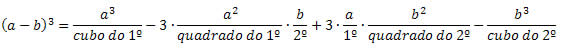
Vejamos alguns exemplos para melhor esclarecimento.
Exemplo 1. Desenvolva os seguintes produtos notáveis.
Solução:
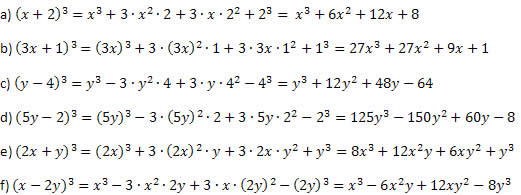
Procedendo como foi explicado antes do exemplo e tendo o cuidado ao realizar as potências e a multiplicações, não há como errar. O procedimento é sempre o mesmo para o cubo da soma e para o cubo da diferença, diferindo somente o sinal do segundo membro e do último.
Exemplo 2. Simplifique a expressão abaixo.
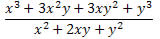
Solução: Observe que no numerador e no denominador da fração aparecem dois produtos notáveis. No numerador há um cubo da soma de dois termos que foi desenvolvido e no denominador, um quadrado da soma de dois termos. Assim, podemos reescrevê-los da seguinte forma:
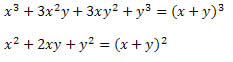
Logo, a expressão pode ser escrita como:
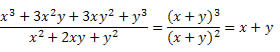
Para chegar ao resultado utilizamos a propriedade da divisão de potências de bases iguais (conserva a base e subtrai os expoentes).
Exemplo 3. Desenvolva o seguinte produto notável
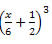
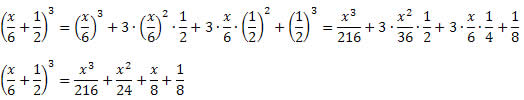
Nenhum comentário:
Postar um comentário