Potenciação e Radiciação

Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso

Colégio Estadual Dinah Gonçalves www.accbarrosogestar.wordpress.com

email accbarroso@hotmail.com

Blog HTTP://ensinodematemtica.blogspot.com

Teste de Conhecimento em Potenciação e Radiciação

• Cada pergunta vale um ponto e resposta errada não anula resposta certa. Boa Sorte!
• (FATEC) Das três sentenças abaixo:A) 2^x+3 = 2^x.2³
  B) (25)^x = 5^2x
  C) 2^x + 3^x = 5^x
  
  • 
    Para responder a questão é necessário analisar individualmente cada uma das três sentenças dadas.
    A) É verdadeira em decorrência da propriedade do produto de potências de mesma base: conserva-se a base e somam-se os expoentes;
    B) Podemos escrever como:
    
    (25)^x = (5²)^x = 5^2x
    Na passagem para a segunda igualdade foi utilizada a propriedade: A potência n da potência m de um número relativo a é igual a potência de a cujo expoente é o produto dos expoentes m e n.
    Logo B) também é verdadeira.
    C) A sentença é obviamente falsa, pois na soma de potências não é viável estabelecer qualquer regra. Para calcular soma de potências é necessário efetuar o cálculo de cada parcela e após somá-las.
    No entanto, observe que a sentença é verdadeira para x = 1. Mas, por exemplo, para x = 2 a igualdade não ocorre:
    
    2² + 3² = 4 + 9 = 13 e 5² = 25
    E portanto, concluímos que a resposta correta é: Somente a sentença C) é falsa.
• O valor da expressão:
  
  é:
  
  • 
    Da propriedade "a raiz de índice m de uma raiz de índice n de a é igual à raiz de índice mn de a", cuja demonstração foi feita no post Exercícios Resolvidos #3 - Radiciação, Exercício 1, obtemos:
    
    
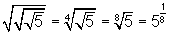
    Na última iguldade foi utilizada a seguinte propriedade: "A raiz de índice n da potência de grau m de a é igual à potência de grau m/n de a", com a = 5, m = 1 e n = 8.
• (GV-SP) A expressão (1/2)^-3 + (1/2)^-5 é igual a:
  • 
    A solução do exercício é consequência direta do uso da propriedade da potenciação a^-m = 1/a^m e da divisão de frações:
    
    (1/2)^-3 + (1/2)^-5 = 1/(1/2)³ + 1/(1/2)⁵ = 1/(1/2³) + 1/(1/2⁵) =>
    (1/2)^-3 + (1/2)^-5 = 1.(2³/1) + 1.(2⁵/1) = 2³ + 2⁵ = 8 + 32 = 40
• Determine o valor da expressão:
  
  
  • 
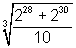
    Observe que o numerador da fração pode ser escrito como:
    
    2²⁸ + 2³⁰ = 2²⁸ + 2²⁸.2²
    Colocando o termo comum às duas parcelas em evidência vem:
    
    2²⁸ + 2³⁰ = 2²⁸(1 + 2²) = 2²⁸.5
    Substituindo o valor na fração:
    
    (2²⁸ + 2³⁰)/10 = 2²⁸.5/10 = 2²⁸/2 = 2²⁷
    E, finalmente, extraindo a raiz cúbica de 2²⁷ obtemos que o valor da expressão é:
    
    2⁹
• (SANTA CASA - SP) O valor de (3^-1 + 5^-1)/2^-1 é:
  • 
    Mais uma vez vamos utilizar a propriedade da potenciação a^-m = 1/a^m e de operações com fações para obter o resultado do exercício:
    
    E = (3^-1 + 5^-1)/2^-1 = (1/3 + 1/5)/(1/2)
    Determinando o mmc dos denominadores das frações 1/3 e 1/5, que é igual a 15, e somando essas frações:
    
    E = [(5 + 3)/15]/(1/2) = (8/15)/(1/2)
    Para concluir basta utilizar a propriedade da divisão de frações "conserva-se a primeira e multiplica-se pelo inverso da segunda":
    
    E = (8/15).(2/1) = 16/15
• Simplificar o radical
  
  
  • 
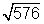
    Inicialmente fatore 576, ou seja transforme 576 no produto de potências, cujas bases são números primos:
    
    576 | 2
    288 | 2
    144 | 2
    072 | 2
    036 | 2
    018 | 2
    009 | 3
    003 | 3
    001 | 1
    Do procedimento acima vem, então, que:
    
    √576 = √2⁶.3² = √2⁶.√3² = 2³.3 = 24
    Nas passagens das igualdades acima foram utilizadas as seguintes propriedades:
    • A raiz enésima do produto a.b é igual ao produto das raízes enésimas de a e b. Na solução: n = 2, a = 2⁶ e b = 3²;
    • A raiz enésima de a elevado a m é igual a raiz de índice n/p de a elevado a m/p obtida dividindo-se o índice e o radicando por p. Na solução acima foi utilizada a propriedade para n =2, p = 2 e m = 6 no primeiro fator e m = 2 no segundo.
• Se n é um número inteiro e a é um número real positivo simplifique a expressão a²ⁿ⁺¹.a^1-n.a^3-n
  • 
    A solução da questão é bem simples e é feita pela aplicação direta da seguinte propriedade: no produto de potências de mesma base, conserva-se a base e soma-se os expoentes.
    Logo:
    
    a²ⁿ⁺¹.a^1-n.a^3-n = a^2n+1+1-n+3-n = a⁵
• Efetue a operação
  
  
  • 
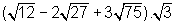
    Reescrevendo cada radical da expressão entre parênteses, onde são utilizados a fatoração dos radicandos e a propriedade da raiz de um produto, obtemos:
    
    
    
    Agora, substituindo os valores obtidos na expressão:
    
    
• (PUC - SP) O produto a^m.a^m é igual a:
  • 
    Mais um exercício simples que visa fixar a propriedade do produto de potências de mesma base, e portanto, de rápida e fácil solução:
    
    a^m.a^m = a^m+m = a^2m
• (UMC - SP) Seja
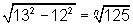
  O valor de n é:
  
  • 
    Calculemos primeiro o valor da expressão do lado esquerdo da igualdade:
    
    Substituindo o valor obtido na igualdade dada, temos:
    
    De [1] vem pela definição de radiciação que:
    
    em decorrência do fato de que potências iguais de mesma base têm necessariamente os expoentes iguais.
  • http://www.nghorta.com