Determinantes: Regra de Sarrus

Pierre Frederic SARRUS (1798 - 1861), foi professor na universidade francesa de Strasbourg. São escassas, e eu diria, inexistentes, as informaçoes sobre o Prof. SARRUS nos livros de Matemática do segundo Grau, que Apresentamo (ou mais simplesmente apenas citam) o nome do professor, na forma REGRA DE SARRUS, para o cálculo dos determinantes de terceira Ordem.

A regra de SARRUS, foi provávelmente escrita no ano de 1833. O Prof. SARRUS, foi premiado Pela Academia Francesa de Ciências, Pela autoria de UM trabalho que versava sobre as integrais múltiplas.

Cálculo do determinante de 3ª Ordem através da Regra de Sarrus .

Este cálculo pode ser feito da seguinte maneira:

Acompanhe como aplicamos Essa regra para .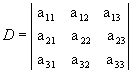

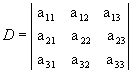1º Passo : Repetimos as duas primeiras colunas do lado da terceira:

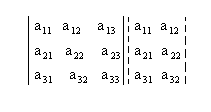
2º Passo : Encontramos a soma do produto dos elementos da diagonal principal com os Dois produtos obtidos Pela multiplicação dos elementos das paralelas a Essa diagonal (a soma Deve ser precedida do sinal positivo):

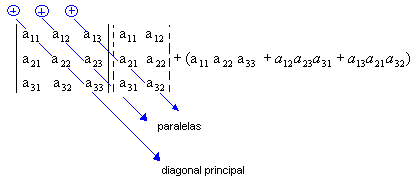
3º Passo : Encontramos a soma do produto dos elementos da diagonal secundária com os Dois produtos obtidos Pela multiplicação dos elementos das paralelas a Essa diagonal (a soma Deve ser precedida do sinal negativo):

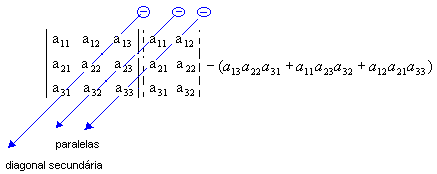
Assim:

Observação: Se desenvolvermos ESSE determinante 3ª Ordem aplicando o Teorema de Laplace, encontraremos o mesmo número real.

Determinante de Ordem n> 3

Vimos que a regra de Sarrus é válida para o cálculo do determinante de umha matriz de Ordem 3. Quand a matriz é de Ordem superior a 3, devemos usar o Teorema de Laplace para chegar a determinantes de Ordem 3 e depois aplicar a regra de Sarrus .

Referência:

Site: Algo Sobre Vestibular.

Site: Só Matemática.