Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
A estrutura atômica da matéria
Estatueta de bronze da idade dos Metais, por volta de 3000 aC.
|
Desde a antiguidade o ser humano vem investigando para saber mais sobre a matéria e usar esse conhecimento para viver melhor. Uma curiosidade muita antiga é esta:
Tudo o que existe é feito de matéria, mas de que é feita a matéria?
Pelos registros que temos até hoje, as respostas mais antigas obtidas pela humanidade para as questões colocadas na página anterior tiveram por base a religião e a mitologia.
No entanto, essas explicações não atendiam às necessidades práticas das sociedades da época. Não forneciam, por exemplo, o conhecimento que se fazia necessário à metalurgia e, mais tarde, à siderurgia.
Há milhares de anos, o ser humano é capaz de misturar alguns materiais e, com isso, obter outros materiais, diferentes dos animais. Um exemplo é a liga de bronze – mistura dos metais cobre e estanho, que já era produzida há 5000 anos.
|
Com esses avanços, outras questões surgiram:
- Porque alguns tipos de material, ao se misturarem se transforma em outro material?
- Como ocorrem essas transformações?
Para explicar essas e outras questões práticas, surgiu a necessidade de saber de que é feita a matéria ou de que é constituída a menor partícula de água, do ferro e de tudo o que existe.
Os escritos mais antigos que contêm explicações sobre a estrutura da matéria pertencem aos filósofos gregos do século V antes de Cristo.
Há cerca de 2500 anos, os filósofos gregos Leucipo e Demócrito indagavam sobre a estrutura fundamental da matéria. Eles afirmaram que a água, então tida como um elemento fundamental de tudo o que existe, era composta por partículas indivisíveis que receberam o nome de átomos. A palavra átomo significa, em grego, “indivisível”.
Todo e qualquer tipo de matéria existente no Universo seria constituído de átomos. Os diversos materiais teriam em sua constituição átomos diferentes, e esses átomos estariam em diferentes proporções.
Essa idéia de átomo – partícula indivisível da matéria – foi aceita sem alterações significativas por mais de 2 000 anos.
Os modelos atômicos
Como explicar o que é invisível? Apesar de todos os sofisticados aparelhos empregados nas investigações e das avançadas pesquisas sobre o átomo, ele continua invisível.
O estudo do átomo é realizado a partir de modelos idealizados pelos cientistas, isto é, representações hipotéticas da idéias que se tem de como é e de que é formado o átomo.
O conceito de átomo indivisível, imutável e indestrutível afirmado pelos sábios gregos era uma idéia filosófica.
Da idéia filosófica à primeira explicação científica sobre o átomo transcorreram mais de vinte séculos.
Foi no século XIX, com o início da Revolução industrial, que o conhecimento científico ganhou maior importância. Nesse século, intensificou-se o interesse pelo conhecimento que possibilitasse realizar a transformação de um material em outro. Os cientistas ainda buscavam conhecer uma forma de transformar elementos minerais comuns, como o ferro, por exemplo, em elementos nobres e raros, como ouro e prata.
Teoria atômica de Dalton
Em 1808, o químico inglês John Dalton retomou a hipótese atômica de Demócrito para explicar a composição da matéria.
 |
Por meio de vários experimentos, Dalton concluiu que algumas substâncias são formadas por outros elementos. Por exemplo: o hidrogênio e o oxigênio são substâncias que se combinam para formar a substância água.
Segundo Dalton, nas diversas combinações dos átomos – ainda tidos como partículas fundamentais e indivisíveis – estaria a origem da diversidade das substâncias conhecidas.
|  |
Portador da cegueira específica para determinadas cores, estudou essa anomalia que recebeu o nome de daltonismo, em sua homenagem.
O modelo de Thomson
 |
O modelo de Dalton possibilitou explicação de diversos fenômenos e contribuiu muito para a evolução do conhecimento da matéria. No entanto, não considerava a natureza elétrica da matéria.
A eletricidade era estudada desde o século XVIII, e os cientistas avançavam em novas pesquisas e experimentos. A teoria referente à existência de uma partícula da matéria de carga negativa, o elétron, se consolidava.
Novos conhecimentos, novas questões eram formuladas, e o modelo de Dalton não satisfazia, pois não explicava a existência do elétron. Era necessário, então, um modelo que tivesse como base o fato de a matéria, portanto o átomo, possuir partículas com a carga elétrica negativa e, supostamente, também conter partículas com carga elétrica positiva.
|
Cerca de um século depois de Dalton, o cientista inglês Joseph John Thomson propôs outro modelo para explicar o átomo, levando em consideração o conhecimento já existente sobre eletricidade.
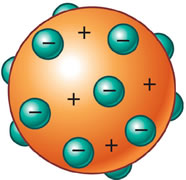
Em 1887, Thomson afirmou que o átomo seria uma esfera neutra, maciça e não-homogênia, composta por um fluído positivo onde estariam dispersos os elétrons.
No modelo de Thomson, o átomo continua sendo representado por uma minúscula esfera maciça, porém revela o átomo como uma estrutura complexa e divisível.
Esse modelo de átomo á chamado por alguns de “pudim de passas”: a massa do pudim seria a carga positiva, e as passas espalhadas sobre o pudim seriam as partículas negativas – os elétrons.
A descoberta e os estudos de radioatividade, além dos significativos avanços tecnológicos, levaram os cientistas a novas especulações sobre a composição da matéria e a estrutura do átomo.
O Modelo de Rutherford
Em 1904, o cientista neozelandês Ernest Rutherford realizou um experimento que ficou conhecido na história da ciência como experimento de Rutherford. Ele já sabia da existência das partículas de carga positiva, denominadas partículas alfa (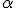
). Em seu experimento, Rutherford colocou no interior de um bloco de chumbo uma substância emissora de partículas 
, de forma que elas fossem orientadas, por meio de um orifício em uma placa de chumbo, a colidir contra uma fina lâmina de ouro.
). Em seu experimento, Rutherford colocou no interior de um bloco de chumbo uma substância emissora de partículas 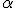, de forma que elas fossem orientadas, por meio de um orifício em uma placa de chumbo, a colidir contra uma fina lâmina de ouro.
Observe o esquema do experimento de Rutherford:
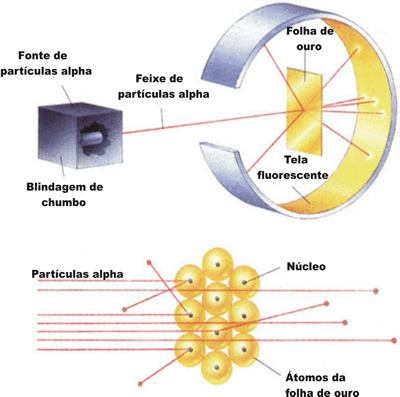
Com esse experimento, ele verificou que:
- a maioria das partículas
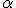atravessa a lâmina de ouro; - algumas dessas partículas, ao atravessar a lâmina, eram desviadas;
- uma pequena parte das partículas
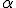não ultrapassa a lâmina e retornava, como se essas partículas se chocassem com algo muito denso.
Analisando esses resultados, Rutherford concluiu que:
- O átomo não é uma esfera maciça. Existem grandes espaços vazios visto que a maior parte das partículas
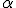atravessou a lâmina de ouro. - O átomo possui uma região central onde está concentrada a sua massa. Foi contra essa região, denominada por ele de núcleo, que as partículas
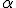, se chocaram e retornaram. - Esse núcleo apresenta carga positiva, pois repeliu a partícula
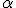- que também possui carga positiva.
Com esses dados, Rutherford construiu um modelo atômico semelhante ao Sistema Solar, em que o átomo é uma partícula muitíssimo pequena composta de duas regiões:
- uma interna, o núcleo, onde estariam concentradas praticamente toda a massa do átomo – de carga elétrica positiva, representada por partículas chamadas de prótons;
- outra externa, de massa desprezível, onde estariam os elétrons, diminutas partículas negativas em movimento ao redor do núcleo.
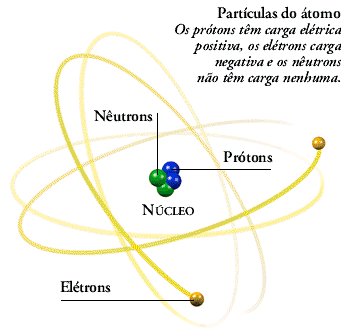
Nos modelos aqui apresentados, as dimensões do núcleo e da eletrosfera não estão em escala. Na realidade, a eletrosfera tem o seu volume cerca de 100 mil vezes maior que o do núcleo.
Em 1932, o físico inglês James Chadwick (1891-1974), realizando experiências com material radioativo, comprovou uma das hipóteses de Rutherford que afirmava a possibilidade de existir no núcleo uma outra partícula desprovida de carga elétrica.
Chadwick chamou essas partículas de nêutrons.
O modelo de Rutherford-Böhr
O modelo atômico de Rutherford foi complementado com um novo conceito introduzido pelo físico dinamarquês Niels Bohr:
“O elétrons descreve uma órbita circular ao redor do núcleo sem ganhar ou perder energia.”
Cada órbita descrita pelo elétron é denominada nível de energia ou camada de energia. Em um átomo, há várias órbitas circulares, cada uma delas com um determinado valor energético.
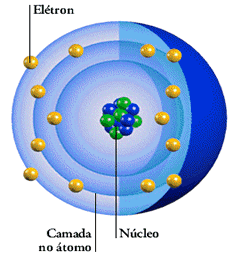
Outros modelos que vieram depois especificam as características das órbitas ou camadas de energia, incorporando a discussão de elétron considerado como partícula e/ou onda.
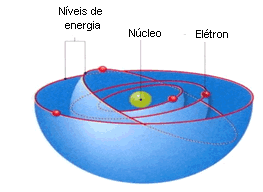
Pesquisas mais recentes, realizadas após a elaboração do modelo de Rutherford-Böhr, comprovaram que impossível determinar num mesmo instante a posição e a velocidade de um elétron. Por isso, cientistas afirmam que existe a probabilidade de os elétrons estarem em uma ou outra região da eletrosfera.
O Interior do Átomo
No centro de um átomo está o seu núcleo, que apesar de pequeno, contém quase toda a massa do átomo. Os prótons e os nêutrons são as partículas nele encontradas, cada um com uma massa atômica unitária.
O Número de prótons no núcleo estabelece o número atômico do elemento químico e, o número de prótons somado ao número de nêutrons é o número de massa atômica. Os elétrons ficam fora do núcleo e tem pequena massa.
Características das Partículas:
- Prótons: tem carga elétrica positiva e uma massa unitária.
- Nêutrons: não tem carga elétrica, mas tem massa unitária.
- Elétrons: tem carga elétrica negativa e quase não possuem massa.
Cargas elétricas e massas
Inúmeros experimentos realizados permitiram estabelecer as propriedades das partículas do átomo quanto à sua carga elétrica e massa.
Quando à carga elétrica: considera-se a carga do próton igual a +1; a carga do elétron igual a -1, e a carga do nêutron igual a 0.
Como se sabe, cargas elétricas de mesma intensidade e de sinais contrários se neutralizam. Ou seja, a carga elétrica de um próton (positiva) anula a carga elétrica de um elétron (negativa). Qualquer átomo apresenta número de prótons e de elétrons iguais; logo, é eletricamente neutro.
Quanto a massa: tendo o valor da massa do próton como referência, afirma-se que a massa do nêutron é praticamente igual à massa do próton. Como o próton possui massa cerca de 2 mil vezes maior que a de um elétron, esta última é considerada desprezível.
O núcleo do átomo
Agora, vamos considerar melhor as características do núcleo atômico.
Número atômico
Há muitos átomos diferentes entre si. Por exemplo, o átomo de alumínio é diferente do átomo de ouro. Qual será a principal diferença entre os tipos de átomos?
Após estudos definiu-se que o número de prótons é uma das principais características que diferenciam um átomo do outro.
Esse número é chamado de número atômico e é representado pela letra Z.
- Z é a “carteira de identidade” do átomo, pois indica a qual elemento químico cada átomo pertence.
- O conjunto dos átomos que possuem o mesmo número atômico (Z) é denominado elemento químico.
Portanto, a partir do conceito de elemento químico, á possível afirmar que átomos com número de prótons diferentes entre si pertencem, obrigatoriamente a elementos químicos diferentes. Vejamos:
O átomo de sódio tem 11 prótons; logo, seu número atômico é igual a 11 (Z = 11), e todos os átomos com número atômico (Z) igual a 11 pertencem ao elemento químico sódio.
Número de massa
É a soma do número de prótons com o número de nêutrons. O número de massa é representado pela letra A.
Nesta expressão, temos: A = número de massa;
p = número de prótons;
n = número de nêutrons.
Logo, a diferença entre o número de massa e o número atômico revela o número de nêutrons.
A soma do número de prótons com o número de nêutrons, ou seja, o número de massa (A), não corresponde a toda a massa do átomo, pois também existem os elétrons. O motivo de A representar a massa do átomo é que a amassa do elétron é desprezível quando comparada com a dos prótons e nêutrons.
Átomos pertencentes ao mesmo elemento químico podem apresentar diferentes números de nêutrons. A prata, por exemplo, é encontrada na natureza com números de nêutrons distintos: 60 e 62. Se somarmos esses números com o número de prótons, que é igual a 47, teremos:
- 60 nêutrons + 47 prótons = 107 como número de massa.
- 62 nêutrons + 47 prótons = 109 como número de massa.
Por isso, somente o número atômico pode identificar a que elemento químico o átomo pertence.
Representação dos átomos
Os átomos dos elementos químicos são representados por símbolos composto por uma, duas ou três letras. Para o sódio, utiliza-se Na, para o cloro Cl; para o carbono, C; e assim por diante.
Note que a primeira letra é sempre maiúscula. Normalmente, o número de massa (A) é representado no canto superior esquerdo, e o número atômico (Z) no canto inferior esquerdo.
Observe o exemplo para o elemento químico cloro:
Semelhanças atômicas
Além da existência de vários átomos com o mesmo número de prótons, pesquisas indicam que semelhanças podem ocorrer também com o número de nêutrons e com o número de massa.
Os átomos que possuem algum tipo de semelhança são agrupados em três grupos básicos: isótopos, isótonos e isóbaros.
Átomos isótopos são aqueles que apresentam o mesmo número de prótons e diferente número de nêutrons e de massa. Obrigatoriamente, pertencem ao mesmo elemento químico.
Exemplo:
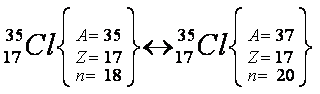
Átomos isótonos são aqueles que apresentam o mesmo número de nêutrons e diferente número de prótons e de massa. Obrigatoriamente, não podem pertencer ao mesmo elemento químico.
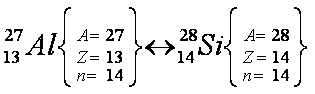
Átomos isóbaros são aqueles que apresentam o mesmo número de massa e diferente número de prótons e de nêutrons. Obrigatoriamente, não podem pertencer ao mesmo elemento químico.
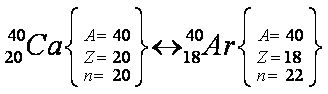
Eletrosfera e níveis energéticos
 |
Como vimos anteriormente, Bohr aperfeiçoou o modelo atômico de Rutherford com base em formulações teóricas. Uma delas é esta:
Os elétrons estão distribuídos de acordo com suas distâncias em relação ao núcleo, descrevendo órbitas circulares ao redor deste sem ganhar ou perder energia.
Assim, há várias órbitas circulares em um átomo, e cada uma delas tem um determinado valor energético. Dependendo do número de elétrons que possui, o átomo pode apresentar vários níveis eletrônicos ou camadas de energia.
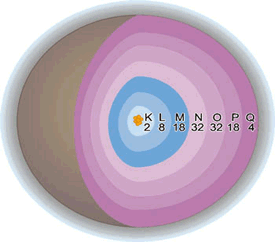
Esses níveis eletrônicos, conforme o número de elementos químicos conhecidos, são numerados de 1 a 7 ou representados pelas letras K, L, M, N, O, P e Q, a partir do nível mais interno, que é o mais próximo do núcleo.
|
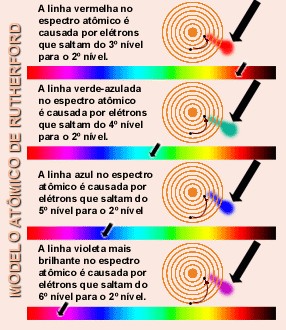
Bohr afirmou também que:
Ao receber energia o elétron pode saltar da camada em que está para uma camada mais externa; quando cessa a fonte de energia, ela retorna para a camada de origem, liberando sob a forma de luz a energia anteriormente recebida.
Pela observação das fotos seguir, você verá que a chama apresenta cores diferentes.
 |  |  |
|---|
O que se pode constatar ao observar as diferentes cores apresentadas nas fotos?
Isso ocorre porque os elétrons dos diferentes elementos químicos atingem camadas externas também diferentes ao ganhar energia. A emissão da luz depende da diferença de energia entre a camada eletrônica em que o se encontrava e a camada para a qual “saltou” ao receber energia.
A energia em forma de luz é emitida quando o elétron retorna à sua camada eletrônica inicial, e a cor da luz dependerá de cada elemento químico.
Como a luz visível é formada por ondas eletromagnéticas distribuídas numa certa faixa de frequências, e a frequências da onda corresponde a quantidade de energia que ela transporta, temos que, a energia emitida pelo elétron é percebida por nós na forma de luz com a cor determinada pela quantidade de energia liberada.
Isso explica, por exemplo, as cores dos fogos de artifício, já que eles são produzidos com adição de substâncias que emitem luz quando aquecidas.
Como vimos, de acordo com a teoria de Bohr, ao receber energia um elétron pode saltar para uma camada mais externa, de maior energia.
Atualmente, sabemos que, se a quantidade de energia fornecida a um elétron for muito elevada, esse elétron poderá saltar para fora da área considerada eletrosfera. Em conseqüência, o átomo deixa de apresentar igual número de prótons e elétrons, deixando, portanto de ser neutro.
|  |
Da mesma forma que se podem perder elétrons, o átomo também pode receber elétrons, ocorrendo a quebra de neutralidade de cargas elétricas.
Nos dois exemplos anteriores, foi possível verificar que, com a perda ou com o ganho de elétrons, os átomos deixaram de apresentar carga neutra. Quando isso ocorre, o átomo recebe uma nova denominação: são chamados de íons.
Os íons
Observe que, se um átomo perder um elétron, seu numero de prótons fica maior que o número de elétrons. Assim, o átomo assume uma carga positiva, transformando-se em um íon positivo, denominado cátion.
Considere novamente o átomo de sódio:
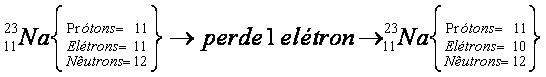
Quando o átomo de sódio perde um elétron, ele se transforma em um íon de carga positiva (+1). Caso o processo seja inverso, ou seja, o átomo receba um elétron, o número de elétrons torna-se superior ao de prótons e o átomo assume uma carga negativa, transformando-se em íon negativo, denominado ânion.
Agora, observe o átomo de cloro:
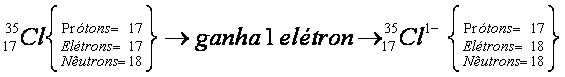
Nesse exemplo, a carga do íon cloro passa a valer -1, pois seu átomo de origem recebeu um elétron.
A quantidade de carga de um cátion ou ânion pode variar de acordo com o número de elétrons que o átomo de origem perdeu ou recebeu. Assim, é possível verificar a existência de íons com carga +1, -1, +2, -2, +3, -3 etc.
Veja um exemplo, considerando o átomo de magnésio:
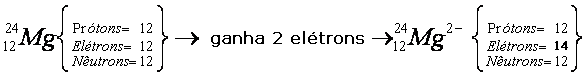
www.sobiologia.com.br
