A parte da Matemática responsável pelo agrupamento de elementos é denominada Análise Combinatória. Ao realizar agrupamentos de elementos devemos analisar as condições determinadas. Por exemplo, em algumas situações não devem ocorrer a presença de termos repetidos, e em outros casos, essa restrição não é imposta. Esse tipo de agrupamento é resolvido através do princípio multiplicativo, que consiste na multiplicação das possibilidades de cada posicionamento.
Exemplo 1
Utilizando os algarismos 1, 2, 3, 4 e 5, forme números de 3 algarismos, respeitando as seguintes condições:
a) os números podem ser repetidos
centenas dezenas unidades
5 5 5
Podemos utilizar 5 possibilidades na casa das centenas, 5 na casa das dezenas e 5 na casa das unidades.
5 * 5 * 5 = 125 números
b) Números distintos
centenas dezenas unidades
5 4 3
Utilizaremos 5 possibilidades na casa das centenas, 4 na casa das dezenas e 3 na casa das unidades.
5 * 4 * 3 = 60 números
Observe que na situação envolvendo números distintos, as possibilidades de posicionamento da casa das centenas, dezenas e unidades foram diferentes. Essa condição anula a possibilidade de ocorrer números iguais, condicionando a multiplicação, a fornecer o resultado de forma exata.
Exemplo 2
Uma senha de 6 dígitos deve ser escolhida com a utilização dos algarismos representantes da base decimal: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9. A condição estabelecida informa que os números precisam ser distintos, assegurando senhas complexas. Quantas senhas podem ser formadas?
10 * 9 * 8 * 7 * 6 * 5 = 151.200
Podem ser formadas 151.200 senhas.
www.mundoeducacao.com.br
Esse é o blog do Professor de Matemática Carlos Barroso. Trabalho no Colégio Estadual Dinah Gonçalves . Valéria-Salvador-Bahia .Inscreva-se Já no meu canal www.youtube.com/accbarroso1 e receba as videoaulas de Matemática.
sexta-feira, 28 de fevereiro de 2020
Histologia animal

Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Tecidos animais.
Tecidos são agrupamentos de células e determinadas estruturas que, atuando de forma integrada, desempenham funções específicas. Assim, estão presentes somente em organismos multicelulares, tais como animais e plantas; o que não quer dizer que todos estes representantes os possuem. Este é o caso das algas e fungos multicelulares e esponjas.
Na Biologia, a ciência que estuda os tecidos é denominada Histologia (do grego: hydton = tecido + logos = estudos), sendo o principal enfoque desta os tecidos de animais vertebrados.
Proteção, absorção e secreção de substâncias, percepção de sensações, sustentação, locomoção, movimentação de órgãos internos, transmissão de informações, preenchimento, armazenamento, regeneração, defesa, transporte de sustâncias são algumas funções que os tecidos exercem.
Estes podem ser de quatro tipos:
- Tecidos epiteliais; que podem ser classificados em tecidos epiteliais de revestimento ou glandulares.
- Tecidos conjuntivos; divididos em tecido conjuntivo frouxo, denso, adiposo, reticular, cartilaginoso e ósseo.
- Tecidos musculares; do tipo estriado esquelético, estriado cardíaco ou liso.
- Tecido nervoso, cujos principais componentes são os neurônios e células da glia.
Tais tecidos associam-se e formam órgãos corporais. Assim, um único órgão geralmente possui mais de um tecido, estes especializados em aspectos distintos. A traqueia, por exemplo, é constituída de tecido muscular liso, reforçada com anéis cartilaginosos e revestida internamente por epitélio do tipo cilíndrico ciliado.
www.mundoeducacao.com.br
Sistema endócrino Regulação e controle das funções do corpo

Colégio Estadual Dinah Gonçalves
email
accbarroso@hotmail.com
Tireoide, glândula do sistema endócrino humano
O sistema endócrino, em conjunto com o sistema nervoso, regula e controla todas as funções de nosso organismo. Só para citar alguns poucos exemplos, o sistema endócrino atua no crescimento de tecidos, no equilíbrio hídrico do corpo, na reprodução e no metabolismo de carboidratos. Ele é formado por uma série de glândulas, chamadas de glândulas endócrinas.
As glândulas endócrinas secretam os hormônios, substâncias que são lançadas na corrente sanguínea, atingindo as células dos diversos tecidos do corpo humano. Os hormônios podem estimular ou inibir as funções metabólicas. Cada hormônio atua apenas sobre algumas células específicas, são as chamadas células-alvo. Alguns hormônios também atuam em conjunto ou em oposição a outros.
As principais glândulas endócrinas humanas são: a pineal, a hipófise, a tireoide, as paratireoides, as suprarrenais, o pâncreas, os ovários (nas mulheres) e os testículos (nos homens). Agora veremos um pouco sobre as funções e os hormônios secretados por cada uma delas.
Pineal
A pineal é uma pequena glândula situada no centro do cérebro. Sua principal função é o controle dos ciclos diários de sono e vigília. Durante a noite, a escuridão estimula a secreção de um hormônio da pineal, a melatonina, que induz ao sono. Já a claridade inibe a produção de melatonina.
Hipófise
A hipófise, ou pituitária, é uma pequena glândula, situada sob o encéfalo e ligada ao hipotálamo. Além de controlar diretamente diversas funções metabólicas, a hipófise também estimula ou inibe a ação de outras glândulas. Ela é dividida em duas regiões, uma posterior, chamada de neuro-hipófise, e outra anterior, a adeno-hipófise.
A neuro-hipófise secreta principalmente dois hormônios: a ocitocina e o hormônio antidiurético (ADH). A ocitocina atua sobre o útero, promovendo as contrações do parto, e sobre as glândulas mamárias, estimulando a secreção do leite. O ADH controla o equilíbrio hídrico do organismo. Ele atua sobre os rins aumentando a reabsorção de líquidos.
A adeno-hipófise secreta diversos hormônios. Alguns deles são: a somatotrofina (GH), o hormônio folículo estimulante (FSH), o hormônio luteinizante (LH), a prolactina e o hormônio tireotrófico (TSH).
A somatotrofina estimula a multiplicação celular e o desenvolvimento de tecidos. Consequentemente, o GH estimula o crescimento do corpo, sendo, por isso, conhecido também como "hormônio do crescimento".
Nas mulheres, o FSH atua sobre os ovários, promovendo o amadurecimento dos folículos e estimulando a liberação de estrogênio. Nos homens, o FSH atua sobre os testículos, estimulando a produção de testosterona.
O LH estimula a ovulação nas mulheres e a produção de testosterona nos homens. A prolactina atua sobre as glândulas mamárias, estimulando a produção de leite após o parto. O TSH atua sobre a tireoide, outra glândula do sistema endócrino, regulando a sua atividade.
Tireoide
A tireoide é uma glândula situada na região frontal do pescoço. Os principais hormônios secretados pela tireoide são: a tiroxina (T4), a triidoxina (T3) e a calcitonina. O T4 e o T3 regulam o metabolismo celular. Já a calcitonina regula a concentração de cálcio, elemento importante para a contração muscular.
Tanto a falta quanto o excesso de hormônios tireoidianos provocam doenças. O primeiro caso é conhecido como hipotiroidismo. Nesta disfunção, a baixa concentração de hormônios tireoidianos provoca uma redução do metabolismo, levando a consequências como ganho de peso, cansaço e disfunções intestinais.
Já no hipertiroidismo, o excesso de hormônios tireoidianos provoca um aumento do metabolismo, levando a sintomas como perda de peso, aumento de apetite, agitação e taquicardia.
Paratireóides
Ligadas à parte posterior da tireóide, existem quatro pequenas glândulas endócrinas, chamadas paratireoides. As paratireoides secretam o paratormônio (PTH), que atua na regulação da concentração de cálcio no organismo.
Suprarrenais
As glândulas suprarrenais, ou adrenais, estão localizadas sobre os rins. Internamente, são divididas em duas regiões, uma externa, o córtex adrenal, e outra interna, a medula adrenal.
Dois dos principais hormônios secretados pelo córtex adrenal são o cortisol e a aldesterona. Ambos são derivados do colesterol e, por isso, são chamados de esteroides. A principal função do cortisol é regular a permeabilidades dos capilares sanguíneos. Já a aldesterona atua sobre os rins, aumentado a absorção de sais durante o processo de filtração do sangue.
Os principais hormônios secretados pela medula adrenal são a adrenalina e a noradrenalina. A adrenalina prepara o organismo para situações de perigo ou estresse. Entre outros efeitos, ela aumenta os batimentos cardíacos e a pressão arterial, preparando o indivíduo para uma reação rápida. A noradrenalina controla a pressão sanguínea do corpo.
Pâncreas
O pâncreas é uma glândula mista localizada na região abdominal. Ele é chamado de glândula mista pelo fato de possuir tanto funções endócrinas quanto exócrinas. A função endócrina é realizada por diversos conjuntos de células chamadas de ilhotas de Langerhans.
Dois dos principais hormônios produzidos pelas ilhotas de Langerhans são a insulina e o glucagon, ambos relacionados ao controle da concentração de glicose no sangue. A insulina estimula a absorção da glicose presente no sangue e o seu armazenamento no fígado, na forma de glicogênio. Já o glucagon estimula o aumento da concentração de glicose no sangue e a quebra do glicogênio.
A deficiência de insulina provoca uma doença conhecida como diabete melito. A baixa concentração de insulina dificulta a absorção de glicose, afetando o metabolismo celular e, consequentemente, provocando um aumento dessa substância no sangue
Ovários
Os ovários secretam os hormônios sexuais femininos, o estrógeno e a progesterona. O estrógeno, entre outras funções, está relacionado ao ciclo menstrual e ao desenvolvimento de características sexuais secundárias femininas, como os seios e o acúmulo de gordura em certas regiões do corpo. A progesterona promove alterações necessárias para a manutenção de uma possível gravidez. No útero, por exemplo, o hormônio promove a formação do endométrio, tecido sobre o qual o embrião se fixa.
Testículos
Os testículos secretam o hormônio sexual masculino, a testosterona. Este hormônio, entre outras funções, promove o desenvolvimento de características sexuais secundárias masculinas, tais como voz grossa e barba.
Alice Dantas Brites é professora de biologia.
Marsupiais Mamíferos como o canguru, o gambá e o coala

Colégio Estadual Dinah Gonçalves
email
accbarroso@hotmail.com
O gambá possui hábitos noturnos, alimenta-se de frutos e pequenos animais
Animais como o canguru, o gambá, a cuíca, o diabo-da-tasmânia e o coala são chamados de marsupiais. O nome "marsupial" vem do latim marsupiu, que significa pequena bolsa, e está relacionado à presença de uma bolsa de pele, conhecida como marsúpio, que fica no ventre da fêmea.
Nem todos os marsupiais, porém, possuem um marsúpio bem desenvolvido. Em algumas espécies, essa bolsa só se forma durante o período reprodutivo. Em outras, está totalmente ausente.
Acredita-se que os marsupiais tenham se originado na América do Norte, durante o Cretáceo Inferior, e de lá se dispersado para a América do Sul, Europa, Ásia, norte da África e Oceania. No entanto, durante o Cenozóico Médio, sofreram uma grande extinção e, atualmente, o único marsupial encontrado na América do Norte é uma espécie de gambá (Didelphis sp.). Hoje em dia a maioria das espécies é encontrada na América do Sul e na Austrália.
Alguns cientistas acreditam que este desaparecimento ocorreu devido à competição com os mamíferos eutérios, outros afirmam que foi apenas uma conseqüência da extinção de muitos mamíferos que ocorreu naquela era.
Reprodução diferente
O aparelho reprodutor dos marsupiais é bem diferente dos demais mamíferos. As fêmeas possuem dois úteros, duas vaginas laterais e uma vagina mediana, também chamada de canal pseudovaginal.
As vaginas laterais servem apenas para conduzir o esperma para o interior dos úteros. O canal pseudovaginal permanece fechado até o momento do parto, quando se abre para permitir o nascimento do filhote.
Já os machos possuem um pênis bifurcado que possibilita a disseminação do sêmen para o interior das duas vaginas da fêmea. Os marsupiais possuem apenas a placenta cório-vitelínica, desenvolvida a partir de membranas embrionárias.
Gestação e nascimento
O período de gestação costuma ser muito breve, em geral por volta de 40 dias. Os marsupiais recém-nascidos são chamados de altriciais. Este nome é atribuído a todos os filhotes que nascem num estágio pouco desenvolvido e, por isso, dependem de um cuidado parental intensivo.
Os frágeis marsupiais nascem com cerca de 2 a 5 cm de comprimento, ainda não enxergam nem possuem pêlos. No entanto, os seus membros anteriores são bem desenvolvidos assim como os músculos faciais e da língua. Estas características permitem que eles se prendam fortemente aos mamilos existentes no interior do marsúpio e comecem a mamar imediatamente.
Os filhotes permanecem no marsúpio até completar seu desenvolvimento. Nas espécies que não possuem marsúpio, os filhotes ficam agarrados aos mamilos das mães entre pequenas dobras de pele da região ventral.
O tempo de desenvolvimento dos filhotes no interior do marsúpio é bem maior do que o período de gestação, levando de algumas semanas até meses. E, em vários grupos, a lactação continua mesmo nos indivíduos jovens, que podem ser observados entrando e saindo da bolsa da fêmea.
Geralmente, como é o caso dos cangurus, para chegar até o marsúpio os filhotes literalmente escalam o corpo da mãe, agarrando-se em seus pêlos. Esta apenas lambe o caminho entre a vagina e a bolsa, mas não o ajuda em sua escalada. Existem algumas espécies nas quais os filhotes, ao nascerem, caem diretamente da vagina para o interior do marsúpio.
Hábitos
Os marsupiais possuem diversos hábitos alimentares e de locomoção. Existem espécies carnívoras, como o diabo-da-tasmânia, herbívoras, como os coalas, e onívoras, como os gambás. Algumas espécies estão adaptadas para viver sobre as árvores (arborícolas), outras para cavar túneis subterrâneos, enquanto outras podem correr atingindo grandes velocidades.
O canguru, por exemplo, possui os membros posteriores alongados e musculosos sendo capaz de correr a uma velocidade de cerca de 50 km por hora e saltar até 2 m de altura.
Marsupiais no Brasil
Dois marsupiais muito comuns no Brasil são o gambá e a cuíca. O gambá possui hábitos noturnos, alimenta-se de frutos e pequenos animais. Muito comum na mata atlântica, ele se adapta facilmente às áreas urbanas e pode ser visto em ruas ou sobre árvores. Como forma de defesa, sempre que se sente ameaçado, o gambá pode se fingir de morto e exalar um forte odor. É inofensivo ao homem, porém, por falta de informação, muitas vezes é confundido com ratazanas ou é tido como uma espécie ameaçadora, sendo morto de forma cruel.
A cuíca também possui hábitos noturnos e alimenta-se de pequenos frutos. É considerada uma espécie muito importante para a dispersão das sementes de algumas árvores. Isso porque a cuíca é capaz de percorrer grandes distâncias no interior das matas à procura de alimento. Nesta busca, as cuícas acabam espalhando, junto com as suas fezes, as sementes dos frutos que ingeriram. Diferentemente dos gambás, as cuícas não são comuns em ambientes urbanos.
Classificação
Os marsupiais são mamíferos pertencentes à subclasse Theria. Esta subclasse é dividida em duas infraclasses: Metatheria e Eutheria.
Os metatérios são os marsupiais e os eutérios correspondem aos mamíferos chamados de placentários. Existem cerca de 260 espécies de marsupiais, sendo que a grande maioria é nativa da Austrália ou das ilhas vizinhas. A menor espécie de marsupial mede apenas alguns centímetros e não chega a pesar nem 10 gramas.
*Alice Dantas Brites é professora de biologia.
Volume do tronco de pirâmide

Pirâmide
Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
www.accbarrosogestar.wordpress.com
Quando um plano intercepta uma pirâmide a uma determinada altura, paralelamente à sua base, obtém-se uma nova forma geométrica, denominada tronco de pirâmide. O tronco de pirâmide apresenta duas bases (base maior e base menor) e sua superfície lateral é composta de trapézios.
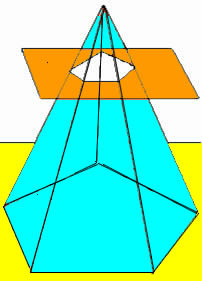
O volume do tronco de pirâmide é obtido fazendo a diferença entre o volume da pirâmide original e o volume da pequena pirâmide formada após a intersecção do plano. Dessa maneira, obtemos a fórmula que determina o volume do tronco de qualquer pirâmide.
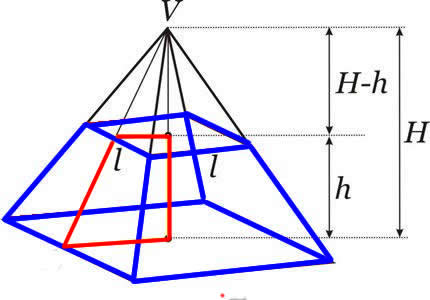
Fórmula do volume do tronco de pirâmide:
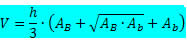
Onde
h → é a altura do tronco de pirâmide.
AB → é a área da base maior.
Ab → é a área da base menor.
Observe os seguintes exemplos para compreender como utilizar a fórmula.
Exemplo 1. Calcule o volume do tronco de pirâmide abaixo.
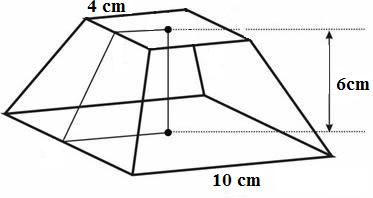
Solução: Observe que as bases desse tronco de pirâmide são quadrados e sua altura é de 6 cm. Para calcular o volume de um tronco de pirâmide qualquer, precisamos da área das duas bases e da medida da altura. Assim, teremos:
AB = 102 = 100 cm2
Ab = 42 = 16 cm2
h=6cm
Substituindo esses valores na fórmula do volume, obtemos:
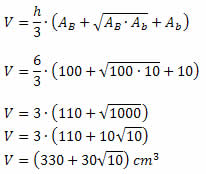
Exemplo 2. A base maior de um tronco de pirâmide é uma das faces de um cubo de 125 cm3 de volume. Sabendo que a base menor desse tronco é um quadrado de 2 cm de lado e sua altura é de 9 cm, calcule seu volume.
Solução: Como a base maior do tronco é uma das faces de um cubo, sabemos que sua base é um quadrado. Foi dado que o volume desse cubo é de 125 cm3, assim, cada aresta do cubo mede 5 cm. Dessa forma, a base maior do tronco é um quadrado de 5 cm de lado. Logo, teremos:
AB = 52 = 25 cm2
Ab = 22 = 4 cm2
h = 9 cm
Substituindo na fórmula do volume, teremos:
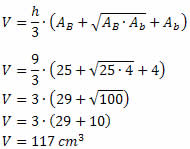
Marcelo Rigonatto
Sistema Reprodutor
O sistema reprodutor é um termo aplicado a um grupo de órgãos necessários ou acessórios aos processos de reprodução. As unidades básicas da reprodução sexual são as células germinais masculinas e femininas.
Ciclo de resposta sexual, dividido em quatro fases:
1º) Excitação
Inicio da resposta sexual, o pênis e o clitóris sofrem ereção. Na mulher, os lábios vulvares intumescem, os mamilos se eriçam, a vagina se alonga e passa a produzir uma secreção lubrificante.
2º) Fase de Estabilização
A circulação sanguínea nos órgãos genitais e a tensão muscular aumentam. A porção interna da vagina expande-se e o útero eleva-se, se preparando para receber o esperma. Os movimentos respiratórios aumentam e o batimento cardíaco acelera. A cópula ou coito, que é a introdução do pênis na vagina, leva ao orgasmo.
3º) Fase de Orgasmo
É o clímax da excitação sexual e se caracteriza pelas contrações rítmicas e involuntárias dos órgãos do sistema reprodutor de ambos os sexos. No homem, durante o orgasmo, as contrações das glândulas acessórias e os dutos espermáticos trazem o esperma até a uretra, ocorrendo a ejaculação em seguida. No orgasmo feminino, o útero e a porção mais externa da vagina também se contraem.
4º) Fase de Dissolução
A musculatura se relaxa, os órgãos começam a voltar ao normal. A maioria dos homens apresenta após o orgasmo, um período refratório onde não ocorre resposta ao estímulo sexual. A duração desse período varia em diferentes indivíduos e situações. Já a maioria das mulheres, pode repetir o ciclo sexual imediatamente se for estimulada.
Fecundação
Os espermatozóides depositados no fundo da vagina no ato sexual, nadam para o interior do útero, de onde atingem os ovidutos. Durante a viagem à trompa, muitos espermatozóides morrem, devido as condições desfavoráveis de acidez ou são devorados por macrófagos, células responsáveis pela limpeza do sistema reprodutor feminino. Mesmo assim, milhares de espermatozóides atingem o óvulo. O primeiro espermatozóide a tocar na membrana do óvulo, penetra, fenômeno denominado fecundação ou fertilização. O óvulo estimulado pela entrada do gameta masculino, completa a meiose e elimina o segundo corpúsculo polar. Finalmente o pronúcleo masculino se funde ao núcleo do óvulo, originando o núcleo do zigoto.

Embrião
O desenvolvimento embrionário tem início ainda na trompa, logo após a fertilização. Cerca de 24h após a penetração do espermatozóide, o zigoto se divide, formando as duas primeiras células embrionárias, que se dividem novamente, produzindo quatro células, que se dividem produzindo oito e assim sucessivamente. As divisões celulares continuam ocorrendo à medida que o embrião se desloca pela trompa em direção ao útero, depois de 3 dias após a fecundação.
Após permanecer livre na cavidade uterina por cerca de 3 a 4 dias, nutrindo-se de substâncias produzidas por glândulas do endométrio, o embrião então, implanta-se na mucosa uterina, processo chamado de nidação.
www.colaweb.com
Ciclo de resposta sexual, dividido em quatro fases:
1º) Excitação
Inicio da resposta sexual, o pênis e o clitóris sofrem ereção. Na mulher, os lábios vulvares intumescem, os mamilos se eriçam, a vagina se alonga e passa a produzir uma secreção lubrificante.
2º) Fase de Estabilização
A circulação sanguínea nos órgãos genitais e a tensão muscular aumentam. A porção interna da vagina expande-se e o útero eleva-se, se preparando para receber o esperma. Os movimentos respiratórios aumentam e o batimento cardíaco acelera. A cópula ou coito, que é a introdução do pênis na vagina, leva ao orgasmo.
3º) Fase de Orgasmo
É o clímax da excitação sexual e se caracteriza pelas contrações rítmicas e involuntárias dos órgãos do sistema reprodutor de ambos os sexos. No homem, durante o orgasmo, as contrações das glândulas acessórias e os dutos espermáticos trazem o esperma até a uretra, ocorrendo a ejaculação em seguida. No orgasmo feminino, o útero e a porção mais externa da vagina também se contraem.
4º) Fase de Dissolução
A musculatura se relaxa, os órgãos começam a voltar ao normal. A maioria dos homens apresenta após o orgasmo, um período refratório onde não ocorre resposta ao estímulo sexual. A duração desse período varia em diferentes indivíduos e situações. Já a maioria das mulheres, pode repetir o ciclo sexual imediatamente se for estimulada.
Fecundação
Os espermatozóides depositados no fundo da vagina no ato sexual, nadam para o interior do útero, de onde atingem os ovidutos. Durante a viagem à trompa, muitos espermatozóides morrem, devido as condições desfavoráveis de acidez ou são devorados por macrófagos, células responsáveis pela limpeza do sistema reprodutor feminino. Mesmo assim, milhares de espermatozóides atingem o óvulo. O primeiro espermatozóide a tocar na membrana do óvulo, penetra, fenômeno denominado fecundação ou fertilização. O óvulo estimulado pela entrada do gameta masculino, completa a meiose e elimina o segundo corpúsculo polar. Finalmente o pronúcleo masculino se funde ao núcleo do óvulo, originando o núcleo do zigoto.

Embrião
O desenvolvimento embrionário tem início ainda na trompa, logo após a fertilização. Cerca de 24h após a penetração do espermatozóide, o zigoto se divide, formando as duas primeiras células embrionárias, que se dividem novamente, produzindo quatro células, que se dividem produzindo oito e assim sucessivamente. As divisões celulares continuam ocorrendo à medida que o embrião se desloca pela trompa em direção ao útero, depois de 3 dias após a fecundação.
Após permanecer livre na cavidade uterina por cerca de 3 a 4 dias, nutrindo-se de substâncias produzidas por glândulas do endométrio, o embrião então, implanta-se na mucosa uterina, processo chamado de nidação.
www.colaweb.com
Adição com números Naturais
Colégio Estadual Dinah Gonçalves
email
accbarroso@hotmail.com
A primeira operação fundamental da Aritmética tem por finalidade reunir em um só número, todas as unidades de dois ou mais números. Antes de surgir os algarismos indo-arábicos, as adições podiam ser realizadas por meio de tábuas de calcular, com o auxílio de pedras ou por meio de ábacos.
Propriedades da Adição com números naturais
Fechamento: A adição no conjunto dos números naturais é fechada, pois a soma de dois números naturais é ainda um número natural. O fato que a operação de adição é fechada em N é conhecido na literatura do assunto como: A adição é uma lei de composição interna no conjunto N.
Por exemplo:
Resolva estas adições:
15 + 17 =
27 + 15 =
8 + 13 =
35 + 87 =
45 + 50 =
63 + 84 =
Associativa: A adição no conjunto dos números naturais é associativa, pois na adição de três ou mais parcelas de números naturais quaisquer é possível associar as parcelas de quaisquer modos, ou seja, com três números naturais, somando o primeiro com o segundo e ao resultado obtido somarmos um terceiro, obteremos um resultado que é igual à soma do primeiro com a soma do segundo e o terceiro.
Alice tem 8 pares de meia rosa, 12 pares de meia azul e 15 pares de meia amarela. Quantos pares de meia têm Alice?
Vejamos como podemos resolver este exercício:
Elemento neutro: No conjunto dos números naturais, existe o elemento neutro que é o zero, pois tomando um número natural qualquer e somando com o elemento neutro (zero), o resultado será o próprio número natural.
Por exemplo:
Em um jogo de Basquete, um time fez 27 pontos no primeiro tempo. No segundo tempo o time não fez nenhum ponto. Quantos pontos o time de basquete fez ao todo no jogo?
27 + 0 = 27
O time de basquete fez 27 pontos ao todo.
Resolva este problema:
Elisa estava recolhendo flores, no jardim da sua avó para levar par sua tia á noite, pela manhã recolheu 14 rosas. Á tarde, Elisa não conseguiu recolher nenhuma, pois chovia muito. Então quantas flores Elisa levou para sua tia?
Elisa levou flores para sua tia.
Comutativa: No conjunto dos números naturais, a adição é comutativa, pois a ordem das parcelas não altera a soma, ou seja, somando a primeira parcela com a segunda parcela, teremos o mesmo resultado que se somando a segunda parcela com a primeira parcela.
Por exemplo:
Resolva estas duas continhas:
26 + 31 =
31 + 26 =
Repare que a ordem das parcelas é diferente, mas o resultado das duas contas é o mesmo.
www.colegioweb.com.br
Equação do Segundo Grau
Denomina-se equação do 2° grau, qualquer sentença matemática que possa ser reduzida à forma ax2 + bx + c = 0, onde x é a incógnita e a, b e c são números reais, com a ≠ 0. a, b e c são coeficientes da equação. Observe que o maior índice da incógnita na equação é igual a dois e é isto que a define como sendo uma equação do segundo grau.
Equação do 2° grau completa e equação do 2° grau incompleta
Da definição acima temos obrigatoriamente que a ≠ 0, no entanto podemos ter b = 0 e/ou c = 0.Caso b ≠ 0 e c ≠ 0, temos uma equação do 2° grau completa. A sentença matemática -2x2 + 3x - 5 = 0 é um exemplo de equação do 2° grau completa, pois temos b = 3 e c = -5, que são diferentes de zero.
-x2 + 7 = 0 é um exemplo de equação do 2° grau incompleta, pois b = 0.
Neste outro exemplo, 3x2 - 4x = 0 a equação é incompleta, pois c = 0.
Veja este último exemplo de equação do 2° grau incompleta, 8x2 = 0, onde tanto b, quanto c são iguais a zero.
Resolução de equações do 2° grau
A resolução de uma equação do segundo grau consiste em obtermos os possíveis valores reais para a incógnita, que torne a sentença matemática uma equação verdadeira. Tais valores são a raiz da equação.Fórmula Geral de Resolução
Para a resolução de uma equação do segundo grau completa ou incompleta, podemos recorrer à fórmula geral de resolução:Esta fórmula também é conhecida como fórmula de Bhaskara.
O valor b2 -4ac é conhecido como discriminante da equação e é representado pela letra grega Δ. Temos então que Δ = b2 -4ac, o que nos permitir escrever a fórmula geral de resolução como:
Resolução de equações do 2° grau incompletas
Para a resolução de equações incompletas podemos recorrer a certos artifícios. Vejamos:
Para o caso de apenas b = 0 temos:
Portanto para equações do tipo ax2 + c = 0, onde b = 0, podemos utilizar a fórmula simplificada
Para o caso de apenas c = 0 temos:
Portanto para equações do tipo ax2 + bx = 0, onde c = 0, uma das raízes sempre será igual a zero e a outra será dada pela fórmula
Para o caso de b = 0 e c = 0 temos:
Podemos notar que ao contrário dos dois casos anteriores, neste caso temos apenas uma única raiz real, que será sempre igual a zero.
Discriminante da equação do 2° grau
O cálculo do valor do discriminante é muito importante, pois através deste valor podemos determinar o número de raízes de uma equação do segundo grau.Como visto acima, o discriminante é representado pela letra grega Δ e equivale à expressão b2 - 4ac, isto é: Δ = b2 - 4ac.
Discriminante menor que zero
Caso Δ <>, a equação não tem raízes reais, poisDiscriminante igual a zero
Caso Δ = 0, a equação tem duas raízes reais e iguais, pois
Discriminante maior que zero
Caso Δ > 0, a equação tem duas raízes reais e diferentes, pois
Conjunto Verdade de equações do 2° grau
A partir do estudado acima, podemos esquematizar o conjunto verdade das equações do segundo grau completas e incompletas como a seguir:
Para o caso das equações completas temos:
Para o caso das equações incompletas onde somente b = 0 temos:
Para o caso das equações incompletas onde somente c = 0 temos:
E no caso das equações incompletas onde tanto b = 0, quanto c = 0 temos:
Exemplo de resolução de uma equação do segundo grau
 Encontre as raízes da equação: 2x2 - 6x - 56 = 0
Encontre as raízes da equação: 2x2 - 6x - 56 = 0Aplicando a fórmula geral de resolução à equação temos:
Observe que temos duas raízes reais distintas, o que já era de se esperar, pois apuramos para Δ o valor 484, que é maior que zero.
Logo:
 As raízes da equação 2x2 - 6x - 56 = 0 são: -4 e 7.
As raízes da equação 2x2 - 6x - 56 = 0 são: -4 e 7.Anelídeos

Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Representantes dos anelídeos portadores de cerdas.
Filo do Reino Animal constituído por animais invertebrados triblásticos, celomados, de corpo cilíndrico, possuindo simetria bilateral e metamerização interna e externa do corpo, formado por vários anéis. Seus representantes, com ampla distribuição, habitam ambientes aquáticos ou terrestres.
As principais características anatômicas internas desses organismos são:
- Sistema Digestório: constituído por boca, faringe, papo, moela, intestino e ânus;
- Sistema Circulatório: fechado e com vasos contráteis (corações), que atuam impulsionando o sangue;
- Sistema Excretor: formado por metanefrídeos;
- Sistema Respiratório: realizado por difusão entre as camadas da epiderme (cutânea), ou branquiais, através de codificações do aparelho locomotor de algumas espécies;
- Sistema Nervoso: ganglionar, composto de diversos gânglios ligados entre si por cordões nervosos ventrais.
- Sistema Reprodutor: nos organismos dióicos, ocorre por processos sexuados; e nos monóicos, por fecundação cruzada.
A classificação do Filo Annelida (seres segmentados)
Classe Oligochaeta (oligo = pouco; chaeta = cerdas) → são anelídeos com poucas cerdas no corpo, possuindo uma região epidérmica espaçada, o clitelo, sendo responsável pela síntese de um casulo que abrigará os ovos fecundados durante a reprodução.
Exemplo: as minhocas.
Classe Polychaeta (poly = várias; chaeta = cerdas) → são anelídeos portadores de inúmeras cerdas inseridas em projeções laterais ao corpo, formando estruturas denominadas parapódios que auxiliam na locomoção. Esses animais são desprovidos de clitelo. A maioria das espécies deste grupo se reproduz sexuadamente, possuindo fertilização externa que resulta na formação de larvas livre nadantes.
Exemplo: Nereis (organismo marinho).
Classe Hirudínea → anelídeos sem cerdas e com ventosas bucais e na região posterior do corpo. São hermafroditas, com fecundação cruzada e desenvolvimento direto.
Exemplo: sanguessuga.
www.mundoeducacao.com.br
Sistema Nervoso
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Sistema Nervoso
Na nossa relação com o mundo, o tempo inteiro somos estimulados e respondemos aos elementos do ambiente. A cada estímulo externo (como o cheiro de um alimento ou o som de uma buzina) e mesmo interno (como dor ou sensação de fome), o organismo reage, ou seja, de certo modo “responde a essas perguntas:
De onde vem o estímulo?
Como meu corpo reage a esse estímulo?
Isto me fará bem ou mal?
Já tive essa sensação antes?
Esse processo ocorre no sistema nervoso central de maneira tão instantânea que a nossa consciência não tem como identificar todas as suas etapas, nem os milhares de estímulos que o corpo recebe a todo instante.
Para compreender melhor como percebemos os estímulos externos e como respondemos a eles, é fundamental reconhecer o sistema que forma a rede de comunicação do corpo.
Por que precisamos de um sistema nervoso?
Seu cérebro é o órgão mais importante de seu corpo. Ele controla tudo o que você faz, seus movimentos, seus pensamentos e sua memória. Muitas vezes ele não age diretamente, mas pode controlar pequenas quantidades de substâncias químicas do sangue, que, por sua vez, têm um forte efeito sobre outra parte do corpo.

Embora pareça muito simples, o cérebro é imensamente complicado. E uma massa de tecido esbranquiçado, bastante mole ao tato, que ocupa cerca de metade do volume da cabeça. Fica posicionado no alto da cabeça, acima dos olhos e dos ouvidos, estendendo para trás e para a parte inferior da cabeça.
Quase tão importante quanto o cérebro é o restante do sistema nervoso. A medula espinhal estende-se do cérebro para baixo, ao longo da coluna, O cérebro e a medula espinhal formam o sistema nervoso central.
Ao longo do comprimento da medula espinhal saem nervos semelhantes a fios que se dividem e se ligam com quase todas as partes do corpo. Os nervos transportam mensagens dos órgãos dos sentidos para o cérebro, e também instruções do cérebro para outras partes do corpo. O cérebro funciona como uma rede telefônica complicada, mas muito compacta, com um complexo fluxo de mensagens que chegam, são selecionadas e depois dirigidas a seu destino apropriado.
As membranas protetoras do cérebro
Por ser um órgão tão importante, o cérebro precisa de boa proteção contra acidentes. Ficando em pé, o ser humano mantém o cérebro e a cabeça afastados de choques e batidas. Mesmo assim, é necessária uma proteção muito confiável. Por isso o cérebro fica alojado no crânio, uma dura caixa óssea.
Embora de paredes finas, o crânio é muito resistente devido a sua forma arredondada. Uma das formas mais fortes que se conhece é uma bola rígida. Um ovo, por exemplo, é extremamente resistente, considerando-se como é fina sua casca. Assim, o mole e delicado cérebro é protegido contra danos externos diretos pelo resistente crânio. Entretanto, mesmo sendo o crânio rígido e forte, um abalo violento poderia balançar o cérebro e causar-lhe danos. É preciso, então, maior proteção, que é dada por três membranas, denominadas meninges, que recobrem completamente o cérebro. A membrana mais externa é chamada de dura-máter, que fornece uma boa proteção e apoio devidos a sua constituição forte e coriácea.

Junto ao cérebro há uma outra membrana, denominada pia-máter, muito mais fina, que acompanha cada depressão e cada elevação da superfície do cérebro. Entre essas duas membranas há uma terceira, de constituição esponjosa, a aracnóide. Os espaços desta membrana são preenchidos por um liquido no qual flutua todo o cérebro, fornecendo a camada protetora final. Há ainda grandes espaços dentro do cérebro, que também são preenchidos com o mesmo liquido da aracnóide, de modo que o delicado tecido do cérebro não se deforma quando movemos nossa cabeça.
A medula espinhal
A medula espinhal é uma extensão do cérebro, estendendo-se da base do crânio até logo abaixo das costelas. E uma haste de tecido cerebral, com um pequeno canal passando através de todo seu comprimento. Toda a medula é coberta por membranas, tal como o cérebro, e é também banhada por dentro e por fora com o mesmo líquido protetor do cérebro.
Como o cérebro, a medula espinhal precisa de proteção. Enquanto o cérebro está seguramente encerrado em um crânio rígido, a medula espinhal está cercada por um conjunto de ossos chamados vértebras. Estes formam a coluna vertebral, que é capaz de flexionar-se quando nos dobramos ou movemos. Ao mesmo tempo, a coluna vertebral tem que ser forte o suficiente para suportar o peso do corpo e dar proteção segura à coluna espinhal. Poderia parecer que flexibilidade, força e proteção de seu frágil conteúdo não poderiam ser obtidos pela coluna vertebral, mas sua construção engenhosa toma tudo isso possível.

A coluna vertebral é constituída por mais de duas dúzias de vértebras em forma de anel. A medula espinhal passa através do buraco existente no centro de cada uma das vértebras, e é completamente protegida pelos arcos ósseos. As protuberâncias ósseas das vértebras articulam-se de maneira que cada vértebra pode mover-se apenas um pouco, para não apertar ou machucar a medula espinhal. Entre cada par de vértebras há pequenas aberturas através das quais os nervos podem passar, ramificando-se a partir da própria medula espinhal. A complicada estrutura da coluna é mantida unida por flexíveis cordões de ligamento e por músculos poderosos.
A estrutura do encéfalo
O encéfalo se parece com uma noz grande, de cor rosa clara. Sua superfície é profundamente enrugada e cheia de dobras, e sua parte superior está quase dividida em duas partes por um sulco muito profundo. Essa superfície enrugada ocupa a maior parte do encéfalo e é chamada de cérebro. Na maioria dos animais o cérebro é bem pequeno, mas no homem ele cresceu tanto que cobre todo o resto do encéfalo.

O cérebro, junto com outras partes do encéfalo, cresce do tronco cerebral, que é uma expansão no topo da medula espinhal. Um pouco mais abaixo do tronco cerebral está o cerebelo, com apenas 1/8 do tamanho do cérebro, mas bastante semelhante em sua aparência exterior. E até mesmo mais enrugado, e está colocado diretamente na parte de trás da cabeça. O tálamo e o hipotálamo, outras partes menores do encéfalo, também crescem do tronco cerebral, sendo completamente cobertos pela massa do cérebro. Uma série de grandes espaços, ou ventrículos, atravessam toda a estrutura do cérebro, e são preenchidos com líquido.
O tronco cerebral
O tronco cerebral, onde se localiza o bulbo, é algumas vezes chamado de a parte mais velha do cérebro, porque é a principal parte do cérebro na maioria dos animais primitivos. Controla a maior parte das funções importantes do corpo, e é o sistema de sustentação da vida. Se o tronco cerebral não for prejudicado, é realmente possível o corpo permanecer vivo por algum tempo, mesmo depois que o resto do cérebro tenha sido destruído.
O tronco cerebral atua junto com a medula espinhal para controlar as funções vitais, como o batimento regular do coração, a pressão sanguínea e a respiração. Mas a função mais importante do tronco cerebral é controlar a consciência, desligando as atividades do cérebro quando dormimos e ligando quando acordamos. Mesmo quando dormimos o tronco cerebral controla e confere nossas atividades vitais, mantendo o corpo funcionando.

O tronco cerebral trabalha como um computador, continuamente conferindo e controlando as informações que entram no cérebro através do sistema nervoso; em seguida ele age em cima dessa informação liberando as mensagens para que o sistema nervoso controle o corpo inteiro. Não tomamos consciência de todas essas atividades; podemos apenas notar seus efeitos. O tronco cerebral controla funções, como a respiração, automaticamente.
Cerebelo
Se localiza abaixo do cérebro. Coordena, com o cérebro, os movimentos do corpo. É responsável pelo equilíbrio do corpo, pois está ligado a alguns canais da orelha interna. Além disso, mantém o tônus muscular, isto é, regula o grau de contração muscular dos músculos em repouso.
Como as mensagens passam pelos neurônios
Um sinal carregado por um neurônio pode parecer com uma corrente elétrica sendo carregada através de um fio, mas na realidade é bem diferente. Uma minúscula carga elétrica é produzida, mas o movimento do sinal ao longo de um axônio é mais semelhante à queima de um estopim de pólvora. O sinal move-se com uma velocidade entre 1,5 metros e 90 metros por segundo.
O axônio é um tubo fino cheio de substâncias químicas dissolvidas em água. Muitos têm a parte exterior coberta com uma camada de material gorduroso, como um isolamento elétrico. A passagem de um sinal ao longo do axônio envolve o movimento de íons, ou minúsculas partículas eletricamente carregadas de dois elementos metálicos: sódio e potássio. Normalmente há mais potássio do lado de dentro de um axônio e mais sódio do lado de fora. Quando passa um sinal, a membrana que cobre o axônio se altera, permitindo aos íons escoarem através dela, causando uma mudança súbita nas propriedades elétricas nesse ponto. Essas mudanças oscilam ao longo do axônio como uma onda.

Quando o sinal alcança a sinapse, ele deve cruzar um pequeno intervalo para alcançar o próximo neurônio. Minúsculas bolhas nas ramificações da extremidade dos axônios contêm substâncias químicas, chamadas transmissores. Estas são liberadas quando atingidas pelos sinais e então atravessam o intervalo da sinapse. Quando contatam os dendritos da célula seguinte, dão início ao movimento do sódio e do potássio, transmitindo o sinal.
Agora o primeiro neurônio volta ao estado de descanso normal, esperando por outro sinal. Os transmissores químicos que carregam um sinal através do intervalo da sinapse podem ser de dois tipos diferentes. Alguns são chamados de substâncias químicas excitadoras. Estas são as substâncias que passam a mensagem para o próximo neurônio, que em seguida, começa as mudanças elétricas que darão origem a sinais a serem produzidos e passados ao longo do axônio. Os outros transmissores são chamados de substâncias químicas inibidoras. Sua função é evitar que um sinal seja produzido em outro neurônio.
Milhares de neurônios estão em contato com os outros através de sinapse, e muitos estarão produzindo sinais excitadores ou inibidores, O neurônio não produzirá nenhum sinal a menos que receba mais mensagens excitadoras ("liga") do que inibidoras ("desliga").Um sinal de um ou dois neurônios não é suficiente para acionar um outro - ele deve receber vários sinais de uma vez. Isto significa que quaisquer sinais ocasionais de milhares de neurônios ao redor não causarão uma mensagem falsa a ser passada. E quase como o princípio da votação, onde o neurônio precisa dos "votos" de uma série de outros neurônios antes de ser capaz de emitir um sinal.
Rotas através do sistema nervoso
A atividade elétrica dos neurônios não tem lugar apenas no cérebro. Os nervos espalham-se pelo corpo todo desde o alto da cabeça até a ponta dos dedos dos pés. São feixes de axônios, ou fibras nervosas, dividindo-se e tomando-se mais finos quanto mais afastados estão do cérebro ou da medula espinhal. Os corpos das células dos neurônios estão agrupados na massa cinzenta, na superfície do cérebro, na massa cinzenta similar, na parte interna da medula espinhal, e em pequenos nódulos chamados gânglios, perto da coluna vertebral.
As mensagens dos órgãos dos sentidos, situados nos olhos, nariz, ouvidos e boca, dos órgãos do tato, espalhados por toda a superfície do corpo, e até mesmo em alguns órgãos internos, chegam ao cérebro através do sistema nervoso. Os neurônios que carregam essas mensagens para o cérebro são chamados neurônios sensoriais. Outros sinais passam do cérebro e da medula espinhal de volta para todo o corpo, sendo carregados pelos chamados neurônios motores.

Os sinais passam ao longo de todo o sistema muito rapidamente, mas não tão depressa quanto em um circuito elétrico normal. Leva um certo tempo para os sinais serem carregados através da sinapse pelas substâncias químicas transmissoras. Por esta razão os axônios dos nervos são imensamente compridos de maneira que a mensagem possa ser levada tão rápido quanto possível, sem ser retardada por sinapses desnecessárias.
A rede neurônica
É difícil perceber como podem ser complicadas as conexões das células nervosas. Os terminais das ramificações de um axônio não apenas tocam a célula mais próxima mas podem também estar em contato com outras 50.000 células ou mais. Sabemos que as mensagens passam de um neurônio para o seguinte na rede de células e que sinais repetidos geralmente passam pelo mesmo caminho. Se queremos dizer a palavra "cérebro", as instruções para a fala vêm do cérebro e passam ao longo de uma série de caminhos especiais. Se queremos dizer "cérebro" em voz mais baixa ou mais alta os músculos da caixa da voz (laringe) devem ser instruídos para se moverem de maneiras diferentes; então, as mensagens devem passar por caminhos diferentes.
O cérebro pode selecionar diferentes conjuntos de caminhos para obter resultados semelhantes. Por causa dessa habilidade, as pessoas podem, muitas vezes, sobrepujar danos cerebrais, aprendendo a usar partes diferentes do cérebro para duplicar as funções das partes prejudicadas. Isso é importante para nós, porque, ao contrário de outras células do corpo, as células do cérebro não podem crescer ou regenerar-se depois do nosso nascimento. Células cerebrais estão morrendo a cada minuto, mas temos as remanescentes tomando o seu lugar e geralmente não notamos qualquer efeito prejudicial.
Os reflexos
O controle cerebral é essencial para muitas de nossas funções, mas em algumas situações é necessário que o corpo reaja muito rapidamente, na verdade, sem esperar instruções. Essas reações de emergência são chamadas reflexos. Afastar o dedo de uma picada de alfinete é uma reação muito comum para evitar ferimentos. Isso acontece rapidamente, antes mesmo que possamos perceber o que houve. É um reflexo.

Mini órgãos sensoriais da pele chamados receptores, registram a picada do alfinete e imediatamente passam os sinais para os nervos que correm pelo braço em direção à medula espinhal. Os sinais são então transmitidos para outras fibras nervosas (neurônios) que os carregam para a massa cinzenta dentro da medula espinhal. Na medula, os sinais saem em duas direções. Alguns contatam fibras nervosas que os conduzem diretamente de volta aos músculos do braço. Eles fazem os músculos do braço reagirem violentamente, afastando a mão para longe da picada do alfinete. Enquanto isso, os outros sinais originais ainda estão sendo levados ao cérebro, através da medula espinhal.
Uma fração de segundo mais tarde percebemos que fomos picados. E dói. O cérebro instrui agora a cabeça e os olhos para se moverem e observarem o ferimento. Algumas vezes temos que levar uma picada quando recebemos uma vacina, por exemplo. Contudo, sabemos disso com antecedência, e, embora a picada da agulha acione um reflexo, o cérebro manda uma mensagem inibidora pela medula espinhal. Então o reflexo é contido antes de ser completado e o braço, portanto, não se afasta da picada.
O sistema nervoso periférico
O Sistema Nervoso Periférico é constituído pelos nervos e gânglios nervosos e sua função é conectar o sistema nervoso central às diversas partes do corpo humano.
Nervos e gânglios nervosos
Nervos são feixes de fibras nervosas envoltas por uma capa de tecido conjuntivo. Nos nervos há vasos sanguíneos, responsáveis pela nutrição das fibras nervosas. As fibras presentes nos nervos podem ser tanto dendritos como axônios que conduzem, respectivamente, impulsos nervosos das diversas regiões do corpo ao sistema nervoso central e vice-versa. Gânglios nervosos são aglomerados de corpos celulares de neurônios localizados fora do sistema nervoso central. Os gânglios aparecem como pequenas dilatações em certos nervos.
Nervos sensitivos, motores e mistos
Nervos sensitivos são os que contêm somente fibras sensitivas, que conduzem impulsos dos órgãos sensitivos para o sistema nervoso central. Nervos motores são os que contêm somente fibras motoras, que conduzem impulsos do sistema nervoso central até os órgãos efetuadores (músculos ou glândulas). Nervos mistos contêm tanto fibras sensitivas quanto motoras.
O sistema nervoso autônomo
Algumas das atividades do sistema nervoso, como o pensamento e o controle dos movimentos, são muito óbvias para nós. Mas o sistema nervoso também está trabalhando, sem que o percebamos, no controle dos órgãos internos.
Esta é a responsabilidade de uma parte especial do sistema nervoso chamada sistema nervoso autônomo, que regula a circulação sanguínea, a digestão, a respiração, os órgãos reprodutores e a eliminação dos resíduos do organismo. Também controla glândulas importantes que têm efeitos poderosos sobre o corpo. O sistema nervoso autônomo trabalha independentemente da maior parte do cérebro e suas células estão agrupadas em gânglios próximos da coluna vertebral. Ele opera inteiramente por reflexos e, embora o tronco cerebral também esteja envolvido em suas atividades, não temos consciência disso.

Esse sistema está dividido em duas partes, o sistema nervoso simpático e parassimpático, que trabalham um em oposição ao outro. Um dos sistemas estimulam um órgão, uma glândula, por exemplo, fazendo-a trabalhar bastante, o outro sistema faz cessar esse trabalho. Primeiro um começa; depois o outro, e o resultado é que o órgão é mantido trabalhando no nível correto.
O trabalho do sistema nervoso simpático pode ser observado quando estamos bravos ou assustados; sua ação faz o coração bater mais rápido e a respiração tornar-se mais profunda. As pupilas dos olhos dilatam-se e nos tornamos pálidos à medida que o sangue é drenado da pele para alimentar os músculos de que podemos precisar para uma reação qualquer. Isso tudo acontece porque o sistema simpático foi, acionado, fazendo o corpo ficar pronto para uma emergência.
As funções do córtex
Os músculos dos nossos órgãos internos trabalham automaticamente, mas a maioria dos nossos músculos trabalham apenas quando queremos movê-los. Estes são os músculos voluntários. Os movimentos voluntários, como caminhar, mover os braços ou usar os dedos, são diretamente controlados pelo cérebro. Uma estreita faixa de córtex que atravessa o topo de nosso cérebro, chamado de córtex motor, está em ligação direta com os nossos movimentos. O córtex motor recolhe informações de outras partes do cérebro, incluindo os sinais dos órgãos dos sentidos. Quando a decisão de mover um músculo ou uma série de músculos é tomada, o córtex transmite suas instruções para a parte apropriada do corpo.
Partes diferentes do córtex motor têm funções especiais, cada uma controlando os movimentos de certas partes do corpo. Partes importantes e complexas, tais como mãos e lábios, requerem um controle muito cuidadoso e os muitos neurônios necessários para esse trabalho ocupam grandes áreas do córtex. Partes menos complicadas precisam de menos controle e, portanto, há áreas menores de córtex destinadas a elas. Da mesma maneira que o movimento é controlado pelo córtex motor, partes especiais do córtex sensorial são responsáveis pelo tato. Outras partes cuidam da visão, da audição e de todos os outros sentidos.
Onde ocorre o pensamento
O movimento e os sentidos ocupam apenas duas estreitas faixas transversais do córtex cerebral. O resto do córtex não tem funções tão facilmente reconhecíveis. Contém as áreas de associação, e é onde, provavelmente, ocorre o pensamento. Por "pensamento", queremos dizer o exame e a interpretação do enorme número de sinais que chegam ao cérebro, e a decisão de qualquer ação a ser efetuada - ou, às vezes, a decisão de não agir. Algumas funções, entre elas a fala, estão espalhadas pelo córtex em pequenas áreas. A fala é também controlada por várias áreas diferentes do cérebro, além de uma parte do córtex.
A maneira pela qual as áreas de associação trabalham ainda não é bem compreendida. Algumas vezes grandes partes do cérebro podem ser afetadas, por doença ou por acidente, sem provocar muitos problemas; por outro lado, danos em pequenas partes podem originar graves distúrbios. Na realidade, a maneira pela qual o cérebro funciona é muito mais complicada do que parece à primeira vista. Partes muito grandes do cérebro parecem não ter nenhuma finalidade aparente, mas, como os neurônios estão de tal maneira interligados, acredita-se que todas as partes do cérebro têm alguma função. Talvez parte dessa "reserva" cerebral comece a ser usada para substituir os neurônios que vão morrendo à medida que envelhecemos.
www.sobiologia.com.br
Conjuntos
Conjunto é uma reunião de elementos, podemos dizer que essa definição é bem primitiva, mas a partir dessa ideia podemos relacionar outras situações. O conjunto universo e o conjunto vazio são tipos especiais de conjuntos.
Vazio: não possui elementos e pode ser representado por { } ou Ø.
Universo: possui todos os elementos de acordo com o que estamos trabalhando, pode ser representado pela letra maiúscula U.
Representando conjuntos
A representação de um conjunto depende de determinadas condições:
Exemplo 1
Condição: O conjunto dos números pares maiores que zero e menores que quinze.Representação através de seus elementos.
A = {2, 4, 6, 8, 10, 12, 14}
Representação pela propriedade de seus elementos.
A = {x / x é par e 0 < x < 15}, o símbolo da barra (/) significa “tal que”.
x tal que x é par e x maior que zero e x menor que 15.
Exemplo 2
Condição: O conjunto dos números Naturais ímpares menores que vinte.Elementos
A = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}
Propriedade dos elementos
A = {x Є N / x é impar e x < 20}
x pertence aos naturais tal que x é impar menor que 20.
Outra forma de representação de conjuntos de elementos é a utilização de diagramas. Observe os conjuntos A e B.
A = {x / 2 < x ≤ 12} e B = {x / 4 < x < 8}

Vazio: não possui elementos e pode ser representado por { } ou Ø.
Universo: possui todos os elementos de acordo com o que estamos trabalhando, pode ser representado pela letra maiúscula U.
Representando conjuntos
A representação de um conjunto depende de determinadas condições:
Exemplo 1
Condição: O conjunto dos números pares maiores que zero e menores que quinze.Representação através de seus elementos.
A = {2, 4, 6, 8, 10, 12, 14}
Representação pela propriedade de seus elementos.
A = {x / x é par e 0 < x < 15}, o símbolo da barra (/) significa “tal que”.
x tal que x é par e x maior que zero e x menor que 15.
Exemplo 2
Condição: O conjunto dos números Naturais ímpares menores que vinte.Elementos
A = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}
Propriedade dos elementos
A = {x Є N / x é impar e x < 20}
x pertence aos naturais tal que x é impar menor que 20.
Outra forma de representação de conjuntos de elementos é a utilização de diagramas. Observe os conjuntos A e B.
A = {x / 2 < x ≤ 12} e B = {x / 4 < x < 8}

União do conjunto A com o conjunto B. (A U B)


Os conjuntos servem para representar qualquer situação envolvendo ou não elementos. Na Matemática, uma importante aplicação dos conjuntos é na representação de conjuntos numéricos.
Conjunto dos números Naturais
Conjunto dos números Inteiros
Conjunto dos números Racionais
Conjunto dos números Irracionais
Conjunto dos números Reais
Conjunto dos números Complexos
Conjunto dos números Algébricos
Conjunto dos números Transcendentais
Conjunto dos números Imaginários
Os estudos básicos sobre conjuntos deram origem aos estudos relacionados às Teorias dos Conjuntos, que faz uma análise sobre as suas propriedades. Esses estudos se originaram nos trabalhos do matemático russo Georg Cantor. Na teoria dos conjuntos, os elementos podem ser: pessoas, números, outros conjuntos, dados estatísticos e etc.
Marcos Noé
Conjunto dos números Naturais
Conjunto dos números Inteiros
Conjunto dos números Racionais
Conjunto dos números Irracionais
Conjunto dos números Reais
Conjunto dos números Complexos
Conjunto dos números Algébricos
Conjunto dos números Transcendentais
Conjunto dos números Imaginários
Os estudos básicos sobre conjuntos deram origem aos estudos relacionados às Teorias dos Conjuntos, que faz uma análise sobre as suas propriedades. Esses estudos se originaram nos trabalhos do matemático russo Georg Cantor. Na teoria dos conjuntos, os elementos podem ser: pessoas, números, outros conjuntos, dados estatísticos e etc.
Equação do Segundo Grau
EQUAÇÃO DO 2° GRAU
A fórmula quadrática de Sridhara (Bhaskara)
Mostraremos na sequência como o matemático Sridhara, obteve a Fórmula (conhecida como sendo) de Bhaskara, que é a fórmula geral para a resolução de equações do segundo grau. Um fato curioso é que a Fórmula de Bhaskara não foi descoberta por ele mas pelo matemático hindu Sridhara, pelo menos um século antes da publicação de Bhaskara, fato reconhecido pelo próprio Bhaskara, embora o material construído pelo pioneiro não tenha chegado até nós.
O fundamento usado para obter esta fórmula foi buscar uma forma de reduzir a equação do segundo grau a uma do primeiro grau, através da extração de raízes quadradas de ambos os membros da mesma.
Seja a equação:
ax² + bx + c = 0
onde os números reais a, b e c são os coeficientes da equação, sendo que a deve ser diferente de zero. Essa equação é também chamada de equação quadrática, pois o termo de maior grau está elevado ao quadrado
Equação Completa do segundo grau
Uma equação do segundo grau é completa, se todos os coeficientes a, b e c são diferentes de zero.
Exemplos:
1) 2 x² + 7x + 5 = 0
2) 3 x² + x + 2 = 0
o coeficiente a é diferente de zero.
Exemplos:
1) 4 x² + 6x = 0
2) 3 x² + 9 = 0
3) 2 x² = 0
Resolução de equações completas do 2° grau
Como vimos, uma equação do tipo: ax²+bx+c=0, é uma equação completa do segundo grau e para resolvê-la basta usar a fórmula quadrática (atribuída a Bhaskara), que pode ser escrita na forma:
onde Δ=b²-4ac é o discriminante da equação.Para esse discriminante Δ, há três possíveis situações:
1) Δ <> 0, há duas soluções reais e diferentes
Mostraremos agora como usar a fórmula de Bhaskara para resolver a equação:
x² - 5 x + 6 = 0
1) Identificar os coeficientes: a=1, b= -5, c=6
2) Escrever o discriminante Δ = b²-4ac.
3) Calcular Δ=(-5)²-4×1×6=25-24=1
4) Escrever a fórmula de Bhaskara:
EXERCÍCIOS
1. Calcular o discriminante de cada equação e analisar as raízes em cada caso:
a) x² + 9 x + 8 = 0 (R:-1 e -8)
b) 9 x² - 24 x + 16 = 0 (R:4/3)
c) x² - 2 x + 4 = 0 (vazio)
d) 3 x² - 15 x + 12 = 0 (R: 1 e 4)
e) 10 x² + 72 x - 64 = 0 (R:-8 e 4/5)
e) 5x² - 3x - 2 = 0
f) x² - 10x + 25 = 0
g) x² - x - 20 = 0
h) x² - 3x -4 = 0
i) x² - 8x + 7 = 0
RESOLVA AS EQUAÇÕES DE 2º GRAU
1) x² - 5x + 6 = 0 _____(R:2,3)
2) x² - 8x + 12 = 0 ______(R:2,6)
3) x² + 2x - 8 = 0______ (R:2,-4)
4) x² - 5x + 8 = 0 ______(R:vazio)
5) 2x² - 8x + 8 = 0_______ (R:2,)
6) x² - 4x - 5 = 0_______ (R:-1, 5)
7) -x² + x + 12 = 0_______ (R:-3, 4)
8) -x² + 6x - 5 = 0_______ (R:1,5)
9) 6x² + x - 1 = 0______ (R:1/3 , -1/2)
10) 3x² - 7x + 2 = 0 ______(R:2, 1/3)
11) 2x² - 7x = 15 _______(R:5, -3/2)
12) 4x² + 9 = 12x______ (R:3/2)
13) x² = x + 12 ______(R:-3 , 4)
14) 2x² = -12x - 18 _____(R:-3 )
15) x² + 9 = 4x_____ (R: vazio)
16) 25x² = 20x – 4 ____(R: 2/5)
17) 2x = 15 – x² ______(R: 3 , -5)
18) x² + 3x – 6 = -8____ (R:-1 , -2)
19) x² + x – 7 = 5 ____(R: -4 , 3)
20) 4x² - x + 1 = x + 3x² ___(R: 1)
21) 3x² + 5x = -x – 9 + 2x²____ (R: -3)
22) 4 + x ( x - 4) = x _____(R: 1,4)
23) x ( x + 3) – 40 = 0 _____(R: 5, -8)
24) x² + 5x + 6 = 0 _____(R:-2,-3)
25) x² - 7x + 12 = 0 _____(R:3,4)
26) x² + 5x + 4 = 0 _____(R:-1,-4)
27) 7x² + x + 2 = 0 _____(vazio)
28) x² - 18x + 45 = 0 _____(R:3,15)
29) -x² - x + 30 = 0 _____(R:-6,5)
30) x² - 6x + 9 = 0 _____(R:3)
31) ( x + 3)² = 1_______(R:-2,-4)
32) ( x - 5)² = 1_______(R:3,7)
33)( 2x - 4)² = 0_______(R:2)
34) ( x - 3)² = -2x²_______(R:vazio)
35)Na equação 3x² - 12 = 0 as soluções são:
a)0 e 1
b)-1 e 1
c)-2 e 2 (x)
d)-3 e 3
e)0 e 4
36) x² + 3x - 28 = 0 (R: -7,4)
37) 3x² - 4x + 2 = 0 (R: vazio)
38) x² - 3 = 4x + 2 (R: -1,5)
PROBLEMAS COM EQUAÇÃO DO 2° GRAU
1) A soma de um numero com o seu quadrado é 90. Calcule esse numero. (R:9 e-10)
2) A soma do quadrado de um número com o próprio número é 12. Calcule esse numero (R: 3 e -4)
3) O quadrado menos o dobro de um número é igual a -1. Calcule esse número. (R:1)
4) A diferença entre o quadrado e o dobro de um mesmo número é 80. Calcule esse número (R:10 e -8)
5) O quadrado de um número aumentado de 25 é igual a dez vezes esse número. Calcule esse número (R: 5)
6) A soma do quadrado de um número com o seu triplo é igual a 7 vezes esse número. Calcule esse número.(R: 0 e 4)
7) O quadrado menos o quádruplo de um numero é igual a 5. Calcule esse número (R: 5 e -1)
8) O quadrado de um número é igual ao produto desse número por 3, mais 18. Qual é esse numero? (R: 6 e -3)
9) O dobro do quadrado de um número é igual ao produto desse numero por 7 menos 3. Qual é esse numero? (R:3 e ½)
10) O quadrado de um número menos o triplo do seu sucessivo é igual a 15. Qual é esse numero?(R: 6 e -3)
11) Qual o número que somado com seu quadrado resulta em 56? (R:-8 e 7)
12) Um numero ao quadrado mais o dobro desse número é igual a 35. Qual é esse número ? (R:-7 e 5)
13) O quadrado de um número menos o seu triplo é igual a 40. Qual é esse número? (R:8 e -5)
14) Calcule um número inteiro tal que três vezes o quadrado desse número menos o dobro desse número seja igual a 40. (R:4)
15) Calcule um número inteiro e positivo tal que seu quadrado menos o dobro desse número seja igual a 48. (R:8)
16) O triplo de um número menos o quadrado desse número é igual a 2. Qual é esse número? (R:1 e 2)
17) Qual é o número , cujo quadrado mais seu triplo é igual a 40? ( R: 5 , -8)
18) O quadrado de um número diminuido de 15 é igual ao seu dobro. Calcule esse número.
(R: 5 e -3)
19) Determine um número tal que seu quadrado diminuído do seu triplo é igual a 26. (R:7 e -4)
20) Se do quadrado de um número, negativo subtraimos 7, o resto será 42. Qual é esse número?
(R: -7)
21) A diferença entre o dobro do quadrado de um número positivo e o triplo desse número é 77. Calcule o número. (R: 7)
22) Determine dois números ímpares consecutivos cujo produto seja 143. (R: 11 e 13 ou -11, -13)
23) Um azulejista usou 2000 azulejos quadrados e iguais para revestir 45m² de parede. Qual é a medida do lado de cada azulejo? (R:15 cm)
RESOLUÇÃO DE EQUAÇÃO INCOMPLETAS
Resolver uma equação é determinar todas as suas soluções. Vejamos, através de exemplos, como se resolvem as equações incompletas do 2° grau
1° CASO – equações da forma ax² + c = 0, (b = 0)
Exemplos:
1) x² - 25 = 0
x² = 25
x = √25
x = 5
logo V= (+5 e -5)
2) 2x² - 18 = 0
2x² = 18
x² = 18/2
x² = 9
x = √9
x = 3
logo V= (-3 e +3)
3) 7x² - 14 = 0
7x² = 14
x² = 14/7
x² = 2
x = √2
logo V = (-√2 e +√2)
4) x²+ 25 = 0
x² = -25
x = √-25
obs: não existe nenhum número real que elevado ao quadrado seja igual a -25
EXERCÍCIOS
1) Resolva as seguintes equações do 2° grau
a) x² - 49 = 0 (R: -7 e +7)
b) x² = 1 (R: +1 e -1)
c) 2x² - 50 = 0 (R: 5 e -5)
d) 7x² - 7 = 0 (R: 1 e -1)
e) 5x² - 15 = 0 (R: √3 e -√3)
f) 21 = 7x² (R: √3 e -√3)
g) 5x² + 20 = 0 (R: vazio)
h) 7x² + 2 = 30 (R: 2 e -2 )
i) 2x² - 90 = 8 (R: 7 e -7)
j) 4x² - 27 = x² (R:3 e -3)
k) 8x² = 60 – 7x² (R: 2 e -2)
l) 3(x² - 1 ) = 24 (R: 3 e -3)
m) 2(x² - 1) = x² + 7 (R:3 e -3)
n) 5(x² - 1) = 4(x² + 1) (R:3 e -3)
o) (x – 3)(x + 4) + 8 = x (R:2 e -2)
2° CASO: Equações da forma ax² + bx = 0 ( c = 0)
Propriedade: Para que um produto seja nulo é preciso que um dos fatores seja zero .
Exemplos
1) resolver x² - 5x = 0
fatorando x ( x – 5) = 0
deixando um dos fatores nulo temos x = 0
e o outro x – 5 = 0 , passando o 5 para o outro lado do igual temos x = 5
logo V= (0 e 5)
2) resolver: 3x² - 10x = 0
fatorando: x (3x – 10) = 0
deixando um dos fatores nulo temos x = 0
Tendo também 3x – 10 = 0
3x = 10
x = 10/3
logo V= (0 e 10/3)
Observe que, nesse caso, uma das raízes é sempre zero.
EXERCÍCIOS
1) Resolva as seguintes equações do 2° grau.
a) x² - 7x = 0 (R: 0 e 7)
b) x² + 5x = 0 (R: 0 e -5)
c) 4x² - 9x = 0 (R: 0 e 9/4)
d) 3x² + 5x =0 (R: 0 e -5/3)
e) 4x² - 12x = 0 (R: 0 e 3)
f) 5x² + x = 0 (R: 0 e -1/5)
g) x² + x = 0 (R: 0 e -1)
h) 7x² - x = 0 (R: 0 e 1/7)
i) 2x² = 7x (R: 0 e 7/2)
j) 2x² = 8x (R: 0 e 4)
k) 7x² = -14x (R: 0 e -2)
l) -2x² + 10x = 0 (R: 0 e 5)
2) Resolva as seguintes equações do 2° grau
a) x² + x ( x – 6 ) = 0 (R: 0 e 3)
b) x(x + 3) = 5x (R: 0 e 2)
c) x(x – 3) -2 ( x-3) = 6 (R: 0 e 5)
d) ( x + 5)² = 25 (R: 0 e -10)
e) (x – 2)² = 4 – 9x (R: 0 e -5)
f) (x + 1) (x – 3) = -3 (R: 0 e 2)
A fórmula quadrática de Sridhara (Bhaskara)
Mostraremos na sequência como o matemático Sridhara, obteve a Fórmula (conhecida como sendo) de Bhaskara, que é a fórmula geral para a resolução de equações do segundo grau. Um fato curioso é que a Fórmula de Bhaskara não foi descoberta por ele mas pelo matemático hindu Sridhara, pelo menos um século antes da publicação de Bhaskara, fato reconhecido pelo próprio Bhaskara, embora o material construído pelo pioneiro não tenha chegado até nós.
O fundamento usado para obter esta fórmula foi buscar uma forma de reduzir a equação do segundo grau a uma do primeiro grau, através da extração de raízes quadradas de ambos os membros da mesma.
Seja a equação:
ax² + bx + c = 0
onde os números reais a, b e c são os coeficientes da equação, sendo que a deve ser diferente de zero. Essa equação é também chamada de equação quadrática, pois o termo de maior grau está elevado ao quadrado
Equação Completa do segundo grau
Uma equação do segundo grau é completa, se todos os coeficientes a, b e c são diferentes de zero.
Exemplos:
1) 2 x² + 7x + 5 = 0
2) 3 x² + x + 2 = 0
o coeficiente a é diferente de zero.
Exemplos:
1) 4 x² + 6x = 0
2) 3 x² + 9 = 0
3) 2 x² = 0
Resolução de equações completas do 2° grau
Como vimos, uma equação do tipo: ax²+bx+c=0, é uma equação completa do segundo grau e para resolvê-la basta usar a fórmula quadrática (atribuída a Bhaskara), que pode ser escrita na forma:
onde Δ=b²-4ac é o discriminante da equação.Para esse discriminante Δ, há três possíveis situações:
1) Δ <> 0, há duas soluções reais e diferentes
Mostraremos agora como usar a fórmula de Bhaskara para resolver a equação:
x² - 5 x + 6 = 0
1) Identificar os coeficientes: a=1, b= -5, c=6
2) Escrever o discriminante Δ = b²-4ac.
3) Calcular Δ=(-5)²-4×1×6=25-24=1
4) Escrever a fórmula de Bhaskara:
EXERCÍCIOS
1. Calcular o discriminante de cada equação e analisar as raízes em cada caso:
a) x² + 9 x + 8 = 0 (R:-1 e -8)
b) 9 x² - 24 x + 16 = 0 (R:4/3)
c) x² - 2 x + 4 = 0 (vazio)
d) 3 x² - 15 x + 12 = 0 (R: 1 e 4)
e) 10 x² + 72 x - 64 = 0 (R:-8 e 4/5)
e) 5x² - 3x - 2 = 0
f) x² - 10x + 25 = 0
g) x² - x - 20 = 0
h) x² - 3x -4 = 0
i) x² - 8x + 7 = 0
RESOLVA AS EQUAÇÕES DE 2º GRAU
1) x² - 5x + 6 = 0 _____(R:2,3)
2) x² - 8x + 12 = 0 ______(R:2,6)
3) x² + 2x - 8 = 0______ (R:2,-4)
4) x² - 5x + 8 = 0 ______(R:vazio)
5) 2x² - 8x + 8 = 0_______ (R:2,)
6) x² - 4x - 5 = 0_______ (R:-1, 5)
7) -x² + x + 12 = 0_______ (R:-3, 4)
8) -x² + 6x - 5 = 0_______ (R:1,5)
9) 6x² + x - 1 = 0______ (R:1/3 , -1/2)
10) 3x² - 7x + 2 = 0 ______(R:2, 1/3)
11) 2x² - 7x = 15 _______(R:5, -3/2)
12) 4x² + 9 = 12x______ (R:3/2)
13) x² = x + 12 ______(R:-3 , 4)
14) 2x² = -12x - 18 _____(R:-3 )
15) x² + 9 = 4x_____ (R: vazio)
16) 25x² = 20x – 4 ____(R: 2/5)
17) 2x = 15 – x² ______(R: 3 , -5)
18) x² + 3x – 6 = -8____ (R:-1 , -2)
19) x² + x – 7 = 5 ____(R: -4 , 3)
20) 4x² - x + 1 = x + 3x² ___(R: 1)
21) 3x² + 5x = -x – 9 + 2x²____ (R: -3)
22) 4 + x ( x - 4) = x _____(R: 1,4)
23) x ( x + 3) – 40 = 0 _____(R: 5, -8)
24) x² + 5x + 6 = 0 _____(R:-2,-3)
25) x² - 7x + 12 = 0 _____(R:3,4)
26) x² + 5x + 4 = 0 _____(R:-1,-4)
27) 7x² + x + 2 = 0 _____(vazio)
28) x² - 18x + 45 = 0 _____(R:3,15)
29) -x² - x + 30 = 0 _____(R:-6,5)
30) x² - 6x + 9 = 0 _____(R:3)
31) ( x + 3)² = 1_______(R:-2,-4)
32) ( x - 5)² = 1_______(R:3,7)
33)( 2x - 4)² = 0_______(R:2)
34) ( x - 3)² = -2x²_______(R:vazio)
35)Na equação 3x² - 12 = 0 as soluções são:
a)0 e 1
b)-1 e 1
c)-2 e 2 (x)
d)-3 e 3
e)0 e 4
36) x² + 3x - 28 = 0 (R: -7,4)
37) 3x² - 4x + 2 = 0 (R: vazio)
38) x² - 3 = 4x + 2 (R: -1,5)
PROBLEMAS COM EQUAÇÃO DO 2° GRAU
1) A soma de um numero com o seu quadrado é 90. Calcule esse numero. (R:9 e-10)
2) A soma do quadrado de um número com o próprio número é 12. Calcule esse numero (R: 3 e -4)
3) O quadrado menos o dobro de um número é igual a -1. Calcule esse número. (R:1)
4) A diferença entre o quadrado e o dobro de um mesmo número é 80. Calcule esse número (R:10 e -8)
5) O quadrado de um número aumentado de 25 é igual a dez vezes esse número. Calcule esse número (R: 5)
6) A soma do quadrado de um número com o seu triplo é igual a 7 vezes esse número. Calcule esse número.(R: 0 e 4)
7) O quadrado menos o quádruplo de um numero é igual a 5. Calcule esse número (R: 5 e -1)
8) O quadrado de um número é igual ao produto desse número por 3, mais 18. Qual é esse numero? (R: 6 e -3)
9) O dobro do quadrado de um número é igual ao produto desse numero por 7 menos 3. Qual é esse numero? (R:3 e ½)
10) O quadrado de um número menos o triplo do seu sucessivo é igual a 15. Qual é esse numero?(R: 6 e -3)
11) Qual o número que somado com seu quadrado resulta em 56? (R:-8 e 7)
12) Um numero ao quadrado mais o dobro desse número é igual a 35. Qual é esse número ? (R:-7 e 5)
13) O quadrado de um número menos o seu triplo é igual a 40. Qual é esse número? (R:8 e -5)
14) Calcule um número inteiro tal que três vezes o quadrado desse número menos o dobro desse número seja igual a 40. (R:4)
15) Calcule um número inteiro e positivo tal que seu quadrado menos o dobro desse número seja igual a 48. (R:8)
16) O triplo de um número menos o quadrado desse número é igual a 2. Qual é esse número? (R:1 e 2)
17) Qual é o número , cujo quadrado mais seu triplo é igual a 40? ( R: 5 , -8)
18) O quadrado de um número diminuido de 15 é igual ao seu dobro. Calcule esse número.
(R: 5 e -3)
19) Determine um número tal que seu quadrado diminuído do seu triplo é igual a 26. (R:7 e -4)
20) Se do quadrado de um número, negativo subtraimos 7, o resto será 42. Qual é esse número?
(R: -7)
21) A diferença entre o dobro do quadrado de um número positivo e o triplo desse número é 77. Calcule o número. (R: 7)
22) Determine dois números ímpares consecutivos cujo produto seja 143. (R: 11 e 13 ou -11, -13)
23) Um azulejista usou 2000 azulejos quadrados e iguais para revestir 45m² de parede. Qual é a medida do lado de cada azulejo? (R:15 cm)
RESOLUÇÃO DE EQUAÇÃO INCOMPLETAS
Resolver uma equação é determinar todas as suas soluções. Vejamos, através de exemplos, como se resolvem as equações incompletas do 2° grau
1° CASO – equações da forma ax² + c = 0, (b = 0)
Exemplos:
1) x² - 25 = 0
x² = 25
x = √25
x = 5
logo V= (+5 e -5)
2) 2x² - 18 = 0
2x² = 18
x² = 18/2
x² = 9
x = √9
x = 3
logo V= (-3 e +3)
3) 7x² - 14 = 0
7x² = 14
x² = 14/7
x² = 2
x = √2
logo V = (-√2 e +√2)
4) x²+ 25 = 0
x² = -25
x = √-25
obs: não existe nenhum número real que elevado ao quadrado seja igual a -25
EXERCÍCIOS
1) Resolva as seguintes equações do 2° grau
a) x² - 49 = 0 (R: -7 e +7)
b) x² = 1 (R: +1 e -1)
c) 2x² - 50 = 0 (R: 5 e -5)
d) 7x² - 7 = 0 (R: 1 e -1)
e) 5x² - 15 = 0 (R: √3 e -√3)
f) 21 = 7x² (R: √3 e -√3)
g) 5x² + 20 = 0 (R: vazio)
h) 7x² + 2 = 30 (R: 2 e -2 )
i) 2x² - 90 = 8 (R: 7 e -7)
j) 4x² - 27 = x² (R:3 e -3)
k) 8x² = 60 – 7x² (R: 2 e -2)
l) 3(x² - 1 ) = 24 (R: 3 e -3)
m) 2(x² - 1) = x² + 7 (R:3 e -3)
n) 5(x² - 1) = 4(x² + 1) (R:3 e -3)
o) (x – 3)(x + 4) + 8 = x (R:2 e -2)
2° CASO: Equações da forma ax² + bx = 0 ( c = 0)
Propriedade: Para que um produto seja nulo é preciso que um dos fatores seja zero .
Exemplos
1) resolver x² - 5x = 0
fatorando x ( x – 5) = 0
deixando um dos fatores nulo temos x = 0
e o outro x – 5 = 0 , passando o 5 para o outro lado do igual temos x = 5
logo V= (0 e 5)
2) resolver: 3x² - 10x = 0
fatorando: x (3x – 10) = 0
deixando um dos fatores nulo temos x = 0
Tendo também 3x – 10 = 0
3x = 10
x = 10/3
logo V= (0 e 10/3)
Observe que, nesse caso, uma das raízes é sempre zero.
EXERCÍCIOS
1) Resolva as seguintes equações do 2° grau.
a) x² - 7x = 0 (R: 0 e 7)
b) x² + 5x = 0 (R: 0 e -5)
c) 4x² - 9x = 0 (R: 0 e 9/4)
d) 3x² + 5x =0 (R: 0 e -5/3)
e) 4x² - 12x = 0 (R: 0 e 3)
f) 5x² + x = 0 (R: 0 e -1/5)
g) x² + x = 0 (R: 0 e -1)
h) 7x² - x = 0 (R: 0 e 1/7)
i) 2x² = 7x (R: 0 e 7/2)
j) 2x² = 8x (R: 0 e 4)
k) 7x² = -14x (R: 0 e -2)
l) -2x² + 10x = 0 (R: 0 e 5)
2) Resolva as seguintes equações do 2° grau
a) x² + x ( x – 6 ) = 0 (R: 0 e 3)
b) x(x + 3) = 5x (R: 0 e 2)
c) x(x – 3) -2 ( x-3) = 6 (R: 0 e 5)
d) ( x + 5)² = 25 (R: 0 e -10)
e) (x – 2)² = 4 – 9x (R: 0 e -5)
f) (x + 1) (x – 3) = -3 (R: 0 e 2)
Ponto médio de um seguimento de reta
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Segmento de reta é limitado por dois pontos de uma reta. Por exemplo, considere a reta r e dois pontos A e B que pertencem a essa reta.
A distância dos pontos A e B é o segmento da reta r.
Por ser um “pedaço” de uma reta podemos medir o seu comprimento (distância entre dois pontos de uma reta), assim possuindo seu ponto médio (ponto que separa o segmento ao meio).
Se o ponto fosse A (2,1) e B (3,4), qual seria as coordenadas do ponto médio?
Utilizando o Teorema de Tales, podemos dizer que:
AM = A1M1
MB M1B1
Os segmentos AM e MB são iguais, pois M é o ponto médio de A e B, assim podemos escrever:
1 = A1M1
M1 B1
x A = 2, então A1M1 = xM – 2
x B = 3, então M1B1 = 3 – xM
Substituindo A1M1 = xM – 2 e M1B1 = 3 – xM em 1 = A1M1, teremos:
M1B1
1 = A1M1
M1B1
1 = xM – 2
3 – xM
xM – 2 = 3 – xM
2xM = 3 + 2
xM = 3+2
2
xM = 5/2
Podemos concluir que a abscissa xM é a media entre as abscissas xA e xB, portando yM será a mediana de yA e yB.
y M = 4 + 1 2
y M = 5/2
Portanto, o ponto médio M terá coordenadas iguais a (5/2, 5/2).
Assim, a forma geral para o cálculo das coordenadas de um ponto médio será:
xM = xA + xB
2
yM = yA + yB
2
Assinar:
Comentários (Atom)