Observe as figuras:
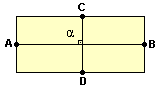
Figura A
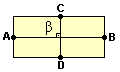
Figura B
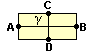
Figura C
Elas representam retângulos com escalas diferentes. Observe que os três retângulos tem a mesma forma, mas de tamanhos diferentes.Dizemos que esse mapas são figuras semelhantes.
Nessas figuras podemos identificar:
AB - distância entre A e B (comprimento do retângulo)
CD - distância entre C e D (largura do retângulo)
Medindo os segmentos de reta
| m ( | m ( | ângulo | |
| Fig. C | 3,9 cm | 1,3 cm | |
| Fig. B | 4,5 cm | 1,5 cm | |
| Fig. A | 6,0 cm | 2,0 cm |
- Os ângulos correspondente nas três figuras têm medidas iguais;
- As medidas dos segmentos correspondentes são proporcionais;
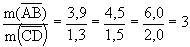
Desse exemplo, podemos concluir que duas ou mais figuras são semelhantes em geometria quando:
- os ângulos correspondentes têm medidas iguais ;
- as medidas dos segmentos correspondentes são proporcionais;
- os elementos das figuras são comuns.
Outro exemplos de figuras semelhantes:

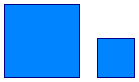
têm formas iguais e tamanhos diferentes.
Polígonos Semelhantes
Considere os polígonos ABCD e A'B'C'D', nas figuras:
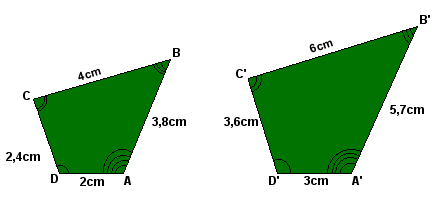
Observe que:
- os ângulos correspondentes são congruentes:
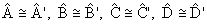
- os lados correspondentes (ou homólogos) são proporcionais:
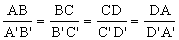
ou
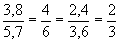
Podemos concluir que os polígonos ABCD e A'B'C'D' são semelhantes e indicamos:
ABCD ~ A'B'D'C' (lê-se "polígonos ABCD é semelhante ao polígono A'B'D'C' ")
ABCD ~ A'B'D'C' (lê-se "polígonos ABCD é semelhante ao polígono A'B'D'C' ")
Ou seja:
| Dois polígonos são semelhantes quando os ângulos correspondentes são congruentes e os lados correspondentes são proporcionais. |
A razão entre dois lados correspondentes em polígonos semelhante denomina-se razão de semelhança, ou seja:
A razão de semelhança dos polígonos considerados é 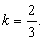
Obs: A definição de polígonos semelhantes só é válida quando ambas as condições são satisfeitas: Ângulos correspondentes congruentes e lados correspondentes proporcionais. Apenas uma das condições não é suficiente para indicar a semelhança entre polígonos.
Propriedades
| Se dois polígonos são semelhantes, então a razão entre seus perímetros é igual à razão entre as medidas de dois lados homólogos quaisquer dos polígonos. |
Demonstração:
Sendo ABCD ~ A'B'C'D', temos que:
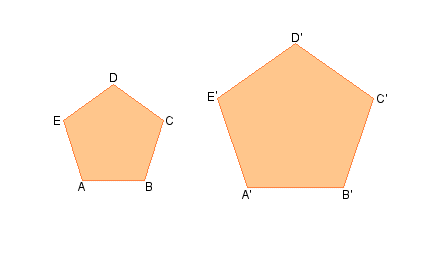
Os perímetros desses polígonos podem ser assim representados:
Perímetro de ABCDE (2p) = AB + BC + CD + DE + EA
Perímetro de A'B'C'D'E' (2p') = A'B' + B'C' + C'D' + D'E' + E'A'
Por uma propriedade das proporções, podemos afirmar que:
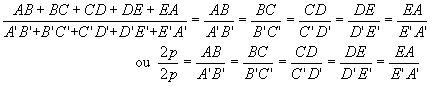
Perímetro de ABCDE (2p) = AB + BC + CD + DE + EA
Perímetro de A'B'C'D'E' (2p') = A'B' + B'C' + C'D' + D'E' + E'A'
Por uma propriedade das proporções, podemos afirmar que:
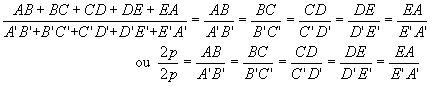
Exemplo:
- Os lados de um triângulo medem 3,6 cm, 6,4 cm e 8 cm. Esse triângulo é semelhante a um outro cujo perímetro mede 45 cm. calcule os lados do segundo triângulo.
Solução
Razão de semelhança =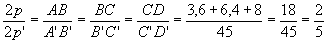
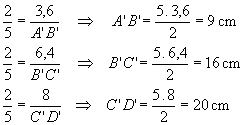
Razão de semelhança =
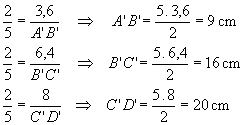
Logo, os lados do segundo triângulo são 9cm, 16cm e 20cm.
www.somatematica.com.br