Adição e subtração de números racionais aula 1

Sistema Muscular

Os músculos são órgãos constituídos principalmente por tecido muscular, especializado em contrair e realizar movimentos, geralmente em resposta a um estímulo nervoso.

Os músculos podem ser formados por três tipos básicos de tecido muscular:

Tecido Muscular Estriado Esquelético

Apresenta, sob observação microscópica, faixas alternadas transversais, claras e escuras. Essa estriação resulta do arranjo regular de microfilamentos formados pelas proteínas actina e miosina, responsáveis pela contração muscular. A célula muscular estriada chamada fibra muscular, possui inúmeros núcleos e pode atingir comprimentos que vão de 1mm a 60 cm.

Tecido Muscular Liso

Está presente em diversos órgãos internos (tubo digestivo, bexiga, útero etc) e também na parede dos vasos sanguíneos. As células musculares lisas são uninucleadas e os filamentos de actina e miosina se dispõem em hélice em seu interior, sem formar padrão estriado como o tecido muscular esquelético.

A contração dos músculos lisos é geralmente involuntária, ao contrário da contração dos músculos esqueléticos.

Tecido Muscular Estriado Cardíaco

Está presente no coração. Ao microscópio, apresenta estriação transversal. Suas células são uninucleadas e têm contração involuntária.

Sarcômeros

As fibras musculares esqueléticas tem o citoplasma repleto de filamentos longitudinais muito finos, (as miofibrilas) constituídas por microfilamentos das proteínas actina e miosina. A disposição regular dessas proteínas ao longo da fibra produz o padrão de faixas claras e escuras alternadas, típicas do músculo estriado.

As unidades de actina e miosina que se repetem ao longo da miofibrila são chamadas sarcômeros. As faixas mais extremas do sarcômero, claras, são denominadas banda I e contém filamentos de actina. A faixa central mais escura é a banda A, as extremidades desta são formadas por filamentos de actina e miosina sobrepostos, enquanto sua região mediana mais clara, (a banda H), contém miosina.

Teoria do deslizamento dos filamentos

Quando o músculo se contrai, as bandas I e H diminuem de largura. A contração muscular se dá pelo deslizamento dos filamentos de actina sobre os de miosina. Essa idéia é conhecida como teoria do deslizamento dos filamentos.

Nas pontas dos filamentos de miosina existem pequenas projeções, capazes de formar ligações com certos sítios dos filamentos de actina quando o músculo é estimulado. As projeções da miosina puxam os filamentos de actina como dentes de uma engrenagem, forçando-os a deslizar sobre os filamentos de miosina, o que leva ao encurtamento das miofibrilas e à conseqüente contração da fibra muscular.

Contração Muscular

O estímulo para a contração é geralmente um impulso nervoso que se propaga pela membrana das fibras musculares, atingindo o retículo sarcoplasmático (um conjunto de bolsas membranosas citoplasmáticas onde há cálcio armazenado), que libera íons de cálcio no citoplasma. Ao entrar em contato com as miofibrilas, o cálcio desbloqueia os sítios de ligação de actina, permitindo que se ligue a miosina, iniciando a contração muscular.

Assim que cessa o estímulo, o cálcio é rebombeado para o interior do retículo sarcoplasmático e cessa a contração muscular.

A energia para contração muscular é suprida por moléculas de ATP (produzidas durante a respiração celular). O ATP atua na ligação de miosina à actina, o que resulta na contração muscular. Mas a principal reserva de energia nas células musculares é a fosfocreatina, onde grupos de fosfatos, ricos em energia, são transferidos da fosfocreatina para o ADP, que se transforma em ATP. Quando o trabalho muscular é intenso, as células musculares repõem seus estoques de ATP e de fosfocreatina, intensificando a respiração celular, utilizando o glicogênio como combustível.

Tetania e Fadiga Muscular

A estimulação contínua faz com que o músculo atinja um grau máximo de contração, o músculo permanece contraído, condição conhecida como tetania. Uma tetania muito prolongada ocasiona a fadiga muscular. Um músculo fadigado, após se relaxar, perde por um certo tempo, a capacidade de se contrair. Pode ocorrer por deficiência de ATP, incapacidade de propagação do estímulo nervoso através da membrana celular ou acúmulo de ácido lático.

Antagonismo muscular

A movimentação de uma parte do corpo depende da ação de músculos que atuam antagonicamente. Por exemplo, a contração do músculo bíceps e o relaxamento do tríceps, provocam a flexão do membro superior.

Fibras musculares lentas e rápidas

As fibras musculares esqueléticas diferem quanto ao tempo que levam para se contrair, podendo levar um tempo de até 5 vezes maior do que as rápidas para se contrair.

As fibras musculares lentas estão adaptadas à realização de trabalho contínuo, possuem maior quantidade de mitocôndrias, maior irrigação sanguínea e grande quantidade de mioglobina, capaz de estocar gás oxigênio. As fibras rápidas, pobres em mioglobina, estão presentes em músculos adaptados à contrações rápidas e fortes.

Esses dois tipos de fibras podem ser diferenciados apenas ao microscópio por meio de corantes especiais.

Tônus muscular

Os músculos mantêm-se normalmente em um estado de contração parcial, o tônus muscular, que é causado pela estimulação nervosa, e é um processo inconsciente que mantém os músculos preparados para entrar em ação. Quando o nervo que estimula um músculo é cortado, este perde tônus e se torna flácido. Estados de tensão emocional podem aumentar o tônus muscular, causando a sensação física de tensão muscular. Nesta condição, gasta mais energia que o normal e isso causa a fadiga.

Amapá

Bandeira do Amapá

Significado da bandeira: o azul simboliza a justiça e o céu amapaense; o verde representa as matas, além da esperança, o futuro, o amor e a liberdade; o amarelo, as riquezas do subsolo; o branco, a paz; o preto é uma homenagem aos que morreram lutando pelo estado.

O Amapá é um estado brasileiro que integra a Região Norte. Seu território, localizado no extremo norte do Brasil e banhado pelo oceano Atlântico, limita-se ao sul com o Pará, a noroeste com o Suriname e, por meio do rio Oiapoque, faz fronteira com a Guiana Francesa.

Com extensão territorial de 142.814,585 quilômetros quadrados, o Amapá é o menor estado nortista. Sua área abriga 16 municípios, cuja capital é a cidade de Macapá. Conforme dados divulgados em 2010 pelo Instituto Brasileiro de Geografia e Estatística (IBGE), a população estadual é composta por 668.689 habitantes, sendo a densidade demográfica de 4,6 habitantes por quilômetro quadrado. A taxa de crescimento demográfico é uma das maiores do país: 5,7% ao ano.

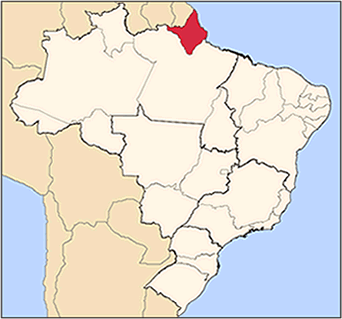
Localização do Amapá no mapa do Brasil

A floresta Amazônica cobre aproximadamente 90% do território amapaense, que também abriga mangues litorâneos e campos. O clima predominante é o equatorial. O relevo, por sua vez, é marcado por planície, depressão e algumas regiões de planaltos residuais. A rede hidrográfica é representada pelos rios Amazonas, Araguari, Jari, Maracá e Oiapoque.

O Amapá apresenta desenvolvimento econômico muito recente e enfrenta problemas em infraestrutura, sobretudo de transporte, comunicação e energia. O estado destaca-se por ser grande produtor de manganês, além de abrigar jazidas de ouro e caulim. Na agropecuária, os destaques são os cultivos de frutas, milho, arroz e feijão e a criação de búfalos. A pesca e o extrativismo vegetal são outras importantes atividades para a captação de recursos financeiros.

A qualidade de vida da população amapaense é a melhor da Região Norte, visto que o estado detém o maior Índice de Desenvolvimento Humano (IDH) desse complexo regional. A taxa de mortalidade infantil é de 23,2 para cada mil nascidos vivos, estando um pouco abaixo da média nacional, que é de 23,3. O analfabetismo atinge apenas 4% dos habitantes (a média brasileira é de 10%). Porém, existe um grande déficit nos serviços de saneamento ambiental – apenas 37% das residências possuem acesso à rede de esgoto.

Confira nossos artigos sobre o Amapá e conheça mais sobre os aspectos físicos, populacionais e econômicos dessa unidade federativa do Brasil.

alunosonline

Lobo-guará Maior canídeo sul-americano está em risco de extinção

Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso

Colégio Estadual Dinah Gonçalves

email accbarroso@hotmail.com        

 www.ensinodematemtica.blogspot.com.br

www.accbarrosogestar.blogspot.com.br 

www.youtube.com/accbarroso1

Lobo-guará: mais uma espécie que pode se extinguir
Muita gente já ouviu falar neste animal maravilhoso. Mas a maior parte do que se pensa sobre ele não condiz com a realidade. O lobo-guará (Chrysocyon brachyurus) é o maior e mais belo canídeo selvagem brasileiro e o mais alto do mundo. Última espécie de seu gênero, o lobo-guará possui pelagem vermelho-ouro, focinho preto, pernas longas e pretas e grandes orelhas apontadas para cima. A extremidade da cauda é mais clara que o resto do corpo.

Um lobo-guará adulto pode ter até 80 cm de altura (das patas às pontas das orelhas), 2 m da ponta da cauda até o focinho e pesar até 25 kg - sim, trata-se de um canídeo esbelto!

Lobo-guará não é lobo
Apesar de seu nome, o guará não é lobo e há muitas diferenças entre essas duas espécies. Seu grau de parentesco com os canídeos lupinos se estende até a família Canidae. A partir daí, o gênero muda (o lobo é do gênero Canis e o guará é pertence ao Chrysocyon).

Esses animais são tão diferentes em termos genéticos que um cruzamento entre guará e lobo não produziria filhotes. Para se fazer uma idéia do quanto esse fato determina um parentesco, se um cachorro (Canis familiaris) acasalar com um lobo (Canis lupus), nascerão filhotes - tanto o cão como o lobo pertencem ao mesmo gênero.

Enquanto os lobos vivem em matilhas e mantêm relações sociais complexas entre si, os guará vivem sozinhos. A exceção é a época de acasalamento, quando são encontrados aos pares. Mais: o Canis lupus é apenas carnívoro. Já o Chrysocyon brachyurus é onívoro (alimenta-se de frutos, insetos e pequenos mamíferos).

O lobo-guará é agressivo?
Muita gente pensa que os lobos-guará são implacáveis comedores de galinhas. Há até mesmo quem acredite que esses animais atacam as pessoas. Entra-se nesse momento em um assunto delicado.

Os lobos-guará não atacam seres humanos. De temperamento tímido e arredio, apenas rosnam quando acuados e ameaçam avançar para proteger seus filhotes. Esses canídeos podem desenvolver um relacionamento amistoso com seres humanos, como acontece em uma estação da Companhia Elétrica de Minas Gerais (Cemig). Nesse lugar, todas as noites, os funcionários recebem visitas de uma fêmea de lobo-guará e a presenteiam com petiscos.

Alimentação do lobo-guará
Um estudo publicado na revista científica Fapesp, realizado pelo pesquisador e professor do Instituto de Biociências da Universidade de São Paulo, José Carlos Motta Júnior, mostrou que a dieta dos lobos-guará divide-se em 50% de animais e 50% de frutos.

Dos animais predados por eles, apenas 1,9% correspondem aos galináceos. E tem mais: para cada galinha, esse canídeo mata de 50 a 70 ratos. Isso comprova sua importância no controle populacional desses animais (e como conseqüência, para a saúde humana).

Além disso, o Chrysocyon brachyurus é um importante dispersor das sementes dos frutos típicos do Cerrado - principalmente a lobeira e a gabiroba (Campomanesia spp).

Raiva (hidrofobia)
Todos temem a raiva, ou hidrofobia. E o lobo-guará pode, sim, contrair raiva. Essa doença o atinge por causa da atitude irresponsável dos seres humanos que abandonam cachorros em reservas e parques de preservação. Não fosse por isso, o lobos-guará não seriam contagiados.

Como todo animal quando está raivoso, o maior canídeo sul-americano apresenta comportamento anormal. A boa notícia é que há programas de vacinação para os lobos-guará - especialmente nas áreas em que o contato com as pessoas é maior. Mesmo assim, é bom evitar interagir com eles. Deixar animais selvagens em paz é uma forma de evitar acidentes.

Ameaça de extinção
O lobo-guará habitava o leste da Bolívia, o norte da Argentina, o Paraguai e a região Centro-Oeste do Brasil. Devido à caça predatória e a destruição progressiva de seu habitat natural, o canídeo mais alto do mundo está extinto nas três primeiras regiões citadas.

Ele ainda existe no Brasil e luta para sobreviver. A degradação ambiental continua a ameaçá-lo, bem como a caça ilegal. As previsões são de que nosso "lobo" deixe de existir em menos de 100 anos.

Lobo-guará em cativeiro
Há quem acredite que os zoológicos são uma esperança de preservação. Mas um lobo-guará confinado em uma jaula é uma triste visão. Esses animais são exímios andarilhos noturnos e sua "jaula" na natureza tem, de 30 a 110 km2. Essa é a área que um casal de lobos-guará ocupa e precisa para viver.

Proibido de andar, correr e caçar, os músculos das longas pernas se atrofiam. O animal pode perder a visão ou, ainda, morrer vítima de depressão. As melhores maneiras de salvar o lobo-guará, segundo ecólogos e biólogos, são a conscientização das pessoas, e a educação ambiental para as crianças.

Para saber mais, entre em contato com a ong Pró-Carnívoros , especializada no manejo e conservação desses animais.
*Mariana Aprile é estudante de biologia na Universidade presbiteriana Mackenzie e bolsista de iniciação científica do Mackpesquisa (PIBICK).

MDC e MMC com exercícios

Máximo Divisor Comum - M.D.C.


Definimos Máximo Divisor Comum - M.D.C entre dois ou mais números como sendo o maior divisor comum entre eles.

Exemplo 1 : Consideremos, por exemplo, os números 18 e 30. Determinemos, inicialmente, o conjunto de seus divisores :

D(18) = { 1, 2, 3, 6, 9 e 18 } e D(30) = { 1, 2, 3, 5, 6, 10, 15 e 30 }

O Conjunto nos mostra os divisores comuns a 18 e 30 e dentre eles o maior, ou máximo,
será o 6 ; Com isso diremos que : M.D.C ( 18 e 30 ) = 6

Exemplo 2 : Consideremos, por exemplo, os números 24, 60 e 84. Determinemos, inicialmente, seus divisores :

D(24) = { 1, 2, 3, 4, 6, 8, 12 e 24 },
D(60) = { 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 e 60 } e
D(84) = { 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 e 84 }

O Conjunto nos mostra os divisores comuns a 24, 60 e 84 e dentre eles o maior, ou
máximo, será o 12 ; Com isso diremos que : M.D.C ( 18, 60 e 84 ) = 12

2.0 - Métodos para o Cálculo do M.D.C.


2.1 - 1º Método: Algoritmo de Euclides, Método das Divisões Sucessivas ou " Jogo da Velha "


Exemplo 1 : Calculemos, por exemplo, o M.D.C entre 48 e 72 .

Montemos um diagrama semelhante ao Jogo da Velha e nele colocaremos na ordem decrescente os números dados.

Passo 1 - Dividimos o maior 72 pelo menor 48, o quociente 1 dessa divisão colocaremos acima do divisor 48 e o resto da divisão 24
colocaremos abaixo do dividendo 72.

Passo 2 - Deslocamos o resto obtido 24 para o espaço a direita do divisor e Dividimos este 48 por ele 24, o quociente 2 dessa divisão
colocaremos acima do novo divisor e o resto da divisão 0 colocaremos abaixo do novo dividendo 48. Esse processo será repetido até
que chequemos ao resto zero.

Passo 3 - Quando o resto se tornar igual a zero concluímos que o último divisor será o M.D.C. procurado . Assim: M.D.C. ( 48 e 72 ) = 24



Exemplo 2 : Calculemos, por exemplo, o M.D.C entre 324 e 252 .

Montemos um diagrama semelhante ao Jogo da Velha e nele colocaremos na ordem decrescente os números dados.

Passo 1 - Dividimos o maior 324 pelo menor 252, o quociente 1 dessa divisão colocaremos acima do divisor 252 e o resto da divisão 72
colocaremos abaixo do dividendo 324.

Passo 2 - Deslocamos o resto obtido 72 para o espaço a direita do divisor e dividimos este 252 por ele 72, o quociente 3 dessa divisão
colocaremos acima do novo divisor 72 e o resto 36 colocaremos abaixo do novo dividendo 252.

Passo 3 - Deslocamos o resto obtido 36 para o espaço a direita do novo divisor 72 e dividimos este 72 por ele 36, o quociente 2 dessa
divisão colocaremos acima do divisor 36 e o resto da divisão 0 colocaremos abaixo do último dividendo 72.

Passo 4 - Como o resto se tornou igual a zero concluímos que o último divisor é o M.D.C. procurado . Assim M.D.C. ( 324 e 252 ) = 36



2.2 - 2º Método: Decomposição em Fatores Primos


Nesse método iremos decompor os números em fatores primos e aplicarmos a regra :

O M.D.C. entre dois ou mais números é dado pelo produto entre os fatores primos comuns, elevados aos menores expoentes

Exemplo 1 : Calculemos, por exemplo, o M.D.C entre 96 e 360.

Decompondo cada um dos números em fatores primos, teremos :

96 = 25 X 3 e 360 = 23 X 32 X 5. E aplicando a regra, teremos :

fatores comuns => 2 e 3 e elevados aos menores expoentes : 23 e 31. Com isso : M.D.C. ( 96 e 360 ) = 23 X 3 = 8 X 3 = 24

Exemplo 2 : Calculemos, por exemplo, o M.D.C entre 100, 180 e 840.

Decompondo cada um dos números em fatores primos, teremos :

100 = 22 X 52 180 = 22 X 32 X 5 e 840 = 23 X 3 X 5 X 7

E aplicando a regra, teremos :

fatores comuns => 2 e 5 e elevados aos menores expoentes : 22 e 51. Com isso : M.D.C. (100, 180 e 840) = 22 X 5 = 4 X 5 = 20

Exemplo 3 : Calculemos, por exemplo, o M.D.C entre A, B e C, sendo :

A = 22 X 35 X 54
B = 26 X 33 X 53 X 113 e
C = 24 X 34 X 52 X 75

Nesse caso os números já estão decompostos em fatores primos e aplicando a regra, teremos :

Fatores comuns => 2, 3 e 5 e elevados aos menores expoentes : 22, 33 e 52.

Com isso e deixando o resultado indicado como originalmente no exemplo : M.D.C. (A, B e C) = 22 X 33 X 52

3.0 - Características Marcantes do M.D.C.


5.04a - O M.D.C. entre dois ou mais números primos será sempre igual a unidade.

5.04b - O M.D.C. entre dois números consecutivos será sempre igual a unidade.

5.04c - O M.D.C. entre dois ou mais números pares será sempre igual a 2.

5.04d - Se A é múltiplo de B, o M.D.C. entre A e B será igual a B.

5.04e - Se B é divisor de A, o M.D.C. entre A e B será igual a B.

5.04f - Se multiplicarmos dois ou mais números por um número natural maior que zero, o M.D.C. entre eles também ficará multiplicado
por esse número.

5.04g - Se dividirmos dois ou mais números por um número natural maior que zero, o M.D.C. entre eles também ficará dividido por
esse número.

5.04h - Quando o M.D.C. entre dois números, não necessariamente primos, é 1, eles são chamados primos entre si.

4.0 - Mínimo Múltiplo Comum - M.M.C.


Definimos Mínimo Múltiplo Comum - M.M.C entre dois ou mais números como sendo o menor múltiplo comum não nulo entre eles.

Exemplo 1 : Consideremos, por exemplo, os números 12 e 18. Determinemos, inicialmente, o conjunto de seus múltiplos :

M(12) = { 0, 12, 24, 36, 48, 60, 72, … } e M(18) = { 0, 18, 36, 54, 72, 90, … }

O Conjunto nos mostra os múltiplos comuns a 12 e 18 e dentre eles o menor e
não nulo, ou mínimo, será o 36 ; Com isso, diremos que : M.M.C ( 12 e 18 ) = 36

Exemplo 2 : Consideremos, por exemplo, os números 6, 9 e 15. Determinemos, inicialmente, seus múltiplos :

M( 6 ) = { 0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, … } ,
M( 9 ) = { 0, 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, … } e
M( 15 ) = { 0, 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, … }

O Conjunto nos mostra os múltiplos comuns a 6, 9 e 15 e dentre eles o
menor e não nulo, ou mínimo, será o 90 ;

Com isso diremos que : M.M.C ( 6, 9 e 15 ) = 90

5.0 - Métodos para o Cálculo do Mínimo Múltiplo Comum - M.M.C.


5.1 - 1º Método para o Cálculo do M.M.C. : Decomposição em Fatores Primos


Nesse método iremos decompor os números em fatores primos e aplicarmos a regra :

O M.M.C. entre dois ou mais números é dado pelo produto entre todos os fatores primos, comuns e não comuns, elevados aos maiores
expoentes

Exemplo 1 : Calculemos, por exemplo, o M.M.C entre 24 e 50.

Decompondo cada um dos números em fatores primos, teremos : 24 = 23 X 31 e 50 = 21 X 52. E aplicando a regra, teremos :

todos os fatores => 2, 3 e 5 e elevados aos maiores expoentes : 23, 31 e 52. Com isso :

M.M.C. ( 24 e 50 ) = 23 X 31X 52 = 8 X 3 X 25 = 600

Exemplo 2 : Calculemos, por exemplo, o M.M.C entre A, B e C, sendo :

A = 22 X 35 X 5
B = 23 X 33 X 53 X 73
C = 24 X 34 X 52 X 74

Nesse caso os números já estão decompostos em fatores primos e aplicando a regra, teremos :

Todos os fatores => 2, 3, 5 e 7 e elevados aos maiores expoentes : 24, 35, 53 e 74. Com isso e deixando o resultado indicado como
originalmente no exemplo, teremos :

M.M.C. (A, B e C) = 24 X 35 X 53 X 74.

5.2 - 2º Método para o Cálculo do M.M.C. : Decomposição Simultânea.


Nesse método iremos decompor os números simultaneamente em fatores primos :

Exemplo 1 : Calculemos, por exemplo, o M.M.C entre 12 e 20.

Passo 1 - Coloquemos lado a lado os números e a direita deles tracemos uma linha vertical

Passo 2 - A partir daí dividiremos cada número pela sucessão dos números primos, enquanto pelo menos um deles for divisível a
operação deve ser continuada, e nesse caso repetiremos o número não divisível até que não seja mais possível também para o outro,
ou nenhum dos outros, a divisão.

Passo 3 - Quando cada coluna a esquerda apresentar a unidade, o produto de todos os fatores encontrados a direita nos dará o M.M.C. .



Com Isso o M.M.C. entre 12 e 20 será 22 X 3 X 5 = 60

Exemplo 2 : Calculemos, agora, o M.M.C entre 8, 14 e 20.



Com Isso o M.M.C. entre 8, 14 e 20 será 23 X 3 X 5 = 120

5.3 - 3º Método para o Cálculo do M.D.C. : Decomposição Simultânea.


Como já conhecemos como funciona o cálculo do M.M.C. pelo método da decomposição simultânea, podemos aplicá-lo também para
o cálculo do M.D.C.:

Exemplo 1 : Calculemos, por exemplo, o M.D.C entre 12 e 60 e 72.

Passo 1 - Faremos exatamente com se fossemos calcular o M.M.C. entre eles

Passo 2 - Quando cada coluna a esquerda apresentar a unidade, o produto de todos os fatores encontrados a direita do traço que
dividiram simultameamente todos os 3 números nos dará o M.D.C. entre eles.

12 , 60 , 72 2 <<<
6 , 30 , 36 2 <<<
3 , 15 , 18 2
3 , 15 , 9 3 <<<
1 , 5 , 3 3
1 , 5 , 1 5
1 , 1 , 1

Assinalamos com as 3 setinhas os fatores que dividiram ao mesmo tempo os 3 números. O produto desses números assinalados nos dará
o M.D.C. entre eles.

Com Isso o M.D.C entre 12 e 60 e 72 será 22 X 3 = 12

6.0 - Características Marcantes do M.M.C.


5.09a - O M.M.C. entre dois ou mais números primos será sempre igual ao produto entre eles.

5.09b - O M.M.C. entre dois números consecutivos será sempre igual ao produto entre eles.

5.09c - Se A é múltiplo de B, o M.M.C. entre A e B será igual a A.

5.09d - Se B é divisor de A, o M.M.C. entre A e B será igual a A.

5.09e - Se multiplicarmos dois ou mais números por um número natural maior que zero, o M.M.C. entre eles também ficará
multiplicado por esse número.

5.09f - Se dividirmos dois ou mais números por um número natural maior que zero, o M.D.C. entre eles também ficará dividido
por esse número.

7.0 - Propriedade Importante entre M.D.C. e M.M.C.


Dados dois números A e B, o produto entre seu M.D.C. e o seu M.M.C. , será igual ao produto A X B entre eles. Ou seja :

M.M.C. ( A e B ) x M.M.C.( A e B ) = A X B


Tente provar essa importante propriedade. É mais fácil que você imagina.

Importante: Essa propriedade somente é válida para o M.D.C. e o M.M.C. entre dois números

8.0 - Exercícios Propostos


I - Determine o M.D.C. entre :

01) dois números pares e consecutivos 02) dois números consecutivos
03) dois números ímpares e consecutivos 04) dois números primos
05) dois múltiplos pares e naturais de 9 06) 3 números terminados em 5
07) dois múltiplos inteiros de 7, positivos e consecutivos 08) dois múltiplos naturais cuja diferença é o triplo do menor


II - Determine pelo Algoritmo de Euclides ( Jogo da Velha ) o M.D.C. entre :

09) 24 e 60 10) 96 e 180 11) 132 e 198
12) 247 e 299 13) 624 e 720


14) Um aluno ao determinar o M.D.C. entre dois números pelo método das divisões sucessivas encontrou para M.D.C. 36 e
respectivamente os quocientes 1, 3 e 2. Cálculos esses dois números.

15) Um aluno ao determinar o M.D.C. de dois números pelo Algoritmo de Euclides encontrou 21 para M.D.C. e respectivamente
os quocientes 4, 2 e 2. Cálculos o maior desses números.

16) O M.D.C. de dois números determinado pelo Algoritmo de Euclides é 27. Se os 4 quocientes encontrados são distintos e os
menores possíveis, determi-ne o menor desses dois números.

17) Explique por que no cálculo do M.D.C. de dois números pelo Algoritmo de Euclides o último quociente encontrado é sempre
maior que a unidade.

III - Determine o M.D.C. entre :

18) 320 e 448 19) 462 e 1.386 20) 975 e 455
21) 28, 77 e 84 22) 108, 120 e 144 22) 60, 72, 96 e 156


IV - Qual é o maior número que divide exatamente :
23) 39, 65 e 143 24) 702 e 918 25) 519, 1.038 e 1.557


26) Qual é o maior número pelo qual devemos dividir 270 e 240 para obtermos, respectivamente, os restos 10 e 9 :

27) Qual é o maior número pelo qual devemos dividir 160, 220 e 472 para obtermos, respectivamente, os restos 7, 16 e 13

28) Ao dividirmos 167, 237, 379 e 593 pelo maior número possível, obtemos respectivamente os restos 23, 21,19 e 17.
Calcule esse número.

V - Encontrar dois números conhecendo-se sua soma S e seu M.D.C.. ( Obs : Dar todas as soluções possíveis )

29) Soma = 384 e M.D.C. = 24 30) Soma = 740 e M.D.C. = 37 31) Soma = 840 e M.D.C. = 56


VI - Encontrar dois números conhecendo-se sua soma D e seu M.D.C.. ( Obs : Dar todas as soluções possíveis )

32) Diferença = 75 e M.D.C. = 15 33) Diferença = 108 e M.D.C. = 18 34) Diferença = 378 e M.D.C. = 42


VII - Encontrar dois números conhecendo-se seu produto P e seu M.D.C.. ( Obs : Dar todas as soluções possíveis )

35) Produto = 1 536 e M.D.C. = 12 36) Produto = 1 792 e M.D.C. = 8 37) Produto = 4 320 e M.D.C. = 6


38) Encontrar três números distintos de 2 algarismos cujo M.D.C. é 13 e cuja soma é igual a 91.

VIII - Determine o M.MC. entre :

39) dois números pares e consecutivos 40) dois números consecutivos
41) dois números ímpares e consecutivos 42) dois números primos
43) dois múltiplos pares e naturais de 3 44) dois múltiplos naturais cuja diferença é o triplo do menor


IX - Determine o M.M.C. entre :

45) 32 e 48 46) 72 e 120 47) 26 e 65
48) 6, 7 e 210 49) 8, 12 e 14 50) 21, 28 e 36


X - Qual é o menor número simultaneamente divisível por :

51) 3, 4, 5, 6, 7 e 8 52) 2, 3 , 5, 8, 9 12 e 15 53) 11, 22, 33, 44 e 55
54) pelos 5 primeiros múltiplos positivos de 3 55) pelos números naturais menores que 11


XI - Determine o menor dos números que dividido por :

56) 12, 15 e 18 deixa o resto 8 57) 15, 24 e 30 deixa o resto 11
58) 24, 30, 36 e 60 deixa o resto 16 59) 32, 38 e 42 deixa o resto 17


XII - Encontrar dois números conhecendo-se sua soma S e seu M.M.C..

60) Soma = 30 e M.M.C. = 36 61) Soma = 140 e M.M.C. = 240 62) Soma = 168 e M.M.C. = 288


XIII - Encontrar dois números conhecendo-se sua soma P e seu M.M.C..

60) Produto = 360 e M.M.C. = 120 61) Produto = 2 160 e M.M.C. = 360 62) Produto = 1176 e M.M.C. = 108


63) Se o M.M.C. entre 70A e 56B é igual a 3 080. Determine os pares de valores possíveis para A e B.

XIV - Calcular o M.D.C. e o M.M.C. entre :

64) A = 23 x 34 x 5 e B = 22 x 32 x 52 65) P = 22 x 33 x 7 e Q = 2 x 34 x 5
66) M = 22 x 53 x 11 e N = 23 x 72 x 132 67) E = 23 x 3 x 5 x 72 , F = 22 x 33 x 52 x 112 e G = 2 X 32 X 73 X 112 X 17
68) A = 23 x 34 x 5 x 72 , B = 22 x 32 x 52 x 112 e C = 24 x 33 x 52 x 19 69) J = 23 x 34 x 5 x 72 , K = 22 x 32 x 52 x 112 e L = 24 x 33 x 52 x 19
70) M = 4 x 64 x 5 e P = 8 x 272 x 152


XV - Calcular o valor de n para as condições dadas :

71) A = 2n x 33 x 72 ; B= 24 x 32 x 7 x 112 para M.D.C. ( A e B ) = 23 X 32 X 7
72) Q = 22n x 32 x 52 ; B = 23 x 3n x 5 x 73 para M.M.C. ( A e B ) = 60
73) P = 24n x 9 ; B = 27 x 35 para M.D.C. ( A e B ) = 22 x 64
74) M = 30n X 7 ; B = 22 X 9 X 352 para M.M.C. ( A e B ) = 100 X 9 X 49


XVI - Calcular o valor de n + p para as condições dadas :

75) A = 2n X 33 X 132 ; B = 24 X 3p X 11 X 13 para M.D.C. ( A e B ) = 23 X 32 X 13
76) A = 2n X 32 X 11 ; B = 24 X 3p X 7 X 112 para M.M.C. ( A e B ) = 25 X 33 X 7 X 112


77) Calcular o valor da soma m + n + p tal que o M.D.C. entre A = 2m X 33 X 5p e B = 22 X 3n X 53 seja igual a 63 X 75

78) Dois números distintos A e B são os menores possíveis e podem ser representados, exclusivamente, pelos 3 menores fatores
primos. Se os expoentes do menor deles são números consecutivos. Determine o M.D.C. e o M.M.C. entre eles.

79) O produto de dois números A e B é igual a 360. Se o M.D.C. entre eles é 24, Calcule o seu M.M.C..

80) Uma doceria tem em estoque 150 balas de coco, 180 balas de chocolate e 240 balas de leite. Quantas balas de cada sabor se deve
colocar em caixas decoradas, sabendo que essas quantidades devem ser as maiores possíveis.

81) Três automóveis disputam uma corrida em uma pista circular. O mais rápido deles dá uma volta em 10 minutos, um outro leva
15 minutos e o terceiro e mais lento demora 18 minutos para dar uma volta completa. No fim de quanto tempo os 3 automóveis
voltarão a se encontrar no inicio da pista se eles partiram exatamente no mesmo instante.

82) Três automóveis disputam uma corrida em uma pista circular. Um deles dá uma volta em 18 minutos, um outro leva 20 minutos e o
terceiro demora 25 minutos para dar uma volta completa. Se eles partiram exatamente às 15 horas, Que horas serão quando os 3
automóveis voltarão a se encontrar no inicio da pista após 3 horas de corrida ?

83) Três netas visitam sua avó, respectivamente, em intervalos de 5 dias, de 7 dias e de 9 dias. Se a última vez em que as três se
encontraram na casa de sua avó foi no mês de Maio, em que mês do segundo semestre eles tornarão a se encontrar ?

84) Determine o menor número que ao ser dividido por por 11, 12 e 16 deixa, respectivamente, os restos 5, 6 e 10.

85) Determine o menor número de 4 algarismos que dividido por por 12, 15, 18 e 24 deixa, respectivamente, os restos 7, 10, 13 e 19.

9.0 - Questões de Concurso


86) ( CEFETQ - 1997 ) Determinar o maior número pelo qual se deve dividir os números 165 e 215 para que os restos sejam 9 e 11,
respectivamente.

87)( UFMG - 1996 ) O número de três algarismos divisível ao mesmo tempo por 2, 3, 5, 6, 9 e 11 é :

(A) 330 (B) 660 (C) 676 (D) 900 (E) 996


88) ( UNIFACS - 1997 ) O número de alunos de uma sala de aula é menor que 50. Formando-se equipes de 7 alunos, sobram 6.
Formando-se equipes de 9 alunos, sobram 6. Formando-se equipes de 9 alunos , sobram 5. Nessas condições, se forem formadas
equipes de 8 alunos, o número de alunos que sobram é :

(A) 1 (B) 2 (C) 3 (D) 4 (E) 5


89) ( PUC/CAMPINAS - 1995 ) Numa linha de produção, certo tipo de manutenção é feito na máquina A a cada 3 dias, na máquina B,
a cada 6 dias. Se no dia 2 de dezembro foi feita a manutenção das três máquinas, a próxima vez em que a manutenção ocorreu
no mesmo dia foi em :

(A) 5 de Dezembro (B) 6 de Dezembro (C) 8 de Dezembro (D) 14 de Dezembro (E) 26 de Dezembro


90) ( PUC/CAMPINAS - 1998 ) Uma editora tem em seu estoque 750 exemplares de um livro A, 1200 de um livro B e 2 500 de um livro C.
Deseja-se remetê-los a algumas escolas em pacotes, de modo que cada pacote os três tipos de livros em quantidades iguais e com o
maior número possível de exemplares de cada tipo. Nessas condições, remetidos todos os pacotes possíveis, o número de exemplares
que restarão no estoque é :

(A) 1.500 (B) 1.750 (C) 2.200 (D) 1.600 (E) 2.000

91) ( UNIARARAS - 1997 ) As cidade de Araras, Leme e Conchal realizam grandes festas periódicas, sendo as de Araras de 9 em
9 meses, as de Leme de 12 em 12 meses e as de Conchal de 20 em 20 meses. Se em Março de 1985 as festas coincidiram, então a
próxima coincidência foi em :

(A) Março de 1995 (B) Março de 2000 (C) Março de 1996 (D) Dezembro de 1999 (E) Nunca mais
www.matematicamuitofacil.com

Fatorial de um número

Professor Antonio Carlos Carneiro Barroso
http://ensinodematemtica.blogspot.com.br
extraido de www.colegioweb.com.br
Fatorial de um número:







Arranjo simples:

Interjeição

Classe invariável que expressa emoções, sensações...

Algumas expressões das interjeições: alívio (Ufa!); dor (Ai!); espanto (Quê!); medo (Credo!); satisfação (Viva!)...

Locução interjeitiva é o conjunto de duas ou mais palavras com valor de interjeição. Ex.: Que horror!; Queira Deus!

Uma palavra pertencente a outra classe pode transformar-se em interjeição, tudo depende do contexto e da expressividade com que é falada.
Ex.: Cuidado!; Coragem!
www.coladaweb.com

Congruências entre ângulos determinados por retas transversais

Reconhecer e compreender as relações e, principalmente, as congruências entre ângulos determinados por retas transversais em retas paralelas é importante para a resolução de problemas relacionados a triângulos, quadriláteros e outros polígonos - bem como os próprios problemas com ângulos.

Vejamos alguns conceitos fundamentais que vão ser úteis:

Ângulos opostos pelo vértice:

Na figura, os ângulos marcados com a mesma cor são opostos pelo vértice e possuem a mesma medida, ou seja, são congruentes.

<="" td="">

Ângulos suplementares:

São dois ângulos cuja soma vale 180º.

Na figura acima, sobre a mesma reta, temos um ângulo azul e um ângulo vermelho, cuja soma vale 180º, pois formam um ângulo raso.

Lembrados esses conceitos, vamos estudar as relações entre ângulos determinados por uma transversal em retas paralelas.

Observe a figura abaixo.

As retas r e s são paralelas "cortadas" pela transversal t.

Os ângulos 1, 2, 3 e 4 são os ângulos determinados pela transversal t em r - e os ângulos 5, 6, 7 e 8 são determinados por t em s.

Se "recortássemos" a figura conforme o pontilhado, poderíamos tranquilamente encaixar o pedaço recortado sobre a parte de baixo da figura, ou seja, os ângulos 1, 2, 3 e 4 "encaixariam" perfeitamente sobre os ângulos 5, 6, 7 e 8, nessa ordem:

<="" td="">

Assim, dizemos que esses ângulos são correspondentes e, como podemos perceber, ângulos correspondentes têm a mesma medida.

Como os pares 1 - 4 e 5 - 8 são opostos pelo vértice e 1 - 5 e 4 - 8 são correspondentes, todos eles têm a mesma medida.

Pelo mesmo motivo, 2, 3, 6 e 7 também têm a mesma medida.

Formando ângulo raso, temos 1 - 2, 3 - 4, 5 - 6, 7 - 8. Cada um desses pares forma um ângulo raso. Sabendo que 2, 3, 6 e 7 têm a mesma medida (ângulos obtusos) e que 1, 4, 5 e 8 têm a mesma medida (ângulos agudos), podemos observar na figura um ângulo agudo qualquer e um obtuso qualquer sendo sempre suplementares.

Nomeando as propriedades

Agora vamos nomear essas propriedades observadas. Para isso, é preciso entender um pouco a nomenclatura utilizada em geometria.

Dadas duas retas paralelas e uma transversal, os ângulos determinados pela transversal na região entre as paralelas são chamados de internos. Logo, os que não estão entre as paralelas são chamados de externos.

<="" td="">

Já os ângulos que estão do mesmo lado em relação à transversal, ou seja, do lado direito ou do lado esquerdo, são chamados colaterais. Os que estão em lados opostos são chamados alternos.

<="" td="">

<="" td="">

<="" td="">

<="" td="">

Voltando, então, à figura inicial, temos, em resumo:

<="" td="">

Alternos	Internos: 3 e 6, 4 e 5	São congruentes (mesma medida).
	Externos: 1 e 8, 2 e 7
Colaterais	Internos: 3 e 5, 4 e 6	Formam ângulo raso (medem juntos 180º).
	Externos: 1 e 7, 2 e 8
Correspondentes	1 e 5, 2 e 6, 3 e 7, 4 e 8	São congruentes.
Opostos pelo vértice	1 e 4, 5 e 8, 2 e 3, 6 e 7	São congruentes.

*Michele Viana Debus de França é licenciada em matemática pela USP e mestre em educação matemática pela PUC-SP.

Crase – Preposição “a” + artigo feminino “a”

valor de substantivo. Por esta razão, a crase não virá diante de verbos, nem tão pouco de pronomes pessoais (sujeito).
Contudo, tanto a preposição “a” quanto o artigo feminino “a” virão diante de substantivos femininos, já que os substantivos masculinos não admitem artigo feminino.
Observe:

Não irei à farmácia. Irei ao supermercado.

O verbo “ir” exige preposição, veja: Não irei. Onde? A algum lugar. Qual? A farmácia. Quem vai, vai a algum lugar. Na resposta “a qual lugar?” temos o artigo “a”. Logo, a preposição “a” mais o artigo feminino “a”, que acompanha o substantivo na resposta (a farmácia), formam a crase.

Agora, observe:

Não quero ler a capa deste livro.

O verbo “ler” ou a locução verbal “quero ler” não exigem preposição, portanto, o termo “a” que está na oração acima é um artigo feminino.

Declarei a ele que sou inocente.

Na oração acima, o pronome pessoal “ele” não admite artigo e, por isso, o termo “a” é uma preposição. Declarei algo a alguém. Quem? Ele (e não “a ele”).

• Preposição “a” e os pronomes demonstrativos

Os pronomes demonstrativos em que a crase pode ocorrer são: aquele, aquela, aqueles, aquelas, aquilo, a(s). Para isso, o termo regente deve exigir preposição. Por exemplo:

Assisti àquele programa horrível de TV.
Àquilo chamam de programa educativo?
Refiro-me àquela aluna estudiosa.

Sabrina Vilarinho
Graduada em Letras

Combinatória

Combinatória é a parte da matemática que se preocupa em agrupar e contar coleções de objetos, seguindo certos critérios de contagem.
Tais contagens podem ser feitas de duas maneiras: princípio aditivo e  princípio multiplicativo.

Princípio aditivo

O princípio aditivo ou  princípio da Inclusão-Exclusão é uma forma de contagem do número de elementos que pertencem à união de dois ou mais conjuntos não necessariamente disjuntos.
Para dois conjuntos A e B, o número de elementos dessa união é dado por:
n(A  B) = n(A) + n(B) – n(A  B)

Para três conjuntos A, B e C tem-se que o número da união é dado por:
n(A  B  C) = n(A) + n(B) + n(C) – n(A  B) – n(A  C) – n(B  C) + n(A  B  C).

Princípio multiplicativo

O princípio multiplicativo ou  princípio fundamental da contagem diz que se há x modos de se tomar uma decisão A e, tomada essa decisão há y modos de se tomar uma decisão B, então o número de modos de se pode tomar sucessivamente as decisões A e B é x . y.

Considerando x, y, z modos para, respectivamente, três decisões, tem-se x . y . z.

De uma forma geral, tendo-se x₁ maneiras de se tomar a decisão 1, x₂ maneiras de se tomar a decisão 2, . . . , x_n maneiras de se tomar a decisão n, então se terá ao todo:
x₁ . x₂ . . . x_n possibilidades.

Exemplo:
— Uma pessoa tem em seu guarda-roupa 3 calças, 6 blusas e 2 pares de sapatos, todos diferentes. De quantas maneiras distintas ela poderia se vestir usando uma peça de cada?

Como ela deve usar uma calça, uma blusa e um par de sapato, então o número total é dado por: 3 . 6 . 2 = 36.

Fatorial (!)

O fatorial de um número natural n, representado por n! (lê-se: “n fatorial ou fatorial de n”), é igual ao produto sucessivo desse número pelos seus antecessores até a unidade.
O fatorial de n é dado por:
n! = n.(n – 1).(n – 2).(n – 3). . .3.2.1
Assim, 5! = 5 . 4 . 3 . 2 . 1 = 120.

Por convenção, 0! = 1 e 1! = 1.

É fácil notar que 6! = 6 . 5 . 4 . 3 . 2 . 1 = 6 . 5! = 6 . 5. 4 . 3 . 2 . 1 = 6 . 5 . 4! = 6 . 5 . 4 . 3 . 2 . 1 = 6 . 5 . 4 . 3!
Então, se quando se está multiplicando pelos antecessores do número, parar antes do número 1, completa-se com o símbolo do fatorial.
Daí, o fatorial de n, pode ser escrito, por exemplo, como n! = n.(n – 1).(n – 2).(n – 3)! ou n! = n.(n – 1)!
Isto é muito útil para simplificar algumas expressões.

Exemplos:
 =  = 6 . 5 = 30.

 =  =  = 7 . 6 + 6 = 42 + 6 = 48.

Análise Combinatória

Permutações Simples

Dado um conjunto com n elementos no qual se deseja ordená-los, o número total de agrupamentos que pode ser feito é igual a:
n(n − 1)(n − 2) . . . 1, pois para a primeira posição pode-se ter n maneiras, para a segunda posição pode-se ter n − 1 maneiras; a terceira posição pode-se ter n − 2 maneiras, e assim sucessivamente até a última posição que só terá uma maneira de se escolher.
Portanto, o número de ordens em que se pode colocar n objetos distintos é n(n − 1)(n − 2) . . . 1 = n!

Chama-se permutação simples de n elementos distintos aos agrupamentos dos n elementos de modo que cada agrupamento difere do outro apenas pela ordem de seus elementos.
O número de permutação simples é dado por: P_n = n!

Exemplo:
— Com os dígitos 1, 2, 3 e 5, quantos números de quatro algarismos distintos podem ser formados?

Algarismos distintos quer dizer diferentes; qualquer exemplo que se faça tem exatamente 4 elementos e, por exemplo, 3215 e 3251 diferem apenas pela ordem dos elementos.
Logo, trata-se de uma permutação simples de 4 elementos (os números 1, 2, 3 ou 5) e, portanto:
P₄ = 4! = 4 . 3 . 2 . 1 = 24.

Arranjos Simples

Seja um conjunto com n elementos dos quais, se deseja formar agrupamentos de p elementos distintos, com p  n, onde cada agrupamento difere do outro pela natureza ou pela ordem de seus elementos.
Neste caso se tem um arranjo simples de n elementos tomados p a p.
O número de arranjos simples é dado por:  = A_{n, p} = 

Exemplo:
— Com os dígitos 1, 2, 3, 4, 5 e 6, quantos números de quatro algarismos distintos podem ser formados?

Qualquer exemplo usará apenas quatro dos seis elementos. Tanto 2345 é diferente de 2354 (pela ordem) como 2345 é diferente de 2346 (pela natureza dos elementos, pois, neste caso, não foram usados os mesmos elementos) e, portanto, trata-se de um arranjo simples (pois cada exemplo usa algarismos distintos) de 6 elementos tomados 4 a 4.
A_{6, 4} =  =  = 6 . 5 . 4 . 3 = 360. 

Combinação Simples

Seja um conjunto com n elementos dos quais, se deseja formar agrupamentos de p elementos distintos, com p  n, onde cada agrupamento difere do outro apenas pela natureza de seus elementos.
Neste caso se tem uma combinação simples de n elementos tomados p a p.
O número dessas combinações simples é dado por:  =  = C_{n, p} = 

Observações:

 =                   ex.:  =  = 

C_n,0 = C_n,n = 1 e   C_n,1 = n, qualquer que seja o natural n  1.

Exemplo:
— Quantos subconjuntos com 2 elementos possui um conjunto com 5 elementos?

Considerando os elementos a, b, c, d, f, um conjunto com dois seria, por exemplo, {a, b} e ele logicamente é diferente de, por exemplo, de {a, c}, pela natureza de seus elementos, mas os conjuntos {a, b} e {b, a} não são diferentes, mas sim o mesmo conjunto.
Então, trata-se de uma combinação simples de 5 elementos tomados 2 a 2.
C_{5, 2} =  =  =  = 20 / 2 = 10.

Permutação Circular ou Cíclica

Dado um conjunto com n elementos onde se deseja ordená-los de maneira que o primeiro e o último se encontrem, isto é, tenham a forma.

Neste caso se tem uma permutação circular que é diferente das permutações simples, pelo fato de que rodando os elementos não se tem outro agrupamento, pois, por exemplo, com os elementos A, B, C e D, em círculo, tem-se que ABCD, BCDA, CDAB e DABC são todos iguais e, portanto, correspondem a um único agrupamento.
O número de permutações cíclicas é dado por: PC_n = (n – 1)!

Exemplo:
— Quantas rodas de ciranda podem ser formadas com 5 crianças?

Como a primeira e a última estarão se encontrando em circulo tem-se uma permutação circular dos 5 elementos, isto é, PC₅ = (5 – 1)! = 4! = 24.

Permutação com Repetição

Supondo que se tem n elementos para permutar, sendo que q₁ desses elementos são de um mesmo tipo, q₂ de outro tipo, q₃ de outro tipo, e assim por diante, onde q₁ + q₂ + . . . + q_p n.
Neste caso se tem um permutação com repetição de n elementos onde se tem q₁ iguais a tipo, q₂ de outro tipo, . . .
O número de permutações com repetição é dado por:  = 

Exemplo:
— Quantos são os anagramas da palavra ARARAS?

Anagrama é a junção de letras tendo significado ou não (se fizer sentido é uma palavra), neste caso há seis elementos que serão permutados, porém 3 são de um mesmo tipo (letra A) e 2 de outro tipo (letra R), portanto tem-se uma permutação com repetição de 6 elementos com 3 e 2 tipos de repetições, logo há:  =  =  = 6 . 5 . 4 / 2 = 120 / 2 = 60.

Arranjo com Repetição

Seja um conjunto com n elementos e sendo p um número inteiro positivo menor ou igual a n, chama-se arranjo com repetição dos n elementos tomados p a p, a qualquer sequência de p elementos, onde pode haver repetições de elementos e sendo p o número máximo de repetições.
O número desses arranjos é dado por: AR_n,p = n^p (n elevado a p).

Exemplo:
Com os dígitos 1, 2, 4, 5, 7, e 9; quantos números de 3 algarismos podem ser formados?

Como não foi dito que os três algarismo devem ser distintos, então, por exemplo, 242 pode ser um desses números, e um número difere do outro tanto pela natureza com pela ordem de seus elementos, então se trata de um arranjo com repetição de 6 elementos 3 a 3.
AR_6,3 = 6³ = 6 . 6 . 6 = 216.

Combinação com Repetição

Seja um conjunto com n elementos dos quais, se deseja formar agrupamentos de p elementos não necessariamente distintos, onde cada agrupamento difere do outro apenas pela natureza de seus elemento, então se tem uma combinação com repetição de n elementos tomados p a p.
O número dessas combinações é dado por:  = CR_n,p =  = C_{n + p – 1,p}

Exemplo:
— Quantas são as soluções inteiras e não-negativas da equação x + y + z = 4?

De uma forma geral, pode-se considerar a equação como x₁ + x₂ + . . . + x_n = p.
Assim, n é o número de incógnitas e p o resultado da soma, então tem-se:
CR_3,4 = C_{3 + 4 – 1,4} = C_6,4 = C_6,2 =  =  = 6 . 5 / 2 = 30 / 2 = 15.

Se a questão fosse: quantas são as soluções inteiras positivas da equação x + y + z = 4?
Se tomaria x = a + 1, y = b + 1, z = c + 1, pois não poderia ter zero já que teria que ser positiva, daí a equação ficava:
a + 1 + b + 1 + c + 1 = 4 ou a + b + c = 4 – 3 ou a + b + c = 1, assim se teria n = 3 e p = 1, daí:
CR_3,1 = C_3+1–1,1 = C_3,1 = 3, que seriam {(1, 1, 2)}; (1, 2, 1); (2, 1, 1)}.

Observação:

A principal diferença entre arranjo e combinação é que no arranjo, os agrupamentos, por exemplo, ABC e ACB são diferentes, ou seja, a ordem importa e na combinação a ordem nãoimporta.
Assim, se em um grupo de 5 pessoas, 2 forem escolhidas para ir a igreja, falar dos escolhidos tanto faz dizer Ana e Bia como Bia e Ana.
Logo, trata-se de uma combinação.
Porém, se 2 forem escolhidos para presidente e vice, Ana e Bia (Ana é a presidente), já Bia e Ana (Bia é que é a presidente).
Logo, trata-se de um arranjo.

Exercícios Resolvidos

R01 — Quantos são os divisores de 2¹⁰ . 3⁹? Quantos divisores são pares?

Cada potência de 2 multiplicada por cada potência de 3 representa um divisor, assim 2⁰ . 3⁰= 1 . 1 = 1 é um divisor, 2¹ . 3⁰ = 2 . 1 = 2, outro, 2⁰ . 3¹ = 1 . 3 = 3 e, assim por diante, então os divisores dependem das potências, isto é, no caso do 2 os expoentes podem ser E(2) = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} e os de 3, E(3) = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
Então, há 11 possibilidades para a base 2 e 10 possibilidades para a base 3, então 11 . 10 = 110 divisores.

Para que o divisor seja para é necessário que o 2 não desapareça, isto é, que o expoente do 2 não seja zero, assim haverá 10 possibilidades para cada e, 10 . 10 = 100 divisores.

R02 — De quantas formas podemos pintar o quadro abaixo com as cores amarelo, preto e vermelho, sem que dois quadrados consecutivos tenham a mesma cor e que nem o primeiro nem o último sejam pintados de amarelo?
 

Começa-se pelas condições impostas que é para o primeiro e o sexto há apenas duas opções (vermelho ou preto), a segunda posição pode-se pintar com qualquer uma das três cores exceto a que foi pintada a primeira, para terceira e quarta a mesma coisa, porém na quinta posição não se poder pintar com a mesma cor da quarta nem da sexta, então só há uma opção.
Assim tem-se: 2 . 2 . 2 . 2 . 1 . 2 = 32 modos diferentes.

R03 — Quantos são os anagramas da palavra “PRATO” que começam por consoante?

Cada anagrama corresponde a uma ordem das 5 letras. Para formar um anagrama começando por consoante se deve começar por P, R ou T.
Se começar por P significa que ele não irá trocar de lugar com as demais, P __ __ __ __ e apenas quatro elementos irão permutar.
O mesmo ocorre, com o fato de se começar por R __ __ __ __ ou T __ __ __ __, totalizando “três casos” iguais, logo se tem:
P₄ + P₄ + P₄ = 3 . P₄ = 3 . 4! = 3 . 24 = 72.

R04 — De quantas formas pode-se ordenar 8 pessoas de modo que duas determinadas pessoas não fiquem juntas?

O número total que se pode ordenar é dado pela permutação de todos os oito elementos P₈, mas isto inclui os casos em que duas determinadas estejam juntas.
Supondo que Ana e Bia, por exemplo, sempre ficassem juntas, elas formariam apenas um elemento ficando as duas mais seis, totalizando então sete: P₇, mas as duas também poderiam permutar entre si, neste caso, permutação das duas: P₂.
O número que as duas ficariam juntas é P₇ . P₂.
Então, para que duas não fiquem juntas tem-se o número total menos os casos em que estão juntas. Logo, se tem:
P₈ – P₂ . P₇ = 8! – 2! . 7! = 8 . 7! – 2 . 7! = 7!(8 – 2) = 6 . 7! = 6 . 7 . 6! = 42 . 720 = 30 240.

R05 — De quantas formas podemos acomodar 3 pessoas em 5 cadeiras?

Neste caso, tem-se cinco cadeiras: A, B, C, D, E das quais se usará apenas 3 (onde sentarão as três pessoas).
Claro que a escolha ABC é diferente de ABD, pois são cadeiras diferentes.
ABC e ACB embora sejam as mesmas cadeiras são agrupamentos diferentes, pois as pessoas são distintas e sentando em posições diferentes formam outro agrupamento.
Logo, tem-se um arranjo simples de 5 elementos tomados 3 a 3.
A_5,3 =  =  = 5 . 4 . 3 = 60.

R06 — Numa reta há 6 pontos e em outra reta paralela a esta, 5 pontos. Quantos triângulos podem ser formados com esses pontos? E quantos quadriláteros?

Como as retas são paralelas, pegando dois pontos de uma reta e um ponto da outra reta forma-se um triângulo, e como, por exemplo, os vértices A e B da primeira reta forma com o vértice C da segunda reta um triângulo e o vértice C da segunda reta forma com os vértices A e B da primeira reta o mesmo triângulo. Logo, trata-se de uma combinação simples onde se escolhe 2 pontos na primeira reta e 1 na segunda reta (como é 'e' então multiplica-se) ou(como é 'ou' soma-se) 1 ponto na primeira reta e 2 pontos na segunda reta.
Daí, C_6,2 . C_5,1 + C_6,1 . C_5,2 =  . 5 + 6 .  = 15 . 5 + 6 . 10 = 75 + 60 = 135.

Para formar quadriláteros, é preciso escolher 2 pontos em cada reta e portanto, C_6,2 . C_5,2 = .  = 15 . 10 = 150.

R07 — Quantos são os anagramas da palavra ANAGRAMA, que mantêm juntas as letras ANGM nesta ordem? E que tenham as letras NGRM juntas?

Como as letras ANMG devem ficar juntas elas formam apenas um elemento que com as letras AAAN restantes, formam 5 elementos que serão permutadas, mas há repetição da letra A (3 vezes, já que a letra A que está formando um elemento em ANMG não está sozinha).
Logo, trata-se de uma permutação com repetição de 5 elementos com 3 repetidos.
PR_5,3 =  =  = 5 . 4 = 20.

Considerando que as letras NMGR, podem ser permutadas entre si, tem-se P₄ maneiras e, como elas formam um elemento que junto das demais AAAA, formam 5 elementos com repetição das quatro letras A, tem-se PR_5,4 maneiras.
Como acontece uma coisa e outra, tem-se, portanto o produto dos dois, isto é:
P₄ . PR_5,4 = 4! .  = 5! = 120.

R08 — Seja A um conjunto com 4 elementos e outro B, com 3 elementos. Quantas são as funções de A em B? E quantas são sobrejetoras?

Para ser função, nenhum elemento do primeiro conjunto pode sobrar, contudo eles podem ter o mesmo correspondente e portanto, no máximo quatro repetições e daí, AR_3,4 = 3⁴ = 3 . 3 . 3 . 3 = 81.

Supondo A = {1, 2, 3, 4} e B = {6, 7, 8} tais conjuntos e como para ser sobrejetora, não pode sobrar elementos no segundo conjunto tem-se que do total de funções deve-se retirar aquelas que não se correspondem com os 3 elementos de B, ou seja, aquelas que se correspondem apenas com 1 ou com 2 elementos.
Para que todos os elementos do conjunto A se correspondam com 2 de B, tem-se C_3,2 (para a escolha dos dois dentre os 3) e um dos dois seria repetido no máximo 4 vezes, daí AR_2,4, mas nesse caso conta-se duas vezes {(1, 6); (2, 6); (3, 6); (4, 6)}, {(1, 7); (2, 7); (3, 7); (4, 7)} e {(1, 8); (2, 8); (3, 8); (4, 8)}, quando se escolheu dso três elementos de o {6,7}, {7, 8} e {6, 8}. Para que todos os elementos do conjunto A se correspondam com 1 de B, tem-se C_3,1(para escolher um dos três) e este seria repetido no máximo 4 vezes, daí AR_1,4.
Assim, C_3,2 . AR_2,4 – C_3,1 . AR_1,4 = 3 . 2⁴ – 3 . 1⁴ = 3 . 16 – 3 . 1 = 48 – 3 = 45.
Então, o número de funções sobrejetoras é 81 – 45 = 36.

De uma forma geral se n(A) = m e n(B) = n o número de funções sobrejetoras de A em B é dado por:
 . C_{n,n – p} . (n – p)^m.

R09 — Num parque há 5 tipos de brinquedos que podem usar o mesmo bilhete de entrada. Com 3 bilhetes de quantas formas se pode brincar neste parque usando todos os bilhetes?

Sendo os brinquedos A, B, C, D, E, se os bilhetes forem utilizados na forma ABC ou BAC dá no mesmo, pois são os mesmos brinquedos. Então, trata-se de uma combinação, mas pode-se brincar no mesmo brinquedo até 3 vezes, logo é com repetição.
Portanto, uma combinação com repetição de 5 tomados 3 a 3.
CR_5,3 = C_{5 + 3 – 1,3} = C_7,3 = 7! / 3! . (7–3)! = 7 . 6 . 5 . 4! / 3! . 4! = 7 . 6 . 5 / 3 . 2 . 1 = 35.

R10 — Para jogar dominó em uma mesa retangular é preciso 4 pessoas. Tendo de pessoas, de quantas maneiras pode-se realizar esse jogo?

Para escolher as quatro pessoas que irão jogar tem-se uma combinação de 6 tomados 4 a 4 (pois na escolha tanto faz ABCD com ACBD) e para os quatro que irão jogar tem-se uma permutação circular destes.
Como C_6,4 = C_6,2, tem-se:
C_6,2 . PC₄ =  . (4 – 1)! = 6 . 5 / 2 . 3! = 15 . 6 = 90.

R11 — Sabendo-se que C_8,p+2 / C_8,p+1 = 2, determine o valor de p.

Como – (p + 2) = – p – 2 e – (p + 1) = – p – 1, tem-se:

 /  =  .  =  . =  = 2, e dai tem-se:

7 – p = 2.(p + 2)        7 – p = 2p + 4         7 – 4 = 2p + p        3 = 3p    e, portanto, p = 1.

R12 — Quantos coquetéis (mistura de duas ou mais bebidas) podem ser feitos a partir de 7 ingredientes distintos?

Como é para se formar os coquetéis com pelo menos dois ingredientes, tem-se com 2, 3, 4, 5, 6 ou 7 vitaminas diferentes, ou seja,
 +  +  +  +  +  = 7 . 6 / 2! + 7 . 6 . 5 / 3! + 7 . 6 . 5 / 3! + 7 . 6 / 2! + 7 + 1 = 21 + 35 + 35 + 21 + 7 + 1 = 120.

Observações:
 =                     =                     =  = 7                    =  = 1

Exercícios Propostos

P01 — Quantos divisores de 2¹⁰ . 3⁹ formam quadrados perfeitos?

P02 — Em uma sala há 6 lâmpadas com seis interruptores distintos. De quantos modos pode ser iluminada essa sala?

P03 — De quantas maneiras pode-se dispor 4 homens e 4 mulheres em uma fila, sem que dois homens fiquem juntos?

P04 — Lançam-se três dados. Em quantos dos resultados possíveis, a soma dos pontos é 12?

P05 — Quantos inteiros entre 1000 e 10000 inclusive, não são divisíveis por 2 nem por 5?

P06 — De quantas formas pode-se ter o 1^o, 2^o e 3^o lugares de um campeonato com 10 times?

P07 — Com as letras da palavra ADEUS, se pode formar:
a) quantos anagramas?
b) quantos anagramas que começam com a letra D?
c) quantos anagramas que começam com vogal?
d) quantos anagramas que começam com consoante e terminam em vogal?

P08 — De quantos modos pode-se ordenar 2 livros de matemática, 3 de português e 4 de física, de modo que os livros de uma mesma matéria fiquem sempre juntos e, além disso, os de física fiquem sempre na mesma ordem?

P09 — Quantos são os anagramas da palavra INDEPENDENTE:
a) começados por IND?
b) começados por IND e terminados em T?
c) que contenham as letras I e P sempre juntas?
d) que contenham as letras I e P sempre juntas nesta ordem?
e) que contenham as letras I e P sempre juntas e termine em TE?

P10 — Com os dígitos 1, 2, 3, 4 e 5, quantos números de 5 algarismos distintos e maiores que 30 000 se pode formar?

P11 — Quantos números pares de três algarismos distintos pode-se formar com os dígitos 1, 3, 5, 6, 8 e 9?

P12 — Quantos números ímpares, compreendidos entre 300 e 4 000 e com todos os algarismos distintos, pode-se formar com os dígitos 1, 3, 5, 6, 7 e 9?

P13 — Quantas matrizes quadradas de ordem 3 pode-se formar usando os dígitos 1, 2 e 3, cada um uma vez e seis zeros?

P14 — Um trem é constituído de 1 locomotiva e 6 vagões distintos, sendo um deles restaurante. Sabendo que a locomotiva deve ir à frente e que o vagão-restaurante não pode ser colocado imediatamente após a locomotiva, encontre o número de modos diferentes para montar a composição?

P15 — Quantos números de 3 algarismos distintos pode-se formar com os 10 primeiros números naturais?

P16 — De quantas maneiras pode-se escolher 3 representantes de um grupo de 10 pessoas?

P17 — Uma empresa tem 3 diretores e 5 gerentes. Quantas comissões de 5 pessoas podem se formadas contendo no mínimo 1 diretor?

P18 — Uma sociedade tem um conselho administrativo formado por 12 membros, sendo 3/4 de brasileiros e os demais estrangeiros. Quantas comissões de 5 conselheiros podem ser formadas com 3 brasileiros?

P19 — De quantas maneiras distintas um grupo de 10 pessoas pode ser divididos em 3 grupos de 5, 3 e 2 pessoas?

P20 — Com os dígitos 0, 1, 2, 3, 4, 5 e 6 são formados números de 4 algarismos distintos. Quantos são divisíveis por 5?

P21 — Com os dígitos 0, 1, 2, 3, 4, 5 e 6 são formados números de 4 algarismos. Quantos são divisíveis por 5?

P22 — Qual o número de diagonais do decágono?

P23 — Calcular o número de múltiplos de 9 com 4 algarismos distintos que podem ser formados com os dígitos 2, 3, 4, 6 e 9?

P24 — Considerando que a loteria esportiva tenha 13 jogos, quantos são os possíveis resultados?

P25 — Sabendo que as placas de carro são formadas por 3 letras e 4 números, qual o número máximo de carros que podem ser emplacados em uma cidade onde só pode começar por K ou L?

P26 — Colocando em ordem crescente todos os números de 5 algarismos distintos obtidos com 1, 3, 4, 6 e 7, que posição ocupa o número 61 473?

P27 — Quantos são os naturais ímpares com 5 algarismos distintos?

P28 — Quantos são os anagramas da palavra ESTUDAR que começam com vogal? Que começam e terminam em vogal? Que tenham as vogais juntas?

P29 — De quantas maneiras pode-se ordenar 5 livros de Matemática, 3 livros de Química e 2 livros de Física, todos diferentes, de forma que os livros de uma mesma disciplina fiquem juntos?

P30 — De quantas formas pode-se ordenar 6 moças e 4 rapazes de modo que as moças permaneçam juntas?

P31 — De quantas formas pode-se ordenar 8 pessoas de modo que duas determinadas pessoas não fiquem juntas?

P32 — Quantos são os anagramas da palavra MATEMÁTICA de forma que as vogais e as consoantes sempre fiquem alternadas?

P33 — Quantos são os anagramas da palavra ÁLGEBRA que não possuem 2 vogais juntas?

P34 — De quantas formas podemos pintar o quadro abaixo com as cores: verde, amarelo, azul e branco, sem que dois quadrados consecutivos tenham a mesma cor?

P35 — Quantas são as raízes inteiras não negativas da equação x + y + z = 6?

P36 — Quantas são as raízes inteiras positivas da equação x + y + z = 7?

P37 — Quantos subconjuntos com 3 elementos possui um conjunto com n elementos?

P38 — Quantos são os anagramas da palavra COMBINATÓRIA? Que alternam consoantes e vogais? Que possuem as vogais juntas?

P39 — Quantos segmentos de reta podem ser formados com extremidades em 15 pontos dados?

P40 — Quantas diagonais possui um polígono convexo com 8 lados?

P41 — De quantas maneiras podemos pedir um sorvete de três bolas se dispomos de 5 sabores diferentes?

P42 — Quantos são os anagramas da palavra ESCOLA que terminam em vogal?

P43 — Quantos são os números com 5 algarismos não repetidos formados com 1, 2, 3, 4, 5? E que sejam ímpares? E que sejam maiores que 34 125?

P44 — Quantos são os números com 10 algarismos? E se os algarismos forem distintos?

P45 — De quantas maneiras podemos arrumar 9 pessoas em 3 quartos cada quarto com 3 pessoas?

fonte:hpdemat.apphb.com