Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Integrais
Integrais indefinidas
Da mesma forma que a adição e a subtração, a multiplicação e a divisão, a operação inversa da derivação é a antiderivação ou integração indefinida.
Dada uma função g(x), qualquer função f'(x) tal que f'(x) = g(x) é chamada integral indefinida ou antiderivada de f(x).
Exemplos:
- Se f(x) =
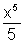, então 
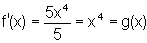é a derivada de f(x). Uma das antiderivadas de f'(x) = g(x) = x4 é .
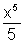- Se f(x) = x3, então f'(x) = 3x2 = g(x). Uma das antiderivadas ou integrais indefinidas de g(x) = 3x2 é f(x) = x3.
- Se f(x) = x3 + 4, então f'(x) = 3x2 = g(x). Uma das antiderivadas ou integrais indefinidas de g(x) = 3x2 é f(x) = x3 + 4.
Nos exemplos 2 e 3 podemos observar que tanto x3 quando x3+4 são integrais indefinidas para 3x2. A diferença entre quaisquer destas funções (chamadas funções primitivas) é sempre uma constante, ou seja, a integral indefinida de 3x2 é x3+C, onde C é uma constante real.
Propriedades das integrais indefinidas
São imediatas as seguintes propriedades:
1ª.
, ou seja, a integral da soma ou diferença é a soma ou diferença das integrais.2ª.
, ou seja, a constante multiplicativa pode ser retirada do integrando.3ª.
, ou seja, a derivada da integral de uma função é a própria função.Integração por substituição
Seja expressão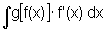 
.
.
Através da substituição u=f(x) por u' = f'(x) ou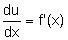 
, ou ainda, du = f'(x) dx, vem:
, ou ainda, du = f'(x) dx, vem:
,
admitindo que se conhece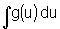 
.
.
O método da substituição de variável exige a identificação de u e u' ou u e du na integral dada.
INTEGRAIS DEFINIDAS
INTEGRAIS DEFINIDAS
Seja uma função f(x) definida e contínua num intervalo real [a, b]. A integral definida de f(x), de a até b, é um número real, e é indicada pelo símbolo:
 |
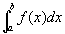onde:
- a é o limite inferior de integração;
- b é o limite superior de integração;
- f(x) é o integrando.
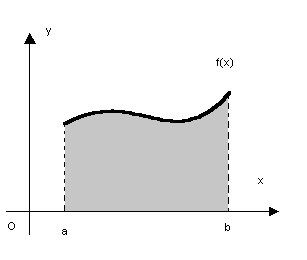
Se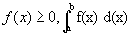 
representa a área entre o eixo x e a curva f(x), para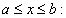 
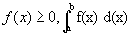representa a área entre o eixo x e a curva f(x), para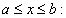 
 |
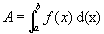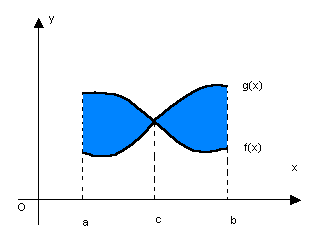
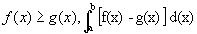representa a área entre as curvas, para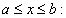 
 |
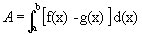Integrais
 |
 |
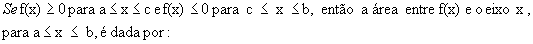
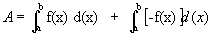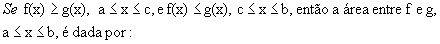
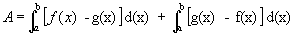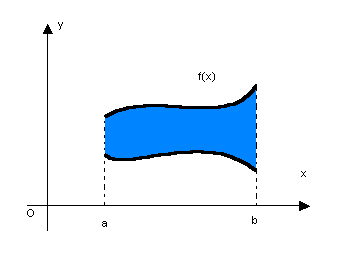
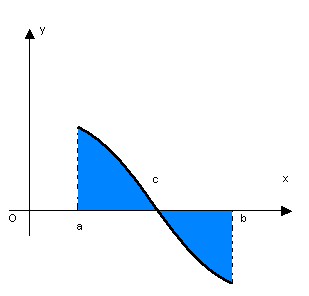
A integral definida, nos exemplos vistos, representa uma área, o que ocorre em muitos casos, e é uma das formas de se apresentar a integral definida.
De forma geral, para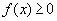 
, a área limitada por f(x) e o eixo x, 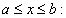é dada por 
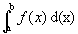, que pode representar a soma das áreas de infinitos retângulos de largura 
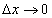e cuja altura é o valor da função num ponto do intervalo da base:
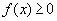, a área limitada por f(x) e o eixo x, 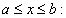é dada por 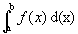, que pode representar a soma das áreas de infinitos retângulos de largura 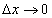e cuja altura é o valor da função num ponto do intervalo da base: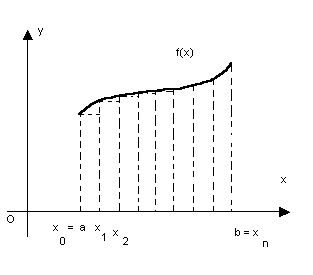
Subdividindo o intervalo [a, b] em n subintervalos através das abscissas x0=a, x1, x2,...,xn=b, obtemos os intervalos (a, x1), (x1, x2), ...., (xn-1, b). Em cada intervalo (xi-1, xi) tomemos um ponto arbitrário hi.
Seja
De acordo com a figura, os retângulos formados têm área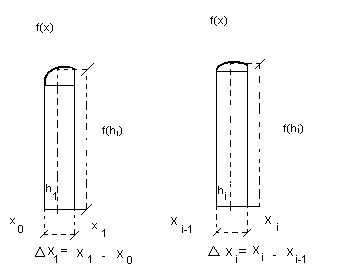 
Então, a soma da áreas de todos os retângulos é:
que nos fornece um valor aproximado da área considerada.
Aumentando o número n de subintervalos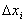 
, tal que 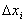tenda a zero 
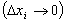e o número n de subintervalos tenda a infinito 
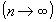, temos as bases superiores dos retângulos e a curva praticamente se confundindo e, portanto, temos a área considerada.
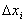, tal que 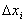tenda a zero 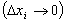e o número n de subintervalos tenda a infinito 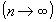, temos as bases superiores dos retângulos e a curva praticamente se confundindo e, portanto, temos a área considerada.
Simbolicamente, escrevemos:
 |
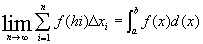Exemplo:
Seja a área entre y = x e o eixo x, para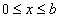 
:
:
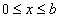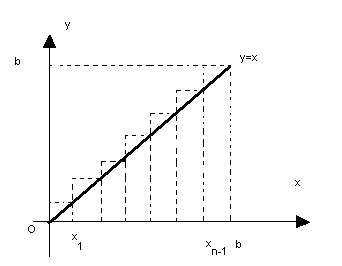
Esta área é dada por:
Podemos notar que o processo do limite nos leva ao resultado procurado. Dividindo o intervalo [0, b] em n subintervalos, cada um terá largura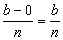 
.
.
Sejam, então, os pontos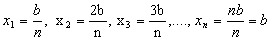 
.
.
Como f(x) = x, então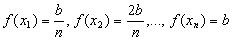 
.
.
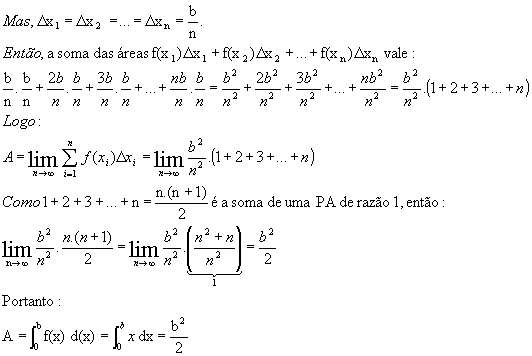
CÁLCULO DA INTEGRAL DEFINIDA
O método que temos para o cálculo da área ou da integral definida, no caso, é ainda muito complicado, conforme vimos no exemplo anterior, pois encontraremos somas bem piores.
Para tal, consideremos a área das figuras quando movemos a extremidade direita:
 |  |
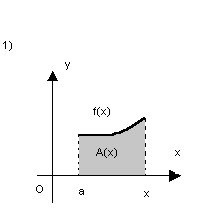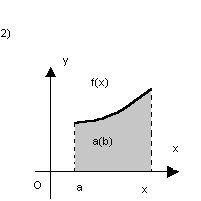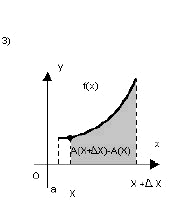
Se a área é dada por A(x), então A(a) = 0, pois não há área alguma. Já A(x) dá a área da figura 1, A(b), a área entre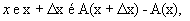 
ou seja:
ou seja:
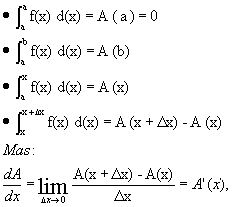
ou seja, A(x) é uma das antiderivadas de f(x). Mas sabemos que se F(x) é antiderivada qualquer de f(x), então A(x) = F(x) + C. Fazendo x = a, temos: A(a) = F(a) + C = 0 (A(a) = 0)
Logo, C = - F(a) e A(x) = F(x) - F(a).
Portanto:
 |
ou ainda,
 |
Exemplos:
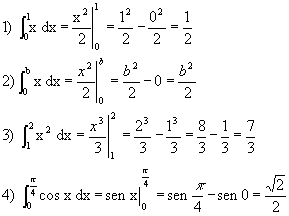
Note que conseguimos uma forma de calcular integrais definidas e áreas sem calcular somas complicadas e usando apenas as antiderivadas.
PROPRIEDADES DA INTEGRAL DEFINIDA
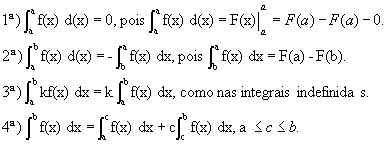
www.somatematica.com.br
a
ResponderExcluir