Colégio Estadual Dinah Gonçalves
email
accbarroso@hotmail.com
Quadrilátero
Quadrilátero é um polígono de quatro lados.
|
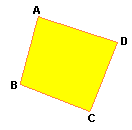 Quadrilátero ABCD |
Em um quadrilátero, dois lados ou dois ângulos não-consecutivos são chamados opostos.
|
Elementos
Na figura abaixo, temos:
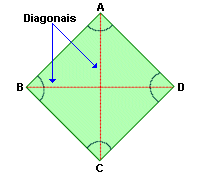 Quadrilátero ABCD |
Vértices: A, B, C, e D.
Lados: Diagonais:
Ângulos internos ou ângulos do
quadrilátero ABCD: |
Observações
- Todo quadrilátero tem duas diagonais.
- O perímetro de um quadrilátero ABCD é a soma das medidas de seus lados, ou seja: AB + BC + CD + DA.
Côncavos e Convexos
Os quadriláteros podem ser convexos ou côncavos.
Um quadrilátero é convexo quando a reta que une dois vértices consecutivos não encontra o lado formado pelos dois outros vértices.
Um quadrilátero é convexo quando a reta que une dois vértices consecutivos não encontra o lado formado pelos dois outros vértices.
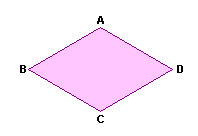 Quadrilátero convexo | 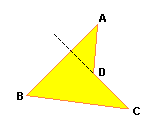 Quadrilátero côncavo |
Quadrilátero
Soma das medidas dos ângulos internos de um quadrilátero convexo
A soma do ângulos internos de um quadrilátero convexo é 360º.
|
Podemos provar tal afirmação decompondo o quadrilátero ABCD nos triângulos ABD e BCD.
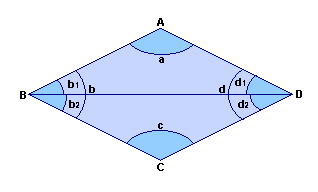
a + b1 + d1 = 180º. 1
Do triângulo BCD, temos:
c + b2 + d2 = 180º. 2
Adicionando 1 com 2 , obtemos:
a + b1 + d1 + c + b2 + d2 = 180º + 180º
a + b1 + d1 + c + b2 + d2 = 360º
a + b + c + d = 360º
Observações
1.Termos uma fórmula geral para determinação da soma dos ângulos internos de qualquer polígono convexo:
Si = (n - 2)·180º, onde n é o número de lados do polígono.
|
2. A soma dos ângulos externos de um polígono convexo qualquer é 360º.
Se = 360º
|
Quadriláteros Notáveis
Paralelogramo
Paralelogramo é o quadrilátero que tem os lados opostos paralelos.
|
Exemplo:
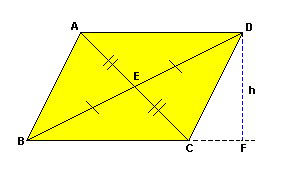 | 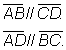 h é a altura do paralelogramo. |
| O ponto de intersecção das diagonais (E) é chamado centro de simetria. Destacamos alguns paralelogramos: | |
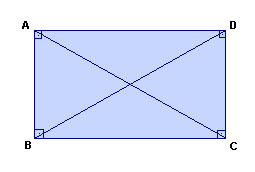
Retângulo é o paralelogramo em que os quatro ângulos são congruentes (retos).
|
Exemplo:
 |  |
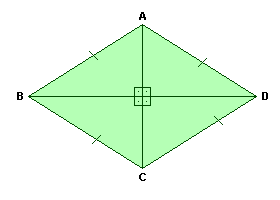
Losango é o paralelogramo em que os quatro lados são congruentes.
|
Exemplo:
 |  |
Quadrado é o paralelogramo em que os quatro lados e os quatro ângulos são congruentes.
|
Exemplo:
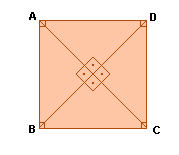
É o único quadrilátero regular. É, simultaneamente retângulo e losango.
| 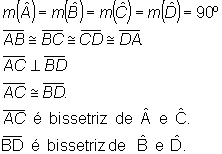 |
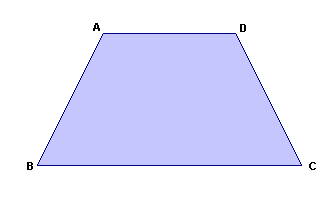
Trapézio
| É o quadrilátero que apresenta somente dois lados paralelos chamados bases. |
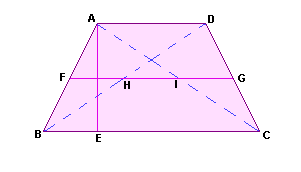


Denominamos trapezóide o quadrilátero que não apresenta lados paralelos.
Destacamos alguns trapézios:
Trapézio retângulo
É aquele que apresenta dois ângulos retos.
|
Exemplo:
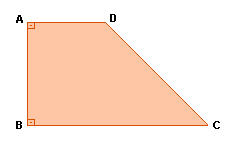 | 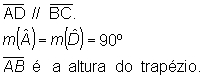 |
É aquele em que os lados não-paralelos são congruentes.
|
Exemplo:
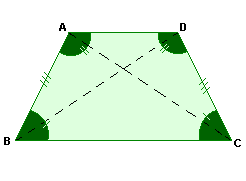

Trapézio escaleno
É aquele em que os lados não-paralelos não são congruentes.
|
Exemplo:
 |
Propriedades dos Paralelogramos
1ª Propriedade
Os lados opostos de um paralelogramo são congruentes.
|
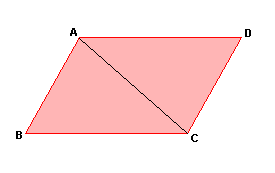 | H: ABCD é paralelogramo. T: |
| Demonstração | |
| Afirmativa | Justificativa |
| Segmentos de paralelas entre paralelas. | |
| Segmentos de paralelas entre paralelas. |
Cada diagonal do paralelogramo o divide em dois triângulos congruentes.
|
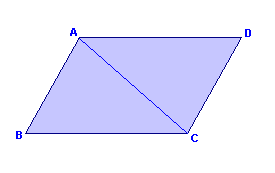 | H: ABCD é paralelogramo. T: |
| Demonstração | |
| Afirmativa | Justificativa |
| Hipótese. | |
| Hipótese. | |
| Lado comum. | |
| Caso L.L.L. |
As diagonais de um paralelogramo interceptam-se mutuamente ao meio.
|
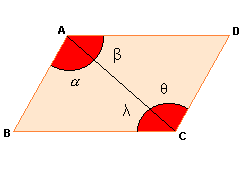 | H: ABCD é paralelogramo T: |
| Demonstração | |
| Afirmativa | Justificativa |
| Ângulos correspondentes em triângulos congruentes. | |
| Ângulos correspondentes em triângulos congruentes. | |
4ª Propriedade
As diagonais de um paralelogramo interceptam-se mutuamente ao meio.
|
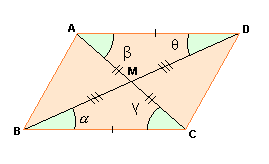 | H: ABCD é paralelogramo. T: |
| Demonstração | |
| Afirmativa | Justificativa |
| Ângulos alternos internos. | |
| Lados opostos (1ª propriedade). | |
| Ângulos alternos internos. | |
| Caso A.L.A.. | |
| Lados correspondentes em triângulos congruentes. |
Num paralelogramo:
- os lados opostos são congruentes;
- cada diagonal o divide em dois triângulos congruentes;
- os ângulos opostos são congruentes;
- as diagonais interceptam-se em seu ponto médio.
| As diagonais de um retângulo são congruentes. |
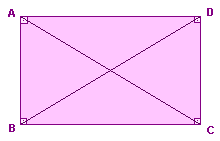 | T: ABCD é retângulo. H: |
Me ajuda a fazer por favor :)
ResponderExcluirPA
1- Calcule o X na sequencia (2x+1, 2x+4, x+2)
2- Calcule o 34° termo da PA (5, 7, 9)
3- Calcule o 1° termo de uma PA onde a21=60 e R=3
4- Calcule a razão de uma PA onde a16=36 e a1=2
PG
1- Calcule o 10= termo de PG (4, 8, 16...)
2- Calcule o próximo numero da sequencia (5, 15...)
3- Defina PG
ta dificil
ResponderExcluir