sexta-feira, 3 de setembro de 2021

Radical duplo na soma de dois simples.

Na obra de Sebastião e Silva incluem-se livros escolares do liceu: de Matemática “clássica”, os Compêndios de Álgebra para o 6.º e 7.º anos (em colaboração com J. da Silva Paulo),  Geometria Analítica,  para o 7.º ano; de Matemática “moderna”,  o Compêndio de Matemática I, II e III e respectivos Guias (Texto-piloto segundo o projecto executado pelo Ministério da Educação Nacional em cooperação com a O.C.D.E.).
Estes últimos serviram para apoiar os professores e alunos das turmas piloto que seguiram, em finais de 1960 e princípios de 1970,  um programa inovador, por ele concebido, considerado de nível internacional.
Eu segui o programa antigo e só contactei com o primeiro livro de Sebastião e Silva de Matemática “moderna”, já no início do meu primeiro ano do Técnico, para aprender melhor uma breve introdução à Lógica que iniciava as Matemáticas Gerais, em 68/69, do Prof. Campos Ferreira, um dos seus seguidores.
Sempre achei a exposição dos seus livros excelente e, ao mesmo tempo, cativadora e rigorosa. Foi à Álgebra do meu 7.º ano (pp.141-144) que recorri para relembrar uma transformação de um radical duplo na soma de dois simples, que é enunciada sob a forma do seguinte problema:
« Dados dois números racionais positivos A e B, não sendo B um quadrado perfeito, determinar dois números racionais positivos x e y tais que
\sqrt{A\pm\sqrt{B}}=\sqrt{x}\pm\sqrt{y}
Comecemos pelo caso
\sqrt{A+\sqrt{B}}=\sqrt{x}+\sqrt{y}
(…)
Esses números [x e y] são (…) as raízes da equação
X^2-AX+\dfrac{B}{4}=0
as quais são dadas pelas expressões:
\dfrac{A+\sqrt{A^2-B}}{2}\qquad\text{e}\qquad\dfrac{A-\sqrt{A^2-B}}{2}.
Podemos agora escolher um destes dois valores para x; o outro será o correspondente valor de y. Como x e y devem ser racionais , sem o que a decomposição , que se pretende, deixa de existir, é necessário que A^2-B seja um quadrado perfeito. (…) se pusermos \sqrt{A^2-B}=C, será C um número racional e o mesmo se poderá dizer dos números
\dfrac{A+C}{2}\qquad\text{e}\qquad\dfrac{A-C}{2}
que são as soluções da equação. (…)
Consideremos agora o caso  
\sqrt{A-\sqrt{B}}=\sqrt{x}-\sqrt{y}
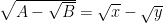(…) O valor de x deverá, aqui, ser \dfrac{A+C}{2} para que a diferença
\sqrt{x}-\sqrt{y}=\sqrt{\dfrac{A+C}{2}}-\sqrt{\dfrac{A-C}{2}}
resulte positiva, visto ser positivo o radical \sqrt{A-\sqrt{B}} que lhe é igual.  »
Este resultado permitiu-me facilmente chegar à solução do problema publicado nesta minha entrada, como expliquei aqui.
Actualização de 20-12-2009: acrescentada figura do livro e referidas as páginas onde a transformação é tratada.
Adenda de 23-5-2011: Em comentário abaixo andreelopess indica a sequinte igualdade 
\dfrac{3}{\sqrt{7-2\sqrt{10}}}+\dfrac{4}{\sqrt{8+4\sqrt{3}}}=\dfrac{1}{\sqrt{11-2\sqrt{30}}}\qquad (\ast)
que, por racionalização de denominadores, se transforma em
\sqrt{7+2\sqrt{10}}+\sqrt{8-4\sqrt{3}}=\sqrt{11+2\sqrt{30}}\qquad (\ast\ast)
Aplicando o método exposto conclui-se que
\sqrt{7+2\sqrt{10}}=\sqrt{5}+\sqrt{2}
\sqrt{8-4\sqrt{3}}=\sqrt{6}-\sqrt{2}
\sqrt{11+2\sqrt{30}}=\sqrt{6}+\sqrt{5}
pelo que efectivamente se tem (\ast\ast). Depois de cálculos fastidiosos concluo  ser equivalente a
\left( 2+\sqrt{2}\sqrt{5}+2\sqrt{14-7\sqrt{3}+4\sqrt{2}\sqrt{5}-2\sqrt{3}\sqrt{2}\sqrt{5}}-2\sqrt{3}\right) ^{2}=30
que confrontei com o resultado em Wolfram Alpha: aqui
Adenda de 24-5-2011: Como escrevo em baixo Sem utilizar o método exposto no post é fácil não digo encontrar, mas justificar as relações numéricas, depois de conhecida a decomposição. Basta elevar ao quadrado ambos os membros.
Fonte:problemasteoremas.wordpress.com
Posted by on
Marcadores:

Nenhum comentário:

Postar um comentário

Assinar: Postar comentários (Atom)