Múltiplos e divisores de um número

Um número é múltiplo de outro quando, ao dividirmos o primeiro pelo segundo, o resto é zero.

O número 10 é múltiplo de 2; pois 10 dividido por 2 é igual a 5 e resta zero.
O número 12 é múltiplo de 3; pois 12 dividido por 3 é igual a 4 e resta zero.
O número 15 também é múltiplo de 3; pois 15 dividido por 3 é igual a 5 e resta zero.
O número 9 não é múltiplo de 2; pois 9 dividido por 2 é igual a 4 e resta 1.
O número 15 não é múltiplo de 4; pois 15 dividido por 4 é igual a 3 e resta 3.

Vamos agora escrever o conjunto dos múltiplos de 2, indicado por M(2), e dos múltiplos de 5, isto é, M(5):

M(2) = {0,2,4,6,8,…}.
M(5) = {0,5,10,15,20,…}
M(3) = {3 x 0, 3 x 1, 3 x 2, 3 x 3, 3 x 4, 3 x 5, 3 x 6,…} = {0,3,6,9,12,15,18,…} Observe também que o menor múltiplo de todos os números é sempre o zero. Diremos que um número é divisor de outro se o segundo for múltiplo do primeiro.
No exemplo anterior, observamos que o número 10 é múltiplo de 2, conseqüentemente 2 é divisor de 10.
Os números 12 e 15 são múltiplos de 3, portanto, 3 e 5 são divisores de 12 e 15, respectivamente. Vamos agora escrever o conjunto dos divisores de 15, indicado por D(15), e dos divisores de 20, isto é, D(20): D(15) = {1,3,5,15}
D(20) = {1,2,4,5,10,20}
Observe que o conjunto dos divisores de um número Natural não-nulo é sempre um conjunto finito, em que o menor elemento é o 1 e o maior é o próprio número. OBSERVAÇÃO: Quando um número é múltiplo de mais de um número, dizemos que o primeiro é um múltiplo comum dos segundos números.Exemplo:

múltiplos de 2: 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20,……

múltiplos de 3: 0, 3, 6, 9, 12, 15, 18, 21, 24,….

múltiplos comuns de 2 e 3: 0, 6, 12, 18,….

Agora é com vocês!!!

EXERCÍCIOS:4 - Calcule os múltiplos de 4, 5, 6, 7, 8 e 9.
5 - Calcule os múltiplos comuns de 3 e 4, 3 e 5, 4 e 5.
6 - Calcule os divisores de 8, 9, 12, 18 e 24.
7 - Qual é o número que é múltiplo de qualquer número?
8 - Qual é o número que é divisor de qualquer número?
9 - O conjunto dos múltiplos de um número é finito ou infinito?
10 - Como devemos proceder para saber se um número é divisor de outro?

---

Divisibilidades

28 de abril de 2009

Divisores de um número

Quando um número é múltiplo de outro, este chama-se divisor do primeiro.

Por exemplo:

· 8 é múltiplo de 4, então 4 é divisor de 8

· 6 é múltiplo de 3, então 3 é divisor de 6

· 12 não é múltiplo de 5, então 5 não é divisor de 12

Indicamos divisores por D

D(12) = {1, 2, 3, 4, 6, 12}

Exercícios

1 – Escreva os divisores dos seguintes números

a) 4

b) 5

c) 7

d) 9

e) 10

f) 18

2 – Qual é o menor e o maior divisor de um número?

fonte: Cruz Junior Florisvaldo

---

Os planetas do Sistema Solar

Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso

Colégio Estadual Dinah Gonçalves

email accbarroso@hotmail.com

 www.ensinodematemtica.blogspot.com.br

www.accbarrosogestar.blogspot.com.br 

    www.youtube.com/accbarroso1
Os planetas do Sistema Solar



São oito os planetas clássicos do Sistema Solar. Na ordem de afastamento do Sol, são eles: Mercúrio, Vênus, Terra, Marte, Júpiter, Saturno, Urano e Netuno.

A partir dos avanços tecnológicos que possibilitaram a observação do céu com instrumentos ópticos como lunetas, telescópios e outros, os astrônomos vêm obtendo informações cada vez mais precisas sobre os planetas e seus satélites. Vamos conhecer um pouco a respeito de cada um desses oito planetas do Sistema Solar.






Mercúrio



É o planeta mais próximo ao Sol e o menor do Sistema Solar. É rochoso, praticamente sem atmosfera, e a sua temperatura varia muito, chegando a mais de 400ºC positivos, no lado voltado para o Sol, e cerca de 180ºC negativos, no lado oposto. Mercúrio não tem satélite. É o planeta que possui um movimento de translação de maior velocidade (o ano mercuriano tem apenas 88 dias). O aspecto da superfície é parecido com o da nossa Lua, toda coberta de crateras, originadas da colisão com corpos celestes.





Vênus



Vênus é conhecido como Estrela-D'Alva ou Estrela da tarde por causa de seu brilho e também porque é visível ao amanhecer e ao anoitecer, conforme a época do ano (mas lembre-se que ela é um planeta e não uma estrela).

É o segundo planeta mais próximo do Sol e o planeta mais próximo da Terra. As perguntas intrigantes que este planeta "gêmeo" da Terra nos coloca começam com o seu movimento de rotação própria. Uma rotação completa sobre si mesmo demora 243.01 dias, o que é um período invulgarmente longo. Além disso, enquanto que a maior parte dos planetas rodam sobre si próprios no mesmo sentido, Vênus é uma das exceções. Tal como Urano e Plutão, a sua rotação é retrógrada, o que significa que em Vênus o Sol nasce a leste e põe-se a oeste.
Vênus é um planeta muito parecido com a Terra, em tamanho, densidade e força da gravidade à superfície, tendo-se chegado a especular sobre se teria condições favoráveis à vida. Além disso, suas estruturas são muito parecidas: um núcleo de ferro, um manto rochoso e uma crosta. Hoje sabemos que, apesar de ter tido origens muito semelhantes à Terra, a sua maior proximidade ao Sol levou a que o planeta desenvolvesse um clima extremamente hostil à vida. De fato, Vênus é o planeta mais quente do sistema solar, sendo mesmo mais quente do que Mercúrio, que está mais próximo do Sol. A sua temperatura média à superfície é de 460ºC devido ao forte efeito de estufa que acontece em grande escala em todo o planeta e não apresenta água.

Terra
É o terceiro planeta mais próximo do Sol. É rochoso e a sua atmosfera é composta de diferentes tipos de gases, e a sua temperatura média é de aproximadamente 15ºC.

A Terra, até o que se sabe, é o único planeta do Sistema Solar que apresenta condições que possibilitam a existência de seres vivos como os conhecemos. Tem um satélite, a Lua.
www.sobiologia.com.br

Sistema Solar

Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso

Colégio Estadual Dinah Gonçalves

email accbarroso@hotmail.com

 www.ensinodematemtica.blogspot.com.br

www.accbarrosogestar.blogspot.com.br 

     

Outros astros do Sistema Solar



Satélites

Até 1610 o único satélite conhecido era o da Terra - a Lua. Naquela ocasião, Galileu Galilei (1564-1642), com a sua luneta, descobriu satélites na órbita do planeta Júpiter. Hoje se sabe da existência de dezenas de satélites.

Na Astronomia, satélite natural é um corpo celeste que se movimenta ao redor de um planeta graças a força gravitacional. Por exemplo, a força gravitacional da Terra mantém a Lua girando em torno do nosso planeta.

Os satélites artificiais são objetos construídos pelos seres humanos. O primeiro satélite artificial foi lançado no espaço em 1957. Atualmente há vários satélites artificiais ao redor da Terra.

O termo "lua" pode ser usado como sinônimo de satélite natural dos diferentes planetas.





Cometas



Cometa Halley

Um cometa é o corpo menor do sistema solar, semelhante a um asteróide, possui uma parte sólida, o núcleo, composto por rochas, gelo e poeira e têm dimensões variadas (podendo ter alguns quilômetros de diâmetro). Geralmente estão distantes do Sol e, nesse caso, não são visíveis. Eles podem se tornar visíveis à medida que, na sua longa trajetória, se aproximam do Sol sublimando o gelo do núcleo e liberando gás e poeira para formar a cauda e a "cabeleira" em volta do núcleo. O mais conhecido dele é o Halley, que regularmente passa pelo nosso Sistema Solar. De 76 em 76 anos, em média, ele é visível da Terra. Ele passou pela região do Sistema Solar próxima do nosso planeta, em 1986, o que possibilitou a sua visibilidade, portanto, o Halley deverá estar de volta em 2062.

/www.sobiologia.com.br/

Critério de Divisibilidade

Critérios de divisibilidade

Para alguns números como o dois, o três, o cinco e outros, existem regras que permitem verificar a divisibilidade sem se efetuar a divisão. Essas regras são chamadas de critérios de divisibilidade.

Divisibilidade por 2
Um número natural é divisível por 2 quando ele termina em 0, ou 2, ou 4, ou 6, ou 8, ou seja, quando ele é par.

Exemplos:
1) 5040 é divisível por 2, pois termina em 0.
2) 237 não é divisível por 2, pois não é um número par.

Divisibilidade por 3
Um número é divisível por 3 quando a soma dos valores absolutos dos seus algarismos for divisível por 3.

Exemplo:
234 é divisível por 3, pois a soma de seus algarismos é igual a 2+3+4=9, e como 9 é divisível por 3, então 234 é divisível por 3.

Divisibilidade por 4
Um número é divisível por 4 quando termina em 00 ou quando o número formado pelos dois últimos algarismos da direita for divisível por 4.

Exemplo:
1800 é divisível por 4, pois termina em 00.
4116 é divisível por 4, pois 16 é divisível por 4.
1324 é divisível por 4, pois 24 é divisível por 4.
3850 não é divisível por 4, pois não termina em 00 e 50 não é divisível por 4.


Divisibilidade por 5
Um número natural é divisível por 5 quando ele termina em 0 ou 5.

Exemplos:
1) 55 é divisível por 5, pois termina em 5.
2) 90 é divisível por 5, pois termina em 0.
3) 87 não é divisível por 5, pois não termina em 0 nem em 5.


Divisibilidade por 6
Um número é divisível por 6 quando é divisível por 2 e por 3.

Exemplos:
1) 312 é divisível por 6, porque é divisível por 2 (par) e por 3 (soma: 6).
2) 5214 é divisível por 6, porque é divisível por 2 (par) e por 3 (soma: 12).
3) 716 não é divisível por 6, (é divisível por 2, mas não é divisível por 3).
4) 3405 não é divisível por 6 (é divisível por 3, mas não é divisível por 2).


Divisibilidade por 8
Um número é divisível por 8 quando termina em 000, ou quando o número formado pelos três últimos algarismos da direita for divisível por 8.

Exemplos:
1) 7000 é divisível por 8, pois termina em 000.
2) 56104 é divisível por 8, pois 104 é divisível por 8.
3) 61112 é divisível por 8, pois 112 é divisível por 8.
4) 78164 não é divisível por 8, pois 164 não é divisível por 8.


Divisibilidade por 9
Um número é divisível por 9 quando a soma dos valores absolutos dos seus algarismos for divisível por 9.

Exemplo:
2871 é divisível por 9, pois a soma de seus algarismos é igual a 2+8+7+1=18, e como 18 é divisível por 9, então 2871 é divisível por 9.


Divisibilidade por 10
Um número natural é divisível por 10 quando ele termina em 0.

Exemplos:
1) 4150 é divisível por 10, pois termina em 0.
2) 2106 não é divisível por 10, pois não termina em 0.


Divisibilidade por 11
Um número é divisível por 11 quando a diferença entre as somas dos valores absolutos dos algarismos de ordem ímpar e a dos de ordem par é divisível por 11.

O algarismo das unidades é de 1ª ordem, o das dezenas de 2ª ordem, o das centenas de 3ª ordem, e assim sucessivamente.

Exemplos:
1) 87549
Si (soma das ordens ímpares) = 9+5+8 = 22
Sp (soma das ordens pares) = 4+7 = 11
Si-Sp = 22-11 = 11
Como 11 é divisível por 11, então o número 87549 é divisível por 11.

2) 439087
Si (soma das ordens ímpares) = 7+0+3 = 10
Sp (soma das ordens pares) = 8+9+4 = 21
Si-Sp = 10-21
Como a subtração não pode ser realizada, acrescenta-se o menor múltiplo de 11 (diferente de zero) ao minuendo, para que a subtração possa ser realizada: 10+11 = 21. Então temos a subtração 21-21 = 0.
Como zero é divisível por 11, o número 439087 é divisível por 11.


Divisibilidade por 12
Um número é divisível por 12 quando é divisível por 3 e por 4.

Exemplos:
1) 720 é divisível por 12, porque é divisível por 3 (soma=9) e por 4 (dois últimos algarismos, 20).
2) 870 não é divisível por 12 (é divisível por 3, mas não é divisível por 4).
3) 340 não é divisível por 12 (é divisível por 4, mas não é divisível por 3).


Divisibilidade por 15
Um número é divisível por 15 quando é divisível por 3 e por 5.

Exemplos:
1) 105 é divisível por 15, porque é divisível por 3 (soma=6) e por 5 (termina em 5).
2) 324 não é divisível por 15 (é divisível por 3, mas não é divisível por 5).
3) 530 não é divisível por 15 (é divisível por 5, mas não é divisível por 3).


Divisibilidade por 25
Um número é divisível por 25 quando os dois algarismos finais forem 00, 25, 50 ou 75.

Exemplos:
200, 525, 850 e 975 são divisíveis por 25.

Antonio Carlos Carneiro Barroso
Extraido do somatematica

Problemas em N

1) Para calcular a quantidade de cadeiras que você vê, podemos usar uma adição ou uma multiplicação.



O resultado é :
4 + 4+ 4 + 4= ou 4 x 4 =

2) Quantas rodas há na figura?
Para saber quantas rodas há na figura, você pode usar a multiplicação.

O resultado é :
2 + 2 + 2 + 2 = ou 4 x 2 =


3) Vamos contar as carteiras da sala de aula? Faça isso usando multiplicação e adição correspondente.



O resulatdo é ?
5 + 5 + 5 = ou 5 x 3 =


4)Um pedreiro empilhou tijolos, como mostra a figura:
Quantos tijolos ele empilhou?Para calcular, use multiplicação e adição correspondente:


Quantos tijolos ele empilhou?
8 + 8 + 8 + 8 + 8 = ou 8 x 5 =
www.colegioweb.com.br

MMC e MDC

(M.D.C) E (M.M.C).

MÁXIMO DIVISOR COMUM



O maior dos divisores comuns de dois ou mais números chama-se máximo divisor comum (m.d.c)

exemplos

consideremos os conjuntos dos divisores de 12 e 18

D12 = { 1,2,3,4,6,12}
D18 = { 1,2,3,6,9,18}

Os mesmos divisores ou números que aparecem em D12 e D18 são { 1,2,3,6} , os números ou divisores {4,9,12,18} aparecem mas não é comum nos dois divisores.

E o maior desses divisores comuns neste caso é 6 e indicamos m.d.c (12,18) = 6


exercícios

1) escreva o conjunto dos divisores de 8,9,10,12,15 e 20

a) D8={
b) D9={
c) D10= {
d) D12={
e) D15={
f) D20 ={

Processos práticos para determinação do mdc

a) Por decomposição em fatores primos (fatoração completa)

exemplo

determinar o mdc de 18 e 60

18 I 2
09I 3
03I 3
01


60 I 2
30 I 2
15 I 3
05 I 5
01 I


18 = 2 x 3 x 3
60 = 2 x 2 x3 x 5

comum nas duas fatorações é um número 2 e um número 3
sendo assim 3 x 2 = 6 o m.d,c,(18,60)= 6

exercício

1) determine o m.d.c.

a) m.d.c (9,12)
b) m.d.c.(8,20)
c) m.d.c.(10,15)
d) m.d.c.(9,12)
e) m.d.c.(10,20)
f) m.d.c.( 15,20)
g) m.d.c.(48,18)
h) m.d.c.(30,18)
i) m.d.c.(60,36)
j) m.d.c.(30,15)
l) m.d.c.(80,48)
m) m.d.c.(3,15,12)
n) m.d.c.(20,6,14)


NÚMEROS PRIMOS ENTRE SI

Quando o m.d.c. de dois números é igual, a 1 dizemos que eles são primos entre si

exemplos:

a) 4 e 9 são primos entre si, pois m.d.c.(4,9)= 1

b) 8 e 15 são primos entre si pois o m.d.c.(8,15) = 1





MÍNIMO MÚLTIPLO COMUM




O menor dos múltiplos comuns (excluído o zero) de dois ou mais números chama-se mínimo múltiplo comum (m. m. c.)

exemplo:

consideramos os conjuntos dos múltiplos de 2 e 3

M2 = { 0,2,4,6,8,10,12..........}

M3 = { 0,3,6,9,15..........}

obtemos o múltilplo comum fazendo a intersecção dos conjuntos

M2 e M3 = { 0, 6 , 12 ...}

excluindo o zero, o menor múltiplo comum é 6. e indicamos o mínimo múltiplo comum de 2 e 3 assim: m.m.c.(2,3) = 6

PROCESSO PRÁTICO PARA DETERMINAR O m.m.c.

Por decomposição em fatores primos (fatoração completa)

1) determinar o m.m.c. de 120 e 80

120,80 I 2060,40 I 2
030,20 I 2
015,10 I 2
015,05 I 3
005,05 I 5001,01

2 x 2 x 2 x 2 x 3 x 5 = 240

logo m.m.c. (120,80) = 240

2) determinar o m.m.c. de 14, 45 e 6

14, 45, 06 I 207, 45, 03 I 3
07, 15, 01 I 307, 05, 01 I 5
07, 01, 01 I 7
01, 01, 01 I

2 x 3 x 3 x5 x7 = 630

logo m.m.c ( 14, 45, 06) = 630


EXERCÍCIOS

1) Determine o m.m.c. pelo processo da decomposição

a) m.m.c.(15,18)
b) m.m.c.(10,12)
c) m.m.c.(10,6,15)
d) m.m.c( 12,20,3)
e) m.m.c(15,3)
f) m.m.c.( 10,15)
g) m. m. c. ( 18, 30)
h) m.m.c. ( 21, 12 )
i) m.m.c. ( 35,10)
j) m.m.c. ( 25, 80)
l) m.m.c.( 140,10)
m) m.m.c ( 8,10,25)
n) m.m.c.( 3,12,32)
o) m.m.c.(2,3,5,10)
p) m.m.c. ( 18, 24, 36)

2) Determine o m.m.c

a) m.m.c. ( 50,75)
b) m.m.c. ( 60,24)
c) m.m.c. ( 21,30)
d) m.m.c. ( 28,48)
e) m.m.c ( 2,4)
f) m.m.c. ( 7,5)
g) m.m.c. ( 9,1)
h) m.m.c.( 21,7)
i) m.m.c. ( 8,9)
j) m.m.c. ( 13,26)
l) m.m.c ( 2,4,6)
m) m.m.c. ( 3,6,9)
n) m.m.c. ( 10,12,45)
o) m.m.c ( 6,8,12,15)
p) m.m.c ( 12,18,36,40)




3) calcule o m.m.c.

a) m.m.c (4,6,9,15)
b) m.m.c. ( 2,10,15,45)
c) m.m.c.(8,36,28,72)
d) m.m.c( 45,96,10,180)
e) m.m.c( 20,30,48,120)
f) m.m.c( 7,2)
g) m.m.c( 8,10)
h) m.m.c ( 14,21)
i) m.m.c ( 50 ,25)
j) m.m.c ( 40 , 60 )
l) m.m.c.( 80,56)
m) m.m.c ( 2,3,4)
n) m.m.c. ( 4,6,8)
o) m.m.c. ( 6,8,12)
p) m.m.c.(4,8,16)
q) m.m.c ( 12, 18, 36)
r) m. m.c ( 12, 10, 8)
s) m.m.c ( 6,8,10,12)

4) Usando a decomposição em fatores primos, determine:

a) m.m.c (10,12) (R:60)
b) m.m.c. ( 6,10,15) (R: 30)
c) m.m.c. ( 14,21,30) (R: 210)
d) m.m.c. ( 100, 150, 200) (R: 600)
e) m.m.c. (70,110) (R: 770)
f) m.m.c. (30, 75) (R:150)
g) m.m.c. (18,60) (R: 180)
h) m.m.c. (21, 35,84) (R: 420)
i) m.m.c. ( 66, 102) (R: 1122)
j) m.m.c. ( (90, 36, 54) (R: 540)
l) m.m.c. ( 48, 20, 40, 36) (R: 720)

Decomposição em fatores primos

Todo número natural, maior que 1, pode ser decomposto num produto de dois ou mais fatores.

Decomposição do número 24:
24 = 2 x 2 x 3 x 2

Decomposição do número 50:
50 = 2 x 5 x 5
50 = 5 x 2 x 5

Decomposição do numero 20:
20 = 2 x 5 x 2
20 = 5 x 2 x 2

Decomposição do número 50:
50 = 2 x 5 x 5.
50 = 5 x 2 x 5.

Agora, descubra qual é o número de cada decomposição:

a) 2 x 3 x 5 =

b) 2 x 5 =

c) 2 x 5 x 5 =

d) 2 x 3 x 7 =

e) 3 x 3 x 5 =

Propriedades da Multiplicação

Fechamento: A propriedade de fechamento é satisfeita, pois o produto de dois números naturais ainda é um número natural.

Associatividade: Na multiplicação de três ou mais números naturais quaisquer, podemos associar os fatores de diferentes modos que o produto é sempre o mesmo. A propriedade de associatividade é satisfeita na multiplicação, pois:

por exemplo:


3.5.2 =15.2 =30


3.(5.2) =3.10 =30

Observe que os resultados obtidos são iguais. Os parênteses indicam a multiplicação que deve ser feita primeiro.

Existência de Elemento Neutro: O elemento neutro na multiplicação é o número 1, pois qualquer número natural multiplicado por 1 é esse próprio número natural.

Por exemplo: 8 x 1 = 8 e 1 x 8 = 8

Comutatividade: A propriedade comutativa também é satisfeita pela multiplicação, pois a ordem dos fatores não altera o produto.

Observe:

7 x 5 = 35 5 x 7 = 35
4 x 5 = 20 5 x 4 = 20

Distributividade: Um jeito simples de explicar a propriedade distributiva é com o seguinte exemplo, tenho 3 laranjas e ganho mais 5 laranjas então na verdade eu fiquei com (3 + 5) laranjas agora substituímos as laranjas por um número, por exemplo, o número 6.
Assim temos, 3.6 + 5.6 = (3 + 5) . 6.

Operações com decimais

Número decimal é aquele número que tem parte inteira e parte decimal, essas são separadas por vírgula.
As quatro operações (adição, subtração, multiplicação e divisão) com os números decimais, para resolver é necessário utilizar algumas regras.

Adição

Para adicionarmos dois ou mais números decimais é preciso colocar vírgula em baixo de vírgula.
Para fazermos qualquer adição, devemos saber que os números somados são chamados de parcelas e o resultado de soma total e que as parcelas tem que ser adicionadas da maior pela menor.

►4,879 + 13,14 → Parcelas

1
13 , 140 → Acrescentamos o zero para completar casas decimais.
+4 , 879
18 , 019 → Soma total

Na soma de 4 centésimos com 7 centésimos é igual a 11 centésimos, assim fica um e “vai um”.

► 2 + 1, 751

2 , 000 → Acrescentamos o zero para completar casar decimais.
+1 , 751
3 , 751

►0,3 + 1

1 , 0
+ 0 , 3
1 , 3

Subtração

Para subtrairmos dois números decimais, devemos da mesma forma que na adição colocar vírgula de baixo de vírgula de vírgula.
Sendo que o diminuendo deve ser sempre maior que o subtraendo e o resultado recebem o nome de resto ou diferença.

• 7,37 – 2,8 → minuendo e subtraendo nessa mesma ordem.

6 13
7 , 3 7 → Minuendo
- 2 , 8 0 → Subtraendo → acréscimo do zero para completar casas decimais.
4 , 5 7 → Resto ou Diferença

Para subtrair 8 décimos, transformamos 1 inteiro em 10 décimos, ficando com 13 décimos no minuendo. Assim fazemos:
13 – 8 = 5
6 – 2 = 4

► 0,25 - 0,18

1 15
0 , 2 5
- 0 , 1 8
0 , 0 7

Pra subtrair 8, transformamos 1 décimo em 10 centésimos, ficando com 15 o minuendo. Assim fazemos:
15 – 8 = 7
1 – 1 = 0

Fração exercícios

01 – Com 12 litros de leite, quantas garrafas de 2/3 de litros poderão ser cheias ?

02 – Coriolano faz um cinto com 3/5 de um metro de couro. Quantos cintos poderão ser feitos com 18 metros de couro ?

03 – Qual é o número cujos 4/5 equivalem a 108 ?

04 – Distribuíram-se 3 1/2 quilogramas de bombons entre vários meninos. Cada um recebeu 1/4 de quilograma. Quantos eram os meninos ?

05 – Para ladrilhar 2/3 de um pátio empregaram-se 5 456 ladrilhos. Para ladrilhar 5/8 do mesmo pátio, quantos ladrilhos seriam necessários ?

06 – Dona Solange pagou R$ 5.960,00 por 4/7 de um terreno. Quanto pagaria por 4/5 desse terreno?

07 – Luciano fez uma viagem de 1.210 km, sendo 7/11 de aeroplano; 2/5 do resto, de trem, 3/8 do novo resto, de automóvel e os demais quilômetros, a cavalo. Calcular quantos quilômetros percorreu a cavalo ?

08 – A terça parte de um número adicionado a seus 3/5 é igual a 28. Calcule a metade desse número ?

09 – Carolina tinha R$ 175,00. Gastou 1/7 de 1/5 dessa importância. Quanto sobrou ?

10 – Que número é necessário somar a um e três quartos para se obter cinco e quatro sétimos ?

11 – A soma de dois números é 850. Um vale 12/5 do outro. Quais são eles ?

12 – Se dos 2/3 de um número subtrairmos seus 3/7, ficaremos com 45. Qual é o número?

13 – A soma de três números é 30. O primeiro corresponde aos 2/3 do segundo e este, aos 3/5 do terceiro. Calcular o produto destes três números.

14 – Se 7/8 de um terreno valem R$ 21.000,00, qual é o valor de 5/48 do mesmo terreno?

15 – Qual é o número que se da metade subtrairmos 8 unidades ficaremos com 1/3 dele mesmo ?

16 – Da terça parte de um número subtraindo-se 12, fica-se com 1/6 do mesmo número. Que número é esse ?

17 – Qual é o número que retirando 48 unidades de sua metade, encontramos a sua oitava parte ?

18 – A diferença entre dois números é 90; um é 3/13 do outro. Calcular os números.

19 – A soma de dois números é 345; um é 12/11 do outro. Calcule-os.

20 – Seu Áureo tendo gasto 4/7 do dinheiro que possuía, ficou com 1/3 dessa quantia mais R$ 164,00. Quanto tinha o velho Áureo?

21 – Divida R$ 1590,00 em três partes de modo que a primeira seja 3/4 da segunda e esta 4/5 da terceira.

22 – Se eu tivesse apenas 1/5 do que tenho, mais R$ 25,00. teria R$ 58,00. Quanto tenho ?

23 – A nona parte do que tenho aumentada de R$ 17,00 é igual a R$ 32,50. Quanto possuo ?

24 – Zé Augusto despendeu o inverso de 8/3 de seu dinheiro e ficou com a metade mais R$ 4,30. Quanto possuía ?

25 – Repartir 153 cards em três montes de forma que o primeiro contenha 2/3 do segundo o qual deverá ter 3/4 do terceiro.

26 – Distribuir 3.717 tijolos por três depósitos de tal maneira que o primeiro tenha 3/4 do segundo e este 5/6 do terceiro.

27 – O diretor de um colégio quer distribuir os 105 alunos da 4ª série em três turmas de modo que a 1ª comporte a terça parte do efetivo; a 2ª, 6/5 da 1ª, menos 8 estudantes e a 3ª, 18/17 da 2ª. Quantos alunos haverá em cada turma ?

28 – Dividiu-se uma certa quantia entre três pessoas. A primeira recebeu 3/5 da quantia, menos R$ 100,00; a segunda, 1/4 , mais R$ 30,00 e a terceira, R$ 160,00. Qual era a quantia ?

29 – Um número é tal que, se de seus 2/3 subtrairmos 1.036, ficaremos com 4/9 do mesmo. Que número é esse?

30 – Das laranjas de uma caixa foram retirados 4/9, depois 3/5 do resto, e ficaram 24 delas. Quantas eram as laranjas ?

31 – Marieta tinha R$ 240,00. Gastou um quinto dessa quantia, e, depois, a terça parte do resto. Com quanto ficou ?

32 – Repartir R$ 671,00 entre três pessoas de modo que a primeira seja contemplada com 2/5 do que receber a segunda e esta, 3/8 do receber a terceira.

33 – Dividir R$ 480,00 por três pessoas, de modo que as partes da primeira e da segunda sejam, respectivamente, 1/3 e 4/5 da parte a ser recebida pela terceira

34 – Argemiro tinha R$ 375,00. Despendeu 2/5, menos R$ 6,00; depois a terça parte do resto, mais R$ 18,00. Quanto sobrou ?

35 – Um reservatório é alimentado por duas torneiras. A primeira pode enchê-lo em 15 horas e a segunda, em 12 horas. Que fração do reservatório encherão em uma hora, as duas juntas ?

36 – Uma torneira enche um reservatório em 2 horas e outra em 3 horas. Ambas, em que tempo enchê-lo-ão ?

37 – Uma torneira enche uma cisterna em 1/8 da hora e uma válvula o esvazia em 1/4 da hora. Abertas, em que tempo o reservatório ficará completamente cheio ?

38 – Uma torneira enche um depósito d’água em 1/14 da hora enquanto uma válvula pode esvaziá-lo em 1/9 da hora. Trabalhando juntas, em quanto tempo o líquido contido no depósito atingirá seus 5/6 ?

39 – Um reservatório é alimentado por duas torneiras. A primeira pode enchê-lo em 15 horas e a segunda, em 10 horas. A primeira é conservada aberta durante 2/3 da hora e a segunda durante 1/2 hora. Que fração do reservatório ficará cheia ?

40 – Claudia fez 2/9 de um trabalho em 12 horas e Mariana, 4/7 do resto em 8 horas. Quantas horas levarão para fazer a mesma obra, se trabalharem juntas ?

41 – Taninha fez 2/5 de um bordado em 8 horas e Clarisse, 1/3 do resto em 6 horas. Em quanto tempo poderão concluí-lo, se trabalharem juntas ?

42 – Vó Marieta é capaz de fazer um bordado em 16 horas e tia Celeste, 5/7 do resto em 15 horas. Em quanto tempo aprontarão o bordado todo, se operarem juntas ?

43 – Roberval, um investidor no mercado de capitais, perdeu a quarta parte de um capital. Em outros negócios, ganhou o quíntuplo de R$ 30.000,00. Sendo a fortuna atual o dobro do capital inicial. Que capital era esse ?

44 – Um quitandeiro vendeu ao primeiro freguês 3/5 das melancias que tinha, mais quatro, e ao segundo, 1/3, também do total. Tendo o primeiro ficado com mais duas dúzias de melancias do que o outro, pergunta-se quantas melancias o comerciante possuía e com quantas ficou ?

45 – Andréa tem 2/9 do dinheiro necessário para comprar um apartamento, e seu marido, 3/11 dessa quantia. Se a essa importância o casal adicionar R$ 3.500,00 poderão comprar a casa própria. Qual é o preço do imóvel ? Quanto tem cada um deles ?

46 – Uma torneira enche um reservatório em 6 horas e outra, em 2 horas. Ambas, funcionando conjuntamente, em que tempo encherão o reservatório ?

47 – Uma torneira enche um tanque em duas horas e outra o esvazia em dez horas. O tanque estando vazio e abrindo-se as duas torneiras, em que tempo ficará ele completamente cheio ?

48 – Silvana executa um bordado em nove horas de trabalho e Fernanda, em doze horas. Com auxílio de Eliane, aprontam-no em quatro horas. Calcular o tempo em que Eliane faria o mesmo bordado sozinha.

49 – Alfredo pode pintar uma casa em sete horas de trabalho e seu irmão, em cinco horas. Juntos, que fração do trabalho executarão em uma hora ? Em quanto tempo farão todo a pintura da casa ?

50 – Um trem partiu do Rio com um certo número de passageiros. Na primeira parada, saltaram 3/7 dos passageiros e na quarta entraram 40 pessoas. Em outras estações saltaram 5/8 dos passageiros restantes. O trem chegou à estação final com 36 passageiros. Com quantos passageiros o trem partiu do Rio ?

51 – Um número vale 8/5 de um segundo ou 2/3 de um terceiro. Calcular os três números sabendo que sua soma é igual a 500.

52 – Cuidadosamente, Severina, a empregada dos “Cavalcante” arruma uma bela cesta de maçãs. O patriarca ao ver as maçãs toma para si 1/6 das frutas, sua esposa pega 1/5 das restantes, o filho mais velho pega para si 1/4 do restante, o filho do meio e o mais novo pegam, respectivamente 1/3 e 1/2 dos restantes. Quando Severina chega e percebe o cesto praticamente vazio, fica magoada com a gulodice dos patrões e decide pegar para si as 3 frutas restantes. Quantas eram as maçãs arrumadas originalmente por Severina ?


Resolução dos problemas

01) 18 garrafas
02) 30 cintos
03) 135
04) 14 meninos
05) 5.115
06) R$ 8.344,00
07) 165 km
08) 15
09) R$ 170,00
10)

11) 600 e 250
12) 189
13) 810
14) R$ 2.500,00
15) 48
16) 72
17) 128
18) 117 e 27
19) 180 e 165
20) R$ 1.722,00
21) R$ 397,50 , R$ 530,00 e R$ 662,50
22) R$ 165,00
23) R$ 139,50
24) R$ 34,40
25) 34 , 51 e 68
26) 945, 1260 e 1512
27) 35 , 34 e 36
28) R$ 600,00
29) 4.682
30) 108
31) R$ 128,00
32) R$ 66,00 , R$ 165,00 e R$ 440,00
33) R$ 75,00 , R$ 180,00 e R$ 225,00
34) R$ 136,00
35) 3/20
36) 1 horas e 12 minutos
37) 1/4 h ou 15 min
38) 1/6 h ou 10 min
39) 17/180
40) 13 h 30 min
41) 12 h
42) h

43) R$ 120.000,00
44) 75 e 1
45) R$ 6.930,00, R$ 1.540,00 e R$ 1.890,00
46) 1h 30 min
47) 2 h 30 min
48) 18 horas
49) 12/35 e 2 h 55 min
50) 98
51) 160 , 100 e 240
52) 18 maçãs

Autoria: Professor Luiz Fernando

MMC e MDC c/ exercícios

Professor de Matemática no Colégio Estadual Dinah Gonçalves

E Biologia na rede privada de Salvador-Bahia

Professor Antonio Carlos carneiro Barroso

email accbarroso@hotmail.com

Blog www.ensinodematemtica.blogspot.com.br e www.accbarroso60.wordpress.com

www.accbarrosogestar.wordpress.com
www.accbarrosogestar.blogspot.com.br
www.youtube.com/accbarroso1

(M.D.C) E (M.M.C).

MÁXIMO DIVISOR COMUM



O mair dos divisores comuns de dois ou mais números chama-se máximo divisor comum (m.d.c)

exemplos

consideremos os conjuntos dos divisores de 12 e 18

D12 = { 1,2,3,4,6,12}
D18 = { 1,2,3,6,9,18}

Os mesmos divisores ou números que aparecem em D12 e D18 são { 1,2,3,6} , os números ou divisores {4,9,12,18} aparecem mas não é comum nos dois divisores.

E o maior desses dovisores comuns neste caso é 6 e indicamos m.d.c (12,18) = 6


exercícios

1) escreva o conjunto dos divisores de 8,9,10,12,15 e 20

a) D8={
b) D9={
c) D10= {
d) D12={
e) D15={
f) D20 ={

Processos práticos para determinação do mdc

a) Por decomposição em fatores primos (fatoração completa)

exemplo

determinar o mdc de 18 e 60

18 I 2
09I 3
03I 3
01


60 I 2
30 I 2
15 I 3
05 I 5
01 I


18 = 2 x 3 x 3
60 = 2 x 2 x3 x 5

comum nas duas fatorações é um número 2 e um número 3
sendo assim 3 x 2 = 6 o m.d,c,(18,60)= 6

exercicio

1) determine o m.d.c.

a) m.d.c (9,12)
b) m.d.c.(8,20)
c) m.d.c.(10,15)
d) m.d.c.(9,12)
e) m.d.c.(10,20)
f) m.d.c.( 15,20)
g) m.d.c.(48,18)
h) m.d.c.(30,18)
i) m.d.c.(60,36)
j) m.d.c.(30,15)
l) m.d.c.(80,48)
m) m.d.c.(3,15,12)
n) m.d.c.(20,6,14)


NÚMEROS PRIMOS ENTRE SI

Quando o m.d.c. de dois números é igual, a 1 dizemos que eles são primos entre si

exemplos:

a) 4 e 9 são primos entre si, pois m.d.c.(4,9)= 1

b) 8 e 15 são primos entre si pois o m.d.c.(8,15) = 1





MÍNIMO MÚLTIPLO COMUM




O menor dos múltiplos comuns (excluído o zero) de dois ou mais números chama-se mínimo múltiplo comum (m. m. c.)

exemplo:

consideramos os conjuntos dos múltiplos de 2 e 3

M2 = { 0,2,4,6,8,10,12..........}

M3 = { 0,3,6,9,15..........}

obtemos o múltilplo comum fazendo a instersecção dos conjuntos

M2 e M3 = { 0, 6 , 12 ...}

excluindo o zero, o menor múltiplo comum é 6. e indicamos o mínimo múltiplo comum de 2 e 3 assim: m.m.c.(2,3) = 6

PROCESSO PRÁTICO PARA DETERMINAR O m.m.c.

Por decomposição em fatores primos (fatoração completa)

1) determinar o m.m.c. de 120 e 80

120,80 I 2060,40 I 2
030,20 I 2
015,10 I 2
015,05 I 3
005,05 I 5001,01

2 x 2 x 2 x 2 x 3 x 5 = 240

logo m.m.c. (120,80) = 240

2) determinar o m.m.c. de 14, 45 e 6

14, 45, 06 I 207, 45, 03 I 3
07, 15, 01 I 307, 05, 01 I 5
07, 01, 01 I 7
01, 01, 01 I

2 x 3 x 3 x5 x7 = 630

logo m.m.c ( 14, 45, 06) = 630


EXERCÍCIOS

1) Determine o m.m.c. pelo processo da decomposição

a) m.m.c.(15,18)
b) m.m.c.(10,12)
c) m.m.c.(10,6,15)
d) m.m.c( 12,20,3)
e) m.m.c(15,3)
f) m.m.c.( 10,15)
g) m. m. c. ( 18, 30)
h) m.m.c. ( 21, 12 )
i) m.m.c. ( 35,10)
j) m.m.c. ( 25, 80)
l) m.m.c.( 140,10)
m) m.m.c ( 8,10,25)
n) m.m.c.( 3,12,32)
o) m.m.c.(2,3,5,10)
p) m.m.c. ( 18, 24, 36)

2) Determine o m.m.c

a) m.m.c. ( 50,75)
b) m.m.c. ( 60,24)
c) m.m.c. ( 21,30)
d) m.m.c. ( 28,48)
e) m.m.c ( 2,4)
f) m.m.c. ( 7,5)
g) m.m.c. ( 9,1)
h) m.m.c.( 21,7)
i) m.m.c. ( 8,9)
j) m.m.c. ( 13,26)
l) m.m.c ( 2,4,6)
m) m.m.c. ( 3,6,9)
n) m.m.c. ( 10,12,45)
o) m.m.c ( 6,8,12,15)
p) m.m.c ( 12,18,36,40)




3) calcule o m.m.c.

a) m.m.c (4,6,9,15)
b) m.m.c. ( 2,10,15,45)
c) m.m.c.(8,36,28,72)
d) m.m.c( 45,96,10,180)
e) m.m.c( 20,30,48,120)
f) m.m.c( 7,2)
g) m.m.c( 8,10)
h) m.m.c ( 14,21)
i) m.m.c ( 50 ,25)
j) m.m.c ( 40 , 60 )
l) m.m.c.( 80,56)
m) m.m.c ( 2,3,4)
n) m.m.c. ( 4,6,8)
o) m.m.c. ( 6,8,12)
p) m.m.c.(4,8,16)
q) m.m.c ( 12, 18, 36)
r) m. m.c ( 12, 10, 8)
s) m.m.c ( 6,8,10,12)

4) Usando a decomposição em fatores primos, determine:

a) m.m.c (10,12) (R:60)
b) m.m.c. ( 6,10,15) (R: 30)
c) m.m.c. ( 14,21,30) (R: 210)
d) m.m.c. ( 100, 150, 200) (R: 600)
e) m.m.c. (70,110) (R: 770)
f) m.m.c. (30, 75) (R:150)
g) m.m.c. (18,60) (R: 180)
h) m.m.c. (21, 35,84) (R: 420)
i) m.m.c. ( 66, 102) (R: 1122)
j) m.m.c. ( (90, 36, 54) (R: 540)
l) m.m.c. ( 48, 20, 40, 36) (R: 720)

MDC

Para estudarmos o máximo divisor comum entre dois termos, precisamos saber o que é divisor de um número. Todo número natural possui divisores, isto é, se ao dividirmos um número A pelo número B e obtermos resto zero podemos afirmar que B é divisor de A. Por exemplo:

16 : 2 é igual a 8 e resto 0.
25 : 5 é igual a 5 e resto 0.

Podemos concluir que 2 e 5 são divisores de 16 e 25 respectivamente.

Exemplos de divisores de um número:

Divisores de:
32 = 1, 2, 4, 8, 16, 32
15 = 1, 3, 5, 15
45 = 1, 3, 5, 9, 15, 45

O MDC entre dois ou mais números é o maior divisor comum a eles.
Exemplos:

MDC(12,36)
Divisores de 12 = 1, 2, 3, 4, 6, 12
Divisores de 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
Podemos verificar que o maior divisor comum entre 12 e 36 é o próprio 12.

MDC(12,24,54)
Divisores de 18 = 1, 2, 3, 6, 9, 18
Divisores de 24 = 1, 2, 3, 4, 6, 8, 12, 24
Divisores de 54 = 1, 2, 3, 6, 18, 27, 54
O maior divisor comum a 12, 24 e 54 é o 6.


Processo prático para a obtenção do máximo divisor comum

MDC(12,36)

Os números destacados na fatoração estão dividindo os dois números ao mesmo tempo, então devemos realizar uma multiplicação entre eles para descobrirmos o máximo divisor comum.
2 x 2 x 3 = 12
MDC(12,36) = 12


MDC(70,90,120)

O máximo divisor comum a 70, 90 e 120 = 2 x 5 = 10
extraido de www.mundoeducacao.com.br

Os estados físicos da água

A água pode ser encontrada em três estados físicos:



A água pode mudar de estado físico como, por exemplo, ir do estado sólido para o líquido. Um exemplo disso é quando deixamos o gelo (estado sólido da água) fora da geladeira e ele derrete virando líquido.

Existem nomes que representam cada uma destas mudanças de estados físicos, veja abaixo quais são:



Para que aconteçam a fusão e a vaporização é necessário fornecer energia – aquecer – a água.
Para que aconteçam a solidificação (mudança de estado liquido para o estado sólido) e a liquefação (do estado gasoso para o liquido) é preciso retirar energia – o calor – da água.
A evaporação da água no seu ciclo natural ocorre à temperatura ambiente e é lenta. A água ferve, do liquido para o gasoso, de forma muito mais rápida, por que ocorre a ebulição.
O ponto de ebulição da água depende também do nível de pressão do ambiente.
Ebulição e vaporação são, na realidade, tipos de vaporização.

O que é água?

Pode até parecer um pouco absurdo fazer esta pergunta, mas o que é a água? Já que todos bebemos água e já a utilizamos para as mais variadas necessidades em infinidáveis momentos da nossa vida. Mas, afinal qual é a composição deste líquido que dá vida a todo o planeta terra? A água é formada por dois átomos de hidrogênio (H2) e por um átomo de oxigênio (O), formando assim, a molécula H2O.

Propriedades da água

* Apresenta praticamente a mesma massa desde que o Planeta se formou.

* É purificada pela evaporação e também pela penetração no solo, até os lençóis freáticos.

* A água potável é cristalina, inodora, incolor e insípida.

* É considerada solvente universal, propiciando a formação de misturas com outras substâncias.

* Pode transportar substâncias e outros corpos.

* Quando em repouso, apresenta sua superfície plana e horizontal.

* Apresenta uma tensão superficial, isto é, capacidade de manter juntas as moléculas de sua superfície.

* Uma torneira que goteja demonstra como a água se apega a si mesma. À medida que a água cai em gotas, cada gota fica um instante pendurada na torneira, estende-se, solta-se, e a seguir forma instantaneamente uma pequena bola. As moléculas da superfície da água mantêm-se tão coesamente ligadas entre si que a água pode sustentar objetos mais pesados que ela. A água salgada apresenta maior densidade do que água doce.

www.colegioweb.com.br

Divisibilidade

www.youtube.com/accbarroso1
Conhecer os critérios de divisibilidade facilita a resolução de cálculos envolvendo divisões. Vejamos alguns critérios de divisibilidade:

DIVISIBILIDADE POR 2

Um número é divisível por 2 quando é par.

Números pares são os que terminam em 0, ou 2, ou 4, ou 6 , ou 8.

Ex : 42 - 100 - 1.445.086 - 8 - 354 - 570

DIVISIBILIDADE POR 3

Um número é divisível por 3 quando a soma dos seus algarismos é divisível por 3.

Ex : 123 (S= 1 + 2 + 3 = 6) - 36 (S=9) - 1.478.391 ( S=33) - 570 (S=1

DIVISIBILIDADE POR 4

Um número é divisível por 4 quando os dois últimos algarismos formam um número divisível por 4.

Ex : 956 - 844 - 1.336 - 120 - 8.357.916 - 752 - 200

DIVISIBILIDADE POR 5

Um número é divisível por 5 quando termina em 0 ou 5 .

Ex : 475 - 800 - 1.267.335 - 10 - 65

DIVISIBILIDADE POR 6

Um número é divisível por 6 quando é divisível por 2 e3 ao mesmo tempo.

Ex : 36 - 24 - 126 - 1476

DIVISIBILIDADE POR 7

Tomar o último algarismo e calcular seu dobro. Subtrair esse resultado do número formado pelos algarismos restantes. Se o resultado for divisível por 7 então, o número original também será divisível por 7.

Ex1 :

238 : 8 x 2 = 16

23 - 16 = 7 : como 7 é divisível por 7 , 238 também é divisível.

693 : 3 x 2 = 6

69 - 6 = 63

63 : 3 x 2 = 6

6 - 6 = 0 : como 0 é divisível por 7, 693 também é divisível.

Ex2 :

235 : 5 x 2 = 10

23 - 10 = 13 : como 13 não é divisível por 7, 235 também não é divisível.

DIVISIBILIDADE POR 8

Um número é divisível por 8 quando os três últimos algarismos formam um número divisível por 8.

Ex : 876.400 - 152 - 245.328.168

DIVISIBILIDADE POR 9

Um número é divisível por 9 quando a soma dos seus algarismos é divisível por 9.

Ex : 36 - 162 - 5463 - 5.461.047

DIVISIBILIDADE POR 10

Um número é divisível por 10 quando termina em 0.

Ex : 100 - 120 - 1.252.780 - 1.389.731.630

DIVISIBILIDADE POR 11

Quando a diferença entre as somas dos algarismos de ordem ímpar e de ordem par, a partir da direita for múltipla de 11.

Ex : 7.973.207

S (ordem ímpar) = 7 + 2 + 7 + 7 = 23

S (ordem par) = 0 + 3 + 9 = 12

diferença = 11

OBS: NÚMERO DE DIVISORES:

O conjunto dos divisores de um número natural x é o conjunto D(x) formado por todos os números naturais que são divisores de x.

Exemplo: o conjunto dos divisores de 36.

D(36) = { 1, 2, 3, 4, 6, 9, 12, 18, 36}
colaweb.com.br

Conjunto

www.youtube.com/accbarroso1
CONCEITO

Conjunto vazio { } ou Ø: um conjunto que não possui elementos.

Subconjuntos: quando todos os elementos de um conjunto A qualquer, pertencem a um outro conjunto B, pode-se dizer, então, que A é um subconjunto de B.

Observações:

- Todo o conjunto A é subconjunto dele próprio;

- O conjunto vazio, por convenção, é subconjunto de qualquer conjunto.

União de Conjuntos: dados os conjuntos A e B, define-se como união dos conjuntos A e B todos os elementos pertencentes a A ou B.

Intersecção de Conjuntos: dados os conjuntos A e B, define-se como intersecção o conjunto formado por todos os elementos pertencentes a A e B, simultaneamente, ou seja:

Diferença de Conjuntos: dados os conjuntos A e B, define-se como diferença entre A e B (nesta ordem) ao conjunto representado por A-B, formado por todos os elementos pertencentes a A, mas que não pertencem a B.

Produto Cartesiano: dados os conjuntos A e B, chama-se produto cartesiano A com B, ao conjunto AxB, formado por todos os pares ordenados (x,y), onde x é elemento de A e y é elemento de B, ou seja:

AxB = {(x,y) / x Є A ou y Є B}

Número de subconjuntos de um conjunto: se um conjunto A possuir n elementos, então existirão 2n subconjuntos de A.



CONJUNTO DOS NÚMEROS NATURAIS (N)

0, 1, 2, 3, 4, 5...



CONJUNTO DOS NÚMEROS INTEIROS (Z)

...-4, -3, -2, -1, 0, 1, 2, 3, 4...



CONJUNTO DOS NÚMEROS RACIONAIS (Q)

Qualquer número que possa ser expresso pela equação a/b desde que seja b ≠ 0: 2/3, 1/5, 5/2 ...

Observação: Existem frações que não possuem representação decimal exata, por exemplo:

5/9 = 0,555...

1/3 = 0,333...

5/3 = 0,833...

Os numerais decimais em que há repetição periódica e infinita de um ou mais algarismos, são chamados de numerais decimais periódicos ou dízimas periódicas.

Em uma dízima periódica, o período é o algarismo ou algarismos que se repetem infinitamente.



DÍZIMAS PERIÓDICAS - CLASSIFICAÇÃO



As dízimas periódicas podem ser simples ou compostas, por exemplo:

Nas DÍZIMAS PERIÓDICAS SIMPLES o período apresenta-se logo após a vírgula:

5/9 = 0,555... (período: 5)

7/3 = 2,333... (período: 3)

4/33 = 0,1212... (período: 12)

Nas DÍZIMAS PERIÓDICAS COMPOSTAS, existe uma paste não periódica entre o período e a vírgula:

1/45 = 0,0222... (Período: 2) Parte não periódica: 0

1.039/900 = 1,15444... (Período: 4) Parte não periódica: 15

61/495 = 0,1232323... (Período: 23) Parte não periódica: 1

Observação: a parte não periódica de uma dízima é o termo situado entre vírgulas e o período, excluímos, portanto, da parte não periódica do inteir.



GERATRIZ DE UMA DÍZIMA PERIÓDICA



A fração (número racional) que deu origem a uma dízima periódica é chamada de geratriz da dízima periódica.

Procedimentos para determinar a geratriz de uma dízima:

Dízima simples

A geratriz de uma dízima simples é uma fração que tem o período como numerador, e para denominador tantos noves quantos forem os algarismos do período, por exemplo:

0,777... = 7/9

0,2323... = 23/99

Dízima composta

A geratriz da dízima composta é uma fração da forma n/d, onde:

n é a parte não periódica seguida do período, menos a parte não periódica, e

d são tantos noves quantos forem os algarismos do período seguidos de tantos zeros quantos forem os algarismos da parte não periódica.

Exemplos:

0,1252525... = 125-1/990 = 124/990

0,047777... = 047-04/900 = 43/900





CONJUNTO DOS NÚMEROS IRRACIONAIS (I)



Os números irracionais são decimais infinitas não periódicas, ou seja, os números que não podem ser escrito na forma de fração (divisão de dois inteiros). Como exemplo de números irracionais, temos a raiz quadrada de 2 e a raiz quadrada de 3:

UM NÚMERO IRRACIONAL BASTANTE CONHECIDO É O NÚMERO
π =3,1415926535...

EXEMPLOS DE NÚMEROS IRRACIONAIS: V2, V5, π



CONJUNTO DOS NÚMEROS COMPLEXOS



Número complexo é todo número que pode ser escrito na forma

z = a + b i

onde a e b são números reais e i é a unidade imaginária.

O número real a é a parte real do número complexo z e o número real b é a parte imaginária do número complexo z, denotadas por:

a = Re(z) e b = Im(z)

Números naturais operações

www.youtube.com/accbarroso1

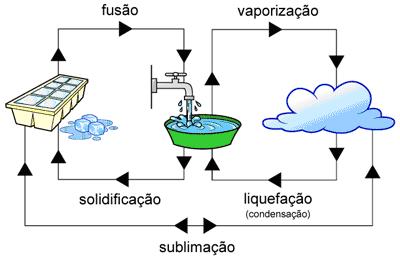
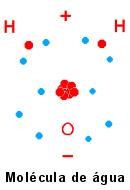
1 - ADIÇÃO, SUBTRAÇÃO, MULTIPLICAÇÃO E DIVISÃO

A CRIAÇÃO DOS NÚMEROS


Os números foram invetados pelos homens. Mas sua criação não aconteceu de repente surgiu da necessidade de contar coisas.
O homem primitivo, por exemplo, contava traçando riscos na madeira ou no osso, ou ainda, fazendo nós em uma corda.
Como erá dificil contar quantidades grandes e efetuar cálculos com pedras, nós ou riscos simples, a necessidade de efetuar cálculos com maior rapidez levou o homem a criar símbolos, para representar quantidade.
Na antiguidade, nem todos os povos usavam os mesmos símbolos. Vamos conhecer como alguns povos dessa época contavam.

A NUNERAÇÃO DOS ROMANOS

Os romanos representavam quantidades usando as próprias letras de seu alfabeto:

I - valia uma unidade
V - valia cinco unidades
X - representava dez unidades
L - indicava cinquenta unidades
C - valia cem unidades
D - representava quinhentas unidades
M - indicava mil unidades

As quantidades eram representadas colocando-se os símbolos uns ao lado dos outros, conforme a seguinte regra:

- Os símbolos iguais juntos, até três , significava soma de valores:

II = 1 + 1 = 2

XXX = 10 + 10 + 10 = 30

CCC = 100 + 100 + 100 = 300


- Dois símbolos diferentes juntos, com o número menor aparecendo antes do maior, significava subtração de valores:

IV = 5 - 1 = 4

XL = 50 - 10 = 40

XC = 100 - 10 = 90

- Dois símbolos diferentes juntos, com o maior aparecendo antes do menor, significa soma de valores:

LX = 50 + 10 = 60

CCXXX = 200 + 30 = 230

DC = 500 + 100 = 600

MMMD = 3000 + 500 = 3500


- Para indicar quantidades a partir de 4000, os romanos usavam um traço horizontal sobre as letras correspondentes à quantidade de milhares:

__
IV = 4000

_
V = 5000

_
VCCCXX = 5320

_____
XXIII = 23000

obs: Os Romanos não conheciam um símbolo para representar o número zero



A NÚMERAÇÃO DOS HINDUS


Foram os hindus que inventaram os símbolos que usamos até hoje :

0,1,2,3,4,5,6,7,8 e 9

Esses símbolos, divulgados pelos árabes, são conhecidos como algarismos indo-arábicos e com eles escrevemos todos os números.

Mais adiante vamos falar sobre o sistema de numeração que usamos. Você sabe, por exemplo, que 51 e 15 representam quantidades bem diferentes.




NÚMEROS NATURAIS

Quando contamos uma quantidade de qualquer coisa (objetos, animais,estrelas,pessoas,etc) empregamos os números 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,..........
Esses números são chamados de números naturais.
Existem infinitos números naturais os números que aparecem juntos, como na sequencia acima são chamados números consecutivos. Por exemplo 12 e 13 são consecutivos 13 é o sucessor (vem depois ) de 12 e 12 é o antecessor (vem antes) de 13

Observações:

1) todo número natural tem um sucessor (é o que vem depois)

2) todo número natural tem um antecessor (é o que vem antes), com exeção do zero

3) Um número natural e o seu sucessor são chamados números consecutivos.

PAR OU IMPAR

Um número natural é par quando termina em 0,2,4,6 ou 8
Os números pares são: 0,2,4,6,8,10,12,14,16......
Um número é ímpar quando termina em 1,3,5,7, ou 9.
Os números ímpares são: 1,3,5,7,9,11,13,15.......


EXERCICIOS

1) Determine

a) O sucessor de 199
R: 200
b) o sucessor de 7.777
R:7.778
c) o sucessor de 1.005.000
R: 1.005.001
d) o sucessor de 7.777.779
R: 7.777.780
e) o sucessor de 4.060.999
R: 4.061.000
f) o antecessor de 399
R: 398
g) o antecessor de 6.666
R: 6.665
h) o antecessor de 50.000
R: 49.999
i) o antecessor de 6.084.000
R: 6.083.999
j) o antecessor de 1.000.000
R: 999.999


2) Adicione
a) 137 com o seu sucessor
R: 137 + 138 = 275
b) 298 com o seus antecessor
R: 297 + 298 = 595

3) Pense em todos os números naturais que se escreve com dois algarismos

a) Quantos são pares?
R: 45
b) Quantos são ímpares?
R: 45






ADIÇÃO


juntando, quanto dá?

A professora de língua Portuguesa indicou aos alunos de 5° série os livros que eles deverão ler no primeiro bimestre do ano letivo, o primeiro tem 64 páginas e o segundo têm 72 páginas.
Nesses dois livros, quantas páginas, ao todo, os alunos vão ler?
Devemos contar as 72 páginas de um livro mais as 64 páginas do outro.
Partindo de 72 e contando mais 64 vemos chegar ao resultado. Essa contagem é demorada, não é? Por isso, você aprendeu a fazer esta conta:

72 + 64 = 136
ou

72 +
64
----
136


Adicionar significa somar, juntar , ajuntar, acrescentar.
No exemplo acima, os números 72 e 64 são parcelas da adição. O resultado, 136, é chamado soma.
Veja outro exemplo:

600 + 280= 880--soma
parcelas

Vamos somar os números 272 e 339 em duas ordens diferentes
calcule e compare os resultados
a) 272 + 339
b) 339 + 272

Na matemática, a operação da adição é usada quando devemos juntar duas ou mais quantidades.
Consideremos, então, as seguintes situações em que vamos empregar a operação de adição

1º EXEMPLO

Uma empresa tem 1748 pessoas trabalhando na sua fábrica e 566 pessoas trabalhando no seu escritório. Quantas pessoas trabalham, ao todo, nessa empresa?

Resolução
Para resolver esse problema, devemos fazer 1748 + 566, ou seja

1748---parcela
+566---parcela
----
2314---soma ou total (resultado da operação)

logo, podemos dizer que nessa empresa trabalham 2314 pessoas


2º EXEMPLO

Em uma escola, o início das aulas é às 7h 30min. Como cada aula tem 50 minutos de duração, a que horas termina a primeira aula?

Resolução
Para resolver esse problema, devemos fazer 7h 30min + 50 min, ou seja

7h 30 min----parcela
+ 50 min----parcela
---------
7h 80 min----soma ou total

Como 1 hora tem 60 minutos, então 80 minutos correspondem a 1h 20 min.
Então 7h 80 min = 7 h + 1h 20 min = 8 h 20 min

logo, podemos dizer que a primeira aula termina às 8 h 20 min


3º EXEMPLO

Durante o ano de 2008, uma equipe de futebol venceu 49 partidas, empatou 18 partidas e perdeu 5 partidas. Quantas partidas essa equipe disputou durante o ano de 2008?

Resolução
Para resolver o Problema, devemos calcular 49 + 18 + 5, ou seja :

49---parcelas
18---parcelas
+5---parcelas
--
72---soma ou total

Logo, podemos dizer que essa equipe disputou 72 partidas





EXERCÍCIOS

1) Calcule as somas

a) 10 + 11 = 21
b) 10 + 21 = 31
c) 10 + 31 = 41
d) 10 + 41 = 51e) 10 + 51 = 61
f) 10 + 61 = 71
g) 10 + 71 = 81
h) 10 + 81 = 91
i) 10 + 91 = 101
j) 12 + 66 = 78
l) 13 + 48 = 61
m) 67 + 89 = 156
n) 97 + 89 = 186o) 56 + 87 = 143
p) 84 + 77 = 161
q) 38 + 98 = 136
r) 69 + 73 = 142
s) 83 + 99 = 182
t) 73 + 37 = 110
u) 75 + 23 = 98
v) 37 + 67 = 104
x) 88 + 88 = 176
z) 99 + 99 = 198

2) calcule as somas

a) 110 + 100 = 210
b) 120 + 101 = 221
c) 130 + 111 = 141
d) 140 + 121 = 161
e) 150 + 131 = 181
f) 170 + 132 = 302
g) 180 + 134 = 314
h) 190 + 135 = 325
i) 200 + 136 = 336
j) 201 + 137 = 338
l) 210 + 138 = 348
m) 220 + 139 = 359
n) 230 + 140 = 370
o) 240 + 150 = 390
p) 250 + 160 = 410
q) 260 + 170 = 430
r) 270 + 180 = 450
s) 280 + 190 = 470
t) 290 + 200 = 490
u) 311 + 212 = 523
v) 548 + 645 = 1193
x) 665 + 912 = 1577
z) 987 + 789 = 1776


3) Efetue as adições

a) 1487 + 2365 = 3852
b) 6547 + 5478 = 12025
c) 4589 + 4587 = 9176
d) 3258 + 9632 = 12890
e) 7896 + 5697 = 13593
f) 5423 + 8912 = 14335
g) 7463 + 9641 = 17104
h) 2536 + 5847 = 8383
i) 7788 + 9988 = 17776
J) 1122 + 4477 = 5599
l) 7946 + 3146 = 11092
m) 4562 + 3215 = 7777
n) 1478 + 8632 = 10110
o) 8437 + 2791 = 11228
p) 2491 + 8461 = 10952
q) 6258 + 6412 = 12670
r) 5353 + 7887 = 13240
s) 3226 + 9558 = 12784
t) 1112 + 9994 = 11106
u) 6537 + 4538 = 11075
v) 2197 + 8617 = 10814
x) 1002 + 9913 = 10915
z) 9999 + 8888 = 18887




4) Efetue as adições

a) 296 + 1634 + 98 = 2028
b) 109 + 432 + 7482 = 8023
c) 48 + 16409 + 287 = 16744
d) 31 + 1487 + 641 + 109 = 2268
e) 3412 + 1246 = 4658

5) Determine a soma do número 273 com o seu sucessor
R: 547

6) Um objeto custa R$ 415.720,00. O comprador terá ainda R$ 28.912,00 de despesa de frete. Quanto o comprador vai pagar?
R: 444632

7) Ao receber o meu salário paguei R$ 437,12 de aluguel, R$ 68,14 de impostos. R$ 1.089,67 de gastos com alimentação e ainda me sobraram R$ 749,18. Quanto recebi de salário?
R: 2344,11

8) Um menino estuda 2 horas e 45 minutos pela manhã e 4 horas e 30 minutos à tarde. Quantos minutos estuda diariamente?
R: 435 min

9) Um automóvel passou pelo quilômetro 435 de uma rodovia. Ele ainda deverá percorrer 298 quilômetros até chegar ao seu destino. Quantos quilômetros da estrada vai percorrer para chegar ao destino?
R: 733

10) Em 1990 o Brasil vendeu para o exterior 283.356 veículos e, em 1991, essa venda foi de 345.760 veículos. Quantos veículos o Brasil vendeu para o exterior nesses dois anos?
R: 629.116

11) Uma empresa tem sede em São Paulo e feliais em outros estados. Na sede trabalham 316 pessoas e nas feliais 1098 pessoas. Quantas pessoas trabalham nessa empresa?
R: 1.414

12) Em um condomínio, há 675 lotes já vendidos e 1095 lotes para vender. Quantos lotes de terreno há nesse condomínio?
R: 1770

13) Uma escola funciona em dois turnos. No turno matutino há 1407 alunos e no turno vespertino há 1825 alunos. Quantos alunos estudam nessa escola?
R: 3232

14) Uma empresa produziu no primeiro trismestre 6905 peças. no segundo trimestre, a mesma empresa produziu 795 peças a mais que no primeiro trimestre. Nessas condições:

a) Quantas peças a empresa produziu no segundo trimestre?
R: 7670
b) Quantas peças a empresa produziu no semestre?
R: 14575

15) Nei comprou um aparelho de som por 635 reais e as caixas de som por 128 reais. Tendo pago 12 reais pela instalação, qual a quantia que ele gastou ?
R: 775

16) De acordo com o censo realizado em 1991, o estado da Paraíba tem 1.546.042 homens e 1.654.578 mulheres. Qual é a população da Paraíba segundo esse censo?
R: 3.200.620

18) Calcule:

a) 1705 + 395 =2100
b) 11.048 + 9.881 = 21.029
c) 4.907 + 62.103 = 67010
d) 275.103 + 94.924 = 370027
e) 545 + 2.298 + 99 = 2.942
f) 7.502 + 209.169 + 38.425 = 255.096




PROPRIEDADES DA ADIÇÃO DE NÚMEROS NATURAIS

Vamos observar a seguinte situações:

1º) consideremos os números naturais 40 e 24 e vamos determinar a sua soma ?
(R: 40 + 24 = 64)
trocando a ordem dos números, vamos determinar a sua soma
24 + 40 = 64
De acordo com as situações apresentadas, podemos escrever
40 + 24 = 24 + 40
Esse fato sempre vai ocorrer quando consideremos dois números naturais
Daí concluímos

Numa adição de dois números naturais, a ordem das parcelas não altera a soma.
Essa propriedade é chamada PROPRIEDADE COMUTATIVA DA ADIÇÃO


2º) Consideremos os números naturais 16,20 e 35 e vamos determinar a sua soma:

16 + 20 + 35
=36 + 35
=71


16 + 20 + 35
= 16 + 55=
=71

De acordo com as situações apresentadas, temos

(16 + 20) + 35 = 16 + (20 + 35)

Esse fato se repete quando consideramos três números naturais quaísquer

Então:

Numa adição de três ou mais números naturais quaisquer, podemos associar as parcelas de modo diferentes.
Essa propriedade é chamada PROPRIEDADE ASSOCIATIVA DA ADIÇÃO

3º) Consideremos os números naturais 15 e 0 e vamos determinar a sua soma, independentemente da ordem dos números:

15 + 0 = 15

0 + 15 = 15

Você nota que o número o não influi no resultado da adição. Então

Numa adição de um número natural com zero a soma é sempre igual a esse número natural.
Nessas condições, o numero zero é chamado ELEMENTO NEUTRO DA ADIÇÃO.





SUBTRAÇÃO
Na matemática, a operação da subtração é empregada quando devemos tirar uma quantidade de outrea quantidade.
veja o exemplo

O estádio do Pacaembu, na cidade de São Paulo, tem capacidade para 40.000 pessoas. È também na cidade de São Paulo que se encontra o estádio do Morumbi que tem capacidade para 138.000 pessoas.
Para se ter uma idéia do tamanho do Morumbi, se colocarmos nele 40.000 ainda sobrarão muitos lugares. Quanto sobrarão?

Dos 138.000 lugares devemos tirar os 40.000 assim

138.000 - 40.000 = 98.000

sobrarão 98.000 lugares.

Subtrair significa tirar,diminuir.

Na subtração anterior, o número 138.000 é chamado minuendo e 40.000 é o subtraendo, o resultado, 98.000, é chamado diferença ou resto.

1) calcule as subtrações

a) 47 - 31=16
b) 58 - 45=13
c) 65 - 57=8
d) 89 - 65=24
e) 97 - 21=76
f) 78 - 34=44
g) 56 - 31=25
h) 87 - 78=9
i) 98 - 78=20
j) 48 - 29=19
l) 38 - 29=9
m) 68 - 59=9
n) 56 - 37=19
o) 23 - 19=4
p) 99 - 81=18
q) 21 - 19=2
r) 23 - 22=1
s) 18 - 14=4
t) 74 - 49=25
u) 74 - 37=37
v) 74 - 52=22
x) 74 - 63=11
z) 96 - 13=83

2) Calcule as Subtrações

a) 72224-6458= (R: 65766)
b) 701-638= (R: 63)c) 131003-88043= (R: 42960)
d) 1138-909= (R: 229)
e) 80469-6458 = (R: 74011)
f) 866 - 638 = (R: 228)
g) 131012-88142= (R: 42870)
h)2238 - 909 = (R: 1329)i) 802-638 = (R: 164)

3)Dom Pedro II, imperador do Brasil, faleceu em 1891 com 66 anos de idade. Em que ano ele nasceu? R: 1825

4) Um avião Boeing 747 pode transportar 370 passageiros e um avião DC-10 pode transportar 285 passageiros. Quantos passageiros o Boeing 747 pode transportar a mais que o DC10? R: 85 passageiros

5) À vista um automóvel custa 26.454 reais. À prazo o mesmo automóvel custa 38.392 reais. A diferença entre o preço cobrado é chamado de juros. Qual é a quantia que pagará de juros? R: 11.938

6) Um avião pode transportar 295 passageiros. Em determinado vôo, o avião está transportando 209 passageiros. Quantas poltronas desse avião não estão ocupadas?
R: 86

7) Se Antonio tem 518 selos e Pedro tem 702 selos, Quantos selos Pedsro tem a mais que Antonio?
R: 184

8) Ézio tem 95 reais e quer comprar uma máquina fotográfica que dusta 130 reais. Quantos reais faltam para ele comprar a máquina?
R: 35

9)De acordo com o Censo de 1980, a população de uma cidade era de 79.412 habitantes. Feito o Censo em 1991, verificou-se que a população dessa cidade passou a ser de 94.070 habitantes. Qual foi o aumento da população dessa cidade nesse período de tempo?
R: 14.658

10)Uma industria, no final de 1991, tinha 10.635 empregados. No inicio de 1992 em virtude da crise econômica dispensou 1.880 funcionários. Com quantos funcionários a indúria ficou?
R: 8.755

11) Qual a diferença entre 10.000 e 5.995?
R: 4005

12) Quantas unidades faltam a 499 para atingir 1 inidade de milhar?
R: 501

13) Efetue:
a) 2620 - 945 = 1.675
b) 7000 - 1096 = 3904
c) 11011 - 7997 = 3014
d) 140926 - 78016 = 62910

14) Considere os números 645 e 335. Nessas condições:

a) Determine a diferença entre eles
R: 310

b) Adicione 5 unidades ao primeiro número e 5 unidades ao segundo número e calcule a difença entre os novos números que você obteve.
R: 650,340, 310






MULTIPLICAÇÃO



A multiplicação é uma adição de parcelas iguais.

veja

3+3+3+3 = 12

Podemos representar a mesma igualdade por

4 x 3 = 12 ou 4 . 3 = 12

Essa operação chama-se multiplicação e é indicada pelo sinal . ou x

Na multiplicação 4 x 3 = 12

dizemos que;

4 e 3 são os fatores
12 é o produto

1º exemplo
Um edifício de apartamentos tem 6 andares. Em cada andar a 4 apartamentos. Quantos apartamentos tem o edificio todo?

Resolução
Para resolver esse problema, podemos fazer

4 + 4 + 4 + 4 + 4 + 4 = 24

Essa mesma igualdade pode ser representada por:

6 x 4 = 24

Logo podemos dizer que o edificio tem 24 apartamentos

2° Exemplo

A fase final do torneio de voleibol da liga nacional é disputado por 4 equipes. Cada equipe pode inscrever 12 jogadores. Quantos jogadores serão inscritos para disputar a fase final desse torneio?

resolução
Para resolver esse problema podemos fazer 12 + 12 + 12 + 12 = 48

Essa mesma igualdade pode ser representada por:

4 x 12 = 48

EXERCÍCIOS

1) Calcule as multiplicações

a) 5 x 5 = 25
b) 5 x 15 = 75
c) 5 x 115 = 575
d) 5 x 25 = 125
e) 5 X 125 = 625
f) 5 x 55 = 275
g) 5 x 75 = 375
h) 5 x 375 = 1875
g) 5 x 1257 = 6285
h) 6 x 5 = 30
i) 6 x 15 = 90
j) 6 x 115 = 690
l) 6 x 25 = 150
m) 6 x 125 = 750
n) 6 x 55 = 330
o) 6 x 75 = 450
p) 6 x 375 = 2250
q) 6 x 1257 = 7542
r) 7 x 5 = 35
s) 7 x 15 = 105
t) 7 x 115 = 805
u) 7 x 25 = 175
x) 7 x 125 = 875z) 7 x 55 = 385

2) Calcule as multiplicações

a) 7 x 75 = 525
b) 7 x 375 = 2625
c) 7 x 1257 = 8799d) 8 x 5 = 40
e) 8 x 15 = 120
f) 8 x 115 = 920
g) 8 x 25 = 200
h) 8 x 125 = 1000
i) 8 x 55 = 440
j) 8 x 75 = 600
l) 8 x 375 = 3000
m) 8 x 1257 = 10056
n) 9 x 5 = 45o) 9 x 15 = 135
p) 9 x 115 = 1035
q) 9 x 25 = 225
r) 9 x 125 = 1125
s) 9 x 55 = 495
t) 9 x 75 = 675
u 9 x 375 = 3375
v) 9 x 1257 = 11313
x) 9 x 999 = 8991
z) 9 x 123 = 1107

3) Efetue as Multiplicações

a) 153 x 7 = 1071
b) 1007 x 9 = 9063
c) 509 x 62 = 31558
d) 758 x 46 = 34868
e) 445 x 93 = 41385
f) 289 x 140 = 40460
g) 1782 x 240 = 427680
h) 2008 x 405 = 813240
i) 2453 x 1002 = 2457906

4) Efetue as multiplicações

a) 28 x 0 = 0
b) 49 x 10 = 490
c) 274 x 10 = 2740
d) 158 x 100 = 15800
e) 164 x 1000 = 164000
f) 89 x 10000 = 890000

5) Considerando 1 mês = 30 dias e 1 ano = 365 dias, uma semana = 7 dias, determine:
a) quantos dias há em 15 semanas completas. (R: 105 dias)
b) Quantos dias há em 72 meses completos. (R: 2160 dias)
c) Quantos dias há em 8 anos completos. (R: 2920 dias)

6) Para uma demonstração de ginástica, um professor de Educação Fisica prepara 64 grupos de alunos. Cada grupo é formado por 25 alunos. Quantos alunos devem participar dessa demostração? R: 1600

7) Com 12 prestações mensais iguais de 325 reais posso comprar uma moto. Quanto vou pagar por essa moto? R: 3900 reais

8) Qual é o número natural que você vai obter quando multiplicar 736 por 208?
R: 153.0889) Para cobrir o piso de um barracão foram colocados 352 placas de 35 metros quadrados cada uma. Quantos metros quadrados tem o piso desse barracão?
R: 12320 metros quadrados

10) Um carro bem regulado percorre 12 quilômetros com um litro de gasolina. Se numa viagem foram consumidos 46 litro, qual a distância em quilômetos que o carro percorreu? R: 552 quilômetros
11) Em um teatro há 18 fileiras de poltronas. Em cada fileira foram colocadas 26 poltronas. Quantas poltronas há nesse teatro? R: 468 poltronas
.
12) Em uma multiplicação, os fatores são 134 e 296. Qual o produto? R: 39.664

13) Numa mercearia há 7 caixas de bombons e cada caixa contém 3 duzias de bombons. Quantos bombons há na mercearia? R: 252

14) Uma pessoa deu R$ 4.700,00 de entrada na compra de um objeto e pagou mais 6 prestações de R$ 2.300,00. Quanto custou o objeto? R: 18.500

16) Um motorista percorreu 749 km em 6 dias. Nos cinco primeiros dias andou 132 km por dia. Quanto percorreu no 6º dia ? R: 89

17) Calcule:

a) 19x6=114
b) 46x12=552
c) 321x11=3531
d) 329x25=8225
e) 1246x24=29904
f) 67632x101=6830832

18) Calcule as contas:

a) 18x5x2=180
b) 5x2x24=240
c) 2x5x44=440
d) 37x2x5=370
e) 12x4x5=240f) 4x5x15=300

19)


PROPRIEDADES ESTRUTURAIS DA MULTIPLICAÇÃO

1) FECHAMENTO
O priduto de dois números naturais é um número natural
5 x 3 = 15

2) COMUTATIVA
A ordem dos fatores não altera o produto.

2 x 7 = 14
7 x 2 = 14

assim: 2 x 7 = 7 x 2

3) ELEMENTO NEUTRO
O número 1´na multiplicação é um número neutro

5 x 1 = 5
1 x 5 = 5

4) ASSOCIATIVA
A multiplicação de três números naturais pode ser feita associando-se os os dois primeiros ou os dois ultimos fatores

(3 x 4 ) x 5 = 12 x 5 = 60
3 x ( 4 x 5 ) = 3 x 20 = 60

5) DISTRIBUTIVA DA MULTIPLICAÇÃO EM RELAÇÃO A ADIÇÃO
Na multiplicação de uma soma por um número natural, multiplica-se cada um dos termos por esse número .

veja:

1) 2 x (5+3) = 2 x 8 = 16

2) 2 x 5 + 2 x 3 = 10 + 6 = 16




DIVISÃO EXATA



Consideremos dois números naturais, dados numa certa ordem, 10 é o primeiro deles e 2 é o segundo .
Por meio deles determina-se um terceiro número natural que, multiplicado pelo segundo dá como resultado o primeiro. Essa operação chama-se divisão e é indicada pelo sinal :

Assim,

10:2 = 5 porque 5x2 = 10

Na divisão 10:2=5

dizemos que
10 é o dividendo
2 é o divisor
5 é o resultado ou quociente

EXEMPLO

Um cólegio levou 72 alunos numa excursão ao jardim zoológico e para isso repartiu igualmente os alunos em 4 ônibus. Quantos alunos o colégio colocou em cada ônibus?

Para resolver esse problema, devemos fazer uma divisão 72 : 4 = 18 , sendo assim cada ônibus tinha 18 alunos.


EXERCÍCIOS

1) Calcule as divisões
a)20:5=4
b)16:8=2c)12:1=12
d)48:8=6
e)37:37=1
f)56:14=4

2)Observe a igualdade 56:7=8 e responda:

a)Qual é o nome da operação?
R: divisão
b)Como se chama o número 56?
R: dividendo
c)Como se chama o número 7?
R: divisor
d)como se chama o número 8?
R: Quociente ou resultado

3)Efetue as divisões

a)492:4=123
b)891:9=99
c)4416:6=736
d)2397:17=141
e)1584:99=16
f)1442:14=103
g)21000:15=1400
h)7650:102=75
i)11376:237=48

4) Responda

a)Qual é a metade de 784?
R: 392
b)Qual é a terça parte de 144?
R: 48
c)Qual é a quinta parte de 1800?
R: 360
d)Qual é a décima parte de 3500?
R: 350

5)Em um teatro há 126 poltronas distribuídas igualmente em 9 fileiras. Quantas poltronas foram colocadas em cada fileira?
R: 14 poltronas

6)Quantos garrafões de 5 litros são necessários para engarrafar 315 litros de vinho?
R: 63 garrafões

7)Uma pessoa ganha R$ 23,00 por hora de trabalho. Quanto tempo deverá trabalhar para receber R$ 391,00?
R: 17 horas

8)Uma torneira despeja 75 litros de água por hora. Quanto tempo levará para encher uma caixa de 3150 litros ?
R: 42 horas9) Numa pista de atlestismo uma volta tem 400 metros. Numa corrida de 10.000 metros, quantas voltas o atleta tem de dar nessa pista?
R: 25 voltas

10) Um livro tem 216 páginas. Quero terminar a leitura desse livro em 18 dias, lendo o mesmo número de páginas todos os dias. Quantas páginas preciso ler por dia?
R: 12 paginas

11)Quantos grupos de 18 alunos podem ser formados com 666 alunos?
R: 37 grupos

12)Uma tonelada de cana de açucar produz aproximadamente 85 litros de álcool. Quantas toneladas de cana são necessárias para produzir 6970 litros de álcool?
R: 82 toneladas




DIVISÃO NÃO EXATA


Nem sempre é possivel realizar a divisão exata em N

considerando este exemplo

7 : 2 = 3 sobra 1 que chamamos de resto

Numa divisão, o resto é sempre menor que o divisor

Exemplo

Uma industria produziu 183 peças e quer colocá-las em 12 caixas, de modo que todas as caixas tenham o mesmo número de peças. Quantas peças serão colocadas em cada caixa?

resolução
Para resolver esse problema devemos fazer 183 : 12, tendo como resultado 15 e resto 3.
Como o resto é 3, dizemos que esta é uma divisão com resto ou uma divisão não exata.
Logo na caixa serão colocadas 15 peças, sobrando ainda 3 peças.

EXERCÍCIOS

1) Determine o quociente e o resto das seguintes divisões:
a 79:8=9 resto=7
b)49:8=6 resto=1
c)57:8=7 resto=1
d)181:15=12 resto=1
e)3214:10=321 resto=4
f)825:18=45 resto=15
g)4937:32=154 resto=9
h)7902:12=658 resto=6
i)1545:114=13 resto=63