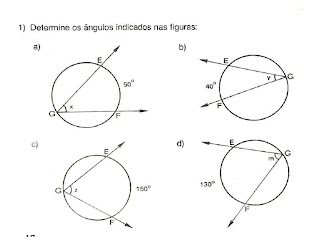
CIRCUNFERÊNCIA
Circunferência é o conjunto de pontos de um plano, equidistantes de um ponto do plano chamado centro.
Qualquer segmento com uma extremidade no centro e a outra em um ponto da circunferência é chamado de raio
CORDA E DIÂMETRO
Corda é o segmento cujas extremidades pertencem à circunferência
Diâmetro é a corda que passa pelo centro da circunferência.
Observe que a medida do diâmetro é o dobro da medida do raio, ou seja:
D = 2r
CIRCULO
Observe as figuras e seus respectivos nomes :
Convém destacar que:
- todo ponto da circunferencia pertence ao círculo.
- Existem pontos do círculo que não pertencem à circunferência
- O centro, o raio e o diâmetro da circunferência são também centro, centro, raio e diametro do círculo.
EXERCÍCIOS
3) Determine:
a) o diâmetro de uma ciordunferência cujo raio mede 4,5 cm.
b) O raio de uma circunferência cujo diâmetro mede 17 cm
c) o diâmetro de uma circunferência cujo raio é igual a x.
5) O raio de uma circunferência é dado por r = 2x -6. Se o diâmetro mede 20 cm, calcule x.
POSIÇÕES RELATIVAS DE UMA RETA E UMA CIRCUNFERÊNCIA
Uma reta r e uma circunferência C podem ocupar as seguintes possições:
POSIÇÕES RELATICAS DE DUAS CIRCUNFERÊNCIAS
Duas circunferências distintas podem ser:
EXERCÍCIOS
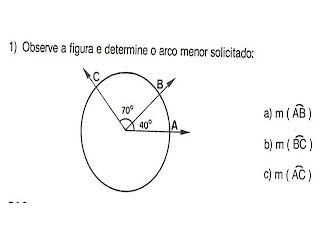
1) Observe a figura e classifique:
2) Observe a figura e responda:
ARCOS
ÂNGULO CENTRAL
EXERCÍCIOS
ÂNGULO INSCRITO
exemplos
EXERCÍCIOS
CVCVCVCV
MONDAY, NOVEMBER 28, 2011
15 - POLÍGNOS CONVEXOS
POLÍGNOS
Plignos é um conjunto de segmentos consecutivos não colíneares no qual os extremos do primeiro e do último coincidem.
Assim como já vimos para os quadriláteros, dizemos que um polígno é convexo quando qualquer segmento com extremidades no polígno está contido nele.
ELEMENTOS DE UM POLÍGNO
NOMES DOS POLÍGONOS
Segundo o número de lados, os polígonos recebem nomes especiais:
O número de lados de um polígono é igual ao número de vértices.
EXERCÍCIOS
1) Quais são os poligonos convexos?
2) Responda:
a) Quantos lados tem um hexágono?
b) Quantos lados tem um undecágono?
c) Quantos lados tem um polígono de 15 vértices ?
d) Quantos vértices tem um polígono de 9 lados?
3) Como se chama um polígono de:
a) 5 lados?
b) 12 lados?
c) 7 vértices?
d) 20 vértices?
SOMA DOS ÂNGULOS IN TERNOS DE UM POLIGONO CONVEXO
Ao traçar as diagonais qywe partem de um mesmo vértice de um polígono, nós o dividimos em triângulos, cujo número de triângulos é sempre o número de lados menos dois.
veja:
Um polígono de n lados será dividido em (n - 2) triângulso. logo para obter a soma de seus ângulos , basta multiplicar o número de triângulos por 180º ou seja:
Exemplos:
Calcular a soma dos ângulos internos so octógono (n = 8)
EXERCÍCIOS
1) Calcule a soma dos ângulos internos dos seguintes polígonos :
a) pentágono
b) hexágono
c) eneagono
d) decagono
e) pentadecagono
f) icoságono
2) Qual a soma dos ângulos inbternos de um polígono convexo de 7 vértices?
3) A soma dos ângulos internos de um polígono convexo é 900º Qual é o poligono?
4) A soma dos ângulos internos de um polígono convexo é 3240º . Qual é o polígono?
5) Calcule x
EXERCÍCIOS
1) Qual é a medida de cada ângulo interno de um triângulo equilátero?
2) Calcule a medida do ângulo interno de cada polígono regular:
a) pentágono
b) hexagono
c) octógono
d) dodecágono
DIAGONAL DE UM POLÍGONO
Diagonal de um polígono é um segmento cujas extremidades são vertices não consecutivos do polígono.
NÚMERO DE DIAGONAIS DE UM POLÍGONO
Exemplo
Calcule o número de diagonais de um octógono
EXERCÍCIOS
1) Calcule o número de diagonasis dos seguintes polígonos
a) hexágono
b) heptágono
c) eneágono
d) decágono
e) dodecágono
f) icoságono
2) Quantas diagonais tem um poligono de 25 lados?
3) Qual é o poligono cujo número de lados é igual ao número de diagonasi?
4) Qual é o poligono cujo o número de diagonais é o dobro do número de lados ?
5) A soma dos ângulos internos de um poligono convexo é 1080º Calcule o número de diagonais desse poligono.
TUESDAY, NOVEMBER 08, 2011
03 - TERMOS SEMELHANTES
TERMOS SEMELHANTES
Dois ou mais termos são semelhantes quando têm a mesma parte literal.
Exemplos:
a) 5m e -7 m são termos semelhantes
b) 2xy³ e 9y³x São termos semelhantes
Obs: veja que não importa a ordem dos fatores literais
Não são semelhantes os termos :
a) 4x e 7x²
b) 3xy² e 4x²y
Obs : que os expoentes de x são diferentes
EXERCÍCIOS
1) Quais os pares de termos semelhantes?
a) 7a e 4a (X)
b) 2x² e -6x² (X)
c) 4y e 5y²
d) 8xy e –xy (X)
e) -5a e -4ab
f) 4ab e 5/8 ab (X)
g) 8xy e 5yx (X)
h) 4x²y e –xy
i) xy²e 2x²y
j) 3acb e abc (X)
k) x/2 e 7x (X)
2) Considere:
a) 3ab²
b) -6x²
c) 8a²b
d) 7a²b
e) 5x
f) 9x²
g) -4x²
h) -2ab²
i) -ab²
j) 3ax
Forme o conjunto de termos semelhantes
REDUÇÃO DE TERMOS SEMELHANTES
Quando numa mesma expressão, tivermos dois ou mais termos semelhantes, podemos reduzi-los todos a um único termo, usando a propriedade distibutiva
Exemplos:
1) 5x + 3x – 2x = 6x
2) 7xy – xy + 5xy = 11xy
Conclusão: somamos os coeficientes e conservamos a parte literal
EXERCÍCIOS
1) Reduza os termos semelhantes:
a) 8a + 2a = (R: 10a)
b) 7x – 5x = (R: 2x)
c) 2y²- 9y² = ( R: -7y²)
d) 4a² - a² = (R: 3a²)
e) 4y – 6y = (R: -2y)
f) -3m²+ 8m² = (R: 5m²)
g) 6xy²- 8y²x = (R: -2xy²)
h) 5a – 5a = (R: 0)
2) Reduza os termos semelhantes:
a) 8x + 1x/2 = (R: 17x/2)
b) 3a – 2a/3 = (R: 7a/3)
c) 1x/2 + 1x/3 = (R: 5x/6)
d) 2 x²/3 - 1 x²/2 = (R: 1 x² /6)
e) 1y/2 – 2y/5 = (R: 1y/10)
f) 2x + 1x/2 -3x/4 = (R: 7x/4)
3) reduza os termos semelhantes:
a) 7x -5x + 3x = (R: 5x)
b) 2y – y – 10y = (R: -9y)
c) 4a + a – 7a = (R: -2a)
d) x²+ x² - 2x² = (R: 0)
e) ab – ab + 5ab = (R: 5ab)
f) 4x³- x³ + 2x³ = (R: 5x³)
g) 10x – 13x –x = (R: -4x)
h) 8x – 10x + 4x = (R: 2x)
Há casos em que numa expressão há termos diferentes e termos semelhantes entre si. Observe que a redução só pode ser feita com termos semelhantes
Exemplo 1
7x + 8y -2x – 5y
7x – 2x + 8y – 5y
5x + 3y
Exemplo 2
4a³ + 5a² + 7a – 2a²+ a³- 9a + 6
4a² + a³+ 5a² - 2a² + 7a – 9a + 6
5a³ + 3a² - 2a + 6
Exercícios
1) Reduza os termos semelhantes
a) 6a + 3a -7
b) 4a – 5 – 6a
c) 5x²+ 3x² -4
d) X – 8 + x
e) 4m – 6m -1
f) 4a – 3 +8
g) x²- 5x + 2x²
h) 4a – 2m – a
i) Y + 1 – 3y
j) X + 3xy + x
2) Reduza os termos semelhantes:
a) 1/2x – 1/3y + x
b) 4a – 1/2a + 5 – 1/3
c) 1/2a – 3a²+ a + 3a
d) 4y – 3/5y +1/2 + 1
e) 2m + 3 + m/2 – 1/2
ELIMINAÇÃO DE PARENTESES, COLCHETES E CHAVES
Vamos lembrar que:
Ao eliminar parênteses precedidos pelo sinal de (+), não toque o sinais dos termos incluídos nos parênteses.
Exemplos:
2x + (5x -3)
2x + 5x – 3
7x – 3
2) Ao eliminarmos parênteses precedidos pelo sinal negativo (-) troque os sinais incluídos nos parênteses.
Exemplo:
7x – (4x – 5)
7x -4x + 5
3x + 5
Para eliminação de colchetes e chaves são validas as regras acima.
Exemplos
1) 5x + (3x – 4) - (2x – 9)
5x + 3x – 4 – 2x + 9
5x + 3x – 2x – 4 + 9
6x + 5
2) 8x – [ -2x + (10 + 3x – 7)]
8x – [ -2x + 10 +3x – 7]
8x +2x – 10 – 3x + 7
8x + 2x -3x - 10 +7
7x – 3
3) 2a² + { 3a – [ 6a – (3a² + a)]}
2a² + { 3a – [ 6a – 3a² - a]}
2a² + { 3a – 6a + 3a² + a}
2a² + 3a – 6a + 3a² + a
2a² + 3a² + 3a – 6a +a
5 a² -2ª
EXERCÍCIOS
1) Reduza os termos semelhantes nas seguintes expressões algébricas:
a) 6x + (2x – 4) – 2 = (R: 8x -6)
b) 7y -8 – (5y – 3) = (R: 2y -5)
c) 4x – ( -3X + 9 – 2X) = ( R: 9x – 9)
d) 3x – (-2x + 5) – 8x + 9 = (R: -3x + 4)
e) 4x – 3 + (2x + 1) = (R: 6x -2)
f) (x + y) – (x + 2y) = (R: -y)
g) ( 3x – 2y) + (7x + y) = (R: 10x – 19)
h) –(8a + 4 – ( 3a + 2) = (R: -11a -6)
2) Reduza os termos semelhantes nas seguintes expressões algébricas
a) 5a + (3a -2) – (10a – 8) = (R: -2a + 6)
b) 6x + (5x -7) – (20 + 3x ) = (R: 8x -27)
c) (x + y + z) + x – (3y + z) = ( R: 2x – 2y)
d) (m + 2n ) – ( r – 2n) – ( n+ r) = (R: m + 3n – 2r)
e) – (6y + 4x ) + ( 3y – 4x ) – (-2x + 3y) = (R: -6y – 6x)
3) Reduza os termos semelhantes nas seguintes expressões algébricas
a) 6x² - [ 4x² + (3x – 5) + x] = (R: 2x²- 4x + 5)
b) 3X + { 2Y – [ 5X – (Y + X)]} = (R: -1x + 3y)
c) – 3x + [ x² - ( 4x² - x ) + 5x] = (R: 0 )
d) Xy – [ 2x + (3xy – 4x ) + 7x] = (R: 2xy – 5x)
e) 8a – [ ( a + 2m) – ( 3a – 3m)] = (R: 10a – 5m)
f) a– (b – c) + [ 2a + (3b + c)] = (R: 3a + 2b + 2c)
g) –[x + (7 – x) – (5 + 2x)] = (R: -2x -2)
h) { 9x – [ 4x – (x – y)- 5y] + y} = (R: 6x + 5y)
i) (3a + 2m ) – [ ( a – 2m) – (6a + 2m)] = (R: 8a + 6m)
j) 7x³- { 3x² - x – [ 2x – { 5x³ - 6x² ) – 4x ]} = (R: 2x³ + 3x²- 1x)
k) 2y – { 3y + [4y – (y – 2x) + 3x ] – 4x } + 2x = (R: 11y – 4x)
l) 8y + { 4y – [ 6x – y- (4x – 3y) – y ] – 2x } = (R: 6x + 4y)
m) 4x – { 3x + [ 4x – 3y – (6x – 5y ) – 3x ] – 6y}
n) 3x – { 3x – [3x – (3x –y) – y ] – y} - y
4) Reduza os termos semelhantes das expressões algébricas
a) -2n – (n – 8) + 1 = (R: -3n + 9)
b) 5 – ( 2a – 5 ) + a = (R: -a + 10)
c) 3x + ( -4 – 6x) + 9 = (R: -3x + 5)
d) 8y – 8 – ( -3y + 5) = (R: 11y – 13)
e) a – [ n + ( a + 3) ] = (R: -n -3)
f) 5 + [ x – (3 – x)] = (R: 2x + 2)
g) x² - [ x – (5 - x²)] = (R: -x + 5)
h) 5x – y – [ x – ( x – y)] = (R: 5x – 2y)
5) Reduza os termos semelhantes das expressões algébricas
a) 2x + ( 2x + y) – (3x – y) + 9x = (R: 10x + 2y)
b) 5a – { 5a – [ 5a – (5a – m) – m] – m } – m = (R: 0)
c) – { 7a – m – [ 4m – (n – m + 3a) – 4a] + n } = (R : 14a + 6m – 2n)
d) 5xy – [ - (2xy + 5x) + [ 3Y – (-XY + X + 3XY)]} = (R: 9X + 6X -3Y)
e) – {x – 2y + y – [ 3x + 5xy + 6y – (x –y) + 8 ]} = (R: x + 8y + 5xy + 8)
jmpgeo.blogspot.com.br