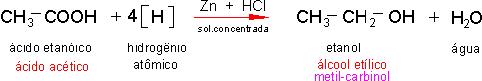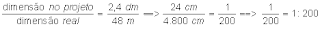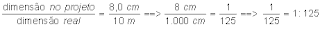É o período constituído de duas ou mais orações, sabendo-se que cada oração é, obrigatoriamente, estruturada em torno de um verbo.
"Traziam / não sei / que fluido misterioso e enérgico, uma força / que arrastava para dentro,/ como a vaga / que se retira da praia, nos dias de ressaca. (M. Assis).
I - ORAÇÕES SUBORDINADAS
São orações dependentes sintaticamente de outra. Exercem uma função sintática correspondente ao substantivo, adjetivo ou advérbio.
Exemplo:
Os credores internacionais esperavam / que o Brasil suspendesse o pagamento dos juros.
Nesse exemplo, a segunda oração está subordinada à primeira, pois exerce função sintática de objeto direto do verbo esperar.
São aquelas que exercem função sintática própria de um substantivo, a saber: sujeito, objeto direto, objeto indireto, complemento nominal, predicativo do sujeito, aposto ou agente da passiva. Assim temos:
a) Subjetiva
Função de sujeito em relação ao verbo da principal.
Exemplos:
É importante / que tenhamos o equilíbrio da balança comercial.
Ainda se espera / que o governo mude as normas do imposto de renda.
Ainda era esperado / que a equipe palmeirense se reabilitasse.
Consta / que haverá mudanças no ministério, caso o presidente seja reeleito.
b) Objetiva direta
Função de objeto direto em relação ao verbo da principal.
Exemplo:
Os contribuintes esperam / que o governo altere as normas do imposto de renda.
c) Objetiva indireta
Função de objeto indireto em relação ao verbo da principal.
Exemplo:
O país necessita / de que se faça uma melhor distribuição de renda.
d) Completiva nominal
Função sintática de complemento nominal em relação a um substantivo, adjetivo ou advérbio da principa
Exemplos:
O país tem necessidade / de que se faça uma reforma social.
O governador era contrário / a que mudassem as regras do jogo.
Percebia-se que agia favoravelmente / a que mudassem as regras do jogo.
e) Predicativa
Função de predicativo do sujeito em relação à principal.
Exemplo:
O medo dos empresários era / que sobreviesse uma violenta recessão.
f) Apositiva
Função de aposto em relação a um termo da principal.
Exemplo:
O receio dos jogadores era esse: / que o técnico não os ouvisse.
g) Agente da passiva
Função de agente da passiva em relação à principal.
Exemplo:
O assunto era explicado / por quem o entendia profundamente.
São aquelas que exercem função sintática própria de um adjetivo:
a) Restritivas
Restringem, limitam o sentido de um termo da oração principal. Não são isoladas por vírgulas.
Exemplo:
A doença que surgiu nestes últimos anos pode matar muita gente.
b) Explicativas
Explicam, generalizam o sentido de um termo da oração principal. São isoladas por vírgulas.
Exemplo:
As doenças, que são um flagelo da humanidade, já mataram muita gente.
Observação:
As orações subordinadas adjetivas são introduzidas por pronomes relativos: que, quem, o qual, a qual, cujo, onde, como, quando etc.
Os pronomes relativos exercem funções sintáticas, a saber:
a) Sujeito
Exemplo:
Os trabalhadores que fizeram greve exigiam aumento salarial.
(= Os trabalhadores fizeram greve.)
b) Objeto direto
Exemplo:
As reivindicações que os trabalhadores faziam preocupavam os empresários.
(= Os trabalhadores faziam as reivindicações.)
c) Objeto indireto
Exemplo:
O aumento de que todos necessitavam proveria o sustento da casa.
(= Todos necessitavam do aumento.)
d) Complemento nomina
Exemplo:
O aumento de que todos tinham necessidade proveria o sustento da casa.
(= Todos tinham necessidade do aumento.)
e) Predicativo do sujeito
Exemplo:
O grande mestre que ele sempre foi agradava a todos.
(= Ele sempre foi o grande mestre.)
f) Adjunto adnominal
Exemplo:
Os peregrinos de cujas contribuições a paróquia dependia retornaram à sua cidade.
(= A paróquia dependia de suas contribuições.)
g) Adjunto adverbial
Exemplo:
Observem o jeitinho como ela se requebra.
(= Ela se requebra com jeitinho.)
São aquelas que exercem função sintática própria de advérbio, ou seja, adjunto adverbial em relação à principal.
a) Causal
Exemplo:
Todos se opuseram a ele, porque não concordavam com suas idéias.
b) Condicional
Exemplo:
Se houvesse opiniões contrárias, o acordo seria desfeito.
c) Temporal
Exemplo:
Assim que chegou a casa, resolveu os problemas.
d) Proporcional
Exemplo:
Quanto mais obstáculos surgiam, mais ele se superava.
e) Final
Exemplo:
O pai sempre trabalhou para que os filhos estudassem.
f) Conformativa
Exemplo:
Os jogadores procederam segundo o técnico lhes ordenara.
g) Consecutiva
Exemplo:
Suas dívidas eram tantas que vivia nervoso.
h) Concessiva
Exemplo:
Embora enfrentasse dificuldades, procurava manter a calma.
i) Comparativa
Exemplo:
Ele sempre se comportou tal qual um cavalheiro.
II - ORAÇÕES COORDENADAS
As orações coordenadas são independentes sintaticamente. Não exercem nenhuma função sintática em relação a outra dentro do período.
Quando não são introduzidas por conjunções (conectivos), são classificadas como assindéticas.
Exemplo:
"No alto da figueira estava, / no alto da figueira fiquei." (J. C. de Carvalho)
Se introduzidas por conjunções (conectivo), classificam-se como sindéticas, recebendo o nome da conjunção que as introduzem, assim:
a) aditivas (e, nem, mas também...)
Exemplo:
O ministro não pediu demissão e manteve sua posição anterior.
b) adversativa (mas, porém, todavia, contudo, entretanto)
Exemplo:
O ministro pediu demissão, mas o presidente não a aceitou.
c) explicativas (que, porque, e a palavra pois antes do verbo)
Exemplo:
Peçam a demissão dos seus assessores, pois eles pouco fazem para o bem do povo.
d) conclusivas (logo, portanto, por conseguinte, por isso, de modo que e a palavra pois após o verbo)
Exemplo:
Os assessores pouco fazem pelo povo; devem, pois, deixar seus cargos.
e) alternativas (ou, ou ... ou, ora ... ora, quer ... quer, seja ... seja, já ... já, talvez ... talvez)
Exemplo:
O Congresso deve ser soberano, ou perderá a legitimidade.
III - ORAÇÕES REDUZIDAS
Não são introduzidas por conjunção e possuem verbo em uma das formas nominais (infinitivo, particípio ou gerúndio).
a) Infinitivo (pessoal ou impessoal)
Exemplos:
Todos sabiam ser impossível a manutenção da política econômica.
O.S.S.Objetiva Direta reduzida de infinitivo.
Seria bom manteres a calma nesse momento.
O.S.S. Subjetiva reduzida de infinitivo.
b) Gerúndio
Exemplos:
Entrando na sala de aula, foi recebido com frieza.
O.S. Ad. Temporal reduzida de gerúndio.
Vencendo seus adversários futuros, o clube ganhará o campeonato.
O.S. Adv. Condicional reduzida de gerúndio.
c) Particípio
Exemplos:
Realizado o congresso internacional, percebeu-se a gravidade da moléstia.
O.S. Ad. Temporal reduzida de particípio.
Encontrado o autor dos assaltos, a população ficará aliviada.
O.S. Condicional reduzida de particípio.
Entristecido com a campanha do seu clube, não mais discutia futebol.
O.S. Adv. Causal reduzida de particípio.
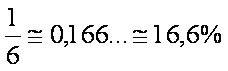
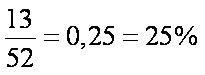



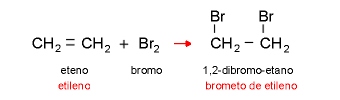
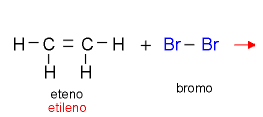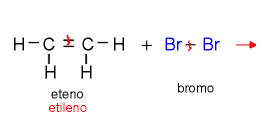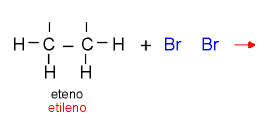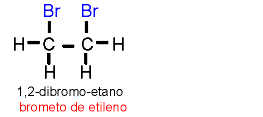
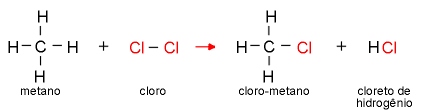
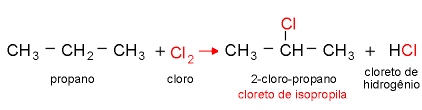 03 - Reação de eliminação: quando átomos ou radicais são eliminados da molécula orgânica.
03 - Reação de eliminação: quando átomos ou radicais são eliminados da molécula orgânica. 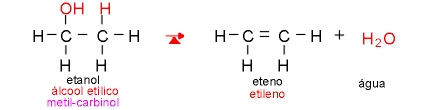 Regra de Saytzeff: Nas reações de eliminação, o hidrogênio preso ao carbono menos hidrogenado é mais facilmente eliminado.
Regra de Saytzeff: Nas reações de eliminação, o hidrogênio preso ao carbono menos hidrogenado é mais facilmente eliminado. 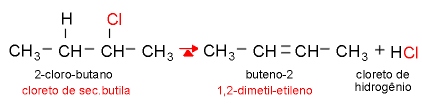


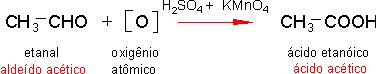

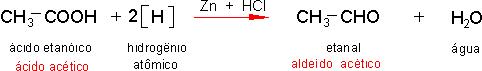
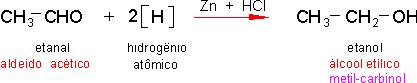
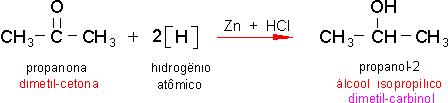 5.4 - Redução total de ácido orgânico.
5.4 - Redução total de ácido orgânico.