Como foi visto na Matemática Básica, as coordenadas polares são usadas para representar pontos de um plano.
Para definir um sistema de coordenadas polares, consideramos um ponto O do plano (chamado origem ou pólo) e uma semi-reta orientada com extremidade O ( o eixo polar). Dado um ponto P ¹O do plano tomamos,
 q , uma ângulo formado pelo eixo polar e OP, tendo origem no eixo polar, positivo se orientado no sentido anti-horário e negativo se no sentido horário. |  |
| r, a distância de P a O | |
| r e q são coordenadas polares de P e representamos P = (r, q ) |
Dado um ponto qualquer do plano, as suas coordenadas polares não são únicas.
Exemplo 1: Representar graficamente os pontos de coordenadas polares
Como estes ângulos são côngruos temos P1 = P2 = P3
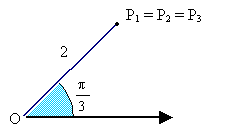
As coordenadas do pólo são (0, q ) para todo q Î R .
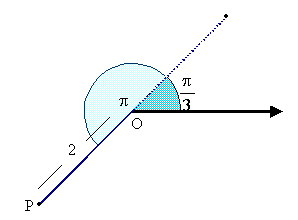
Tomamos também valores negativos para a coordenada r. Se r é negativo, o ponto de coordenadas polares (r, q ) é tal que (-r, q + p ) são também coordenadas deste ponto
Exemplo 2: Representar graficamente o ponto de coordenadas polares
Exemplo 2: Representar graficamente o ponto de coordenadas polares
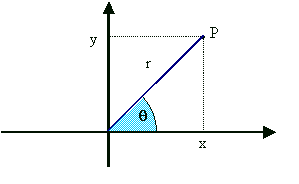
Suponhamos neste mesmo plano um par de eixos cartesianos XOY de modo que o semi-eixo OX positivo coincida com o eixo polar.
Se P é um ponto qualquer do plano de coordenadas polares (r, q ) e coordenadas cartesianas (x ,y) então
Se P é um ponto qualquer do plano de coordenadas polares (r, q ) e coordenadas cartesianas (x ,y) então
x = r.cos(q )
| y = r.sen(q ) | x2 + y2 = r2 |
Exemplo 3: Consideremos as curvas a seguir e suas equações em coordenadas polares
3.1) O círculo da raio ro e centro na origem tem equação polar r = ro
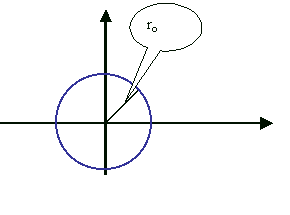
3.2) A reta que passa pela origem e faz um ângulo q o com o sentido positivo do eixo OX tem equação polar q = q o
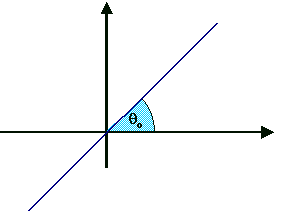
| A área de um setor circular de raio r e ângulo central q é igual a |  |
 |
Proposição 1: Seja a equação polar de uma curva dada pela função contínua r = r (q ) para a £ q £ b tal que b - a £ 2p e r ³ 0. A área da região do plano limitada pelas retas de equações polares q = a e q = b e a curva r = r(q ) é igual a.
 |  |
Para todo q tal que a £ q £ b , seja A(q ) a área como indicada na figura abaixo.
| Vamos calcular |  |
 |  |
Para D q > 0 , tomando-se no intervalo [ q , q + D q ], rM e rm o maior e o menor raio, as áreas dos setores circulares com ângulo central D q e esses raios são
 |  |
 | |
| Para D q < 0 segue de modo análogo. | |
| Pelo teorema fundamental do cálculo | |
 |
| Exemplo 4: Calcular a área limitada pela cardióide r (q ) = a.(1 – cos(q )) |  |
 | |
 | |
 | |
 |
Observação 1: São equações de cardióides:
r (q ) = a.(1 ± cos(q )) e r (q ) = a.(1 ± sen(q ))
| Exemplo 5: Calcular a área limitada pelas pétalas da rosácea r = a.sen(2q ), a > 0 |  |
| Trata-se de uma rosácea de 4 pétalas. Devido a simetria das pétalas, basta calcular a área de uma delas e multiplicar por 4. | |
 | |
 | |
 |
Observação 2: São equações de rosáceas:
r = a.cos(nq ) e r = a. sen(nq ), para n =1, 2, 3..., que possuem
- 2n pétalas , se n é par
- n pétalas se n é ímpar
| Exemplo 6: Calcular a área limitada pela lemniscata r2 = 4.cos(2q ). |  |
Como q deve ser tal que cos(2q ) >0, então, na 1a volta, | |
Devido a simetria dos semi-laços, basta cal cular a área de um deles e multiplicar por 4.  |  |
Observação 3: São equações de lemniscatas:
r2 = a.cos(2q ) e r2 = a. sen(2q )
| Exemplo 7: Calcular a área entre a 1a e a 2a volta da espiral (exponencial) r = eq , com 0 £ q . |  |
 | |
 | |
 |
Exemplo 8: Esboce a limaçon (com laço) de equação polar r = a.(1 – 2sen(q )) e determine uma expressão em integrais que represente a área da região do plano que se encontra no interior da curva e fora do laço. |  |
 |  |
Observação 4: São equações de limaçons:
r = a ± b.cos(q ) e r = a ± b.sen(q ) que possuem laço se a < b
| Exemplo 9: Determine uma expressão em integrais que represente a área da região do plano sombreada na figura ao lado onde temos o arco da espiral de Arquimedes de equação polar r = q ; -p £ q £ p . |  |
 | |
| Exemplo 10: Determine uma expressão em integrais que represente a área da região do plano interior a ambas as curvas de equações polares r =1 + cos( q ) e r = 3cos( q ) |  |
| r =1 + cos( q ) é equação de uma cardióide e r = 3cos( q ) é equação de um círculo. | |
| Obtendo a interseção das duas curvas : 3cos( q ) = 1 + cos( q ) Þ cos( q ) = 1/2 Þ q = ± p /3 + 2kp | |
 | |
fonte :http://www.mat.ufba.br/
