quarta-feira, 4 de dezembro de 2019
Equação geral dos gases
Professor de Matemática no Colégio Estadual Dinah Gonçalves
E Biologia na rede privada de Salvador-Bahia
Professor Antonio Carlos carneiro Barroso
email accbarroso@hotmail.com
Blog HTTP://ensinodematemtica.blogspot.com e HTTP://accbarroso60.wordpress.com
http://accbarrosogestar.blogspot.com.br
http://accbarrosogestar.blogspot.com.br
Extraído de http://www.alunosonline.com.br
Equação geral dos gases
Domiciano Correa Marques da Silva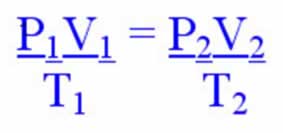
Equação geral dos gases
Nos experimentos realizados por Robert Boyle, pôde-se verificar que havia uma relação de proporção entre volume e pressão de um gás, quando a temperatura era mantida constante. Essa transformação recebeu o nome de transformação isotérmica.
Uma transformação é dita isotérmica quando a temperatura permanece constante. Nesse caso, a pressão varia de forma inversamente proporcional ao volume ocupado pelo gás.
A expressão que representa uma transformação isotérmica é conhecida como lei de Boyle-Mariotte e é representada pela seguinte equação:
p1V1 = p2V2
Onde: p1 é a pressão inicial, p2 é a pressão final, V1 volume inicial e V2 volume final.
Já o cientista Jaques Charles verificou a relação de proporção entre o volume e a temperatura de um gás quando a pressão era mantida constante.
Uma transformação é dita isobárica quando a pressão permanece constante. Nesse caso, o volume varia de forma diretamente proporcional à temperatura. A expressão para representar a transformação isobárica ficou conhecida como lei de Charles, e é representada pela equação:
V1 = V2
T1 T2
Onde: V1 volume inicial, V2 volume final, T1 temperatura inicial e T2 temperatura final.
O cientista Charles investigou também a relação existente entre a pressão e a temperatura quando o volume era mantido constante. Essa transformação é denominada isométrica, isocórica ou isovolumétrica.
Então, uma transformação é dita isovolumétrica quando o volume permanece constante, e a pressão varia proporcionalmente à temperatura. A equação que representa a lei de Charles para transformação isovolumétrica é:
p1 = p2
T1 T2
Onde: p1 é a pressão inicial, p2 é a pressão final, T1 temperatura inicial e T2 temperatura final.
Para uma transformação em que variam a pressão, o volume e a temperatura, ao mesmo tempo, temos a seguinte equação:
p1.V1 = p2.V2
T1 T2
Teorema de D’Alembert
Colégio Estadual Dinah Gonçalves
email
accbarroso@hotmail.com
matemática, os teoremas, as fórmulas, os postulados sempre recebem o nome de seus inventores e D’Alembert foi um desses, matemático e físico, foi um dos oficiais na revolução Francesa responsável pelas publicações solenes, anunciava a guerra e plocamava a paz.
Além disso, vários teoremas, tanto na física como na matemática, levaram o seu nome, na matemática podemos destacar no estudo dos polinômios o Teorema de D’Alembert, que diz:
Todo polinômio P(x) quando dividido por um binômio do tipo x – a, resultará em uma divisão exata, ou seja, terá resto igual a zero se, e somente se, a constante a for raiz do polinômio P(x).
Exemplo: Sem efetuar as divisões, prove que o polinômio P(x) = x4 - 4x3 + 4x2 - 4x +3 é divisível por x - 3 e x - i.
As divisões dadas favorecem a aplicação do Teorema de D’Alembert, dessa forma podemos afirmar que: a constante a será raiz do polinômio P(x) se, somente se, o resto da divisão for igual a zero. Dessa forma, basta aplicarmos o Teorema do Resto.
Para divisor igual a x – 3, a = 3.
P(3) = 34 – 4 . 33 + 4 . 32 – 4 . 3 + 3
P(3) = 81 – 4 . 27 + 4 . 9 – 12 + 3
P(3) = 81 – 108 + 36 – 12 + 3
P(3) = -27 + 36 – 12 + 3
P(3) = 9 – 12 + 3
P(3) = -3 + 3
P(3) = 0
Portanto, o polinômio P(x) = x4 - 4x3 + 4x2 - 4x +3 é divisível por x – 3.
Para divisor igual a x – i, a = i.
P(i) = i4 – 4 . i3 + 4 . i2 – 4 . i + 3
P(i) = 1 – 4 . (-i) + 4 . (-1) – 4i + 3
P(i) = 1 + 4i – 4 – 4i + 3
P(i) = 1 – 4 + 3
P(i) = - 3 + 3
P(i) = 0
Portanto, o polinômio P(x) = x4 - 4x3 + 4x2 - 4x +3 é divisível por x – i.
www.mundoeducacao.com.br
Conjuntos Numéricos
Os números são indispensáveis no estudo da Matemática e, por isso, são organizados em conjuntos que possuem características próprias. Ao longo da evolução da Matemática, os números foram surgindo e sendo classificados como Naturais, Inteiros, Racionais, Irracionais e Reais. Vamos conhecer cada conjunto e suas propriedades a fim de obtermos sucesso em estudos futuros.
Conjunto dos Números Naturais
Os números Naturais são representados pela letra maiúscula N e engloba todos os números inteiros positivos e o zero. Observe:
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25,...}
O conjunto dos números Naturais é considerado infinito, isto é, não possui fim. Uma característica dos números Naturais é a utilização na contagem de objetos.
Conjunto dos Números Inteiros
Os números Inteiros são representados pela letra maiúscula Z e aborda todos os números inteiros positivos, negativos e o zero. Veja:
Z = {..., -10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,...}
O conjunto dos números Inteiros é considerado infinito. Como característica dos algarismos Inteiros, temos as representações de números negativos, como medidas de temperatura, saldos negativos, situações abaixo do nível do mar entre outras.
Conjunto dos Números Racionais
Os números racionais são representados pela letra maiúscula Q e agrupa todos os números inteiros positivos, negativos, o zero, números na forma decimal e os números fracionários, aqueles na forma de a/b com b ≠ 0.
Todos os números em que a divisão é uma dízima periódica são considerados números racionais. Exemplos:
As dízimas periódicas são números resultados de uma divisão, onde à direita da vírgula temos a formação de períodos. Observe:
A dízima 0,666... possui como período o número 6.
A dízima 0,727272... possui como período o número 72.
Toda dízima periódica possui uma representação na forma de fração. Veja:
Os números Racionais são utilizados para representar partes de um inteiro. Esse conjunto também é considerado infinito.
Conjunto dos Números Irracionais
Os números Irracionais são representados pela letra maiúscula I, o grupo é formado pelos números que não possuem representação fracionária. Os números são considerados dízimas não periódicas, isto é, são infinitos, mas a sua composição não fornece períodos.
√2 = 1,4142135623730950488016887242097...
√3 = 1,7320508075688772935274463415059...
–√7 = 2,6457513110645905905016157536393...
–√11 = 3,3166247903553998491149327366707...
Conjunto dos Números Reais
O conjunto dos números Reais é formado pela união dos conjuntos dos números Naturais, Inteiros, Racionais e Irracionais.
Conjunto dos Números Primos
Esse conjunto reúne todos os números Naturais que são divisíveis somente por 1 e por ele mesmo. Observe o Crivo de Eratóstenes a seguir, ele apresentará em azul os números primos de 1 a 100.
O número 2 é o único número primo par. Possui como divisores os números 1 e 2. Observe que todos os números primos indicados obedecem a essa característica.
www.bancodeconcursos.com
Conjunto dos Números Naturais
Os números Naturais são representados pela letra maiúscula N e engloba todos os números inteiros positivos e o zero. Observe:
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25,...}
O conjunto dos números Naturais é considerado infinito, isto é, não possui fim. Uma característica dos números Naturais é a utilização na contagem de objetos.
Conjunto dos Números Inteiros
Os números Inteiros são representados pela letra maiúscula Z e aborda todos os números inteiros positivos, negativos e o zero. Veja:
Z = {..., -10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,...}
O conjunto dos números Inteiros é considerado infinito. Como característica dos algarismos Inteiros, temos as representações de números negativos, como medidas de temperatura, saldos negativos, situações abaixo do nível do mar entre outras.
Conjunto dos Números Racionais
Os números racionais são representados pela letra maiúscula Q e agrupa todos os números inteiros positivos, negativos, o zero, números na forma decimal e os números fracionários, aqueles na forma de a/b com b ≠ 0.
Todos os números em que a divisão é uma dízima periódica são considerados números racionais. Exemplos:
As dízimas periódicas são números resultados de uma divisão, onde à direita da vírgula temos a formação de períodos. Observe:
A dízima 0,666... possui como período o número 6.
A dízima 0,727272... possui como período o número 72.
Toda dízima periódica possui uma representação na forma de fração. Veja:
Os números Racionais são utilizados para representar partes de um inteiro. Esse conjunto também é considerado infinito.
Conjunto dos Números Irracionais
Os números Irracionais são representados pela letra maiúscula I, o grupo é formado pelos números que não possuem representação fracionária. Os números são considerados dízimas não periódicas, isto é, são infinitos, mas a sua composição não fornece períodos.
√2 = 1,4142135623730950488016887242097...
√3 = 1,7320508075688772935274463415059...
–√7 = 2,6457513110645905905016157536393...
–√11 = 3,3166247903553998491149327366707...
Conjunto dos Números Reais
O conjunto dos números Reais é formado pela união dos conjuntos dos números Naturais, Inteiros, Racionais e Irracionais.
Conjunto dos Números Primos
Esse conjunto reúne todos os números Naturais que são divisíveis somente por 1 e por ele mesmo. Observe o Crivo de Eratóstenes a seguir, ele apresentará em azul os números primos de 1 a 100.
O número 2 é o único número primo par. Possui como divisores os números 1 e 2. Observe que todos os números primos indicados obedecem a essa característica.
www.bancodeconcursos.com
Assinar:
Comentários (Atom)