Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Alguns exemplos cotidianos de reação química
Existem muitos exemplos de reações químicas no cotidiano. Entre eles estão a formação da ferrugem num pedaço de palha de aço, o apodrecimento dos alimentos, a produção de húmus no solo, a queima de gás num fogão e de gasolina, álcool ou óleo diesel no motor de um veículo.
A ocorrência de uma reação química nem sempre é fácil de perceber. Algumas só podem ser percebidas em laboratórios suficientemente equipados para separar componentes das misturas obtidas e determinar as suas propriedades. Há, contudo, algumas evidências que, estão, de modo geral, associadas à ocorrência de reações químicas e que são, portanto, pistas que podem indicar sua ocorrência. Entre essas evidências estão:
- liberação de calor – por exemplo, nas combustões;
- mudança de cor – por exemplo, quando um alvejante é derrubado, por descuido, num roupa colorida;
- mudança de odor – por exemplo, quando frutas, carnes e outros alimentos se estragam;
- liberação de gás – por exemplo, ao jogar um comprimido efervescente em água.
Reagente e produtos
As substâncias inicialmente presentes num sistema e que se transformam em outras devido à ocorrência de uma reação química são denominadas reagentes. E as novas substâncias produzidas são chamadas de produtos.
Assim, por exemplo:
Em equação:

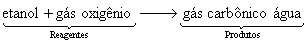
Em palavras: Os reagentes etanol e gás oxigênio reagem para formar os produtos gás carbônico e água.
Em equação:

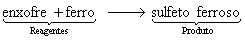
Em palavras: Os reagentes enxofre e ferro reagem para formar o produto sulfeto ferroso.
Lei da conservação da Massa, de Lavoisier
Esta lei foi elaborada, em 1774, pelo químico francês Antoine Laurent Lavoisier. Os estudos experimentais realizados por Lavoisier levaram-no a concluir que numa reação química, que se processa num sistema fechado, a soma das massas dos reagentes é igual à soma das massas dos produtos:
m (reagentes) = m (produtos)
Assim, por exemplo, quando 2 gramas de hidrogênio reagem com 16 gramas de oxigênio verifica-se a formação de 18 gramas de água; quando 12 gramas de carbono reagem com 32 gramas de oxigênio ocorre a formação de 44 gramas de gás carbônico.
Essa lei, inclusive, incorporou-se aos "saberes populares", sendo frequentemente enunciada como:
"Na natureza nada se cria, nada se perde, tudo se transforma."
Lei das proporções constantes (lei de Proust)
Esta lei foi elaborada, em 1797, pelo químico Joseph Louis Proust. Ele verificou que as massas dos reagentes e as massas dos produtos que participam de uma reação química obedecem sempre a uma proporção constante. Esta proporção é característica de cada reação e independente da quantidade das substâncias que são colocadas para reagir. Assim, para a reação entre hidrogênio e oxigênio formando água, os seguintes valores experimentais podem ser obtidos:
Experimento
|
hidrogênio (g)
|
oxigênio (g)
|
água (g)
|
I
|
10
|
80
|
90
|
II
|
2
|
16
|
18
|
III
|
1
|
8
|
9
|
IV
|
0,4
|
3,2
|
3,6
|
Observe que:
- para cada reação, a massa do produto é igual à massa dos reagentes, o que concorda com a lei de Lavoisier;
- as massas dos reagentes e do produto que participam das reações são diferentes, mas as relações massa de oxigênio/massa de hidrogênio, massa de água/massa de hidrogênio e massa de água/massa de oxigênio são sempre constantes.
Experimento
|
m oxigênio/m hidrogênio
|
m água/m hidrogênio
|
m água/oxigênio
|
I
|
8/10 = 8
|
90/10 = 9
|
90/80 = 1,125
|
II
|
16/2 = 8
|
18/2 = 8
|
18/16 = 1,125
|
III
|
8/1 = 8
|
9/1 = 9
|
9/8 = 1,125
|
IV
|
3,2/0,4 = 8
|
3,6/0,4 = 9
|
3,6/3,2 = 1,125
|
No caso das reações de síntese, isto é, aquelas que originam uma substância, a partir de seus elementos constituintes, o enunciado da lei de Proust pode ser o seguinte:
Resumindo:
A proporção, em massa, dos elementos que participam da composição de uma substância é sempre constante e independe do processo químico pelo qual a substância é obtida.
Equações químicas
Os químicos utilizam expressões, chamadas equações químicas, para representar as reações químicas.
Para se escrever uma equação química é necessário:
- saber quais substâncias são consumidas (reagentes) e quais são formadas (produtos);
- conhecer as fórmulas dos reagentes e dos produtos;
- escrever a equação sempre da seguinte forma: reagentes => produtos
- quando mais de um reagente, ou mais de um produto, participarem da reação, as fórmulas das substâncias serão separadas pelo sinal "+ ";
- se for preciso, colocar números, chamados coeficientes estequiométricos, antes das fórmulas das substâncias de forma que a equação indique a conservação dos átomos. Esse procedimento é chamado balanceamento ou acerto de coeficientes de uma equação.
|
Utilizando as regras acima para representar a formação da água temos:
- reagentes: hidrogênio e oxigênio;
- produto: água.
- fórmulas das substâncias: hidrogênio: H2; oxigênio: 02; água: H20.
- equação: H2 + 02
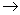 H2O.
H2O.
Acerto dos coeficientes: a expressão acima indica que uma molécula de hidrogênio (formada por dois átomos) reage com uma molécula de oxigênio (formada por dois átomos) para formar uma molécula de água (formada por dois átomos de hidrogênio e um de oxigênio). Vemos, portanto, que a expressão contraria a lei da conservação dos átomos (lei da conservação das massas), pois antes da reação existiam dois átomos de oxigênio e, terminada a reação, existe apenas um. No entanto, se ocorresse o desaparecimento de algum tipo de átomo a massa dos reagentes deveria ser diferente da massa dos produtos, o que não é verificado experimentalmente.
Como dois átomos de oxigênio (na forma de molécula 02) interagem, é lógico supor que duas moléculas de água sejam formadas. Mas como duas moléculas de água são formadas por quatro átomos de hidrogênio, serão necessárias duas moléculas de hidrogênio para fornecer essa quantidade de átomos. Assim sendo, o menor número de moléculas de cada substância que deve participar da reação é: hidrogênio, duas moléculas; oxigênio, uma molécula; água, duas moléculas.
A equação química que representa a reação é: 2H2 + 102 => 2 H20
Que é lida da seguinte maneira: duas moléculas de hidrogênio reagem com uma molécula de oxigênio para formar duas moléculas de água.
Classificação das reações químicas
As reações químicas podem ser classificadas de várias maneiras. A mais comum é aquela que utiliza como parâmetro os tipos de substâncias reagentes e resultantes.
Síntese ou adição
Nesta reação, dois ou mais reagentes (A e B) se combinam, formando apenas um produto (AB).
Alguns exemplos:
Análise ou decomposição
É a reação em que apenas um reagente (AB) produz dois ou mais produtos (A e B).
Alguns exemplos:
Simples troca ou deslocamento
É a reação em que uma substância simples se combina com uma substância composta, formando outra substância simples e outra composta.
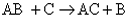 ou
ou 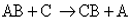
Alguns exemplos:
Dupla troca ou permutação
Neste tipo de reação ocorre uma troca entre duas substâncias compostas que se combinam, formando duas outras substâncias compostas.
Alguns exemplos:
Condição para que uma reação química ocorra
Para que duas ou mais substâncias reajam quimicamente, são necessárias as seguintes condições:
- suas moléculas devem estar dispostas de modo a conseguir o maior contato possível. Geralmente substâncias no estado gasoso reagem mais fácil e rapidamente do que substâncias no estado sólido;
- os reagentes devem ter afinidade química, isto é, uma certa “tendência a reagir” reciprocamente.
A energia das reações químicas
Nenhum átomo “surge do nada” ou “desaparece” durante uma reação química.
Se reações químicas são apenas um rearranjo de átomos, então, de onde vem a energia envolvida, por exemplo, numa queima?
Quando uma folha de papel queima, podemos observar que sua matéria se transforma, pois ocorre uma reação química. Percebemos, também, que nessa reação há liberação de luz e calor, que são formas de energia.
- De onde veio essa energia que foi liberada?
- Por que ela foi liberada?
- Pode haver uma reação que, ao invés de liberar, absorva calor?
A energia química
As substância possuem certa quantidade de energia armazenada, denominada energia química. Essa energia é proveniente de suas ligações químicas e das forças de atração e de repulsão entre os átomos que a compõem.
Como cada substância possui armazenada uma quantidade de energia química específica, há uma diferença entre os conteúdos energéticos de seus reagentes e de seus produtos.
Em função da energia química de reagentes e produtos, a reação pode ocorrer segundo duas formas distintas:
A energia dos reagentes é menor que a dos produtos.
Neste caso os reagentes terão que ganhar energia para se transformar em produtos.
|
A energia dos reagentes é maior que a dos produtos.
Neste caso os reagentes terão de liberar energia para se transformar em produtos.
|
A absorção e a liberação de energia normalmente ocorrem acompanhadas de absorção ou liberação de calor.
Os reagentes ganham energia para se transformar em produtos com maior energia ou podem perder energia para se transformar em produtos com menor energia.
Reações químicas que absorvem energia são chamadas endotérmicas e as que liberam energia são chamadas exotérmicas.
Quando os produtos possuem mais energia que os reagentes, sabemos que essas reações absorveram energia, isto é, elas normalmente ganham calor para ocorrerem. Um exemplo é a queima do açúcar para fazer a calda do pudim. Ao receber calor o açúcar se transforma em calda, e sua aparência e seu sabor mudam. Para que essa reação ocorra é necessário ceder energia ao sistema.
Já nas reações exotérmicas, a energia dos reagentes é maior que a dos produtos. Normalmente, os reagentes perdem calor para que a reação ocorra, o que acontece, por exemplo, na queima do papel. É fácil verificar que o sistema está liberando energia na forma de calor e luz.
É importante ressaltar que nem sempre a energia liberada e absorvida ocorre na forma de calor, um exemplo é a fotossíntese, em que a absorção de energia ocorre pela presença de luz (energia luminosa).
A velocidade das reações químicas
Como você já deve ter observado, algumas reações ocorrem mais rapidamente e outras mais lentamente. Portanto, as reações podem ser rápidas ou lentas e sua velocidade pode ser medida pela formação de produtos ou consumo de reagentes por unidade de tempo.
Suponha que na reação do
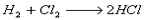
sejam formados 365 g de HCl, em 10 minutos.
A velocidade dessa reação pode ser calculada dividindo-se a massa da substância pelo tempo:
Essa velocidade pode ser calculada, ainda, em função dos reagentes; por exemplo, se foram consumidos 20 g de H2 nos mesmos 10 minutos, temos:
As unidades utilizadas nos exemplos podem ser outras. Gramas e minuto podem ser substituídos por litro e segundo. O importante é que sejam definidas e representadas de forma compreensível.
Fatores que interferem na velocidade da reação química
A velocidade de uma reação química depende de vários fatores: da superfície de contato entre os reagentes, da temperatura, da concentração das substâncias reagentes e da presença do catalisador.
É importante conhecer os fatores que influenciam na velocidade das reações químicas, para que possam ser controladas. Um exemplo bastante elucidativo é a forma como são conservados os alimentos, pois sua deterioração ocorre através de reações químicas.
Superfície de contato
Quanto maior a superfície de contato entre os reagentes, maior a velocidade de reação. Exemplo: os antiácidos efervescentes quando triturados se dissolvem mais rápido em água do que em forma de comprimido inteiro, isto porque a superfície de contato fica maior para reagir com a água
|
|  |
Concentração de reagentes
Quanto maior a concentração dos reagentes, mais rápida será a reação química. Essa propriedade está relacionada com o número de colisões entre as partículas. Exemplo: uma amostra de palha de aço reage mais rápido com ácido clorídrico concentrado do que com ácido clorídrico diluído.
Temperatura
De um modo geral, quanto maior a temperatura, mais rapidamente se processa a reação. Podemos acelerar uma reação lenta, submetendo os reagentes a uma temperatura mais elevada. Exemplo: se cozinharmos um alimento em panela de pressão ele cozinhará bem mais rápido, devido à elevação de temperatura em relação às panelas comuns.
Adição de catalisador
Catalisadores são substâncias com capacidade de acelerar determinadas reações químicas. Os catalisadores interagem com os reagentes, fazendo com que a reação entre estes seja mais fácil de ocorrer, ocasionando um aumento na formação de produtos por unidade de tempo.
Devido a essas características, os catalisadores são muito utilizados em indústrias químicas, pois quanto maior a velocidade de reação, mais eficiente é o processo e menor o tempo gasto para a obtenção de determinada substância.
Se deixarmos o peróxido de hidrogênio (H2O2) em um recipiente aberto, aos poucos vai ocorrer uma reação de decomposição em água e oxigênio:
Porém, se introduzirmos no recipiente uma placa de platina, a reação ocorre muito mais rapidamente.
www.sobiologia.com.br

