Números reais
O conjunto R
O conjunto de números reais é simbolizado pela letra R. Todo número inteiro ou decimal é considerado real.
Estrutura de R
Propriedades da adição
Associativa: (x + y) + z = x + (y + z)
Comutativa: x + y = y + x
Elemento neutro: x + 0 = 0 + x = x
Simétrico Aditivo ou aposto: x + (-x) = (-x) + x = 0
Propriedades de multiplicação
Associativa: (x. y) . z = x . (y. z) Comutativa: x . y = y. x
Elemento neutro: x . 1 = 1 . x = x
Simétrico multiplicativo ou inverso: x . x-1 = x-1 . x = 1
Propriedade distributiva da multiplicação em relação á adição
x . (y + z) = xy + xz
Propriedades da Relação de ordem
Reflexiva: x ≤ x
Anti-simétrica: x ≤ y e y ≤ x ⇒ x = y Transitiva: x ≤ y e y ≤ z ⇒ x ≤ z
Tricotomia ou ordem total: x < y ou x = y ou x > y
Compatibilidade com a adição: x ≤ y ⇒ x + z ≤ y + z
Compatibilidade com a multiplicação:
z > 0 logo, x ≤ y ⇒ x . z ≤ y . z
z < 0 logo, x ≤ z ⇒ x . z ≥ y . z
Valor absoluto
Considere . Sendo assim, o módulo de x (valor absoluto de x), é um número real positivo, representado por |x|. Este número é determinado desta maneira:
x ≥ 0 ⇒ |x| = x
x ≥ 0 ⇒ |x| = - x
sábado, 30 de novembro de 2019
Funções
Funções |
Dados dois conjuntos A e B não vazios , chama-se função (ou aplicação) de A em B, representada por
f : A ® B ; y = f(x) , a qualquer relação binária que associa a cada elemento de A ,
um único elemento de B .
um único elemento de B .
Portanto, para que uma relação de A em B seja uma função , exige-se que a cada x Î A esteja associado um único y Î B , podendo entretanto existir y Î B que não esteja associado a nenhum elemento pertencente ao conjunto A.
Obs : na notação y = f(x) , entendemos que y é imagem de x pela função f, ou seja:
y está associado a x através da função f.
y está associado a x através da função f.
Exemplos:
f(x) = 4x+3 ; então f(2) = 4.2 + 3 = 11 e portanto , 11 é imagem de 2 pela função f ;
f(5) = 4.5 + 3 = 23 , portanto 23 é imagem de 5 pela função f , f(0) = 4.0 + 3 = 3, etc.
f(x) = 4x+3 ; então f(2) = 4.2 + 3 = 11 e portanto , 11 é imagem de 2 pela função f ;
f(5) = 4.5 + 3 = 23 , portanto 23 é imagem de 5 pela função f , f(0) = 4.0 + 3 = 3, etc.
Para definir uma função , necessitamos de dois conjuntos (Domínio e Contradomínio ) e de uma fórmula ou uma lei que relacione cada elemento do domínio a um e somente um elemento do contradomínio .
Quando D(f) (domínio) Ì R e CD(f)(contradomínio) Ì R , sendo R o conjunto dos números reais , dizemos que a função f é uma função real de variável real . Na prática , costumamos considerar uma função real de variável real como sendo apenas a lei y = f(x) que a define , sendo o conjunto dos valores possíveis para x , chamado de domínio e o conjunto dos valores possíveis para y , chamado de conjunto imagem da função . Assim, por exemplo, para a função definida por y = 1/x , temos que o seu domínio é D(f) = R* , ou seja o conjunto dos reais diferentes de zero (lembre-se que não existe divisão por zero) , e o seu conjunto imagem é também R* , já que se y = 1/x , então x = 1/y e portanto y também não pode ser zero.
Nota: o símbolo Ì significa “contido em”.
Nota: o símbolo Ì significa “contido em”.
Dada uma função f : A ® B definida por y = f(x),
podemos representar os pares ordenados (x,y) Î f onde x Î A e y Î B ,num sistema de coordenadas cartesianas .
O gráfico obtido será o gráfico da função f .
Assim , por exemplo , sendo dado o gráfico cartesiano de uma função f , podemos dizer que:
podemos representar os pares ordenados (x,y) Î f onde x Î A e y Î B ,num sistema de coordenadas cartesianas .
O gráfico obtido será o gráfico da função f .
Assim , por exemplo , sendo dado o gráfico cartesiano de uma função f , podemos dizer que:
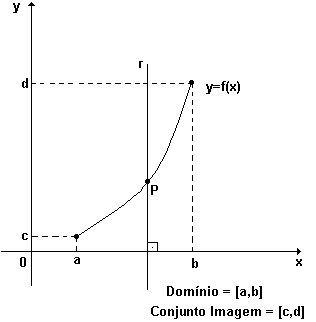
a ) a projeção da curva sobre o eixo dos x , nos dá o domínio da função .
b ) a projeção da curva sobre o eixo dos y , nos dá o conjunto imagem da função .
c ) toda reta vertical que passa por um ponto do domínio da função , intercepta o gráfico da função em no máximo um ponto .
b ) a projeção da curva sobre o eixo dos y , nos dá o conjunto imagem da função .
c ) toda reta vertical que passa por um ponto do domínio da função , intercepta o gráfico da função em no máximo um ponto .
Veja a figura abaixo, relativa aos ítens 1, 2 e 3 acima:
2 -Tipos de funções
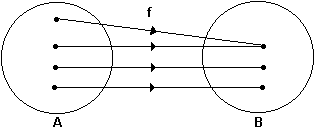
2.1 - Função sobrejetora
É aquela cujo conjunto imagem é igual ao contradomínio .
Exemplo:
Exemplo:
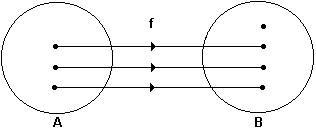
2.2 - Função injetora
Uma função y = f(x) é injetora quando elementos distintos do seu domínio , possuem imagens distintas,
isto é:
x1 ¹ x2 Þ f(x1) ¹ f(x2) .
isto é:
x1 ¹ x2 Þ f(x1) ¹ f(x2) .
Exemplo:
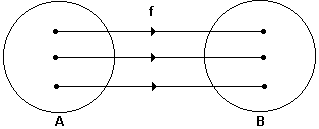
2.3 - Função bijetora
Uma função é dita bijetora , quando é ao mesmo tempo , injetora e sobrejetora .
Exemplo:
Exercícios resolvidos:
1 - Considere três funções f, g e h, tais que:
A função f atribui a cada pessoa do mundo, a sua idade.
A função g atribui a cada país, a sua capital
A função h atribui a cada número natural, o seu dobro.
A função f atribui a cada pessoa do mundo, a sua idade.
A função g atribui a cada país, a sua capital
A função h atribui a cada número natural, o seu dobro.
Podemos afirmar que, das funções dadas, são injetoras:
a) f, g e h
b) f e h
c) g e h
d) apenas h
e) nenhuma delas
a) f, g e h
b) f e h
c) g e h
d) apenas h
e) nenhuma delas
Solução:
Sabemos que numa função injetora, elementos distintos do domínio, possuem imagens distintas, ou seja:
x1 ¹ x2 Þ f(x1) ¹ f(x2) .
Sabemos que numa função injetora, elementos distintos do domínio, possuem imagens distintas, ou seja:
x1 ¹ x2 Þ f(x1) ¹ f(x2) .
Logo, podemos concluir que:
f não é injetora, pois duas pessoas distintas podem ter a mesma idade.
g é injetora, pois não existem dois países distintos com a mesma capital.
h é injetora, pois dois números naturais distintos, possuem os seus dobros também distintos.
Assim é que concluímos que a alternativa correta é a de letra C.
f não é injetora, pois duas pessoas distintas podem ter a mesma idade.
g é injetora, pois não existem dois países distintos com a mesma capital.
h é injetora, pois dois números naturais distintos, possuem os seus dobros também distintos.
Assim é que concluímos que a alternativa correta é a de letra C.
2 - Seja f uma função definida em R - conjunto dos números reais - tal que
f(x - 5) = 4x. Nestas condições, pede-se determinar f(x + 5).
f(x - 5) = 4x. Nestas condições, pede-se determinar f(x + 5).
Solução:
Vamos fazer uma mudança de variável em f(x - 5) = 4x, da seguinte forma:
x - 5 = u \ x = u + 5
Substituindo agora (x - 5) pela nova variável u e x por (u + 5), vem:
f(u) = 4(u + 5) \ f(u) = 4u + 20
Vamos fazer uma mudança de variável em f(x - 5) = 4x, da seguinte forma:
x - 5 = u \ x = u + 5
Substituindo agora (x - 5) pela nova variável u e x por (u + 5), vem:
f(u) = 4(u + 5) \ f(u) = 4u + 20
Ora, se f(u) = 4u + 20, teremos:
f(x + 5) = 4(x+5) + 20 \ f(x+5) = 4x + 40
3 – UEFS 2005-1 ) Sabendo-se que a função real f(x) = ax + b é tal que f(2x2 + 1) = - 2x2 + 2,
para todo x Î R, pode-se afirmar que b/a é igual a
a) 2
b) 3/2
c) 1/2
d) -1/3
e) -3Solução:
Ora, se f(x) = ax + b, então f(2x2 + 1) = a(2x2 + 1) + b
Como f(2x2 + 1) = - 2x2 + 2, vem, igualando:
a(2x2 + 1) + b = - 2x2 + 2
Efetuando o produto indicado no primeiro membro, fica:2ax2 + a + b = -2x2 + 2
Então, poderemos escrever: 2a = -2 \ a = -2 /2 = -1
E, também, a + b = 2 ; como a = -1, vem substituindo: (-1) + b = 2 \ b = 2 + 1 = 3
Logo, o valor procurado a/b será a/b = -1 / 3 , o que nos leva tranquilamente à alternativa D.
f(x + 5) = 4(x+5) + 20 \ f(x+5) = 4x + 40
3 – UEFS 2005-1 ) Sabendo-se que a função real f(x) = ax + b é tal que f(2x2 + 1) = - 2x2 + 2,
para todo x Î R, pode-se afirmar que b/a é igual a
a) 2
b) 3/2
c) 1/2
d) -1/3
e) -3Solução:
Ora, se f(x) = ax + b, então f(2x2 + 1) = a(2x2 + 1) + b
Como f(2x2 + 1) = - 2x2 + 2, vem, igualando:
a(2x2 + 1) + b = - 2x2 + 2
Efetuando o produto indicado no primeiro membro, fica:2ax2 + a + b = -2x2 + 2
Então, poderemos escrever: 2a = -2 \ a = -2 /2 = -1
E, também, a + b = 2 ; como a = -1, vem substituindo: (-1) + b = 2 \ b = 2 + 1 = 3
Logo, o valor procurado a/b será a/b = -1 / 3 , o que nos leva tranquilamente à alternativa D.
Agora resolva este:A função f em R é tal que f(2x) = 3x + 1. Determine 2.f(3x + 1).
Resp: 9x + 5
Resp: 9x + 5
3 - Paridade das funções
3.1 - Função par
A função y = f(x) é par, quando " x Î D(f) , f(- x ) = f(x) , ou seja, para todo elemento do seu domínio,
f( x ) = f ( - x ). Portanto , numa função par, elementos simétricos possuem a mesma imagem. Uma conseqüência desse fato é que os gráficos cartesiano das funções pares, são curvas simétricas em relação ao eixo dos y ou eixo das ordenadas.
O símbolo " , lê-se “qualquer que seja”.
f( x ) = f ( - x ). Portanto , numa função par, elementos simétricos possuem a mesma imagem. Uma conseqüência desse fato é que os gráficos cartesiano das funções pares, são curvas simétricas em relação ao eixo dos y ou eixo das ordenadas.
O símbolo " , lê-se “qualquer que seja”.
Exemplo:
y = x4 + 1 é uma função par, pois f(x) = f(-x), para todo x.
Por exemplo, f(2) = 24 + 1 = 17 e f(- 2) = (-2)4 + 1 = 17
y = x4 + 1 é uma função par, pois f(x) = f(-x), para todo x.
Por exemplo, f(2) = 24 + 1 = 17 e f(- 2) = (-2)4 + 1 = 17
O gráfico abaixo, é de uma função par.
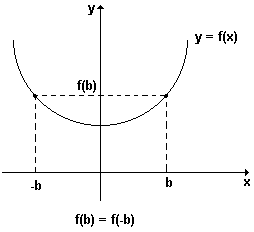
4.2 - Função ímpar
A função y = f(x) é ímpar , quando " x Î D(f) , f( - x ) = - f (x) , ou seja, para todo elemento do seu domínio, f( - x) = - f( x ). Portanto, numa função ímpar, elementos simétricos possuem imagens simétricas. Uma conseqüência desse fato é que os gráficos cartesianos das funções ímpares, são curvas simétricas em relação ao ponto (0,0), origem do sistema de eixos cartesianos.
Exemplo:
y = x3 é uma função ímpar pois para todo x, teremos f(- x) = - f(x).
Por exemplo, f( - 2) = (- 2)3 = - 8 e - f( x) = - ( 23 ) = - 8.
y = x3 é uma função ímpar pois para todo x, teremos f(- x) = - f(x).
Por exemplo, f( - 2) = (- 2)3 = - 8 e - f( x) = - ( 23 ) = - 8.
O gráfico abaixo é de uma função ímpar:
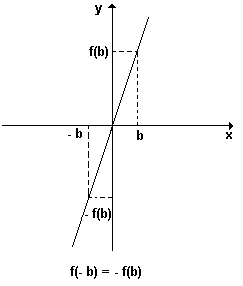
Nota: se uma função y = f(x) não é par nem ímpar, diz-se que ela não possui paridade.
Exemplo:
O gráfico abaixo, representa uma função que não possui paridade, pois a curva não é simétrica em relação ao eixo dos x e, não é simétrica em relação à origem.
Exemplo:
O gráfico abaixo, representa uma função que não possui paridade, pois a curva não é simétrica em relação ao eixo dos x e, não é simétrica em relação à origem.
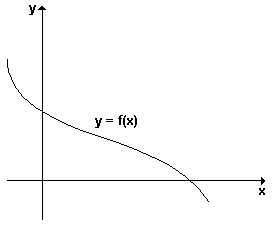
O governo de Itamar Franco
Professor de Matemática no Colégio Estadual Dinah Gonçalves
E Biologia na rede privada de Salvador-Bahia www.youtube.com/accbarroso1
Professor Antonio Carlos carneiro Barroso
email accbarroso@hotmail.com
Extraído de http://www.alunosonline.com.br
O governo de Itamar Franco
Itamar Franco, "pai" do Plano Real, que estabilizou a economia brasileira.
A principal medida adotada no governo Itamar foi a criação de um plano para barrar o crescimento da inflação: o Plano Real. Idealizado e organizado pelo Ministro da Fazenda (e posteriormente, Presidente da República) Fernando Henrique Cardoso, o Plano Real obteve êxito, reduzindo a inflação de 50% para 4%, em um mês. No dia 21 de abril de 1993, o Presidente Itamar Franco convocou um plebiscito para escolher a nova forma de governo: se manteria o presidencialismo e a república, ou se retornaria à monarquia e ao parlamentarismo. O regime republicano e presidencialista foi escolhido por uma maioria esmagadora dos votos.
Um fato curioso, acontecido no governo Itamar, foi sua sugestão à fábrica alemã Volkswagen, a retomar a fabricação do Fusca, carro muito popular nas décadas de 60 e 70, no Brasil. Itamar visava aquecer a venda de automóveis, tornando-os mais acessíveis aos brasileiros. A fábrica havia parado de fabricar o Fusca em 1978 e, a pedido do presidente, retomou sua fabricação (que cessou em 1996). O carro, apelidado de Fusca do Itamar, não atendeu às necessidades do povo, mas a ideia de popularização dos veículos foi adotada por outras fábricas.
O governo de Itamar foi curto (cerca de dois anos), mas foi o suficiente para levantar a economia nacional e, consequentemente, o orgulho dos brasileiros, ferido nos anos de chumbo da ditadura e destroçado no governo corrupto de Collor. Itamar alcançou índices tão altos de popularidade e aprovação, que seu apoio foi imprescindível para a eleição de seu Ministro e sucessor, Fernando Henrique Cardoso, nas eleições presidenciais de 1994.
Assinar:
Postagens (Atom)