Áreas das Figuras Planas Triângulos,Losangos e Trapézios aula2

Determinante

a) Menor complementar

O menor complementar de um elemento é o determinante da sua matriz quadrada. Para obtermos o menor complementar basta eliminar a linha e a coluna que o elemento pertence.

Obs.: todos elementos de uma matriz possui um menor complementar.

Exemplo:
Considere a matriz abaixo:



Qual a utilidade?

Através do Teorema de Laplace é possível obter o determinante de uma matriz de ordem n utilizando o determinante de matrizes de ordem n - 1. Portanto é possível abaixar a ordem.

e) Que fila escolhe?

Conforme o teorema, o determinante pode ser obtido por meio de qualquer fila. Para facilitar, devemos escolher a fila que tiver maior quantidade de zeros.

Propriedades dos Determinantes

Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso

Colégio Estadual Dinah Gonçalves

email accbarroso@hotmail.com

 www.ensinodematemtica.blogspot.com.br

www.accbarrosogestar.blogspot.com.br 

As propriedades envolvendo determinantes facilitam o cálculo de seu valor em matrizes que se enquadram nessas condições. Observe as propriedades:

1ª propriedade

Ao observar uma matriz e verificar que os elementos de uma linha ou uma coluna são iguais a zero, o valor do seu determinante também será zero.

2ª propriedade
Caso ocorra igualdade de elementos entre duas linhas ou duas colunas, o determinante dessa matriz será nulo.

3ª propriedade
Verificadas em uma matriz duas linhas ou duas colunas com elementos de valores proporcionais, o determinante terá valor igual à zero. Observe a propriedade entre a 1ª e a 2ª linha.

4ª propriedade
Ao multiplicarmos todos os elementos de uma linha ou coluna de uma matriz por um número K, o seu determinante fica multiplicado por K.

Os elementos da 1ª linha de P foram multiplicados por 2, então: det P’ = 2 * det P

5ª propriedade
Caso uma matriz quadrada A seja multiplicada por um número real k, seu determinante passa a ser multiplicado por kⁿ.

det (k*A) = kⁿ * det A


6ª propriedade

O valor do determinante de uma matriz R é igual ao determinante da matriz da transposta de R, det R = det (R^t).

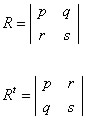
det R = ps -- qr

det Rt = ps – rq


7ª propriedade
Ao trocarmos duas linhas ou duas colunas de posição de uma matriz, o valor do seu determinante passa a ser oposto ao determinante da anterior.



8ª propriedade

O determinante de uma matriz triangular é igual à multiplicação dos elementos da diagonal principal.
Lembre-se que em uma matriz triangular, os elementos acima ou abaixo da diagonal principal são iguais a zero.

9ª propriedade
Considerando duas matrizes quadradas de ordem iguais e AB matriz produto, temos que: det (AB) = (det A) * (det B), conforme teorema de Binet.


10ª propriedade

Ao multiplicarmos todos os elementos de uma linha ou de uma coluna pelo mesmo número e adicionarmos os resultados aos elementos correspondentes de outra linha ou coluna, formamos a matriz B, onde ocorre a seguinte igualdade: det A = det B. Esse teorema é atribuído a Jacobi.

Por Marcos Noé
Graduado em Matemática

Matriz Identidade

Matriz Identidade

A matriz quadrada A = (aij)n x n definida por:



recebe o nome de matriz identidade de ordem n, simbolicamente representada por In.
Portanto:


extraido de www.colegioweb.com.br

Trigonometria, Fórmulas Derivadas da Fundamentais

Já sabemos as cinco fórmulas fundamentais da Trigonometria, a saber:
Dado um arco trigonométrico x , temos:
Fórmula I: Relação Fundamental da Trigonometria.
sen²x + cos²x = 1
[o mesmo que (senx)² + (cosx)² = 1]
Fórmula II: Tangente.

Fórmula III: Cotangente.

Fórmula IV: Secante.

Fórmula V: Cossecante.

Nota: considere nas fórmulas acima, a impossibilidade absoluta da divisão por ZERO.
Assim, por exemplo, se cosx = 0, não existe a secante de x ; se sen x = 0, não existe a cosec x, ...
Para deduzir duas outras fórmulas muito importantes da Trigonometria, vamos partir da Fórmula I acima, inicialmente dividindo ambos os membros por cos² x¹ 0.
Teremos:

Das fórmulas anteriores, concluiremos inevitavelmente a seguinte fórmula que relaciona a tangente e a secante de um arco trigonométrico x:
tg²x + 1 = sec²x
Se ao invés de dividirmos por cos²x, dividíssemos ambos os membros por sen²x, chegaríamos a:
cotg²x + 1 = cosec²x
As duas fórmulas anteriores, são muito importantes para a solução de exercícios que comparecem nos vestibulares, e merece por isto, uma memorização. Aliás, as sete fórmulas anteriores, têm necessariamente de ser memorizadas, e isto é apenas o início! A Trigonometria, infelizmente, depende de memorizações de fórmulas, mas, se você souber deduzi-las, como estamos tentando mostrar aqui, as coisas ficarão muito mais fáceis! Portanto, fique tranqüilo(a).

Matrizes

Hipérbole

Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso

Colégio Estadual Dinah Gonçalves

email accbarroso@hotmail.com        

 www.ensinodematemtica.blogspot.com.br

www.accbarrosogestar.blogspot.com.br 

     

EQUAÇÃO DA HIPÉRBOLE COM CENTRO NA ORIGEM

Considere uma hipérbole na qual os focos pertencem ou ao eixo das abscissas ou ao eixo das ordenadas, e o centro é a origem O (0, 0). Considere também um ponto P (x, y) qualquer da curva. Com esses dados, obteremos, depois de alguns procedimentos matemáticos, a equação reduzida da hipérbole.



Aplicações

01. Obter a equação da elipse de focos F1(-2,0) e F2(2,0), sabendo ainda que seu semi-eixo menor é b = 3.

Solução:

De início, note que os focos pertencem ao eixo Ox (isto é, o eixo maior é horizontal) e que a semidistância focal é igual a 2. Então:





02. Determinar a equação da hipérbole de focos F1(-3,0) e F2(3,0) cujo semi-eixo real é a = 2.

Solução

Das: coordenadas dos focos concluiu-se que a hipérbole tem seu eixo real situado no eixo Ox e que a semi distância focal é c = 3. Assim,

extraido de www.colegioweb.com.br

Matrizes

Matriz adição

Matriz subtração

Matriz

Propriedades dos determinantes

Marcelo Rigonatto

Determinantes

O cálculo dos determinantes pode ser facilitado se analisarmos as características e propriedades de algumas matrizes. Há algumas propriedades que, se bem observadas, podem fazer com que economizemos tempo na realização desses cálculos. Vejamos quais são essas propriedades e como elas podem nos ajudar.

Propriedade 1.

Quando todos os elementos de uma linha ou coluna são iguais a zero, o determinante da matriz é nulo.

Exemplo:

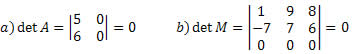
Propriedade 2.

Se duas linhas ou duas colunas de uma matriz forem iguais, seu determinante será nulo.

Exemplo:

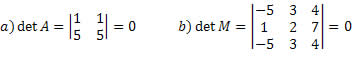
Propriedade 3.

Se duas linhas ou duas colunas de uma matriz forem proporcionais, então seu determinante será nulo.

Exemplo:

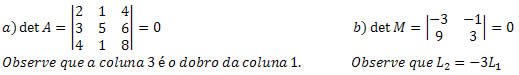
Propriedade 4.

Se todos os elementos de uma linha ou de uma coluna da matriz forem multiplicados por um número real p qualquer, então seu determinante também será multiplicado por p.

Exemplo:

Propriedade 5.

Se uma matriz A, quadrada de ordem m, for multiplicada por um número real p qualquer, então seu determinante será multiplicado por p^m.

det (p∙A) = p^m∙det A

Exemplo:

Propriedade 6.

O determinante de uma matriz é igual ao determinante de sua transposta.
det A=det A^t

Exemplo:

Propriedade 7.

Se trocarmos de posição duas linhas ou duas colunas de uma matriz, seu determinante será o oposto da matriz anterior.

Exemplo:

Propriedade 8.

Se os elementos acima ou abaixo da diagonal principal forem iguais a zero, então o determinante da matriz será o produto dos elementos da diagonal principal.

Exemplo:


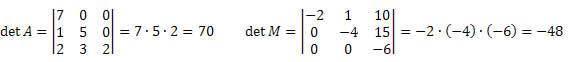
Propriedade 9.

O determinante do produto de duas matrizes é igual ao produto dos determinantes de cada uma delas.
det (A∙B) = det A ∙ det B

Propriedade 10.

Teorema de Jacob: o determinante de uma matriz não se altera quando somamos aos elementos de uma fila uma combinação linear dos elementos correspondentes de filas paralelas.

Exemplo:

Se somarmos os elementos da coluna 1 com o dobro dos elementos da coluna 2, o determinante não irá se alterar.

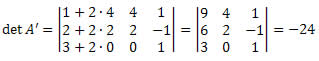
Regra de Sarrus

Regra de Sarrus

O cálculo do determinante de 3ª ordem pode ser feito por meio de um dispositivo prático, denominado regra de Sarrus.

Acompanhe como aplicamos essa regra para .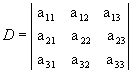

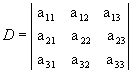1º passo: Repetimos as duas primeiras colunas ao lado da terceira:

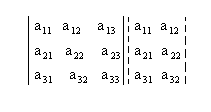
2º passo: Encontramos a soma do produto dos elementos da diagonal principal com os dois produtos obtidos pela multiplicação dos elementos das paralelas a essa diagonal (a soma deve ser precedida do sinal positivo):

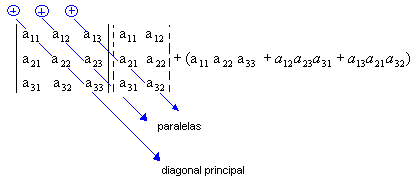
3º passo: Encontramos a soma do produto dos elementos da diagonal secundária com os dois produtos obtidos pela multiplicação dos elementos das paralelas a essa diagonal ( a soma deve ser precedida do sinal negativo):

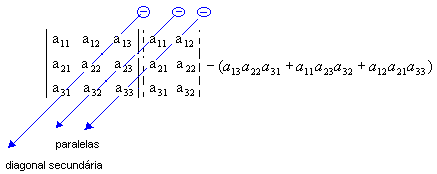
Assim:

Observação: Se desenvolvermos esse determinante de 3ª ordem aplicando o Teorema de Laplace, encontraremos o mesmo número real.

Determinante de ordem n > 3

Vimos que a regra de Sarrus é válida para o cálculo do determinante de uma matriz de ordem 3. Quando a matriz é de ordem superior a 3, devemos empregar o Teorema de Laplace para chegar a determinantes de ordem 3 e depois aplicar a regra de Sarrus.

Plano de curso de Matemática de acordo com o BNCC 2º ano Ensino Médio

Colégio Estadual Dinah Gonçalves

Planejamento anual 2020

Disciplina: Matemática

Aulas semanais: 3

Série: 2º ano Ensino Médio

Turnos: 

Professor Antonio Carlos Carneiro Barroso

01 – COMPETÊNCIAS GERAIS DA BASE NACIONAL COMUM CURRICULAR A SEREM TRABALHADAS NO DECORRER DO ANO

As competências gerais da BNCC, apresentadas a seguir, inter-relacionam-se e desdobram-se no tratamento didático proposto para as três etapas da Educação Básica (Educação Infantil, Ensino Fundamental e Ensino Médio), articulando-se na construção de conhecimentos, no desenvolvimento de habilidades e na formação de atitudes e valores, nos termos da LDB.

1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.

4. Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.

6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.

7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.

9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

02 – Temas a serem trabalhados:

Previsão	Eixo temático/ Tema do CBC	Tópicos
1º Bimestre	Unidade I: Matrizes Unidade I: Trigonometria	1) Estudo das Matrizes                                                   6) Função Seno 2) Determinantes                                                            7) Função Cosseno 3) Sistemas Lineares                                                       8) Função Tangente 4) Circunferência trigonométrica.                                9) Lei dos senos. 5) Razões trigonométricas na circunferência.          10) Lei dos cossenos.
2º Bimestre	Unidade II: Geometria Espacial	1) Área de figuras planas                                              3) pirâmides 2) prisma                                                                          4) cilindro
3º Bimestre	Unidade II: Geometria Espacial Unidade III: Analise combinatória	5) cone                                                                            6) esfera 1) princípio fundamental da contagem 2) fatorial 3) agrupamento simples
4º Bimestre	Unidade III: Analise combinatória; Unidade III: Probabilidade.	4)  Permutação                                                            6) Combinação 5) Arranjo 1) Definição Probabilidade                                       4) Probabilidade da interseção de dois eventos 2) Probabilidade da união de dois eventos           5) Eventos independentes. 3) probabilidade condicional

03 – Metodologia:

Aulas expositivas;

Trabalhos em equipes;

Vídeo aulas;

Class room (sala digital).

    04 – Recursos didáticos:

- Lousa, giz;

- Instrumentos de medidas;

- Jornais e revistas;

- Jogos.(xadrez) ;

-software;

-lousa digital.

    05 – Avaliação da aprendizagem:

-Participação dos alunos em sala de aula;

- Caderno (organização);

- Relatórios;

- Provas;

-Tarefas;

-disciplina

0bservações:

As turmas serão trabalhadas de formas diferenciadas conforme a necessidade verificada pelo professor em sua turma ou mesmo turno, no entanto, o planejamento anual será geral para a série ou ano em questão. Cabe assim ao professor, junto à supervisão, repensarem em ações para adaptações necessárias conforme surgirem as necessidades de intervenção;

Os projetos a serem desenvolvidos nas turmas surgirão com o decorrer do desenvolvimento dos conteúdos a serem trabalhados e em época oportuna. Serão apresentados aos demais professores da turma para um possível trabalho cooperativo visando a interdisciplinaridade ou ainda, a possibilidade da transdisciplinaridade.

As bissetrizes dos quadrantes

O plano cartesiano é formado por dois eixos perpendiculares que se cruzam na origem das coordenadas (0,0), estabelecendo quatro quadrantes. A intersecção perpendicular dos eixos forma ângulos de 90º.

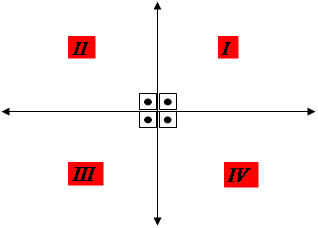
No plano cartesiano, ao traçarmos uma reta, que passa pelo ponto (0,0) formando um ângulo de 45º com a abscissa (eixo horizontal), estamos dividindo um quadrante ao meio e determinando a sua bissetriz.

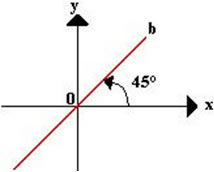
Podemos traçar as bissetrizes dos quadrantes de duas formas: bissetriz dos quadrantes pares e bissetriz dos quadrantes ímpares.


Bissetriz dos quadrantes ímpares

A bissetriz dos quadrantes ímpares é determinada por uma reta que intercepta o ponto (0,0) traçando as bissetrizes dos quadrantes I e III.

O coeficiente angular será igual a m = tg 45° = 1. Um dos seus pontos será (0,0) e todos os outros pontos pertencentes à reta b terão as ordenadas e abscissas iguais, por exemplo, (4,4), (5,5), (6,6), (7,7),... .

Considerando qualquer um desses pontos e o coeficiente angular igual a 1, podemos concluir que a reta que representa a bissetriz dos quadrantes ímpares terá - de acordo com os conceitos de Geometria Analítica - a equação fundamental: y – y0 = m (x – x0).
Substituindo o ponto (2,2), temos:

y – 2 = 1 (x – 2)
y – 2 = x – 2
y = x

Bissetriz dos quadrantes pares
A bissetriz dos quadrantes pares é determinada por uma reta que intercepta o ponto (0,0) traçando as bissetrizes dos quadrantes II e IV.



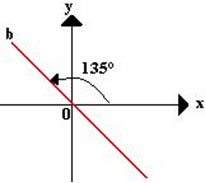
O coeficiente angular será igual a m = tg 135° = -1. Um dos seus pontos será (0,0) e todos os outros pontos pertencentes à reta b terão os valores das ordenadas opostos aos valores das abscissas, por exemplo, (4,-4), (5,-5), (6,-6), (7,-7),... .

Considerando qualquer um desses pontos e o coeficiente angular igual a -1, podemos concluir que a reta que representa a bissetriz dos quadrantes pares terá - de acordo com os conceitos de Geometria Analítica - a equação fundamental: y – y0 = m (x – x0).
y – (–2) = –1 (x – 2)
y + 2 = –x + 2
y = – x

Por Marcos Noé

Nùmeros Complexos

Conjunto dos Números Complexos aula 6

Área do retângulo

Retângulo

Existem dois tipos de retângulos: com lados todos iguais (quadrado) e com os lados diferentes.



No cálculo de qualquer retângulo podemos seguir o raciocínio abaixo:


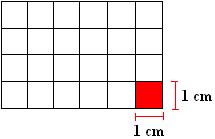
Pegamos um retângulo e colocamos em uma malha quadriculada onde cada quadrado tem dimensões de 1 cm. Se contarmos, veremos que há 24 quadrados de 1 cm de dimensões no retângulo. Como sabemos que a área é a medida da superfície de uma figuras podemos dizer que 24 quadrados de 1 cm de dimensões é a área do retângulo.



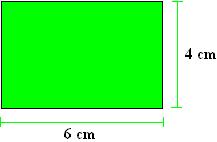
O retângulo acima tem as mesmas dimensões que o outro, só que representado de forma diferente. O cálculo da área do retângulo pode ficar também da seguinte forma:

A = 6 . 4
A = 24 cm²

Podemos concluir que a área de qualquer retângulo é:



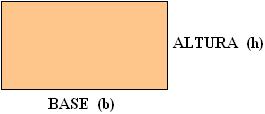
A = b . h


Quadrado
É um tipo de retângulo específico, pois tem todos os lados iguais. Sua área também é calculada com o produto da base pela altura. Mas podemos resumir essa fórmula:


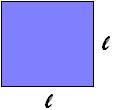
Como todos os lados são iguais, podemos dizer que base é igual a e a altura igual a 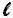, então, substituindo na fórmula A = b . h, temos:

A = .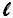
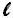
mundoeducacao