Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
As propriedades envolvendo determinantes facilitam o cálculo de seu valor em matrizes que se enquadram nessas condições. Observe as propriedades:
1ª propriedade
Ao observar uma matriz e verificar que os elementos de uma linha ou uma coluna são iguais a zero, o valor do seu determinante também será zero.

2ª propriedade
Caso ocorra igualdade de elementos entre duas linhas ou duas colunas, o determinante dessa matriz será nulo.
Caso ocorra igualdade de elementos entre duas linhas ou duas colunas, o determinante dessa matriz será nulo.

3ª propriedade
Verificadas em uma matriz duas linhas ou duas colunas com elementos de valores proporcionais, o determinante terá valor igual à zero. Observe a propriedade entre a 1ª e a 2ª linha.

4ª propriedade
Ao multiplicarmos todos os elementos de uma linha ou coluna de uma matriz por um número K, o seu determinante fica multiplicado por K.
Ao multiplicarmos todos os elementos de uma linha ou coluna de uma matriz por um número K, o seu determinante fica multiplicado por K.

Os elementos da 1ª linha de P foram multiplicados por 2, então: det P’ = 2 * det P
5ª propriedade
Caso uma matriz quadrada A seja multiplicada por um número real k, seu determinante passa a ser multiplicado por kn.
det (k*A) = kn * det A
6ª propriedade
O valor do determinante de uma matriz R é igual ao determinante da matriz da transposta de R, det R = det (Rt).
5ª propriedade
Caso uma matriz quadrada A seja multiplicada por um número real k, seu determinante passa a ser multiplicado por kn.
det (k*A) = kn * det A
6ª propriedade
O valor do determinante de uma matriz R é igual ao determinante da matriz da transposta de R, det R = det (Rt).
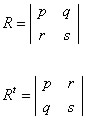
det R = ps -- qr
det Rt = ps – rq
7ª propriedade
Ao trocarmos duas linhas ou duas colunas de posição de uma matriz, o valor do seu determinante passa a ser oposto ao determinante da anterior.
8ª propriedade
O determinante de uma matriz triangular é igual à multiplicação dos elementos da diagonal principal.
Lembre-se que em uma matriz triangular, os elementos acima ou abaixo da diagonal principal são iguais a zero.
det Rt = ps – rq
7ª propriedade
Ao trocarmos duas linhas ou duas colunas de posição de uma matriz, o valor do seu determinante passa a ser oposto ao determinante da anterior.
8ª propriedade
O determinante de uma matriz triangular é igual à multiplicação dos elementos da diagonal principal.
Lembre-se que em uma matriz triangular, os elementos acima ou abaixo da diagonal principal são iguais a zero.

9ª propriedade
Considerando duas matrizes quadradas de ordem iguais e AB matriz produto, temos que: det (AB) = (det A) * (det B), conforme teorema de Binet.
10ª propriedade
Ao multiplicarmos todos os elementos de uma linha ou de uma coluna pelo mesmo número e adicionarmos os resultados aos elementos correspondentes de outra linha ou coluna, formamos a matriz B, onde ocorre a seguinte igualdade: det A = det B. Esse teorema é atribuído a Jacobi.
Por Marcos NoéConsiderando duas matrizes quadradas de ordem iguais e AB matriz produto, temos que: det (AB) = (det A) * (det B), conforme teorema de Binet.
10ª propriedade
Ao multiplicarmos todos os elementos de uma linha ou de uma coluna pelo mesmo número e adicionarmos os resultados aos elementos correspondentes de outra linha ou coluna, formamos a matriz B, onde ocorre a seguinte igualdade: det A = det B. Esse teorema é atribuído a Jacobi.
Graduado em Matemática
Nenhum comentário:
Postar um comentário