Operações com números complexos na forma algébrica
Marcelo Rigonatto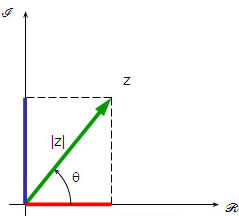
Representação gráfica de z
Considere dois números complexos z1 = a + bi e z2 = c + di. Vamos analisar como se dá cada uma das operações citadas para os elementos desse conjunto.
1. Adição
z1 + z2 = (a + bi) + (c + di) = (a + c) + (b + d)i
Observe que basta somar a parte real de um com a parte real do outro e proceder da mesma forma com a parte imaginária.
Exemplo: Dados os números complexos z1 = 5 + 8i, z2 = 1 + 2i e z3 = 2 – 3i, calcule:
a) z1 + z2 = (5 + 8i) + (1 + 2i) = (5 + 1) + (8 + 2)i = 6 + 10i
b) z2 + z3 = (1 + 2i) + (2 – 3i) = (1 + 2) + (2 – 3)i = 3 – i
2. Subtração
A subtração é feita de forma análoga. Observe:
z1 – z2 = (a + bi) – (c + di) = (a – c) + (b – d)i
Exemplo:
a) (5 + 8i) – (1 + 2i) = (5 – 1) + (8 – 2)i = 4 + 6i
b) (1 + 2i) – (2 – 3i) = (1 – 2) + [2 – (– 3)]i = – 1 + 5i
3. Multiplicação
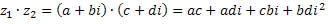
Como sabemos, i2 = – 1.
Logo,
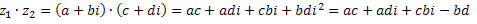
Agrupando os termos semelhantes, obtemos:
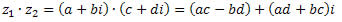
Exemplo:
a) (5+8i)∙(1+2i) = (5∙1-8∙2)+(5∙2+1∙8)i
(5+8i)∙(1+2i) = (5-16) + (10+8)i = -11+18i
b) (1+2i)∙(2-3i) = [1∙2 - 2∙(-3)] + [1∙(-3) + 2∙2]i
(1+2i)∙(2-3i) = (2+6) + (-3+4)i = 8 + i
4. Divisão
Para realizar a divisão de dois números complexos precisamos introduzir o conceito de conjugado de um número complexo. Seja z = a + bi, o conjugado de z é z̅ = a - bi. Agora podemos definir a operação de divisão para números complexos.
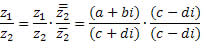
Exemplo:
a)

Vamos fazer os cálculos do numerador e do denominador separadamente:
(5 + 8i)(1 - 2i) = [5∙1 - 8(-2)] + [5∙(-2) + 1∙8]i = 21 - 2i
Na multiplicação dos denominadores basta aplicar a seguinte propriedade:
z ∙ z̅ = (a + bi) (a - bi) = a2 + b2
Assim,
(1 + 2i)(1 - 2i) = 12 + 22 = 5
Logo,
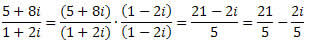
b)
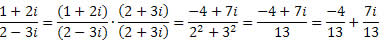
Nenhum comentário:
Postar um comentário