Princípio Fundamental da Contagem

Professor de Matemática no Colégio Estadual Dinah Gonçalves

E Biologia na rede privada de Salvador-Bahia

Professor Antonio Carlos carneiro Barroso

email accbarroso@hotmail.com

Blog HTTP://ensinodematemtica.blogspot.com e HTTP://accbarroso60.wordpress.com

Extraído de http://www.alunosonline.com.br

Princípio Fundamental da Contagem

Marcos Noé

Princípio da contagem nas placas de automóveis

O princípio fundamental da contagem está diretamente ligado às situações que envolvem as possibilidades de um determinado evento ocorrer, por exemplo, os modos distintos que podemos organizar as pessoas em uma fila, o número de placas de automóveis que podemos formar com letras e algarismos, as possíveis combinações da Mega Sena, entre outras situações. O princípio fundamental da contagem é a estrutura básica da Análise Combinatória, através dele desenvolvemos técnicas e métodos de contagem na resolução direta de problemas.

Exemplo 1

Vamos supor que uma fábrica produza motos de tamanhos grande, médio e pequeno, com motores de 125 ou 250 cilindradas de potência. O cliente ainda pode escolher as seguintes cores: preto, vermelha e prata. Quais são as possibilidades de venda que a empresa pode oferecer?

Vamos construir uma árvore de possibilidades:

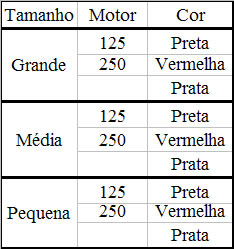
Possibilidades de venda

Grande – 125 cc – preta
Grande – 125 cc – vermelha
Grande – 125 cc – prata
Grande – 250 cc – preta
Grande – 250 cc – vermelha
Grande – 250 cc – prata

Média – 125 cc – preta
Média – 125 cc – vermelha
Média – 125 cc – prata
Média – 250 cc – preta
Média – 250 cc – vermelha
Média – 250 cc – prata

Pequena – 125 cc – preta
Pequena – 125 cc – vermelha
Pequena – 125 cc – prata
Pequena – 250 cc – preta
Pequena – 250 cc – vermelha
Pequena – 250 cc – prata

O número de possibilidades de venda totaliza 18 opções.

A fábrica oferece três tamanhos de moto, e para cada tamanho dois tipos de motores e, ainda, três opções de cores. Dessa forma, o número total de possibilidades resulta da seguinte multiplicação: 3 * 2 * 3 = 18 possibilidades. Esse cálculo efetuado de forma direta é denominado Regra do Produto.

Exemplo 2

De quantas maneiras distintas podemos formar placas de automóveis, com 3 letras e 4 algarismos? Considere as letras do alfabeto e os algarismos de 0 a 9.

A formatação da placa será a seguinte:

Considerando as 26 letras do alfabeto e os algarismos de 0 a 9, teremos:

Aplicando a regra do produto, temos:

26 * 26 * 26 * 10 * 10 * 10 * 10 = 175 760 000 placas.