Mostrando postagens com marcador 9º Ano. Mostrar todas as postagens
Mostrando postagens com marcador 9º Ano. Mostrar todas as postagens

sexta-feira, 3 de setembro de 2021

Equação Biquadrada.

Exercícios Propostos - Equação Biquadrada.






/www.matematicamuitofacil.com
Posted by on Nenhum comentário:
Marcadores:

Escalas termométricas

Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
       


Escala Fahrenheit

A Escala Fahrenheit foi construída, em 1727, pelo físico alemão Daniel Gabriel Fahrenheit, que adotou o valor 0 (zero) para a mistura: água, gelo picado e sal; e o valor 100 para a temperatura do corpo humano. Dividiu-se o intervalo entre esses pontos fixos em 100 partes iguais e cada parte recebeu o nome de grau Fahrenheit, cujo símbolo é °F.
Ao compararmos os pontos fixos escolhidos por Fahrenheit e Celsius, temos para o ponto de fusão do gelo, sob pressão de 1 atmosfera, o valor 32 °F e para o ponto de vapor da água, também sob pressão de 1 atmosfera, o valor 212 °F; o intervalo dividido em 100 partes iguais pelo sueco (Celsius) é dividido em 180 partes iguais na escala Fahrenheit.

Escala Fahrenheit

Escala Kelvin

Como a temperatura de um corpo está relacionada com o grau de agitação de suas moléculas, podemos dizer que as escalas Celsius e Fahrenheit são relativas, uma vez que elas não atribuem o valor zero ao estado de agitação molecular mais baixo.
A temperatura está relacionada à energia de movimento das moléculas de um corpo; assim, ao diminuirmos sua temperatura, suas moléculas ficam mais lentas. Podemos imaginar um estado em que todas as moléculas estão paradas, ou seja, agitação térmica nula correspondendo à temperatura zero, a qual denominamos zero absoluto.
O físico irlandês, Willian Thomson, que recebeu o título de nobreza lorde Kelvin, estabeleceu, em 1848, uma escala absoluta, a chamada Escala Kelvin.
Kelvin verificou experimentalmente que a pressão de um gás diminuía 1/273 do valor inicial, quando resfriado a volume constante de 0 °C para – 1 °C. Como a pressão do gás está relacionada com o choque de suas partículas com as paredes do recipiente, quando a pressão fosse nula, as moléculas estariam em repouso, a agitação térmica seria nula e a sua temperatura também. Conclui, entáo, que isso aconteceria se transformássemos o gás até – 273 °C.
Assim, Kelvin atribuiu o valor zero para este estado térmico e o valor de 1 kelvin a uma extensão igual à do grau Celsius, de modo que o ponto de fusão do gelo corresponde a 273 K e o ponto de ebulição da água corresponde a 373 K (o nome e o símbolo grau kelvin foram abolidos em convenção científica internacional e substituídos simplesmente por kelvin; portanto, ao invés de 10 °K, escreve-se 10 K e lê-se: dez kelvin).
Posteriormente, descobriu-se impossível atingir o estado de agitação molecular nulo; as moléculas têm uma energia mínima denominada energia do ponto zero e o zero absoluto é inatingível na prática. O zero absoluto é obtido por extrapolação e não deve ser interpretado como o estado em que as partículas estariam em completo repouso, pois elas possuem uma energia mínima finita e apresentam movimento.

Escala Celsius

A Escala Celsius construída em 1742, pelo físico e astrônomo sueco Anders Celsius, que adotou para o ponto de fusão de gelo o valor 0 (zero) e para o ponto de ebulição da água o valor 100 (cem). Dividiu-se o intervalo obtido entre os pontos fixos em cem partes iguais, em que cada parte corresponde à uma unidade da escala e foi denominada de grau Celsius, cujo símbolo é o °C.

Escala Celsius

Como o intervalo entre os pontos fixos dessa escala foi dividido em cem partes iguais, ela recebeu o nome de escala centígrada ou centesimal e, atualmente, a escala Celsius é a mais utilizada em todo o mundo.

Conversão de unidades: Kelvin Celsius Fahrenheit

Como existem várias escalas termométricas, freqüentemente necessitamos transformar a indicação numérica de uma escala em outra. Em provas de vestibular, este tipo de questão é bastante frequente. Para obtermos a relação entre uma escala e outra, devemos estabelecer a proporção entre os segmentos obtidos com a leitura da temperatura de um corpo com dois termômetros. Por exemplo, ao medirmos a temperatura de um corpo com tres termômetros, um graduado na escala Celsius, outro na escala Fahrenheit e um terceiro na escala Kelvin, obtemos os segmentos a e b (figura a seguir) da coluna de mercúrio que corresponde ao mesmo estado térmico e não dependem da unidade em que foram medidos.
Portanto:
Conversão unidades: Kelvin Celsius Fahrenheit
Conversão unidades: Kelvin Celsius Fahrenheit

Entre as escalas Celsius e Fahrenheit, podemos simplificar para:

Conversão unidades: Kelvin Celsius Fahrenheit

Esta relação recebe o nome de equação termométrica, e, dessa forma, podemos estabelecer equações de conversão entre quaisquer escalas termométricas, sejam elas relativas, arbitrárias ou mesmo absolutas.
Observe, através da equação termométrica de conversão entre as escalas Celsius e Fahrenheit, que as equações termométricas são funções do primeiro grau, e, se as representarmos em um diagrama, obteremos uma reta, conforme figura abaixo.
Conversão unidades: Kelvin Celsius Fahrenheit

1. Variação de Temperatura
Considere que a temperatura de um corpo varie de um valor inicial T1 para um valor final T2, num dado intervalo de tempo. A variação de temperatura T é dada pela diferença entre o final T2 e o valor inicial T1:

Conversão unidades: Kelvin Celsius Fahrenheit

Por exemplo, relacionando as variações de temperatura nas três escalas Celsius, Fahrenheit e Kelvin temos:
• o segmento a, que corresponde à variação de temperatura ocorrida nas três escalas, e o segmento b, que corresponde ao intervalo de temperatura entre os pontos de vapor e de gelo, também nas suas escalas. Como eles não dependem da unidade em que foram medidos, podemos estabelecer a proporção:

Conversão unidades: Kelvin Celsius Fahrenheit
Conversão unidades: Kelvin Celsius Fahrenheit

Simplificando:

Conversão unidades: Kelvin Celsius Fahrenheit

www.vestibulandoweb.com.br

Posted by on Nenhum comentário:
Marcadores: , ,

Área do setor circular

Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com          
      

Área do setor circular

Marcelo Rigonatto


Setor circular
Sabemos que a área de uma circunferência é diretamente proporcional ao tamanho do seu raio e é obtida fazendo π∙r2, onde π equivale, aproximadamente, 3,14. O setor circular é uma parte da circunferência limitada por dois raios e um arco central. A determinação da área do setor circular depende da medida desse ângulo central e do comprimento do raio da circunferência.
Como uma volta completa na circunferência equivale a 360o, podemos pensar da seguinte maneira para obter uma fórmula para calcular a área do setor circular:

360o -------------- π∙r2
α ------------------ Asetor

Assim, teremos:
Onde,
α → é o ângulo central do setor circular.
r → é o raio da circunferência.

Vejamos alguns exemplos.

Exemplo 1. Determine a área do setor circular abaixo. (Use π = 3,14)


Solução: Como conhecemos o raio e a medida do ângulo central, basta substituir esses valores na fórmula da área do setor circular.

Exemplo 2. Numa circunferência de área igual a 121π cm2, calcule a área do setor circular delimitado por um ângulo central de 120o.

Solução: Para solução desse problema devemos verificar que no numerador da fórmula da área do setor circular, a medida do ângulo central α está multiplicando a área da circunferência, dessa forma teremos:

Posted by on Nenhum comentário:
Marcadores: ,

Radical duplo na soma de dois simples.

Na obra de Sebastião e Silva incluem-se livros escolares do liceu: de Matemática “clássica”, os Compêndios de Álgebra para o 6.º e 7.º anos (em colaboração com J. da Silva Paulo),  Geometria Analítica,  para o 7.º ano; de Matemática “moderna”,  o Compêndio de Matemática I, II e III e respectivos Guias (Texto-piloto segundo o projecto executado pelo Ministério da Educação Nacional em cooperação com a O.C.D.E.).
Estes últimos serviram para apoiar os professores e alunos das turmas piloto que seguiram, em finais de 1960 e princípios de 1970,  um programa inovador, por ele concebido, considerado de nível internacional.
Eu segui o programa antigo e só contactei com o primeiro livro de Sebastião e Silva de Matemática “moderna”, já no início do meu primeiro ano do Técnico, para aprender melhor uma breve introdução à Lógica que iniciava as Matemáticas Gerais, em 68/69, do Prof. Campos Ferreira, um dos seus seguidores.
Sempre achei a exposição dos seus livros excelente e, ao mesmo tempo, cativadora e rigorosa. Foi à Álgebra do meu 7.º ano (pp.141-144) que recorri para relembrar uma transformação de um radical duplo na soma de dois simples, que é enunciada sob a forma do seguinte problema:
« Dados dois números racionais positivos A e B, não sendo B um quadrado perfeito, determinar dois números racionais positivos x e y tais que
\sqrt{A\pm\sqrt{B}}=\sqrt{x}\pm\sqrt{y}
Comecemos pelo caso
\sqrt{A+\sqrt{B}}=\sqrt{x}+\sqrt{y}
(…)
Esses números [x e y] são (…) as raízes da equação
X^2-AX+\dfrac{B}{4}=0
as quais são dadas pelas expressões:
\dfrac{A+\sqrt{A^2-B}}{2}\qquad\text{e}\qquad\dfrac{A-\sqrt{A^2-B}}{2}.
Podemos agora escolher um destes dois valores para x; o outro será o correspondente valor de y. Como x e y devem ser racionais , sem o que a decomposição , que se pretende, deixa de existir, é necessário que A^2-B seja um quadrado perfeito. (…) se pusermos \sqrt{A^2-B}=C, será C um número racional e o mesmo se poderá dizer dos números
\dfrac{A+C}{2}\qquad\text{e}\qquad\dfrac{A-C}{2}
que são as soluções da equação. (…)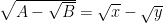
Consideremos agora o caso  
\sqrt{A-\sqrt{B}}=\sqrt{x}-\sqrt{y}
(…) O valor de x deverá, aqui, ser \dfrac{A+C}{2} para que a diferença
\sqrt{x}-\sqrt{y}=\sqrt{\dfrac{A+C}{2}}-\sqrt{\dfrac{A-C}{2}}
resulte positiva, visto ser positivo o radical \sqrt{A-\sqrt{B}} que lhe é igual.  »
Este resultado permitiu-me facilmente chegar à solução do problema publicado nesta minha entrada, como expliquei aqui.
Actualização de 20-12-2009: acrescentada figura do livro e referidas as páginas onde a transformação é tratada.
Adenda de 23-5-2011: Em comentário abaixo andreelopess indica a sequinte igualdade 
\dfrac{3}{\sqrt{7-2\sqrt{10}}}+\dfrac{4}{\sqrt{8+4\sqrt{3}}}=\dfrac{1}{\sqrt{11-2\sqrt{30}}}\qquad (\ast)
que, por racionalização de denominadores, se transforma em
\sqrt{7+2\sqrt{10}}+\sqrt{8-4\sqrt{3}}=\sqrt{11+2\sqrt{30}}\qquad (\ast\ast)
Aplicando o método exposto conclui-se que
\sqrt{7+2\sqrt{10}}=\sqrt{5}+\sqrt{2}
\sqrt{8-4\sqrt{3}}=\sqrt{6}-\sqrt{2}
\sqrt{11+2\sqrt{30}}=\sqrt{6}+\sqrt{5}
pelo que efectivamente se tem (\ast\ast). Depois de cálculos fastidiosos concluo  ser equivalente a
\left( 2+\sqrt{2}\sqrt{5}+2\sqrt{14-7\sqrt{3}+4\sqrt{2}\sqrt{5}-2\sqrt{3}\sqrt{2}\sqrt{5}}-2\sqrt{3}\right) ^{2}=30
que confrontei com o resultado em Wolfram Alpha: aqui
Adenda de 24-5-2011: Como escrevo em baixo Sem utilizar o método exposto no post é fácil não digo encontrar, mas justificar as relações numéricas, depois de conhecida a decomposição. Basta elevar ao quadrado ambos os membros.
Fonte:problemasteoremas.wordpress.com
Posted by on Nenhum comentário:
Marcadores:
Assinar: Postagens (Atom)