Cálculo de Derivadas

Obs.: f é uma função, f' é a sua derivada.
==> Derivadas:
*Função Constante:
f'( c ) = 0;
Exemplo: f'(5) = 0;
*Função Identidade:
f'(x) = 1;
Exemplo: f'(2x) = 2.1 = 2; (Quando se tem uma constante no termo, ela permanece. No caso de uma constante estar sozinha num termo, a sua derivada vale zero.
*Função Exponencial Natural:
f'(e^x) = (e^x) . x';
Exemplo: f'(e^2x) = (e^2x) . 2 = 2e^2x; (O símbolo ^ significa "elevado à")
*Função Logaritmo natural:
f'(ln|x|) = x'/x;
Exemplo: f'(ln|2x+1|) = 2/2x+1;
*Derivada da soma de duas funções:
f'(g(x)+h(x)) = f'(g(x)) + f'(h(x));
Exemplo: f'((2x) + (5x^2+5)) = 2 + 10x;
*Derivada do produto de uma constante por uma função:
f'(c.g(x)) = c.g'(x);
Exemplo: f'(2.(2x)) = 2.2 = 4;
*Função potência:
f'(x^n) = n.x^(n-1);
Exemplo: f'(x^3) = 3x^2;
*Derivada do produto de duas funções:
f'(g(x) . h(x)) = g'(g).h(x) + g(g).h'(x);
Exemplo: f'(3x^2 . 5x) = 6x.5x + (3x^2).5 = 30x^2 + 15x^2 = 45x^2;

Derivadas

Derivadas I

Derivada de uma função y = f(x) num ponto x = x0

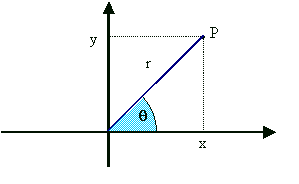
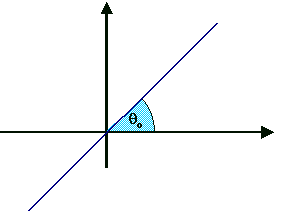
Considere a figura abaixo, que representa o gráfico de uma função y = f(x), definida num intervalo de números reais.

Observando a figura, podemos definir o seguinte quociente, denominado razão incremental da função
y = f(x), quando x varia de x0 para x0 + D x0 :

Define-se a derivada da função y = f(x) no ponto x = x0, como sendo o limite da razão incremental acima, quando D x0 tende a zero, e é representada por f ' (x0) , ou seja:

Nota: a derivada de uma função y = f(x), pode ser representada também pelos símbolos y ' ou dy/dx.

Observe que quando D x0 ® 0 , o ponto Q no gráfico acima, tende a coincidir com o ponto P da mesma figura., definindo a reta r , que forma um ângulo b com o eixo horizontal (eixo das abcissas), e, neste caso, o ângulo SPQ = a .tende ao valor do ângulo b .
Ora, quando D x0 ® 0 , já vimos que o quociente D y0 / D x0 representa a derivada da função y = f(x)
no ponto x0. Mas, o quociente D y0 / D x0 representa , como sabemos da Trigonometria, a tangente do ângulo
SPQ = a , onde P é o vértice do ângulo. Quando D x0 ® 0 , o ângulo SPQ = a , tende ao ângulo b .

Assim, não é difícil concluir que a derivada da função y = f(x) no ponto x = x0 , é igual numericamente à tangente do ângulo b . Esta conclusão será muito utilizada no futuro.

Podemos escrever então:
f '(x0) = tgb

Guarde então a seguinte conclusão importante:

A derivada de uma função y = f(x) num ponto x = x0 , coincide numericamente com o valor da tangente trigonométrica do ângulo formado pela tangente geométrica à curva representativa de y = f(x), no ponto
x = x0.

Estou falando há muito tempo em DERIVADAS, e ainda não calculei nenhuma!

Vamos lá!

Existem fórmulas para o cálculo das derivadas das funções - as quais serão mostradas no decorrer deste curso - mas, por enquanto, vamos calcular a derivada de uma função simples, usando a definição. Isto servirá como um ótimo exercício introdutório, que auxiliará no entendimento pleno da definição acima.

Calcule a derivada da função y = x2 , no ponto x = 10.

Temos neste caso:
y = f(x) = x2
f(x + D x) = (x + D x)2 = x2 + 2x.D x + (D x)2
f(x + D x) - f(x) = x2 + 2x.D x + (D x)2 - x2 = 2x.D x + (D x)2
D y = f(x + D x) - f(x) = x2 + 2x.D x + (D x)2 - x2 = 2x.D x + (D x)2

Portanto,

Observe que colocamos na expressão acima, D x em evidencia e, simplificamos o resultado obtido.
Portanto a derivada da função y = x2 é igual a y ' = 2x .
Logo, a derivada da função y = x2, no ponto x = 10 , será igual a : y ' (10) = 2.10 = 20.

Qual a interpretação geométrica do resultado acima?

Ora, a derivada da função y = x2 , no ponto de abcissa x = 10 , sendo igual a 20, significa que a tangente trigonométrica da reta tangente à curva y = x2 , no ponto x = 10 , será também igual a 20 , conforme teoria vista acima.

Ora, sendo b o ângulo formado por esta reta tangente com o eixo dos x , b será um ângulo tal que tg b = 20. Consultando uma tábua trigonométrica OU através de uma calculadora científica, concluímos que
b » 87º 8' 15" .

Então, isto significa que a reta tangente à curva de equação y = x2 , no ponto de abcissa x = 10, forma com o eixo dos x um ângulo igual aproximadamente a b » 87º 8' 15" .

Agora, calcule como exercício inicial, usando a definição, a derivada da função y = 5x no ponto de abcissa
x = 1000 .
Resposta: 5.



Derivadas II

1 - Vimos na apostila (derivadas I) anterior, que a derivada de uma função y = f(x) no ponto x = x0 pode ser determinada, calculando-se o limite seguinte:

Onde:

A rigor, para o cálculo da derivada de uma função, teremos que calcular o limite acima, para cada função dada. É entretanto, de bom alvitre, conhecer de memória as derivadas das principais funções. Não estamos aqui, a fazer a apologia do "decoreba" , termo vulgarmente utilizado para a necessidade de memorização de uma fórmula. Achamos entretanto, que, por aspectos de praticidade, o conhecimento das fórmulas de derivação de funções, seja de extrema importância, sem, entretanto, eliminar a necessidade de saber
deduzi-las, quando necessário.

Assim, lembrando que a derivada de uma função y = f(x) pode ser indicada pelos símbolos
y ' , f ' (x) ou dy/dx , apresentaremos a seguir, uma tabela contendo as derivadas de algumas das principais funções elementares, restringindo nesta primeira abordagem, a oito funções elementares básicas, além das derivadas da soma, produto e quociente de duas funções.

FUNÇÃO


DERIVADA

y = k , k = constante


y ' = 0

y = k.x


y ' = k

y = x


y' = 1

y = xn


y ' = n.x n - 1

y = a x , 1 ¹ a > 0


y ' = a x . ln a

y = e x


y ' = e x

y = sen(x)


y ' = cos(x)

y = cos(x)


y ' = - sen(x)

y = tg(x)


y ' = sec2 (x)

y = u + v


y ' = u' + v'

y = u.v


y' = u'.v + u.v'

y = u / v , v ¹ 0


y' = (u'.v - u.v') / v2

Onde u = u(x) e v = v(x) são funções deriváveis no ponto x.

Tenham calma, que esta tabela será devidamente ampliada, no devido tempo. Estou partindo da premissa, que a introdução a um assunto novo, tem necessariamente que ser de forma lenta e gradual. Sem pressa!

a) y = 1000 Þ y ' = 0
b) y = 200x Þ y ' = 200
c) y = x5 Þ y ' = 5x4
d) y = x + sen(x) Þ y ' = x ' + (senx) ' = 1 + cos(x)
e) y = x3 + x2 Þ y ' = 3x2 + 2x
f) y = sen(x) + cos(x) Þ y ' = cos(x) - sen(x)
g) y = 1 / x Þ y ' = (1'.x - 1. x') / x2 = - 1 / x2
h) y = x.sen(x) Þ y ' = x'. sen(x) + x . (senx)' = sen(x) + x.cos(x)
i) y = x + tg(x) Þ y ' = 1 + sec2 (x)

Agora determine a derivada da função y = x2.tg(x).
Resposta: y ' = 2.x.tg(x) + [x.sec(x)]2

2 - Equação da reta tangente à curva representativa da função y = f(x) no ponto x = x0

Considere a figura abaixo:

Seja determinar a equação da reta r tangente à curva y = f(x), no ponto x = x0.
Já sabemos da aula anterior , que tg b = f '(x0) , onde b é o ângulo formado pela reta r com o eixo dos x e
f '(x0) é o valor da derivada da função y = f(x) no ponto de abcissa x = x0.
Também já sabemos da Geometria Analítica que o valor da tg b é igual ao coeficiente angular m da reta r , ou seja: m = tg b . Como já sabemos da Analítica que a equação da reta r, é y - y0 = m(x - x0) , vem imediatamente que a equação da reta tangente procurada será então dada por:
y - y0 = f '(x0) (x - x0)




Exemplo:



Qual a equação da reta tangente à curva representativa da função
y = f(x) = 4x3 + 3x2 + x + 5, no ponto de abcissa x = 0 ?

Ora, f '(x) = 12x2 + 6x + 1.
Portanto, a derivada no ponto de abcissa x = 0, será: f '(0) = 12.02 + 6.0 + 1 = 1
Logo, f ' (0) = 1.
Portanto, para achar a equação da reta tangente no ponto de abcissa x = 0, basta agora, determinar o valor correspondente de y da função, para x = 0.

Teremos: x = 0 Þ y = f(0) = 4.03 + 3.02 + 6.0 + 5 = 5
Então, o ponto de tangência é o ponto P(0, 5). Daí, vem finalmente que:
y - 5 = 1 . (x - 0) \ y - 5 = x \ y = x + 5 .

Resposta: a equação da reta tangente à curva y = 4x3 + 3x2 + 6x + 5 , no ponto P(0,5) , é y = x + 5.

Agora resolva este:

Determinar a equação da reta tangente à curva representativa da função y = x3 ,
no ponto P de abcissa x = 2.

Resposta: y = 12x - 16.
www.coladaweb.com

Limites Continuidades da função aula 4

Cálculo de áreas de figuras planas – (coordenadas polares)

Introdução

Como foi visto na Matemática Básica, as coordenadas polares são usadas para representar pontos de um plano.

Para definir um sistema de coordenadas polares, consideramos um ponto O do plano (chamado origem ou pólo) e uma semi-reta orientada com extremidade O ( o eixo polar). Dado um ponto P ¹O do plano tomamos,

q , uma ângulo formado pelo eixo polar e OP, tendo origem no eixo polar, positivo se orientado no sentido anti-horário e negativo se no sentido horário.
r, a distância de P a O
r e q são coordenadas polares de P e representamos P = (r, q )

Dado um ponto qualquer do plano, as suas coordenadas polares não são únicas.

Exemplo 1: Representar graficamente os pontos de coordenadas polares

Como estes ângulos são côngruos temos P₁ = P₂ = P₃

As coordenadas do pólo são (0, q ) para todo q Î R .

Tomamos também valores negativos para a coordenada r. Se r é negativo, o ponto de coordenadas polares (r, q ) é tal que (-r, q + p ) são também coordenadas deste ponto

Exemplo 2: Representar graficamente o ponto de coordenadas polares

Suponhamos neste mesmo plano um par de eixos cartesianos XOY de modo que o semi-eixo OX positivo coincida com o eixo polar.
Se P é um ponto qualquer do plano de coordenadas polares (r, q ) e coordenadas cartesianas (x ,y) então

x = r.cos(q )

y = r.sen(q )

x2 + y2 = r2

Exemplo 3: Consideremos as curvas a seguir e suas equações em coordenadas polares

3.1) O círculo da raio r_o e centro na origem tem equação polar r = r_o

3.2) A reta que passa pela origem e faz um ângulo q _o com o sentido positivo do eixo OX tem equação polar q = q _o

Voltar ao ÍndiceÁrea de um setor circular

A área de um setor circular de raio r e ângulo central q é igual a

Proposição 1: Seja a equação polar de uma curva dada pela função contínua  r = r (q )  para a   £  q   £ b   tal   que  b  -  a   £  2p  e   r ³ 0. A área da região do plano limitada  pelas   retas  de equações  polares  q = a e q = b e a curva r = r(q ) é igual a.

Demonstração.

Para todo q tal que a £ q £ b , seja A(q ) a área como indicada na figura abaixo.

Vamos calcular

Para D q > 0 , tomando-se no intervalo [ q , q + D q ], r_M e r_m o maior e o menor raio, as áreas dos setores circulares com ângulo central D q e esses raios são

Para D q < 0 segue de modo análogo.
Pelo teorema fundamental do cálculo

Voltar ao Índice

Exemplo 4: Calcular a área limitada pela cardióide r (q ) = a.(1 – cos(q ))

Observação 1: São equações de cardióides:

r (q ) = a.(1 ± cos(q )) e r (q ) = a.(1 ± sen(q ))

Exemplo 5: Calcular a área limitada pelas pétalas da rosácea r = a.sen(2q ), a > 0
Trata-se de uma rosácea de 4 pétalas. Devido a simetria das pétalas, basta calcular a área de uma delas e multiplicar por 4.

Observação 2: São equações de rosáceas:

r = a.cos(nq )  e  r = a. sen(nq ), para n =1, 2, 3..., que possuem

• 2n pétalas , se n é par
• n pétalas se n é ímpar

Exemplo 6: Calcular a área limitada pela lemniscata r2 = 4.cos(2q ).
Como q deve ser tal que cos(2q ) >0, então, na 1a volta,
Devido a simetria dos semi-laços, basta  cal cular a área de um deles e multiplicar por 4.

Observação 3: São equações de lemniscatas:

r² = a.cos(2q ) e r² = a. sen(2q )

Exemplo 7: Calcular a área entre a 1a e a 2a volta da espiral (exponencial) r = eq , com 0 £ q .

Exemplo 8: Esboce a limaçon (com laço) de equação polar r = a.(1 – 2sen(q )) e determine uma expressão em integrais que represente a área da região do plano que se encontra no interior da curva e fora do laço.

Observação 4: São equações de limaçons:

r = a ± b.cos(q ) e r = a ± b.sen(q ) que possuem laço se a < b

Exemplo 9: Determine uma expressão em integrais que represente a área da região do plano sombreada na figura ao lado onde temos o arco da espiral de Arquimedes de equação polar r = q ; -p £ q £ p .

Exemplo 10: Determine uma expressão em integrais que represente a área da região do plano interior a ambas as curvas de equações polares r =1 + cos( q ) e r = 3cos( q )
r =1 + cos( q ) é equação de uma cardióide e r = 3cos( q ) é equação de um círculo.
Obtendo a interseção das duas curvas : 3cos( q ) = 1 + cos( q ) Þ cos( q ) = 1/2 Þ q = ± p /3 + 2kp

fonte :http://www.mat.ufba.br/