Esse é o blog do Professor de Matemática Carlos Barroso. Trabalho no Colégio Estadual Dinah Gonçalves . Valéria-Salvador-Bahia .Inscreva-se Já no meu canal www.youtube.com/accbarroso1 e receba as videoaulas de Matemática.
terça-feira, 5 de novembro de 2019
UAB oferta 81 mil vagas em nova Universidade do Professor
O sistema Universidade Aberta do Brasil (UAB)
será o principal responsável por ofertar vagas na nova iniciativa do
Ministério da Educação (MEC) para a formação de professores efetivos da
rede pública que não atuam em sua área de formação, a Rede Universidade
do Professor. São 105 mil vagas para o segundo semestre de 2016 nas
instituições federais de educação, sendo 81 mil na modalidade educação a
distância, por meio da UAB, e 24 mil vagas presenciais remanescentes.
Baseado em informações do Censo Escolar
2015, Mercadante destacou que, entre os 709.546 professores efetivos que
lecionam nos anos finais do ensino fundamental e no ensino médio,
334.717 têm a formação para a disciplina que ensinam em sala de aula,
enquanto 374.829 precisam complementar a formação superior. Estes casos
representam docentes que não têm a licenciatura nas disciplinas que
aplicam ou não têm o grau de bacharel na área.
Mercadante afirmou que a prioridade é a
formação de professores efetivos da rede pública na área em que já estão
atuando. “Não há como melhorar a qualidade da educação no Brasil se nós
não resolvermos esta questão da formação. O que mais vai motivar é se a
carreira docente valorizar esta formação específica”, disse o ministro.
“Este é o ponto mais estratégico para melhorar a qualidade da
educação”, concluiu.
Parfor Presencial
Além das vagas pelo sistema UAB e das vagas presenciais remanescentes, os professores também poderão optar pelo Plano Nacional de Formação de Professores (Parfor Presencial) que oferecerá, durante as férias escolares, cursos presenciais intensivos para docentes da rede pública de educação básica. As vagas serão oferecidas no primeiro semestre de 2017.
Além das vagas pelo sistema UAB e das vagas presenciais remanescentes, os professores também poderão optar pelo Plano Nacional de Formação de Professores (Parfor Presencial) que oferecerá, durante as férias escolares, cursos presenciais intensivos para docentes da rede pública de educação básica. As vagas serão oferecidas no primeiro semestre de 2017.
UAB
Criada em 2005, o sistema Universidade Aberta do Brasil (UAB) é um sistema integrado por universidades públicas que oferece cursos de nível superior para camadas da população que têm dificuldade de acesso à formação universitária, por meio do uso da metodologia da educação a distância. O público em geral é atendido, mas os professores que atuam na educação básica têm prioridade de formação, seguidos dos dirigentes, gestores e trabalhadores em educação básica dos estados, municípios e do Distrito Federal. Hoje, o Sistema é coordenado pela Diretoria de Educação a Distância (DED) da Capes.
Criada em 2005, o sistema Universidade Aberta do Brasil (UAB) é um sistema integrado por universidades públicas que oferece cursos de nível superior para camadas da população que têm dificuldade de acesso à formação universitária, por meio do uso da metodologia da educação a distância. O público em geral é atendido, mas os professores que atuam na educação básica têm prioridade de formação, seguidos dos dirigentes, gestores e trabalhadores em educação básica dos estados, municípios e do Distrito Federal. Hoje, o Sistema é coordenado pela Diretoria de Educação a Distância (DED) da Capes.
Pelo sistema UAB são ofertados os seis
mestrados no formato semi presencial do país: o Programa de Mestrado
Profissional em Matemática em Rede Nacional (Profmat), criado em 2010; o Programa de Mestrado Profissional em Letras (Profletras) e o Programa de Mestrado Nacional Profissional em Ensino de Física – MNPEF (ProFis), lançados em 2013; e os Programas de Mestrado Profissional em Rede Nacional em Artes (ProfArtes), Administração Pública (ProfiAP) e Ensino de História (ProfHistória).
Mais detalhes no link que segue destacado: Plano nacional de formação de professores da educação básica
segunda-feira, 4 de novembro de 2019
Sergipe

Bandeira de Sergipe
Significado da bandeira: as cores representam a integração do estado ao Brasil. As cinco estrelas brancas simbolizam os principais rios de Sergipe: São Francisco, Vaza-Barris, Sergipe, Cotinguiba e Poxim.
Com extensão territorial de aproximadamente 21,9 mil quilômetros quadrados, Sergipe é o menor estado brasileiro. Essa unidade federativa integra a Região Nordeste, e limita-se ao norte com Alagoas; e a oeste e ao sul com a Bahia; além de ser banhado a leste pelo Oceano Atlântico.
Conforme dados divulgados em 2010 pelo Instituto Brasileiro de Geografia e Estatística (IBGE), a população estadual é de 2.068.031 habitantes, sendo a densidade demográfica de 94,3 habitantes por quilômetro quadrado. São 75 municípios em Sergipe, cuja capital é a cidade de Aracaju.
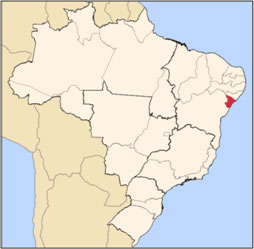
Localização de Sergipe no mapa do Brasil
O clima varia conforme a localidade: tropical atlântico no litoral e semiárido no interior. A caatinga é o bioma predominante, mas também há áreas de floresta tropical e mangues. O relevo é caracterizado por depressão e planície litorânea. A hidrografia, como já dito, é composta pelos rios São Francisco, Vaza-Barris, Jarapatuba, Real, Sergipe, Cotinguiba, Poxim, entre outros.
Na economia, Sergipe teve a cana-de-açúcar como principal produto durante décadas. No entanto, a partir da década de 1990, houve um considerável processo de industrialização. A indústria atua na produção de alimentos, couro, petroquímico, mobiliário, etc. A agricultura baseia-se nos cultivos de mandioca, milho, feijão e cana-de-açúcar. O turismo também é uma importante fonte de capitação de recursos financeiros.
Com relação aos aspectos sociais, o estado apresenta uma alta taxa de mortalidade infantil – 31,4 óbitos a cada mil nascidos vivos. Outro problema é o analfabetismo, que atinge 16,3% dos habitantes.
alunosonline
Pernambuco
Pernambuco

Bandeira de Pernambuco
Significado da bandeira: a cor azul representa o céu de Pernambuco; o branco, a paz. A cruz vermelha simboliza a fé na justiça e no entendimento; a estrela, o estado; o arco-íris, a união de todos os cidadãos pernambucanos; e o sol, a força e a energia do estado.
Pernambuco é um estado brasileiro que integra a Região Nordeste do país. Sua área, banhada a leste pelo Oceano Atlântico, limita-se com Alagoas, Bahia, Piauí, Ceará e Paraíba. O arquipélago de Fernando de Noronha, situado no Atlântico, também é um território pernambucano.
O estado possui extensão territorial de 98.146,315 quilômetros quadrados, sendo o relevo caracterizado por planície litorânea, planalto e depressões. Os climas predominantes são o tropical atlântico e o semiárido; a vegetação é marcada por áreas de caatinga, mangues e floresta tropical. Os principais rios que compõem a rede hidrográfica são o Capibaribe, Ipojuca, Pajeú e São Francisco.
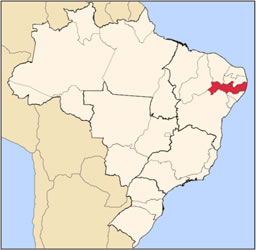
Localização de Pernambuco no mapa do Brasil
De acordo com dados divulgados em 2010, pelo Instituto Brasileiro de Geografia e Estatística (IBGE), Pernambuco, com 8.796.032 habitantes, é o segundo estado mais populoso do Nordeste, atrás somente da Bahia. Esse contingente populacional, cuja capital é recife, está distribuído em 185 municípios.
Na economia, Pernambuco tem no setor de serviços a principal fonte de receitas financeiras. As belezas naturais do estado e a excelente estrutura hoteleira atraem milhões de turistas anualmente. A agricultura baseia-se nos cultivos de cana-de-açúcar, mandioca, milho, feijão, frutas, etc. A indústria, por sua vez, está se diversificando, com destaque para os segmentos petroquímico, confecções e farmacêutico.
Apesar do constante desenvolvimento econômico, alguns problemas socioeconômicos não são solucionados. O estado detém uma das maiores taxas de mortalidade infantil do Brasil: 37,1 óbitos a cada mil nascidos vivos. O déficit nos serviços de saneamento ambiental também é preocupante.
alunosonline
Sistemas
Equações Lineares
As equações do tipo a1x1 + a2x2 + a3x3 + .....+ anxn = b, são equações lineares, onde a1, a2, a3, ... são os coeficientes; x1, x2, x3,... as incógnitas e b o termo independente.
A equação 4x – 3y + 5z = 31 é uma equação linear. Os coeficientes são 4, –3 e 5; x, y e z as incógnitas e 31 o termo independente.
Para x = 2, y = 4 e z = 7, temos 4*2 – 3*4 + 5*7 = 31, concluímos que o terno ordenado (2,4,7) é solução da equação linear
4x – 3y + 5z = 31.
Para x = 1, y = 0 e z = 3, temos 4*1 – 3*0 + 5*3 ≠ 31, concluímos que o terno ordenado (1,0,3) não é solução da equação linear
4x – 3y + 5z = 31.
Sistemas Lineares
Dizemos que o conjunto de equações lineares forma um sistema linear.
Exemplos
2x + 3y = 10
x – 5y = 2
Sistema linear com duas equações e duas incógnitas.
5x – 6y – 2z = 15
9x – 10y + 5z = 20
Sistema linear com duas equações e três incógnitas.
x + 9y + 6z = 20
3x – 10y – 12z = 5
-x + y + z = 23
Sistema linear com três equações e três incógnitas.
x+ y + z + w = 36
2x – y +2z + 9w = 40
-5x + 3y – 5z + 5w = 16
Sistema linear com três equações e quatro incógnitas.
O sistema linear abaixo admite o terno ordenado (1, 2, 3) como solução.
x + 2y – z = 2
2x – y + z = 3
x + y + z = 6
1 + 2*2 – 3 = 2 → 1+ 4 – 3 = 2 → 2 = 2
2*1 – 2 + 3 = 3 → 2 – 2 + 3 = 2 → 3 = 3
1 + 2 + 3 = 6 → 6 = 6
No entanto, ele não admite como solução o terno ordenado (1, 2, 4).
1 + 2*2 – 3 = 2 → 1+ 4 – 3 = 2 → 2 = 2
2*1 – 2 + 3 = 3 → 2 – 2 + 3 = 2 → 3 = 3
1 + 2 + 4 = 6 → 7 ≠ 6
extraido de www.mundoeducacao.com.br
As equações do tipo a1x1 + a2x2 + a3x3 + .....+ anxn = b, são equações lineares, onde a1, a2, a3, ... são os coeficientes; x1, x2, x3,... as incógnitas e b o termo independente.
A equação 4x – 3y + 5z = 31 é uma equação linear. Os coeficientes são 4, –3 e 5; x, y e z as incógnitas e 31 o termo independente.
Para x = 2, y = 4 e z = 7, temos 4*2 – 3*4 + 5*7 = 31, concluímos que o terno ordenado (2,4,7) é solução da equação linear
4x – 3y + 5z = 31.
Para x = 1, y = 0 e z = 3, temos 4*1 – 3*0 + 5*3 ≠ 31, concluímos que o terno ordenado (1,0,3) não é solução da equação linear
4x – 3y + 5z = 31.
Sistemas Lineares
Dizemos que o conjunto de equações lineares forma um sistema linear.
Exemplos
2x + 3y = 10
x – 5y = 2
Sistema linear com duas equações e duas incógnitas.
5x – 6y – 2z = 15
9x – 10y + 5z = 20
Sistema linear com duas equações e três incógnitas.
x + 9y + 6z = 20
3x – 10y – 12z = 5
-x + y + z = 23
Sistema linear com três equações e três incógnitas.
x+ y + z + w = 36
2x – y +2z + 9w = 40
-5x + 3y – 5z + 5w = 16
Sistema linear com três equações e quatro incógnitas.
O sistema linear abaixo admite o terno ordenado (1, 2, 3) como solução.
x + 2y – z = 2
2x – y + z = 3
x + y + z = 6
1 + 2*2 – 3 = 2 → 1+ 4 – 3 = 2 → 2 = 2
2*1 – 2 + 3 = 3 → 2 – 2 + 3 = 2 → 3 = 3
1 + 2 + 3 = 6 → 6 = 6
No entanto, ele não admite como solução o terno ordenado (1, 2, 4).
1 + 2*2 – 3 = 2 → 1+ 4 – 3 = 2 → 2 = 2
2*1 – 2 + 3 = 3 → 2 – 2 + 3 = 2 → 3 = 3
1 + 2 + 4 = 6 → 7 ≠ 6
extraido de www.mundoeducacao.com.br
Modulo de um número
Podemos dizer que módulo é o mesmo que distância de um número real ao número zero, pois o módulo de número real surgiu da necessidade de medir a distância de um número negativo ao zero.
Ao medirmos a distância de um número negativo qualquer ao zero percebe-se que a distância fica negativa e como não é usual dizer que uma distância ou comprimento é negativo foi criado o módulo de número real que torna o valor positivo ou nulo.
Assim, podemos dizer que o módulo de um número real irá seguir duas opções:
• O módulo ou valor absoluto de um número real é o próprio número, se ele for positivo.
• O módulo ou valor absoluto de um número real será o seu simétrico, se ele for negativo.
A representação de um módulo ou valor absoluto de um número real é feito por duas barras paralelas.
Veja o resumo da definição de módulo de um número real abaixo:
|x| = x, se x ≥ 0
-x, se x < 0
Veja alguns exemplos de como calcular módulo ou valor absoluto de números reais.
• |+4| = 4
• |-3| = - (-3) = 3
• |10 – 6 | = |+4| = 4
• |-1 – 3| = |-4| = - (-4) = 4
• |-1| + |5| - |6| = -(-1) + 5 – 6 = 1 + 5 - 6 = 6 – 6 = 0
• - | -8| = -[-(-8)] = - 8
Veja alguns exemplos de como encontrar o módulo de valores desconhecidos.
• |x + 2| nesse caso teremos duas opções, pois não sabemos o valor da incógnita x. Assim, seguimos a definição:
x + 2, se x + 2 ≥ 0, ou seja, x ≥ -2
- (x + 2), se x + 2 < 0, ou seja, x < -2
• |2x – 10|
2x – 10, se 2x – 10 ≥ 0, ou seja, 2x ≥ 10 → x ≥ 5
-(2x – 10), se 2x – 10 < 0, ou seja, 2x < 10 → x < 5
• |x2 – 9|
x 2 – 9, se x2 – 9 ≥ 0
x 2 – 9 ≥ 0
x 2 ≥ 9
x ≥ 3 ou x ≤ -3
- (x 2 – 9) , se x2 – 9 < 0
x2 – 9 < 0
x2 < 9
-3 < x < 3
Ao medirmos a distância de um número negativo qualquer ao zero percebe-se que a distância fica negativa e como não é usual dizer que uma distância ou comprimento é negativo foi criado o módulo de número real que torna o valor positivo ou nulo.
Assim, podemos dizer que o módulo de um número real irá seguir duas opções:
• O módulo ou valor absoluto de um número real é o próprio número, se ele for positivo.
• O módulo ou valor absoluto de um número real será o seu simétrico, se ele for negativo.
A representação de um módulo ou valor absoluto de um número real é feito por duas barras paralelas.
Veja o resumo da definição de módulo de um número real abaixo:
|x| = x, se x ≥ 0
-x, se x < 0
Veja alguns exemplos de como calcular módulo ou valor absoluto de números reais.
• |+4| = 4
• |-3| = - (-3) = 3
• |10 – 6 | = |+4| = 4
• |-1 – 3| = |-4| = - (-4) = 4
• |-1| + |5| - |6| = -(-1) + 5 – 6 = 1 + 5 - 6 = 6 – 6 = 0
• - | -8| = -[-(-8)] = - 8
Veja alguns exemplos de como encontrar o módulo de valores desconhecidos.
• |x + 2| nesse caso teremos duas opções, pois não sabemos o valor da incógnita x. Assim, seguimos a definição:
x + 2, se x + 2 ≥ 0, ou seja, x ≥ -2
- (x + 2), se x + 2 < 0, ou seja, x < -2
• |2x – 10|
2x – 10, se 2x – 10 ≥ 0, ou seja, 2x ≥ 10 → x ≥ 5
-(2x – 10), se 2x – 10 < 0, ou seja, 2x < 10 → x < 5
• |x2 – 9|
x 2 – 9, se x2 – 9 ≥ 0
x 2 – 9 ≥ 0
x 2 ≥ 9
x ≥ 3 ou x ≤ -3
- (x 2 – 9) , se x2 – 9 < 0
x2 – 9 < 0
x2 < 9
-3 < x < 3
Equação Fundamental da Reta
Podemos determinar a equação fundamental de uma reta utilizando o ângulo
formado pela reta com o eixo das abscissas (x) e as coordenadas de um
ponto pertencente à reta. O coeficiente angular da reta, associado à
coordenada do ponto, facilita a representação da equação da reta.
Observe:
Considerando uma reta r, o ponto C(xC, yC) pertencente à reta, seu coeficiente angular m e outro ponto D(x,y) genérico diferente de C. Com dois pontos pertencentes a reta r, um real e outro genérico, podemos calcular o seu coeficiente angular.
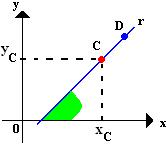
m = y – y0/x – x0
m (x – x0) = y – y0
Portanto, a equação fundamental da reta será determinada pela seguinte expressão:
y – y0 = m (x – x0)
Exemplo 1
Encontre a equação fundamental da reta r que possui o ponto A (0,-3/2) e coeficiente angular igual a m = – 2.
y – y0 = m (x – x0)
y – (–3/2) = –2(x – 0)
y + 3/2 = –2x
2x + y + 3/2 = 0
Exemplo 2
Obtenha uma equação para a reta representada abaixo:
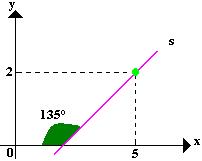
Para determinarmos a equação fundamental da reta precisamos das coordenadas de um dos pontos pertencentes à reta e o valor do coeficiente angular. As coordenadas do ponto fornecido é (5,2), o coeficiente angular é a tangente do ângulo α.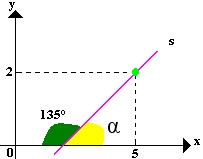
Iremos obter o valor de α com a diferença 180° – 135° = 45°, então α = 45º e a tg 45° = 1.
y – y0 = m (x – x0)
y – 2 = 1 (x – 5)
y – 2 = x – 5
y – x + 3 = 0
Exemplo 3
Determine a equação da reta que passa pelo ponto de coordenadas (6; 2) e possui inclinação de 60º.
Coeficiente angular é dado pela tangente do ângulo 60º: tg 60º = √3.
y – y0 = m (x – x0)
y – 2 = √3 (x – 6)
y – 2 = √3x – 6√3
–√3x + y – 2 + 6√3 = 0
√3x – y + 2 – 6 √3 = 0
Marcos Noé
Considerando uma reta r, o ponto C(xC, yC) pertencente à reta, seu coeficiente angular m e outro ponto D(x,y) genérico diferente de C. Com dois pontos pertencentes a reta r, um real e outro genérico, podemos calcular o seu coeficiente angular.

m = y – y0/x – x0
m (x – x0) = y – y0
Portanto, a equação fundamental da reta será determinada pela seguinte expressão:
y – y0 = m (x – x0)
Exemplo 1
Encontre a equação fundamental da reta r que possui o ponto A (0,-3/2) e coeficiente angular igual a m = – 2.
y – y0 = m (x – x0)
y – (–3/2) = –2(x – 0)
y + 3/2 = –2x
2x + y + 3/2 = 0
Exemplo 2
Obtenha uma equação para a reta representada abaixo:

Para determinarmos a equação fundamental da reta precisamos das coordenadas de um dos pontos pertencentes à reta e o valor do coeficiente angular. As coordenadas do ponto fornecido é (5,2), o coeficiente angular é a tangente do ângulo α.

Iremos obter o valor de α com a diferença 180° – 135° = 45°, então α = 45º e a tg 45° = 1.
y – y0 = m (x – x0)
y – 2 = 1 (x – 5)
y – 2 = x – 5
y – x + 3 = 0
Exemplo 3
Determine a equação da reta que passa pelo ponto de coordenadas (6; 2) e possui inclinação de 60º.
Coeficiente angular é dado pela tangente do ângulo 60º: tg 60º = √3.
y – y0 = m (x – x0)
y – 2 = √3 (x – 6)
y – 2 = √3x – 6√3
–√3x + y – 2 + 6√3 = 0
√3x – y + 2 – 6 √3 = 0
Marcos Noé
Assinar:
Postagens (Atom)

.jpg)