www.youtube.com/accbarroso1
Vinte de novembro é o Dia Nacional da Consciência Negra. A data - transformada em Dia Nacional da Consciência Negra pelo Movimento Negro Unificado em 1978 - não foi escolhida ao acaso, e sim como homenagem a Zumbi, líder máximo do Quilombo de Palmares e símbolo da resistência negra, assassinado em 20 de novembro de 1695.
O Quilombo dos Palmares foi fundado no ano de 1597, por cerca de 40 escravos foragidos de um engenho situado em terras pernambucanas. Em pouco tempo, a organização dos fundadores fez com que o quilombo se tornasse uma verdadeira cidade. Os negros que escapavam da lida e dos ferros não pensavam duas vezes: o destino era o tal quilombo cheio de palmeiras.
Com a chegada de mais e mais pessoas, inclusive índios e brancos foragidos, formaram-se os mocambos, que funcionavam como vilas. O mocambo do macaco, localizado na Serra da Barriga, era a sede administrativa do povo quilombola. Um negro chamado Ganga Zumba foi o primeiro rei do Quilombo dos Palmares.
Alguns anos após a sua fundação,o Quilombo dos Palmares foi invadido por uma expedição bandeirante. Muitos habitantes, inclusive crianças, foram degolados. Um recém-nascido foi levado pelos invasores e entregue como presente a Antônio Melo, um padre da vila de Recife.
O menino, batizado pelo padre com o nome de Francisco, foi criado e educado pelo religioso, que lhe ensinou a ler e escrever, além de lhe dar noções de latim, e o iniciar no estudo da Bíblia. Aos 12 anos o menino era coroinha. Entretanto, a população local não aprovava a atitude do pároco, que criava o negrinho como filho, e não como servo.
Apesar do carinho que sentia pelo seu pai adotivo, Francisco não se conformava em ser tratado de forma diferente por causa de sua cor. E sofria muito vendo seus irmãos de raça sendo humilhados e mortos nos engenhos e praças públicas. Por isso, quando completou 15 anos, o franzino Francisco fugiu e foi em busca do seu lugar de origem, o Quilombo dos Palmares.
Após caminhar cerca de 132 quilômetros, o garoto chegou à Serra da Barriga. Como era de costume nos quilombos, recebeu uma família e um novo nome. Agora, Francisco era Zumbi. Com os conhecimentos repassados pelo padre, Zumbi logo superou seus irmãos em inteligência e coragem. Aos 17 anos tornou-se general de armas do quilombo, uma espécie de ministro de guerra nos dias de hoje.
Com a queda do rei Ganga Zumba, morto após acreditar num pacto de paz com os senhores de engenho, Zumbi assumiu o posto de rei e levou a luta pela liberdade até o final de seus dias. Com o extermínio do Quilombo dos Palmares pela expedição comandada pelo bandeirante Domingos Jorge Velho, em 1694, Zumbi fugiu junto a outros sobreviventes do massacre para a Serra de Dois Irmãos, então terra de Pernambuco.
Contudo, em 20 de novembro de 1695 Zumbi foi traído por um de seus principais comandantes, Antônio Soares, que trocou sua liberdade pela revelação do esconderijo. Zumbi foi então torturado e capturado. Jorge Velho matou o rei Zumbi e o decapitou, levando sua cabeça até a praça do Carmo, na cidade de Recife, onde ficou exposta por anos seguidos até sua completa decomposição.
“Deus da Guerra”, “Fantasma Imortal” ou “Morto Vivo”. Seja qual for a tradução correta do nome Zumbi, o seu significado para a história do Brasil e para o movimento negro é praticamente unânime: Zumbi dos Palmares é o maior ícone da resistência negra ao escravismo e de sua luta por liberdade. Os anos foram passando, mas o sonho de Zumbi permanece e sua história é contada com orgulho pelos habitantes da região onde o negro-rei pregou a liberdade.
No período de escravidão no Brasil (séculos XVII e XVIII), os negros que conseguiam fugir se refugiavam com outros em igual situação em locais bem escondidos e fortificados no meio das matas. Estes locais eram conhecidos como quilombos. Nestas comunidades, eles viviam de acordo com sua cultura africana, plantando e produzindo em comunidade. Na época colonial, o Brasil chegou a ter centenas destas comunidades espalhadas, principalmente, pelos atuais estados da Bahia, Pernambuco, Goiás, Mato Grosso, Minas Gerais e Alagoas.
Na ocasião em que Pernambuco foi invadida pelos holandeses (1630), muitos dos senhores de engenho acabaram por abandonar suas terras. Este fato beneficiou a fuga de um grande número de escravos. Estes, após fugirem, buscaram abrigo no Quilombo dos Palmares, localizado em Alagoas.
Esse fato propiciou o crescimento do Quilombo dos Palmares. No ano de 1670, este já abrigava em torno de 50 mil escravos. Estes, também conhecidos como quilombolas, costumavam pegar alimentos às escondidas das plantações e dos engenhos existentes em regiões próximas; situação que incomodava os habitantes.
Esta situação fez com que os quilombolas fossem combatidos tanto pelos holandeses (primeiros a combatê-los) quanto pelo governo de Pernambuco, sendo que este último contou com os serviços do bandeirante Domingos Jorge Velho.
A luta contra os negros de Palmares durou por volta de cinco anos; contudo, apesar de todo o empenho e determinação dos negros chefiados por Zumbi, eles, por fim, foram derrotados.
Os quilombos representaram uma das formas de resistência e combate à escravidão. Rejeitando a cruel forma de vida, os negros buscavam a liberdade e uma vida com dignidade, resgatando a cultura e a forma de viver que deixaram na África e contribuindo para a formação da cultura afro-brasileira.
Ao falarmos em escravidão, é difícil não pensar nos portugueses, espanhóis e ingleses que superlotavam os porões de seus navios de negros africanos, colocando-os a venda de forma desumana e cruel por toda a região da América.
Sobre este tema, é difícil não nos lembrarmos dos capitães-de-mato que perseguiam os negros que haviam fugido no Brasil, dos Palmares, da Guerra de Secessão dos Estados Unidos, da dedicação e idéias defendidas pelos abolicionistas, e de muitos outros fatos ligados a este assunto.
Apesar de todas estas citações, a escravidão é bem mais antiga do que o tráfico do povo africano. Ela vem desde os primórdios de nossa história, quando os povos vencidos em batalhas eram escravizados por seus conquistadores. Podemos citar como exemplo os hebreus, que foram vendidos como escravos desde os começos da História.
Muitas civilizações usaram e dependeram do trabalho escravo para a execução de tarefas mais pesadas e rudimentares. Grécia e Roma foi uma delas, estas detinham um grande número de escravos; contudo, muitos de seus escravos eram bem tratados e tiveram a chance de comprar sua
Escravidão no Brasil
No Brasil, a escravidão teve início com a produção de açúcar na primeira metade do século XVI. Os portugueses traziam os negros africanos de suas colônias na África para utilizar como mão-de-obra escrava nos engenhos de açúcar do Nordeste. Os comerciantes de escravos portugueses vendiam os africanos como se fossem mercadorias aqui no Brasil. Os mais saudáveis chegavam a valer o dobro daqueles mais fracos ou velhos.
O transporte era feito da África para o Brasil nos porões do navios negreiros. Amontoados, em condições desumanas, muitos morriam antes de chegar ao Brasil, sendo que os corpos eram lançados ao mar.
Nas fazendas de açúcar ou nas minas de ouro (a partir do século XVIII), os escravos eram tratados da pior forma possível. Trabalhavam muito (de sol a sol), recebendo apenas trapos de roupa e uma alimentação de péssima qualidade. Passavam as noites nas senzalas (galpões escuros, úmidos e com pouca higiene) acorrentados para evitar fugas. Eram constantemente castigados fisicamente, sendo que o açoite era a punição mais comum no Brasil Colônia.
Eram proibidos de praticar sua religião de origem africana ou de realizar suas festas e rituais africanos. Tinham que seguir a religião católica, imposta pelos senhores de engenho, adotar a língua portuguesa na comunicação. Mesmo com todas as imposições e restrições, não deixaram a cultura africana se apagar. Escondidos, realizavam seus rituais, praticavam suas festas, mantiveram suas representações artísticas e até desenvolveram uma forma de luta: a capoeira.
As mulheres negras também sofreram muito com a escravidão, embora os senhores de engenho utilizassem esta mão-de-obra, principalmente, para trabalhos domésticos. Cozinheiras, arrumadeiras e até mesmo amas de leite foram comuns naqueles tempos da colônia.
No Século do Ouro (XVIII) alguns escravos conseguiam comprar sua liberdade após adquirirem a carta de alforria. Juntando alguns "trocados" durante toda a vida, conseguiam tornar-se livres. Porém, as poucas oportunidades e o preconceito da sociedades acabavam fechando as portas para estas pessoas.
O negro também reagiu à escravidão, buscando uma vida digna. Foram comuns as revoltas nas fazendas em que grupos de escravos fugiam, formando nas florestas os famosos quilombos. Estes, eram comunidades bem organizadas, onde os integrantes viviam em liberdade, através de uma organização comunitária aos modelada.
Campanha Abolicionista e a Abolição da Escravatura
A partir da metade do século XIX a escravidão no Brasil passou a ser contestada pela Inglaterra. Interessada em ampliar seu mercado consumidor no Brasil e no mundo, o Parlamento Inglês aprovou a Lei Bill Aberdeen (1845), que proibia o tráfico de escravos, dando o poder aos ingleses de abordarem e aprisionarem navios de países que faziam esta prática.
Em 1850, o Brasil cedeu às pressões inglesas e aprovou a Lei Eusébio de Queiróz que acabou com o tráfico negreiro. Em 28 de setembro de 1871 era aprovada a Lei do Ventre Livre que dava liberdade aos filhos de escravos nascidos a partir daquela data. E no ano de 1885 era promulgada a Lei dos Sexagenários que garantia liberdade aos escravos com mais de 60 anos de idade.
Somente no final do século XIX é que a escravidão foi mundialmente proibida. Aqui no Brasil, sua abolição se deu em 13 de maio de 1888 com a promulgação da Lei Áurea, feita pela Princesa Isabel.fonte:http://conscienciapura.zip.net/
Esse é o blog do Professor de Matemática Carlos Barroso. Trabalho no Colégio Estadual Dinah Gonçalves . Valéria-Salvador-Bahia .Inscreva-se Já no meu canal www.youtube.com/accbarroso1 e receba as videoaulas de Matemática.
domingo, 1 de dezembro de 2019
Cubo perfeito
Cubo perfeito 
O cubo da soma de duas parcelas [(a + b)3] é igual ao cubo da primeira parcela [a3], mais três vezes o quadrado da primeira pela segunda [3 . a2 . b], mais três vezes a primeira pelo quadro da segunda [3 . a . b2], mais o cubo da segunda parcela [b3].
O cubo da diferença entre duas parcelas [(a – b)3] é igual ao cubo da primeira [a3], menos três vezes o quadrado da primeira pela segunda [3 . a2 . b], mais três vezes a primeira pelo quadrado da segunda [3 . a . b2], menos o cubo da segunda parcela [b3].
Justificativas

Observações:Cuidado para não confundir o cubo da soma, que é (a + b) 3, com a soma de cubos, que é a3 + b3. Ou o cubo da diferença, que é (a – b) 3, com a diferença entre cubos, que é a3 – b3.
Exemplos:
X3 + 6x2 + 12x + 8 = x3 + 3 . x2 . 2 + 3 . x . 22 + 23 = (x + 2)3
a3 – 9a2 + 27a – 27 = a3 – 3 . a2 . 3 + 3 . a . 32 – 33 = (a – 3) 3

O cubo da soma de duas parcelas [(a + b)3] é igual ao cubo da primeira parcela [a3], mais três vezes o quadrado da primeira pela segunda [3 . a2 . b], mais três vezes a primeira pelo quadro da segunda [3 . a . b2], mais o cubo da segunda parcela [b3].
O cubo da diferença entre duas parcelas [(a – b)3] é igual ao cubo da primeira [a3], menos três vezes o quadrado da primeira pela segunda [3 . a2 . b], mais três vezes a primeira pelo quadrado da segunda [3 . a . b2], menos o cubo da segunda parcela [b3].
Justificativas

Observações:Cuidado para não confundir o cubo da soma, que é (a + b) 3, com a soma de cubos, que é a3 + b3. Ou o cubo da diferença, que é (a – b) 3, com a diferença entre cubos, que é a3 – b3.
Exemplos:
X3 + 6x2 + 12x + 8 = x3 + 3 . x2 . 2 + 3 . x . 22 + 23 = (x + 2)3
a3 – 9a2 + 27a – 27 = a3 – 3 . a2 . 3 + 3 . a . 32 – 33 = (a – 3) 3
As reformas de Drácon e Sólon
Colégio Estadual Dinah Gonçalves
As reformas de Drácon e Sólon
Rainer Sousa
Drácon e Sólon: adoção de importantes transformações políticas em Atenas.
Durante o período arcaico (800 – 500 a.C.), a cidade-Estado de Atenas passou por um conjunto de transformações econômicas bastante significativo. A economia essencialmente agrícola, partiu para o desenvolvimento do comércio e da agricultura. Com isso, os proprietários de terra passaram a ter sua hegemonia política questionada por esse novo grupo de indivíduos enriquecidos. Ao mesmo tempo, parcelas menos favorecidas reivindicavam o fim da escravidão por dívidas.
Com o passar do tempo, as manifestações em favor de reformas políticas que prestigiassem outros segmentos da sociedade ateniense passaram a ganhar força. Para que tais tensões não desencadeassem uma situação de conflito maior, os aristocratas determinaram a criação dos chamados legisladores. Em termos gerais, os ocupantes desse novo cargo político teriam por atribuição empreender a promulgação de leis que equilibrassem os interesses políticos existentes naquela época.
Por volta de 621 a.C., o arconte Sólon se estabeleceu como governante de Atenas. Nessa época, elaborou um conjunto de leis escritas que pudessem superar os desentendimentos e transformações existentes na tradição oral que regiam as leis. Rígido, esse legislador impôs a morte como punição para vários crimes. Em termos práticos, essa sua medida foi de grande importância para que os eupátridas deixassem de monopolizar o conhecimento das leis, que agora estava sob a tutela do governo.
Apesar de significativas, as mudanças de Sólon não tiveram impacto direto na resolução dos conflitos de interesse que tomavam a sociedade ateniense. Foi daí que o comerciante Sólon chegou ao cargo de legislador com o intuito de interferir em uma série de questões políticas, econômicas e sociais. A partir daquele momento, o poder do cargo de legislador e o emprego das leis escritas atuaram em conjunto para conduzir reformas de peso mais significativo.
No que tange à natureza das leis, Sólon anulou alguns dos excessos que marcavam as punições anteriormente normatizadas por Drácon. Além disso, reformulou os direitos dos primogênitos no repasse das heranças e empreendeu o fim da escravidão por dívidas. Ao mesmo tempo, anulou alguns tipos de hipoteca e devolveu as terras de proprietários em dívida.
Em âmbito econômico, incentivou a exploração das minas localizadas na região de Laurion, organizou um sistema de pesos e medidas e proibiu a exportação de cereais. Para dinamizar as atividades comerciais, criou um padrão monetário fixo para a cidade e permitiu a entrada de artesãos estrangeiros nesse mesmo ambiente. Por meio dessas ações, tal legislador procurou expandir as atividades comerciais e as manufaturas.
No que se refere aos organismos de participação política, Sólon formulou um novo sistema de participação política feito a partir da condição financeira de cada participante. Desse modo, ele conseguiu oferecer uma participação mais ampla dos cidadãos atenienses na esfera política. Ao longo do tempo, suas ações foram de grande peso para que a democracia fosse adotada naquela cidade-Estado.
Com o passar do tempo, as manifestações em favor de reformas políticas que prestigiassem outros segmentos da sociedade ateniense passaram a ganhar força. Para que tais tensões não desencadeassem uma situação de conflito maior, os aristocratas determinaram a criação dos chamados legisladores. Em termos gerais, os ocupantes desse novo cargo político teriam por atribuição empreender a promulgação de leis que equilibrassem os interesses políticos existentes naquela época.
Por volta de 621 a.C., o arconte Sólon se estabeleceu como governante de Atenas. Nessa época, elaborou um conjunto de leis escritas que pudessem superar os desentendimentos e transformações existentes na tradição oral que regiam as leis. Rígido, esse legislador impôs a morte como punição para vários crimes. Em termos práticos, essa sua medida foi de grande importância para que os eupátridas deixassem de monopolizar o conhecimento das leis, que agora estava sob a tutela do governo.
Apesar de significativas, as mudanças de Sólon não tiveram impacto direto na resolução dos conflitos de interesse que tomavam a sociedade ateniense. Foi daí que o comerciante Sólon chegou ao cargo de legislador com o intuito de interferir em uma série de questões políticas, econômicas e sociais. A partir daquele momento, o poder do cargo de legislador e o emprego das leis escritas atuaram em conjunto para conduzir reformas de peso mais significativo.
No que tange à natureza das leis, Sólon anulou alguns dos excessos que marcavam as punições anteriormente normatizadas por Drácon. Além disso, reformulou os direitos dos primogênitos no repasse das heranças e empreendeu o fim da escravidão por dívidas. Ao mesmo tempo, anulou alguns tipos de hipoteca e devolveu as terras de proprietários em dívida.
Em âmbito econômico, incentivou a exploração das minas localizadas na região de Laurion, organizou um sistema de pesos e medidas e proibiu a exportação de cereais. Para dinamizar as atividades comerciais, criou um padrão monetário fixo para a cidade e permitiu a entrada de artesãos estrangeiros nesse mesmo ambiente. Por meio dessas ações, tal legislador procurou expandir as atividades comerciais e as manufaturas.
No que se refere aos organismos de participação política, Sólon formulou um novo sistema de participação política feito a partir da condição financeira de cada participante. Desse modo, ele conseguiu oferecer uma participação mais ampla dos cidadãos atenienses na esfera política. Ao longo do tempo, suas ações foram de grande peso para que a democracia fosse adotada naquela cidade-Estado.
Nova política Econômica na Rússia
Colégio Estadual Dinah Gonçalves
Nova política Econômica na Rússia
Alunos Online
Cartaz soviético da NEP: "O capitalismo a serviço do comunismo".
Em 1917 o mundo testemunhava a ascensão de uma nova organização política: o socialismo. Descontentes com a má administração do Czar Nicolau II, manifestantes de esquerda deram um golpe de Estado, decretando o fim da monarquia, na Rússia. Liderados por Vladimir Lênin, os sovietes (como eram conhecidos os revolucionários russos) adotaram um regime socialista, em que a propriedade privada e o acúmulo de riquezas seriam erradicados, vigorando a distribuição igualitária de bens, controlados pelo Estado.
No início da Revolução, a Rússia experimentou um relevante crescimento econômico. Mas, ao longo do tempo, a economia se estagnou, gerando descontentamento entre os russos. Uma crise era esperada. Lênin, temendo a perda de apoio populacional e, consequentemente, o declínio comunista, adotou medidas econômicas e políticas, a fim de sanar a crise. Uma delas foi o Comunismo de Guerra, em que foi adotada uma economia totalmente centralizada pelo Estado. Outra medida foi, em 1921, a criação da “Nova Política Econômica”, conhecida pela sigla “NEP”.
Lênin acreditava que para se conseguir um desenvolvimento econômico sólido, era preciso abrir mão do radicalismo da doutrina socialista e permitir certas práticas capitalistas. Ilustrada pela frase “Um passo atrás, dois à frente”, a NEP permitiu o controle do comércio varejista por um setor privado, a formação de cooperativas, o aluguel de terras, a abolição do trabalho compulsivo nas fábricas e a coletivização das propriedades. O Estado supervisionaria todas essas práticas, como também o controle do comércio externo, do sistema bancário e das indústrias de base.
A Nova Política Econômica lograva êxitos. A economia russa voltou a crescer, fato que possibilitou o diálogo com outras nações, perdido após a crescente da ideologia socialista. Mas, em 1924, Vladimir Lênin faleceu e o governo russo foi disputado entre Trótsky e Stálin. Este último, vencedor do embate, aboliu a NEP e instaurou os “Planos Quinquenais”, como medida econômica de seu governo.
sábado, 30 de novembro de 2019
Conjunto
Números reais
O conjunto R
O conjunto de números reais é simbolizado pela letra R. Todo número inteiro ou decimal é considerado real.
Estrutura de R
Propriedades da adição
Associativa: (x + y) + z = x + (y + z)
Comutativa: x + y = y + x
Elemento neutro: x + 0 = 0 + x = x
Simétrico Aditivo ou aposto: x + (-x) = (-x) + x = 0
Propriedades de multiplicação
Associativa: (x. y) . z = x . (y. z) Comutativa: x . y = y. x
Elemento neutro: x . 1 = 1 . x = x
Simétrico multiplicativo ou inverso: x . x-1 = x-1 . x = 1
Propriedade distributiva da multiplicação em relação á adição
x . (y + z) = xy + xz
Propriedades da Relação de ordem
Reflexiva: x ≤ x
Anti-simétrica: x ≤ y e y ≤ x ⇒ x = y Transitiva: x ≤ y e y ≤ z ⇒ x ≤ z
Tricotomia ou ordem total: x < y ou x = y ou x > y
Compatibilidade com a adição: x ≤ y ⇒ x + z ≤ y + z
Compatibilidade com a multiplicação:
z > 0 logo, x ≤ y ⇒ x . z ≤ y . z
z < 0 logo, x ≤ z ⇒ x . z ≥ y . z
Valor absoluto
Considere . Sendo assim, o módulo de x (valor absoluto de x), é um número real positivo, representado por |x|. Este número é determinado desta maneira:
x ≥ 0 ⇒ |x| = x
x ≥ 0 ⇒ |x| = - x
O conjunto R
O conjunto de números reais é simbolizado pela letra R. Todo número inteiro ou decimal é considerado real.
Estrutura de R
Propriedades da adição
Associativa: (x + y) + z = x + (y + z)
Comutativa: x + y = y + x
Elemento neutro: x + 0 = 0 + x = x
Simétrico Aditivo ou aposto: x + (-x) = (-x) + x = 0
Propriedades de multiplicação
Associativa: (x. y) . z = x . (y. z) Comutativa: x . y = y. x
Elemento neutro: x . 1 = 1 . x = x
Simétrico multiplicativo ou inverso: x . x-1 = x-1 . x = 1
Propriedade distributiva da multiplicação em relação á adição
x . (y + z) = xy + xz
Propriedades da Relação de ordem
Reflexiva: x ≤ x
Anti-simétrica: x ≤ y e y ≤ x ⇒ x = y Transitiva: x ≤ y e y ≤ z ⇒ x ≤ z
Tricotomia ou ordem total: x < y ou x = y ou x > y
Compatibilidade com a adição: x ≤ y ⇒ x + z ≤ y + z
Compatibilidade com a multiplicação:
z > 0 logo, x ≤ y ⇒ x . z ≤ y . z
z < 0 logo, x ≤ z ⇒ x . z ≥ y . z
Valor absoluto
Considere . Sendo assim, o módulo de x (valor absoluto de x), é um número real positivo, representado por |x|. Este número é determinado desta maneira:
x ≥ 0 ⇒ |x| = x
x ≥ 0 ⇒ |x| = - x
Funções
Funções |
1 - Definição
Dados dois conjuntos A e B não vazios , chama-se função (ou aplicação) de A em B, representada por
f : A ® B ; y = f(x) , a qualquer relação binária que associa a cada elemento de A ,
um único elemento de B .
um único elemento de B .
Portanto, para que uma relação de A em B seja uma função , exige-se que a cada x Î A esteja associado um único y Î B , podendo entretanto existir y Î B que não esteja associado a nenhum elemento pertencente ao conjunto A.

Obs : na notação y = f(x) , entendemos que y é imagem de x pela função f, ou seja:
y está associado a x através da função f.
y está associado a x através da função f.
Exemplos:
f(x) = 4x+3 ; então f(2) = 4.2 + 3 = 11 e portanto , 11 é imagem de 2 pela função f ;
f(5) = 4.5 + 3 = 23 , portanto 23 é imagem de 5 pela função f , f(0) = 4.0 + 3 = 3, etc.
f(x) = 4x+3 ; então f(2) = 4.2 + 3 = 11 e portanto , 11 é imagem de 2 pela função f ;
f(5) = 4.5 + 3 = 23 , portanto 23 é imagem de 5 pela função f , f(0) = 4.0 + 3 = 3, etc.
Para definir uma função , necessitamos de dois conjuntos (Domínio e Contradomínio ) e de uma fórmula ou uma lei que relacione cada elemento do domínio a um e somente um elemento do contradomínio .
Quando D(f) (domínio) Ì R e CD(f)(contradomínio) Ì R , sendo R o conjunto dos números reais , dizemos que a função f é uma função real de variável real . Na prática , costumamos considerar uma função real de variável real como sendo apenas a lei y = f(x) que a define , sendo o conjunto dos valores possíveis para x , chamado de domínio e o conjunto dos valores possíveis para y , chamado de conjunto imagem da função . Assim, por exemplo, para a função definida por y = 1/x , temos que o seu domínio é D(f) = R* , ou seja o conjunto dos reais diferentes de zero (lembre-se que não existe divisão por zero) , e o seu conjunto imagem é também R* , já que se y = 1/x , então x = 1/y e portanto y também não pode ser zero.
Nota: o símbolo Ì significa “contido em”.
Nota: o símbolo Ì significa “contido em”.
Dada uma função f : A ® B definida por y = f(x),
podemos representar os pares ordenados (x,y) Î f onde x Î A e y Î B ,num sistema de coordenadas cartesianas .
O gráfico obtido será o gráfico da função f .
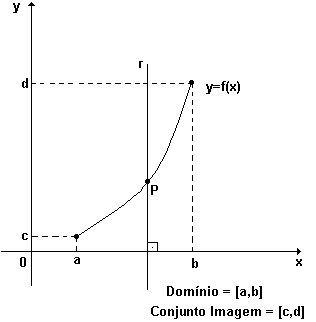
Assim , por exemplo , sendo dado o gráfico cartesiano de uma função f , podemos dizer que:
podemos representar os pares ordenados (x,y) Î f onde x Î A e y Î B ,num sistema de coordenadas cartesianas .
O gráfico obtido será o gráfico da função f .
Assim , por exemplo , sendo dado o gráfico cartesiano de uma função f , podemos dizer que:
a ) a projeção da curva sobre o eixo dos x , nos dá o domínio da função .
b ) a projeção da curva sobre o eixo dos y , nos dá o conjunto imagem da função .
c ) toda reta vertical que passa por um ponto do domínio da função , intercepta o gráfico da função em no máximo um ponto .
b ) a projeção da curva sobre o eixo dos y , nos dá o conjunto imagem da função .
c ) toda reta vertical que passa por um ponto do domínio da função , intercepta o gráfico da função em no máximo um ponto .
Veja a figura abaixo, relativa aos ítens 1, 2 e 3 acima:
2 -Tipos de funções
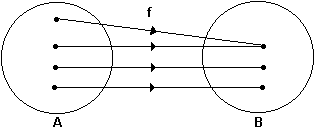
2.1 - Função sobrejetora
É aquela cujo conjunto imagem é igual ao contradomínio .
Exemplo:
Exemplo:
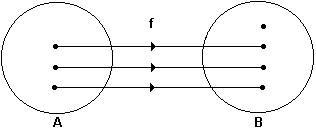
2.2 - Função injetora
Uma função y = f(x) é injetora quando elementos distintos do seu domínio , possuem imagens distintas,
isto é:
x1 ¹ x2 Þ f(x1) ¹ f(x2) .
isto é:
x1 ¹ x2 Þ f(x1) ¹ f(x2) .
Exemplo:
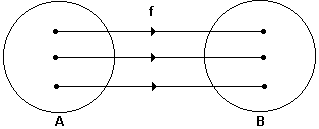
2.3 - Função bijetora
Uma função é dita bijetora , quando é ao mesmo tempo , injetora e sobrejetora .
Exemplo:
Exercícios resolvidos:
1 - Considere três funções f, g e h, tais que:
A função f atribui a cada pessoa do mundo, a sua idade.
A função g atribui a cada país, a sua capital
A função h atribui a cada número natural, o seu dobro.
A função f atribui a cada pessoa do mundo, a sua idade.
A função g atribui a cada país, a sua capital
A função h atribui a cada número natural, o seu dobro.
Podemos afirmar que, das funções dadas, são injetoras:
a) f, g e h
b) f e h
c) g e h
d) apenas h
e) nenhuma delas
a) f, g e h
b) f e h
c) g e h
d) apenas h
e) nenhuma delas
Solução:
Sabemos que numa função injetora, elementos distintos do domínio, possuem imagens distintas, ou seja:
x1 ¹ x2 Þ f(x1) ¹ f(x2) .
Sabemos que numa função injetora, elementos distintos do domínio, possuem imagens distintas, ou seja:
x1 ¹ x2 Þ f(x1) ¹ f(x2) .
Logo, podemos concluir que:
f não é injetora, pois duas pessoas distintas podem ter a mesma idade.
g é injetora, pois não existem dois países distintos com a mesma capital.
h é injetora, pois dois números naturais distintos, possuem os seus dobros também distintos.
Assim é que concluímos que a alternativa correta é a de letra C.
f não é injetora, pois duas pessoas distintas podem ter a mesma idade.
g é injetora, pois não existem dois países distintos com a mesma capital.
h é injetora, pois dois números naturais distintos, possuem os seus dobros também distintos.
Assim é que concluímos que a alternativa correta é a de letra C.
2 - Seja f uma função definida em R - conjunto dos números reais - tal que
f(x - 5) = 4x. Nestas condições, pede-se determinar f(x + 5).
f(x - 5) = 4x. Nestas condições, pede-se determinar f(x + 5).
Solução:
Vamos fazer uma mudança de variável em f(x - 5) = 4x, da seguinte forma:
x - 5 = u \ x = u + 5
Substituindo agora (x - 5) pela nova variável u e x por (u + 5), vem:
f(u) = 4(u + 5) \ f(u) = 4u + 20
Vamos fazer uma mudança de variável em f(x - 5) = 4x, da seguinte forma:
x - 5 = u \ x = u + 5
Substituindo agora (x - 5) pela nova variável u e x por (u + 5), vem:
f(u) = 4(u + 5) \ f(u) = 4u + 20
Ora, se f(u) = 4u + 20, teremos:
f(x + 5) = 4(x+5) + 20 \ f(x+5) = 4x + 40
3 – UEFS 2005-1 ) Sabendo-se que a função real f(x) = ax + b é tal que f(2x2 + 1) = - 2x2 + 2,
para todo x Î R, pode-se afirmar que b/a é igual a
a) 2
b) 3/2
c) 1/2
d) -1/3
e) -3Solução:
Ora, se f(x) = ax + b, então f(2x2 + 1) = a(2x2 + 1) + b
Como f(2x2 + 1) = - 2x2 + 2, vem, igualando:
a(2x2 + 1) + b = - 2x2 + 2
Efetuando o produto indicado no primeiro membro, fica:2ax2 + a + b = -2x2 + 2
Então, poderemos escrever: 2a = -2 \ a = -2 /2 = -1
E, também, a + b = 2 ; como a = -1, vem substituindo: (-1) + b = 2 \ b = 2 + 1 = 3
Logo, o valor procurado a/b será a/b = -1 / 3 , o que nos leva tranquilamente à alternativa D.
f(x + 5) = 4(x+5) + 20 \ f(x+5) = 4x + 40
3 – UEFS 2005-1 ) Sabendo-se que a função real f(x) = ax + b é tal que f(2x2 + 1) = - 2x2 + 2,
para todo x Î R, pode-se afirmar que b/a é igual a
a) 2
b) 3/2
c) 1/2
d) -1/3
e) -3Solução:
Ora, se f(x) = ax + b, então f(2x2 + 1) = a(2x2 + 1) + b
Como f(2x2 + 1) = - 2x2 + 2, vem, igualando:
a(2x2 + 1) + b = - 2x2 + 2
Efetuando o produto indicado no primeiro membro, fica:2ax2 + a + b = -2x2 + 2
Então, poderemos escrever: 2a = -2 \ a = -2 /2 = -1
E, também, a + b = 2 ; como a = -1, vem substituindo: (-1) + b = 2 \ b = 2 + 1 = 3
Logo, o valor procurado a/b será a/b = -1 / 3 , o que nos leva tranquilamente à alternativa D.
Agora resolva este:A função f em R é tal que f(2x) = 3x + 1. Determine 2.f(3x + 1).
Resp: 9x + 5
Resp: 9x + 5
3 - Paridade das funções
3.1 - Função par
A função y = f(x) é par, quando " x Î D(f) , f(- x ) = f(x) , ou seja, para todo elemento do seu domínio,
f( x ) = f ( - x ). Portanto , numa função par, elementos simétricos possuem a mesma imagem. Uma conseqüência desse fato é que os gráficos cartesiano das funções pares, são curvas simétricas em relação ao eixo dos y ou eixo das ordenadas.
O símbolo " , lê-se “qualquer que seja”.
f( x ) = f ( - x ). Portanto , numa função par, elementos simétricos possuem a mesma imagem. Uma conseqüência desse fato é que os gráficos cartesiano das funções pares, são curvas simétricas em relação ao eixo dos y ou eixo das ordenadas.
O símbolo " , lê-se “qualquer que seja”.
Exemplo:
y = x4 + 1 é uma função par, pois f(x) = f(-x), para todo x.
Por exemplo, f(2) = 24 + 1 = 17 e f(- 2) = (-2)4 + 1 = 17
y = x4 + 1 é uma função par, pois f(x) = f(-x), para todo x.
Por exemplo, f(2) = 24 + 1 = 17 e f(- 2) = (-2)4 + 1 = 17
O gráfico abaixo, é de uma função par.
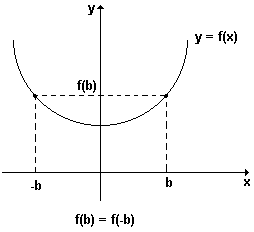
4.2 - Função ímpar
A função y = f(x) é ímpar , quando " x Î D(f) , f( - x ) = - f (x) , ou seja, para todo elemento do seu domínio, f( - x) = - f( x ). Portanto, numa função ímpar, elementos simétricos possuem imagens simétricas. Uma conseqüência desse fato é que os gráficos cartesianos das funções ímpares, são curvas simétricas em relação ao ponto (0,0), origem do sistema de eixos cartesianos.
Exemplo:
y = x3 é uma função ímpar pois para todo x, teremos f(- x) = - f(x).
Por exemplo, f( - 2) = (- 2)3 = - 8 e - f( x) = - ( 23 ) = - 8.
y = x3 é uma função ímpar pois para todo x, teremos f(- x) = - f(x).
Por exemplo, f( - 2) = (- 2)3 = - 8 e - f( x) = - ( 23 ) = - 8.
O gráfico abaixo é de uma função ímpar:
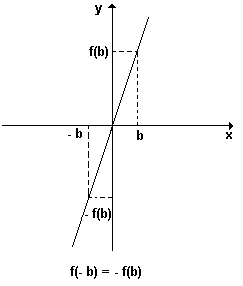
Nota: se uma função y = f(x) não é par nem ímpar, diz-se que ela não possui paridade.
Exemplo:
O gráfico abaixo, representa uma função que não possui paridade, pois a curva não é simétrica em relação ao eixo dos x e, não é simétrica em relação à origem.
Exemplo:
O gráfico abaixo, representa uma função que não possui paridade, pois a curva não é simétrica em relação ao eixo dos x e, não é simétrica em relação à origem.
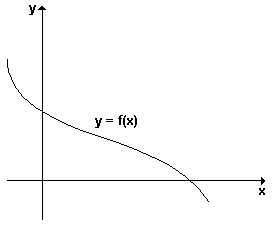
O governo de Itamar Franco
Professor de Matemática no Colégio Estadual Dinah Gonçalves
E Biologia na rede privada de Salvador-Bahia www.youtube.com/accbarroso1
Professor Antonio Carlos carneiro Barroso
email accbarroso@hotmail.com
Extraído de http://www.alunosonline.com.br
O governo de Itamar Franco

Itamar Franco, "pai" do Plano Real, que estabilizou a economia brasileira.
A principal medida adotada no governo Itamar foi a criação de um plano para barrar o crescimento da inflação: o Plano Real. Idealizado e organizado pelo Ministro da Fazenda (e posteriormente, Presidente da República) Fernando Henrique Cardoso, o Plano Real obteve êxito, reduzindo a inflação de 50% para 4%, em um mês. No dia 21 de abril de 1993, o Presidente Itamar Franco convocou um plebiscito para escolher a nova forma de governo: se manteria o presidencialismo e a república, ou se retornaria à monarquia e ao parlamentarismo. O regime republicano e presidencialista foi escolhido por uma maioria esmagadora dos votos.
Um fato curioso, acontecido no governo Itamar, foi sua sugestão à fábrica alemã Volkswagen, a retomar a fabricação do Fusca, carro muito popular nas décadas de 60 e 70, no Brasil. Itamar visava aquecer a venda de automóveis, tornando-os mais acessíveis aos brasileiros. A fábrica havia parado de fabricar o Fusca em 1978 e, a pedido do presidente, retomou sua fabricação (que cessou em 1996). O carro, apelidado de Fusca do Itamar, não atendeu às necessidades do povo, mas a ideia de popularização dos veículos foi adotada por outras fábricas.
O governo de Itamar foi curto (cerca de dois anos), mas foi o suficiente para levantar a economia nacional e, consequentemente, o orgulho dos brasileiros, ferido nos anos de chumbo da ditadura e destroçado no governo corrupto de Collor. Itamar alcançou índices tão altos de popularidade e aprovação, que seu apoio foi imprescindível para a eleição de seu Ministro e sucessor, Fernando Henrique Cardoso, nas eleições presidenciais de 1994.
sexta-feira, 29 de novembro de 2019
Assinar:
Comentários (Atom)