Regra de Sarrus
Marcos Noé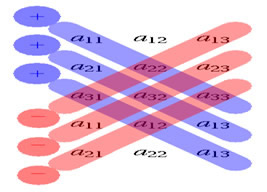
Regra de Sarrus
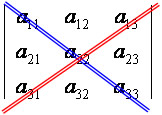
Diagonal principal: a11, a22 e a33.
Diagonal secundária: a13, a22, a31.
A aplicação da Regra de Sarrus consiste em escrever a matriz seguida da repetição de suas duas primeiras colunas. Feito esse processo, verifique a presença de três diagonais principais e três diagonais secundárias.
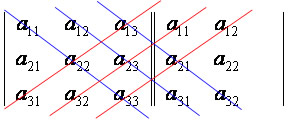
O determinante será calculado por meio da diferença entre o somatório do produto das três diagonais principais e o somatório do produto das três diagonais secundárias. Observe:
Diagonal principal
(a11 * a22 * a33) + (a12 * a23 * a31) + (a13 * a21 * a32)
Diagonal secundária
(a13 * a22 * a31) + (a11 * a23 * a32) + (a12 * a21 * a33)
Determinante
D = {(a11 * a22 * a33) + (a12 * a23 * a31) + (a13 * a21 * a32)} – {(a13 * a22 * a31) + (a11 * a23 * a32) + (a12 * a21 * a33)}
Exemplo 1:
Vamos calcular o valor do determinante da matriz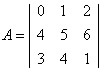 .
.
Diagonal principal
(a11 * a22 * a33) + (a12 * a23 * a31) + (a13 * a21 * a32)
Diagonal secundária
(a13 * a22 * a31) + (a11 * a23 * a32) + (a12 * a21 * a33)
Determinante
D = {(a11 * a22 * a33) + (a12 * a23 * a31) + (a13 * a21 * a32)} – {(a13 * a22 * a31) + (a11 * a23 * a32) + (a12 * a21 * a33)}
Exemplo 1:
Vamos calcular o valor do determinante da matriz
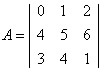 .
.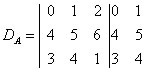
Diagonais principais
0 * 5 * 1 = 0
1 * 6 * 3 = 18
2 * 4 * 4 = 32
0 + 18 + 32 = 50
Diagonais secundárias
2 * 5 * 3 = 30
0 * 6 * 4 = 0
1 * 4 * 1 = 4
30 + 0 + 4 = 34
Determinante
DA = 50 – 34
DA = 16
Exemplo 2:
Dada a matriz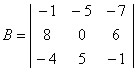 , calcule o seu determinante.
, calcule o seu determinante.
Diagonais principais
(–1) * 0 * (–1) = 0
(–5) * 6 * (–4) = 120
(–7) * (8) * (5) = – 280
0 + 120 + (–280)
120 – 280
– 160
Diagonais secundárias
(–7) * 0 * (–4) = 0
(–1) * 6 * 5 = – 30
(–5) * 8 * (–1) = 40
0 + (–30) + 40
–30 +40
10
Determinante
DB = –160 – 10
DB = – 170
0 * 5 * 1 = 0
1 * 6 * 3 = 18
2 * 4 * 4 = 32
0 + 18 + 32 = 50
Diagonais secundárias
2 * 5 * 3 = 30
0 * 6 * 4 = 0
1 * 4 * 1 = 4
30 + 0 + 4 = 34
Determinante
DA = 50 – 34
DA = 16
Exemplo 2:
Dada a matriz
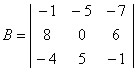 , calcule o seu determinante.
, calcule o seu determinante.Diagonais principais
(–1) * 0 * (–1) = 0
(–5) * 6 * (–4) = 120
(–7) * (8) * (5) = – 280
0 + 120 + (–280)
120 – 280
– 160
Diagonais secundárias
(–7) * 0 * (–4) = 0
(–1) * 6 * 5 = – 30
(–5) * 8 * (–1) = 40
0 + (–30) + 40
–30 +40
10
Determinante
DB = –160 – 10
DB = – 170

















