As fatorações são utilizadas no intuito de transformar expressões e equações algébricas em procedimentos envolvendo o produto de duas ou mais expressões. Dessa forma, em algumas situações, as equações podem ser resolvidas de forma simples e direta. Para a realização da fatoração simultânea, o conhecimento das técnicas envolvendo termo comum em evidência, agrupamento, diferença entre dois quadrados, trinômio quadrado perfeito e trinômio soma e produto, é de extrema importância. Em alguns polinômios, a fatoração por completo exige a utilização de duas ou mais técnicas informadas.
Observe alguns exemplos envolvendo a utilização da fatoração simultânea:
Exemplo 1
x³ + 2x² + x
1ª fatoração: fator comum em evidência
x * (x² + 2x + 1)
2ª fatoração: trinômio quadrado perfeito
x * (x + 1)²
x³ + 2x² + x → x * (x + 1)²
Exemplo 2
a²x – b²x
1ª fatoração: fator comum em evidência
x * (a² – b²)
2ª fatoração: diferença entre dois quadrados
x * (a + b) * (a – b)
a²x – b²x → x * (a + b) * (a – b)
Exemplo 3
x²b + 5bx + 6b
1ª fatoração: fator comum em evidência
b * (x² + 5x + 6)
2ª fatoração: trinômio soma e produto
b * (x + 2) * (x + 3)
x²b + 5bx + 6b → b * (x + 2) * (x + 3)
Exemplo 4
4x³ + 3x² – 4y²x – 3y²
1ª fatoração: agrupamento
x² * (4x + 3) – y² * (4x + 3)
(x² – y²) * (4x + 3)
2ª fatoração: diferença entre dois quadrados
(x + y) * (x – y) * (4x + 3)
4x³ + 3x² – 4y²x – 3y² → (x + y) * (x – y) * (4x + 3)
Exemplo 5
a³ – a
1ª fatoração: fator em evidência
a * (a² – a)
2ª fatoração: diferença entre dois quadrados
a * (a + 1 ) * (a – 1)
a³ – a → a * (a + 1 ) * (a – 1)
Exemplo 6
12x³ – 3xy²
1ª fatoração: fator em evidência
3x * (4x² – y²)
2ª fatoração: agrupamento
3x * (2x – y) * (2x + y)
12x³ – 3xy² → 3x * (2x – y) * (2x + y)
Fatorar é o mesmo que decompor o número em fatores primos, isto é, escrever um número através da multiplicação de números primos. Na fatoração utilizamos os números primos obedecendo a uma ordem crescente de acordo com as regras de divisibilidade em razão do termo a ser fatorado. Números primos são aqueles que podem ser divididos somente por um e por ele mesmo. Observe a decomposição em fatores primos dos números a seguir:
24 = 2 x 2 x 2 x 3
10 = 2 x 5
52 = 2 x 2 x 13
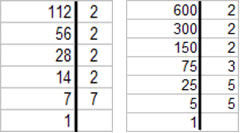
112 = 2 x 2 x 2 x 2 x 7
600 = 2 x 2 x 2 x 3 x 5 x 5
Forma prática de fatoração
O número a ser fatorado deverá ocupar a coluna da esquerda e a coluna da direita será preenchida com os fatores primos. Ao dividir o número pelo algarismo primo os resultados deverão ser colocados na coluna da direita. As divisões deverão ser efetuadas no intuito de simplificar ao máximo o número, isto é reduzi-lo ao número 1.
.jpg)
Objetivos da fatoração
Cálculo da raiz quadrada de um número.
Vamos determinar a raiz quadrada do número 144.
De acordo com a fatoração do número 144 temos: 2 x 2 x 2 x 2 x 3 x 3.
No caso da raiz quadrada, podemos representar o número 144 da seguinte forma:
2² x 2² x 3². Como o índice da raiz quadrada é 2, podemos simplificar os expoentes de valor 2 com o índice 2 da raiz. As bases dos expoentes simplificados saem da raiz multiplicadas entre si. Acompanhe a demonstração a seguir:
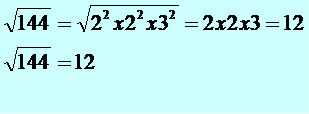.jpg)
Dado dois números quaisquer x e y. Se subtrairmos ficará: x – y, se montarmos uma expressão algébrica com os dois números obteremos: x2 + xy + y2, assim, devemos multiplicar as duas expressões encontradas.
(x - y) (x2 + xy + y2) é necessário utilizar a propriedade distributiva;
x3 + x2y + xy2 - x2y –xy2 - y3 unir os termos semelhantes;
x3 - y3 é uma expressão algébrica de dois termos, os dois estão elevados ao cubo e subtraídos.
Assim, podemos concluir que x3 - y3 é uma forma geral da soma de dois cubos onde
x e y podem assumir qualquer valor real.
A forma fatorada de x3 - y3 será (x - y) (x2 + xy + y2).
Com o conhecimento de todos os casos de fatoração, quando for preciso fatorar alguma expressão algébrica devemos sempre observar em qual dos casos ela se enquadra, veja os exemplos de como fazer esse reconhecimento.
Exemplo:
Se tivermos que fatorar a seguinte expressão algébrica 27x3 – y3 devemos observar que ela tem dois termos. Lembrando dos casos de fatoração, o único caso que fatora dois termos é a diferença de dois quadrados, soma de dois cubos e a diferença de dois cubos.
No exemplo acima os dois termos estão ao cubo e entre eles há uma subtração, então devemos utilizar o 7º caso de fatoração (diferença de dois cubos), para fatorarmos devemos escrever a expressão algébrica 27x3 – y3 da seguinte forma:
(x - y) (x2 + xy + y2). Ao tirar as raízes cúbicas dos dois termos, temos: 27x3 – y3.
A raiz cúbica de 27x3 é 3x e a raiz cúbica de y3 é y. Agora, basta substituir valores, no lugar de x colocaremos 2x e no lugar de y colocaremos 3 na forma fatorada
(x - y) (x2 + xy + y2) , ficando assim:
(3x – y) ((3x)2 + 3x . y + y2)
(3x – y) (9x2 + 3xy + y2)
Então, (2x – 3) (4x2 + 6x + 9) é a forma fatorada da expressão algébrica 8x3 – 27.
Exemplo 2
Para resolvemos a fatoração utilizando a diferença de dois cubos devemos seguir os mesmos passos do exemplo anterior. Fatorando a expressão algébrica r3 – 64 temos: As raízes cúbicas de r3 é r e de 64 é 4, substituindo teremos no lugar de x o r e no lugar de y o 4.
(r – 4) (r2 + 4r + 16) é a forma fatorada de r3 – 64.
Dado dois números quaisquer x e y, se somarmos os dois obteremos x + y, se montarmos uma expressão algébrica com os dois números teremos x2 - xy + y2, agora devemos multiplicar as duas expressões encontradas.
(x + y) (x2 - xy + y2) utilize a propriedade distributiva;
x3 - x2y + xy2 + x2y –xy2 + y3 una os termos semelhantes;
x3 + y3 é uma expressão algébrica de dois termos onde os dois estão elevados ao cubo e somados.
Assim, podemos concluir que x3 + y3 é uma forma geral da soma de dois cubos onde
x e y poderão assumir qualquer valor real.
A forma fatorada de x3 + y3 será (x + y) (x2 - xy + y2).
Veja alguns exemplos:
Exemplo1:
27x3 + 1000 é a soma de dois cubos.
Podemos escrever essa expressão da seguinte forma:
33x3 + 103, assim: x = 3x e y = 10
Agora, basta usarmos a forma geral e fazermos as substituições.
(x + y) (x2 - xy + y2)
(3x + 10) ((3x)2 – 3x . 10 + 102)
(3x + 10) (9x2 – 30x + 100)
Portanto, a fatoração de 27x3 + 1000 será (3x + 10) (9x2 – 30x + 100).
Exemplo 2:
x3 + 1 é a soma de dois cubos.
Podemos escrever essa expressão da seguinte forma:
(x)3 + 13 assim: x = x e y = 1
Agora, basta usarmos a forma gral e fazermos as substituições.
(x + y) (x2 - xy + y2)
(x + 1) ((x)2 –x .1 + 12)
(x – 1) (x2 –x + 1)
Exemplo 3:
8x3 + y3 é a soma de dois cubos.
Podemos escrever essa expressão da seguinte forma:
(2x)3 + y3 assim: x = 2x e y = y
Agora, basta usarmos a forma gral e fazermos as substituições.
(x + y) (x2 - xy + y2)
(2x + y) ((2x)2 – 2xy + y2)
(2x + y) (4x2 – 2xy + y2)
Para fatorar uma expressão algébrica utilizando esse primeiro caso de fatoração, todos os monômios da expressão algébrica devem ter pelo menos algum termo em comum.
A fatoração é feita colocando o termo comum em evidência, veja alguns exemplos:
►a – ab é uma expressão algébrica, veja como devemos fatorar:
É preciso analisar se o 1º caso poderá ser utilizado para a fatoração, então é necessário analisar todos os seus monômios (termos) para ver se há termos em comum.
a – ab essa expressão tem dois monômios a e ab
Os dois possuem termos semelhantes: o termo semelhante é a. Então, colocamos esse termo comum em evidência.
Quando colocamos a em evidência devemos dividir a e ab (os monômios) por a (termo comum), assim:
a : a = 1, pois todo número (ou letra) dividido por ele mesmo é igual a 1.
ab : a = b, pois a : a = 1, então ficaria 1b que é o mesmo que b.
Portanto a – ab = a (1 – b)
↓
Termos
em evidência
►a3 – 4a2 é uma expressão algébrica, veja como fatorar:
Essa expressão algébrica tem 2 monômios a3 e 4a2, eles têm o a como termo semelhante, então podemos colocá-lo em evidência, mas poderá surgir uma dúvida, devemos colocar o a3 ou a2? Devemos colocar sempre o de menor expoente, então colocamos a2.
Assim, devemos dividir a3 e 4a2 por a2, assim:
a3 : a2 = a, pois a3 = a .a .a, então a . a . a : a2 é o mesmo que 1a = a.
4a2 : a2 = 4, pois a2 : a2 = 1, então ficaria 4 . 1 que é mesmo que 4.
Portanto a3 – 4a2 = a2 (a – 4).
↓
Termos
em evidência
►x4 - 2x3 + x2 + x é uma expressão algébrica que tem quatro monômios, eles têm termos em comum, como esses termos têm mesma base devemos pegar o de menor expoente, então o termo em comum é x.
O termo em evidência deverá ser dividido pelos monômios x4 , 2x2 , x2 e x, assim:
x4 : x = x3, pois em bases iguais conservamos a base e diminuímos os expoentes.
2x3 : x = 2x2, pois em bases iguais conservamos a base e diminuímos os expoentes.
x2 : x = x, pois em bases iguais conservamos a base e diminuímos os expoentes.
x : x = 1, pois qualquer número ou letra dividido por ele mesmo é igual a 1.
Portanto x4 - 2x3 + x2 + x = x (x3 – 2x2 + x – 1).
↓
Termos
em evidência
► 4r + 12 é uma expressão algébrica, olhando rapidamente podemos pensar que não existe termo semelhante, o que seria errado, pois o número 12 pode ser fatorado em dois fatores 12 = 4 . 3, com essa fatoração percebemos que há um termo em comum na expressão algébrica, esse é o 4.
Então, pegamos os monômios 4r e 12 e dividimos por 4, ficando assim:
4r : 4 = 1r ou r
12 : 4 = 3
Portanto, 4r + 12 = 4 (r + 3)
↓
Termos
em evidência
► Para fatorarmos a expressão algébrica (x + 1) (x – 3) + 2 (x + 1) devemos ter um pouco mais de cuidado, pois em primeiro lugar separamos os termos:
(x + 1) (x – 3) + 2 (x + 1) a expressão possui dois termos.
↓ ↓
1º termo 2º termo
O termo semelhante é (x + 1), pois é encontrado tanto no 1º termo, como no 2º.
Então, devemos dividir o 1º termo e o 2º por (x + 1), ficando assim:
[(x + 1) (x – 3)] : (x + 1) = (x – 3)
2 (x + 1) : (x + 1) = 2
Portanto, (x + 1) (x – 3) + 2 (x + 1) = (x + 1) (x – 3 + 2)
(x + 1) (x – 3) + 2 (x + 1) = (x + 1) (x – 1)
↓
Termos
em evidência
Para conferir se as fatorações estão corretas, basta efetuar as fatorações, veja:
Para verificar se a fatoração 4r + 12 = 4 (r + 3) está correta, basta pegar a expressão algébrica fatorada 4 (r + 3) e resolvê-la:
Aplicando a propriedade distributiva temos: 4 (r + 3) = 4 . r + 4 . 3 = 4r + 12. Podemos concluir que a fatoração está correta.
Quando aplicamos o caso de fatoração por agrupamento, utilizamos a fatoração por termos comuns. Veja:
Se observarmos a expressão ab + 3b + 7a + 21 veremos que não são todos os monômios que têm termos semelhantes, mas podemos unir os que possuem termos semelhantes.
Assim, temos: ab + 3b + 7a + 21, agora aplicamos o 1º caso de fatoração (termo comum), colocando em evidência cada elemento comum de cada agrupamento.
ab + 3b + 7a + 21
↓ ↓
b termo 7 é o termo comum
comum
Então: b (a + 3) + 7 (a + 3)
Mesmo fazendo essa fatoração observamos que ainda podemos fazer mais uma fatoração, pois os dois termos b (a + 3) e 7 (a + 3) possuem um termo em comum
(a + 3). Então, aplicamos o processo do fator comum, ficando assim a fatoração:
b (a + 3) + 7 (a + 3)
(a + 3) (b + 7)
Portanto, a expressão algébrica ab + 3b + 7a + 21 fatorada fica assim: (a + 3) (b + 7).
Dada a expressão algébrica y2 – 5y + 6, sabemos que é um trinômio, mas os seus dois membros das extremidades não estão elevados ao quadrado, assim descarta a possibilidade de ser quadrado perfeito.
Então, o único caso de fatoração que podemos utilizar para fatorar essa expressão algébrica é x2 + Sx + P. Dada a expressão y2 – 5y + 6, observe se ela está em ordem decrescente de seus expoentes (do maior para o menor), se estiver basta achar dois números que somados resultem em -5 e que o produto deles resulte em 6.
Vamos fazer as tentativas para que o produto resulte em 6:
2 . 3 = 6
(- 2) . (- 3) = 6
6 . 1= 6
- 6 . (- 1) = 6
Devemos, dentre essas possibilidades, achar uma que a soma dos números dê -5. Concluímos que -2 + (-3) = -5, portanto a forma fatorada desse trinômio será:
(y – 2) (y – 3).
Dada a expressão m2 + 7m – 8, devemos achar dois números que somados resulte 7 e o produto deles seja -8. Verificamos as possibilidades do produto resultar em - 8:
- 1 . 8 = - 8
1 . (-8) = - 8
4 . (- 2) = - 8
- 4 . 2 = - 8
Devemos, dentre essas possibilidades, achar uma que a soma dos números dê 7. Concluímos que -1 + 8 = 7, portanto a forma fatorada desse trinômio será:
(m – 1) (m + 8).
Dado a expressão x2 + 4x – 12, devemos achar dois números que somados resulte em 4 e o produto do mesmo seja – 12. Verifiquemos as possibilidades de o produto resultar em -12:
1 .(-12) = -12
-1 . 12 = -12
6 . (-2) = -12
- 6 . 2 = -12
Devemos, dentre essas possibilidades, achar uma que a soma dos números dê 4. Concluímos que 6 +(- 2) = 4, portanto a forma fatorada desse trinômio será:
(x + 6) (x – 2)
Esse caso de fatoração só pode ser utilizado em expressões algébricas que possuem dois monômios e os mesmos devem estar elevados ao quadrado (elevados à quinta potência).
Chegamos à conclusão que a diferença de dois quadrados pode ser utilizada, quando:
-Tivermos uma expressão algébrica com dois monômios (sejam binômios).
- Os dois monômios forem quadrados.
- A operação entre eles for de subtração.
Veja alguns exemplos de expressões algébricas que seguem esse modelo:
• a2 - 16
• 1 – a2
3
• 4x2 – b2
Como fazer essa fatoração
Dada a expressão algébrica 9x2 – 81, veja os passos que devemos tomar para chegarmos à forma fatorada utilizando o 5º caso de fatoração.
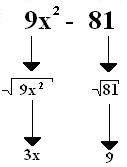
A forma fatorada será (3x – 9) (3x + 9).
Veja alguns exemplos:
Exemplo 1:
A expressão algébrica x2 – 4 é uma expressão com dois monômios e as raízes quadradas são respectivamente x e 2, então a sua forma fatorada é (x – 2) (x + 2).
Exemplo 2:
Dada a expressão algébrica 16x2 – 25, a raiz dos termos 16x2 e 25 é respectivamente 4x e 5. Então, a forma fatorada é (4x – 5) (4x + 5).
Exemplo 3:
Dada a expressão algébrica 36x2 – 81y2, a raiz dos termos 36x2 e 81y2 é respectivamente 6x e 9y. Então, a forma fatorada é (6x – 9y) (6x + 9y).
Fonte mundoeducacao.com.br









 .
.


 .
. .
.


 .
.





.jpg)
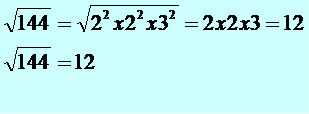.jpg)