Esse é o blog do Professor de Matemática Carlos Barroso. Trabalho no Colégio Estadual Dinah Gonçalves . Valéria-Salvador-Bahia .Inscreva-se Já no meu canal www.youtube.com/accbarroso1 e receba as videoaulas de Matemática.
quarta-feira, 4 de dezembro de 2019
Equação geral dos gases
Professor de Matemática no Colégio Estadual Dinah Gonçalves
E Biologia na rede privada de Salvador-Bahia
Professor Antonio Carlos carneiro Barroso
email accbarroso@hotmail.com
Blog HTTP://ensinodematemtica.blogspot.com e HTTP://accbarroso60.wordpress.com
http://accbarrosogestar.blogspot.com.br
http://accbarrosogestar.blogspot.com.br
Extraído de http://www.alunosonline.com.br
Equação geral dos gases
Domiciano Correa Marques da Silva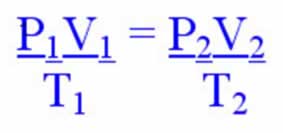
Equação geral dos gases
Nos experimentos realizados por Robert Boyle, pôde-se verificar que havia uma relação de proporção entre volume e pressão de um gás, quando a temperatura era mantida constante. Essa transformação recebeu o nome de transformação isotérmica.
Uma transformação é dita isotérmica quando a temperatura permanece constante. Nesse caso, a pressão varia de forma inversamente proporcional ao volume ocupado pelo gás.
A expressão que representa uma transformação isotérmica é conhecida como lei de Boyle-Mariotte e é representada pela seguinte equação:
p1V1 = p2V2
Onde: p1 é a pressão inicial, p2 é a pressão final, V1 volume inicial e V2 volume final.
Já o cientista Jaques Charles verificou a relação de proporção entre o volume e a temperatura de um gás quando a pressão era mantida constante.
Uma transformação é dita isobárica quando a pressão permanece constante. Nesse caso, o volume varia de forma diretamente proporcional à temperatura. A expressão para representar a transformação isobárica ficou conhecida como lei de Charles, e é representada pela equação:
V1 = V2
T1 T2
Onde: V1 volume inicial, V2 volume final, T1 temperatura inicial e T2 temperatura final.
O cientista Charles investigou também a relação existente entre a pressão e a temperatura quando o volume era mantido constante. Essa transformação é denominada isométrica, isocórica ou isovolumétrica.
Então, uma transformação é dita isovolumétrica quando o volume permanece constante, e a pressão varia proporcionalmente à temperatura. A equação que representa a lei de Charles para transformação isovolumétrica é:
p1 = p2
T1 T2
Onde: p1 é a pressão inicial, p2 é a pressão final, T1 temperatura inicial e T2 temperatura final.
Para uma transformação em que variam a pressão, o volume e a temperatura, ao mesmo tempo, temos a seguinte equação:
p1.V1 = p2.V2
T1 T2
Teorema de D’Alembert
Colégio Estadual Dinah Gonçalves
email
accbarroso@hotmail.com
matemática, os teoremas, as fórmulas, os postulados sempre recebem o nome de seus inventores e D’Alembert foi um desses, matemático e físico, foi um dos oficiais na revolução Francesa responsável pelas publicações solenes, anunciava a guerra e plocamava a paz.
Além disso, vários teoremas, tanto na física como na matemática, levaram o seu nome, na matemática podemos destacar no estudo dos polinômios o Teorema de D’Alembert, que diz:
Todo polinômio P(x) quando dividido por um binômio do tipo x – a, resultará em uma divisão exata, ou seja, terá resto igual a zero se, e somente se, a constante a for raiz do polinômio P(x).
Exemplo: Sem efetuar as divisões, prove que o polinômio P(x) = x4 - 4x3 + 4x2 - 4x +3 é divisível por x - 3 e x - i.
As divisões dadas favorecem a aplicação do Teorema de D’Alembert, dessa forma podemos afirmar que: a constante a será raiz do polinômio P(x) se, somente se, o resto da divisão for igual a zero. Dessa forma, basta aplicarmos o Teorema do Resto.
Para divisor igual a x – 3, a = 3.
P(3) = 34 – 4 . 33 + 4 . 32 – 4 . 3 + 3
P(3) = 81 – 4 . 27 + 4 . 9 – 12 + 3
P(3) = 81 – 108 + 36 – 12 + 3
P(3) = -27 + 36 – 12 + 3
P(3) = 9 – 12 + 3
P(3) = -3 + 3
P(3) = 0
Portanto, o polinômio P(x) = x4 - 4x3 + 4x2 - 4x +3 é divisível por x – 3.
Para divisor igual a x – i, a = i.
P(i) = i4 – 4 . i3 + 4 . i2 – 4 . i + 3
P(i) = 1 – 4 . (-i) + 4 . (-1) – 4i + 3
P(i) = 1 + 4i – 4 – 4i + 3
P(i) = 1 – 4 + 3
P(i) = - 3 + 3
P(i) = 0
Portanto, o polinômio P(x) = x4 - 4x3 + 4x2 - 4x +3 é divisível por x – i.
www.mundoeducacao.com.br
Conjuntos Numéricos
Os números são indispensáveis no estudo da Matemática e, por isso, são organizados em conjuntos que possuem características próprias. Ao longo da evolução da Matemática, os números foram surgindo e sendo classificados como Naturais, Inteiros, Racionais, Irracionais e Reais. Vamos conhecer cada conjunto e suas propriedades a fim de obtermos sucesso em estudos futuros.
Conjunto dos Números Naturais
Os números Naturais são representados pela letra maiúscula N e engloba todos os números inteiros positivos e o zero. Observe:
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25,...}
O conjunto dos números Naturais é considerado infinito, isto é, não possui fim. Uma característica dos números Naturais é a utilização na contagem de objetos.
Conjunto dos Números Inteiros
Os números Inteiros são representados pela letra maiúscula Z e aborda todos os números inteiros positivos, negativos e o zero. Veja:
Z = {..., -10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,...}
O conjunto dos números Inteiros é considerado infinito. Como característica dos algarismos Inteiros, temos as representações de números negativos, como medidas de temperatura, saldos negativos, situações abaixo do nível do mar entre outras.
Conjunto dos Números Racionais
Os números racionais são representados pela letra maiúscula Q e agrupa todos os números inteiros positivos, negativos, o zero, números na forma decimal e os números fracionários, aqueles na forma de a/b com b ≠ 0.

Todos os números em que a divisão é uma dízima periódica são considerados números racionais. Exemplos:

As dízimas periódicas são números resultados de uma divisão, onde à direita da vírgula temos a formação de períodos. Observe:
A dízima 0,666... possui como período o número 6.
A dízima 0,727272... possui como período o número 72.
Toda dízima periódica possui uma representação na forma de fração. Veja:

Os números Racionais são utilizados para representar partes de um inteiro. Esse conjunto também é considerado infinito.
Conjunto dos Números Irracionais
Os números Irracionais são representados pela letra maiúscula I, o grupo é formado pelos números que não possuem representação fracionária. Os números são considerados dízimas não periódicas, isto é, são infinitos, mas a sua composição não fornece períodos.
√2 = 1,4142135623730950488016887242097...
√3 = 1,7320508075688772935274463415059...
–√7 = 2,6457513110645905905016157536393...
–√11 = 3,3166247903553998491149327366707...
Conjunto dos Números Reais
O conjunto dos números Reais é formado pela união dos conjuntos dos números Naturais, Inteiros, Racionais e Irracionais.

Conjunto dos Números Primos
Esse conjunto reúne todos os números Naturais que são divisíveis somente por 1 e por ele mesmo. Observe o Crivo de Eratóstenes a seguir, ele apresentará em azul os números primos de 1 a 100.

O número 2 é o único número primo par. Possui como divisores os números 1 e 2. Observe que todos os números primos indicados obedecem a essa característica.
www.bancodeconcursos.com
Conjunto dos Números Naturais
Os números Naturais são representados pela letra maiúscula N e engloba todos os números inteiros positivos e o zero. Observe:
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25,...}
O conjunto dos números Naturais é considerado infinito, isto é, não possui fim. Uma característica dos números Naturais é a utilização na contagem de objetos.
Conjunto dos Números Inteiros
Os números Inteiros são representados pela letra maiúscula Z e aborda todos os números inteiros positivos, negativos e o zero. Veja:
Z = {..., -10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,...}
O conjunto dos números Inteiros é considerado infinito. Como característica dos algarismos Inteiros, temos as representações de números negativos, como medidas de temperatura, saldos negativos, situações abaixo do nível do mar entre outras.
Conjunto dos Números Racionais
Os números racionais são representados pela letra maiúscula Q e agrupa todos os números inteiros positivos, negativos, o zero, números na forma decimal e os números fracionários, aqueles na forma de a/b com b ≠ 0.

Todos os números em que a divisão é uma dízima periódica são considerados números racionais. Exemplos:

As dízimas periódicas são números resultados de uma divisão, onde à direita da vírgula temos a formação de períodos. Observe:
A dízima 0,666... possui como período o número 6.
A dízima 0,727272... possui como período o número 72.
Toda dízima periódica possui uma representação na forma de fração. Veja:

Os números Racionais são utilizados para representar partes de um inteiro. Esse conjunto também é considerado infinito.
Conjunto dos Números Irracionais
Os números Irracionais são representados pela letra maiúscula I, o grupo é formado pelos números que não possuem representação fracionária. Os números são considerados dízimas não periódicas, isto é, são infinitos, mas a sua composição não fornece períodos.
√2 = 1,4142135623730950488016887242097...
√3 = 1,7320508075688772935274463415059...
–√7 = 2,6457513110645905905016157536393...
–√11 = 3,3166247903553998491149327366707...
Conjunto dos Números Reais
O conjunto dos números Reais é formado pela união dos conjuntos dos números Naturais, Inteiros, Racionais e Irracionais.

Conjunto dos Números Primos
Esse conjunto reúne todos os números Naturais que são divisíveis somente por 1 e por ele mesmo. Observe o Crivo de Eratóstenes a seguir, ele apresentará em azul os números primos de 1 a 100.

O número 2 é o único número primo par. Possui como divisores os números 1 e 2. Observe que todos os números primos indicados obedecem a essa característica.
www.bancodeconcursos.com
Gráfico de Inequações do 1º Grau
Diferente das equações, as inequações são expressões matemáticas que apresentam em sua configuração sinais de desigualdade. Veja:
>: maior que
<: menor que
≥: maior ou igual que
≤: menor ou igual que
As inequações são utilizadas em cálculos envolvendo restrições ao valor da incógnita. Por exemplo, ao resolvermos a equação 2x + 5 > 11, descobrimos que seu valor é correspondente a x > 3, de modo a respeitar a condição da inequação.
Os sinais de desigualdade podem ser utilizados em qualquer expressão matemática envolvendo incógnitas, como funções do 1º grau, do 2º grau, exponenciais, logarítmicas, trigonométricas, modulares.
As inequações também possuem gráficos representados no plano cartesiano. Na construção deles devemos levar em consideração o sinal da desigualdade.
Exemplo 1
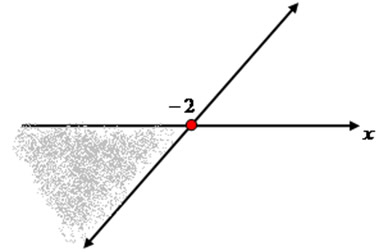
Vamos determinar a construção do gráfico da seguinte expressão: 2x + 4 ≤ 0.
y = 0
2x + 4 ≤ 0
2x ≤ – 4
x ≤ –2
Gráfico
Exemplo 2
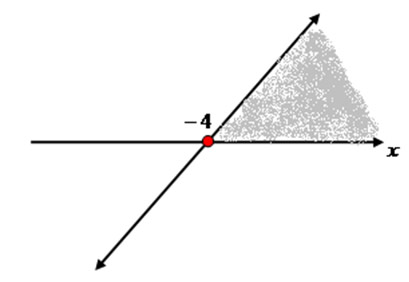
Construir o gráfico da inequação x + 4 ≥ 0, de acordo com a raiz da função.
y = 0
x + 4 ≥ 0
x ≥ – 4
Gráfico
Exemplo 3
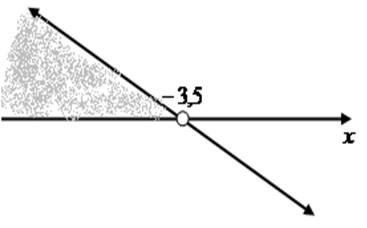
Determinando o gráfico da inequação –2x + 7 > 0.
–2x + 7 > 0
–2x > –7
x < –7/2
x < –3,5
Gráfico
Por Marcos Noé
Graduado em Matemática
>: maior que
<: menor que
≥: maior ou igual que
≤: menor ou igual que
As inequações são utilizadas em cálculos envolvendo restrições ao valor da incógnita. Por exemplo, ao resolvermos a equação 2x + 5 > 11, descobrimos que seu valor é correspondente a x > 3, de modo a respeitar a condição da inequação.
Os sinais de desigualdade podem ser utilizados em qualquer expressão matemática envolvendo incógnitas, como funções do 1º grau, do 2º grau, exponenciais, logarítmicas, trigonométricas, modulares.
As inequações também possuem gráficos representados no plano cartesiano. Na construção deles devemos levar em consideração o sinal da desigualdade.
Exemplo 1
Vamos determinar a construção do gráfico da seguinte expressão: 2x + 4 ≤ 0.
y = 0
2x + 4 ≤ 0
2x ≤ – 4
x ≤ –2
Gráfico

Exemplo 2
Construir o gráfico da inequação x + 4 ≥ 0, de acordo com a raiz da função.
y = 0
x + 4 ≥ 0
x ≥ – 4
Gráfico

Exemplo 3
Determinando o gráfico da inequação –2x + 7 > 0.
–2x + 7 > 0
–2x > –7
x < –7/2
x < –3,5
Gráfico

Por Marcos Noé
Graduado em Matemática
Ponto médio de um segmento no plano
Ponto médio de um segmento no plano
Marcelo Rigonatto
Cálculo do ponto médio
Ao contrário da reta, o segmento é finito, possuindo começo e fim, podendo ser medido. Mesmo sendo finito, ele possui infinitos pontos e o ponto que divide o segmento de reta em duas partes de mesmo tamanho é chamado de ponto médio.
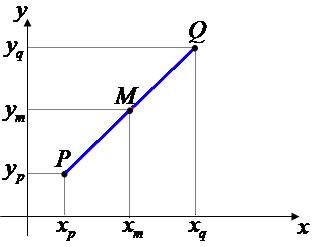
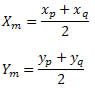
Assim, o ponto médio tem coordenadas:
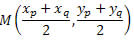
Exemplo 1. Determine as coordenadas do ponto médio do segmento AB de extremos A(1, 9) e B(7, 5).
Solução: Temos que
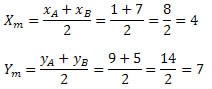
Portanto, o ponto médio do segmento AB tem coordenadas M(4 , 7)
Exemplo 2. O ponto médio do segmento PQ tem coordenadas M(5, 5). Sabendo que o ponto P tem coordenadas P(3, 4), quais são as coordenadas do ponto Q?
Solução: Sabemos que
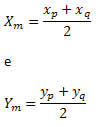
Segue que
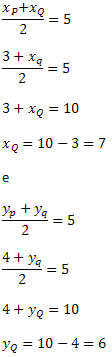
Portanto, o ponto Q tem coordenadas (7, 6).
Exemplo 3. Determine as coordenadas do ponto médio do segmento AM, sabendo que M é o ponto médio do segmento AB, sendo A(0, 0) e B(– 12, 20).
Solução: Primeiro determinaremos as coordenadas do ponto M. Como M é ponto médio do segmento AB, temos que:
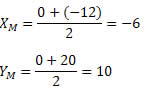
Logo, M tem coordenadas (– 6, 10).
Queremos determinar o ponto médio do segmento AM. Vamos chamar esse ponto de N. Assim,
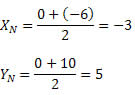
Portanto, o ponto médio do segmento AM tem coordenadas N(– 3, 5).
Gene - estrutura Conheça a unidade fundamental da vida
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com www.youtube.com/accbarroso1
Por que algumas pessoas têm olhos azuis e outras têm olhos castanhos? Por que a população humana apresenta variados tipos sanguíneos? Por que certas pessoas apresentam doenças congênitas?
As respostas a essas questões estão relacionadas aos genes, estruturas presentes em nossas células, responsáveis pelo controle de nossas características e pelo funcionamento do nosso organismo. Para entender como os genes funcionam e realizam esse controle é importante conhecermos a sua estrutura.
Genes e ácidos nucléicos
Os ácidos nucléicos são substâncias presentes em nossas células. Elas receberam esse nome pelo fato de terem sido, inicialmente, descobertas no núcleo, embora se saiba atualmente que também podem ser encontradas em outras organelas, como as mitocôndrias e os cloroplastos.
Existem dois tipos de ácidos nucléicos: o DNA (do inglês desoxirribonucleic acid ou ácido dexorribonucléico) e o RNA (do inglês ribonucleic acid ou ácido ribonucléico). Tanto a molécula de DNA como a de RNA são constituídas de unidades menores chamadas de nucleotídios.
Cada nucleotídio é formado por um grupo fosfato, um açúcar (desoxirribose no DNA e ribose no RNA) e uma base nitrogenada. Existem cinco tipos diferentes de bases nitrogenadas: timina (T), guanina (G), citosina (C) e adenina (A) são encontradas no DNA. Já no RNA, a timina é substituída por outra base, chamada de uracila (U).
Além das diferenças já citadas entre o DNA e o RNA, também é importante observar que, enquanto os nucleotídios do RNA se agrupam numa cadeia simples, a molécula de DNA apresenta duas cadeias emparelhadas e enroladas uma sobre a outra, formando uma estrutura conhecida como "dupla hélice". As cadeias do DNA emparelham-se pelas bases nitrogenadas: adenina com timina e citosina com guanina (A - T; C - G), mantendo-se unidas por pontes de hidrogênio.

Esquema das moléculas de DNA (à esquerda) e de RNA (à direita); P representa o fosfato e D (na molécula de DNA) a desoxirribose.
Os cromossomos, estruturas presentes no núcleo das células dos seres vivos em geral e no citoplasma das bactérias, são constituídos por um longo filamento de DNA associado a certas proteínas chamadas histonas. Alguns trechos do DNA presente nesses cromossomos dão início a processos de fabricação de proteínas com as mais diversas funções no organismo. Esses trechos de DNA são o que chamamos de genes.
Existem três tipos de RNA: mensageiro (RNAm), ribossômico (RNAr) e transportador (RNAt). Todos eles também participam dos processos de síntese protéica, cada um apresentando diferentes funções.
Maria Graciete Carramate Lopes
Área do retângulo
Colégio Estadual Dinah Gonçalves
Área do retângulo
Danielle de Miranda
Retângulos
Uma figura plana nada mais é que um plano que possui uma forma específica e para que ela exista é preciso que tenha no mínimo três lados. Veja abaixo a relação dos lados com a nomenclatura de algumas figuras planas.
3 lados = triângulo
4 lados = quadrilátero
5 lados = pentágono
6 lados = hexágono
7 lados = heptágono
O retângulo é um quadrilátero, pois possui 4 lados que podem ou não ser iguais. Quando os lados forem diferentes ela continua recebendo o nome de retângulo, agora quando os 4 lados forem iguais o retângulo poderá ser chamado de quadrado.
O cálculo da área desses dois tipos de retângulos é calculado da mesma forma. Como possuem duas dimensões: base e altura, o cálculo da sua área é o produto da base pela altura.
Pra compreender melhor como chegamos à conclusão de que a fórmula do cálculo da área de um retângulo é base x altura, veja a explicação abaixo:
Considere o retângulo com a superfície dividida em quadradinhos de lados iguais a um centímetro.
Nesse retângulo obtivemos 5 colunas de quadradinhos e 3 linhas de quadradinhos, assim para saber a quantidade de quadrados que essa figura possui em sua superfície basta multiplicarmos 5 x 3 = 15 quadradinhos. Como cada lado do quadradinho é igual a 1centímetro, podemos dizer que as dimensões desse retângulo são iguais a:
Aplicando o mesmo raciocínio do cálculo da quantidade de quadradinhos iremos encontrar a área da superfície desse retângulo da seguinte forma:
A = 5 cm x 3 cm
A = 15 cm2
Assim, provamos que o cálculo da área de um retângulo é:
A = BASE x ALTURA
Representando a base como b e a altura como h, simplificamos a fórmula:
A = b x h
Caso esse retângulo seja um quadrado (todos os lados iguais), podemos dizer que a base e a altura terão mesmo valor, assim iremos representá-las como sendo os lados do quadrado, representados pela letra l.
Portanto, a área de um quadrado pode ser indicada da seguinte forma:
A = l x l
A = l 2
Grafite
Por Alunos Online

O grafite, prática de fazer marcas, inscrições e desenhos em muros, surgiu no Império Romano, onde eram feitas estas manifestações artísticas, por isso o nome grafite vem do italiano “graffiti”. Contudo, o grafite só ganhou popularidade nos anos 70, no Bronx, bairro de população negra de Nova York. Assim, as pessoas queriam uma forma de comunicação entre membros de uma mesma gangue ou registro de indignação frente ao preconceito e às injustiças sociais, onde os artistas passassem a ter uma linguagem intencional para interferir na cidade.
Geralmente, os desenhos feitos nos muros retratam temas como violência, paz, amor, contrastes sociais, etc. Algumas pessoas pensam que o grafite é uma forma de vandalismo, uma vez que suja as paredes de inúmeros edifícios e, muitas vezes, edíficações históricas. No entanto, o grafite não é uma arte ilegal, pois existem locais apropriados e iniciativas que proporcionam a manifestação de forma legal e civilizada.

Grafite
Geralmente, os desenhos feitos nos muros retratam temas como violência, paz, amor, contrastes sociais, etc. Algumas pessoas pensam que o grafite é uma forma de vandalismo, uma vez que suja as paredes de inúmeros edifícios e, muitas vezes, edíficações históricas. No entanto, o grafite não é uma arte ilegal, pois existem locais apropriados e iniciativas que proporcionam a manifestação de forma legal e civilizada.
Assinar:
Comentários (Atom)







