Ângulos

Ângulos

Fonte: http://www.somatematica.com.br

ÂNGULOS ADJACENTES
Observe os exemplos de ângulos consecutivos vistos anteriormente e verifique que:

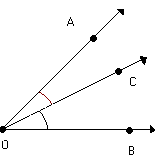	Os ângulos AÔC e CÔB não possuem pontos internos comuns
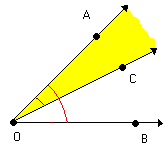	Os ângulos AÔC e AÔB possuem pontos internos comuns
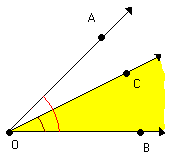	Os ângulos CÔB e AÔB possuem pontos internos comuns

Verifique que os ângulos AÔC e CÔB são consecutivos e não possuem pontos internos comuns. Por isso eles são denominados ângulos adjacentes.
Assim:

Dois ângulos são adjacentes quando são consecutivos e não possuem pontos internos comuns.

Observação:
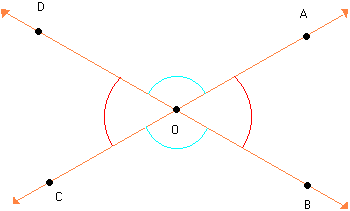
Duas retas concorrentes determinam vários ângulos adjacentes. Exemplos:

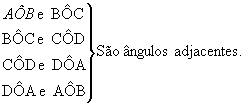
ÂNGULO AGUDO, OBTUSO E RETO

Podemos classificar um ângulo em agudo, obtuso ou reto.

• Ângulo agudo é o ângulo cuja medida é menor que 90º. Exemplo:

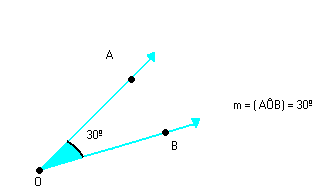
• Ângulo obtuso é o ângulo cuja medida é maior que 90º. Exemplo:

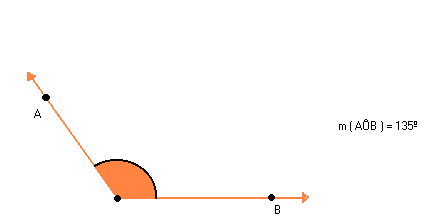
• Ângulo reto é o ângulo cuja medida é 90º. Exemplo:

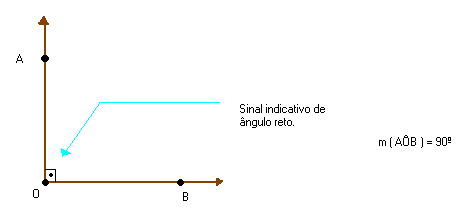
RETAS PERPENDICULARES

As retas r e s da figura abaixo são concorrentes e formam entre si quatro ângulos retos.

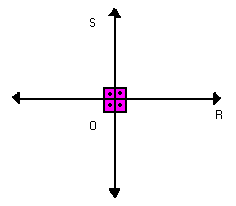
Dizemos que as retas r e s são perpendiculares e indicamos:

Observação

Duas retas concorrentes que não formam ângulos retos entre si são chamadas de oblíquos. Exemplo:

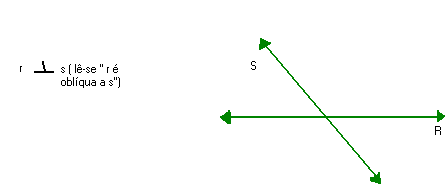
ÂNGULOS COMPLEMENTARES

Observe os ângulos AÔB e BÔC na figura abaixo:

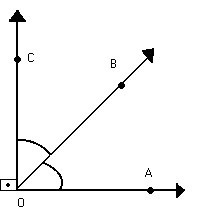
Verifique que:

m (AÔB) + m (BÔC) = 90º

Nesse caso, dizemos que os ângulos AÔB e BÔC são complementares.

Assim:

Dois ângulos são complementares quando a soma de suas medidas é 90º.

Exemplo:

Os ângulos que medem 42º e 48º são complementares, pois 42º + 48º = 90º.

Dizemos que o ângulo de 42º é o complemento do ângulo de 48º, e vice-versa.

Para calcular a medida do complemento de um ângulo, devemos determinar a diferença entre 90º e a medida do ângulo agudo dado.

Medida do ângulo	Complemento
x	90º - x

Exemplo:

• Qual a medida do complemento de um ângulo de 75º?

Solução

Medida do complemento = 90º - medida do ângulo

Medida do complemento = 90º - 75º

Medida do complemento = 15º

Logo, a medida do complemento do ângulo de 75º é 15º.

Observação:

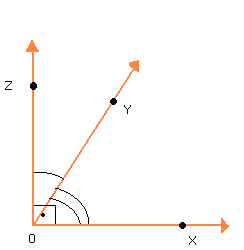
Os ângulos XÔY e YÔZ da figura ao lado, além de complementares, são também adjacentes. Dizemos que esses ângulos são adjacentes complementares.

ÂNGULOS SUPLEMENTARES

Observe os ângulos AÔB e BÔC na figura abaixo:

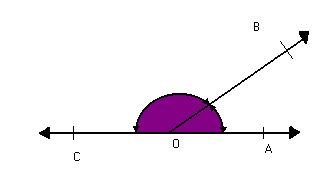
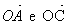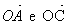As semi-retas formam um ângulo raso.

Verifique que:

m ( AÔB ) + m (BÔC) = 180º

Nesse caso, dizemos que os ângulos AÔB e BÔC são suplementares. Assim:

Dois ângulos são suplementares quando a soma de suas medidas é 180º.

Exemplo:
Os ângulos que medem 82º e 98º são suplementares, pois 82º + 98º = 180º.
Dizemos que o ângulo de 82º é o suplemento do ângulo de 98º, e vice-versa.
Para calcular a medida do suplemento de um ângulo, devemos determinar a diferença entre 180º e a medida do ângulo agudo dado.

Medida do ângulo	Suplemento
X	180º - X

Exemplo:

• Qual a medida do suplemento de um ângulo de 55º?

Solução
Medida do suplemento = 180º - medida do ângulo
Medida do suplemento = 180º - 55º
Medida do suplemento = 125º
Logo, a medida do suplemento do ângulo de 55º é 125º.
Observação:

Os ângulos XÔY e YÔZ da figura ao lado, além de suplementares, são também adjacentes. Dizemos que esses ângulos são adjacentes suplementares.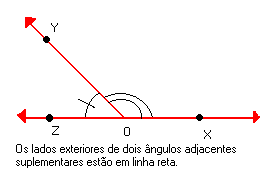

ÂNGULOS OPOSTOS PELO VÉRTICE
Observe os ângulos AÔB e CÔD na figura abaixo:

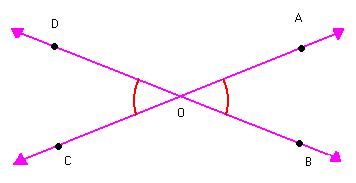
Verifique que:

Nesse caso, dizemos que os ângulos AÔB e CÔD são opostos pelo vértice (o.p.v). Assim:

Dois ângulos são opostos pelo vértice quando os lados de um deles são semi-retas opostas aos lados do outro.

Na figura abaixo, vamos indicar:

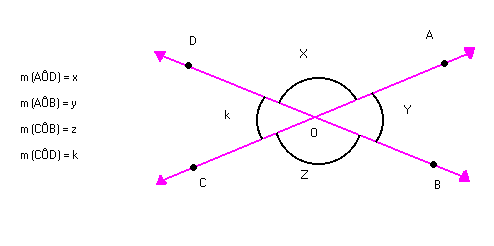
Sabemos que:

X + Y = 180º ( ângulos adjacentes suplementares)

X + K = 180º ( ângulos adjacentes suplementares)

Então:

Logo: y = k

Assim:

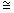m (AÔB) = m (CÔD) AÔB CÔD

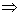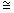m (AÔD) = m (CÔB) AÔD CÔB

Daí a propriedade:

Dois ângulos opostos pelo vértice são congruentes.

Observe uma aplicação dessa propriedade na resolução de um problema:

• Dois ângulos opostos pelo vértice têm medidas, em graus, expressas por x + 60º e 3x - 40º. Qual é o valor de x?

Solução:

x + 60º = 3x - 40º ângulos o.p.v x - 3x = - 40º - 60º -2x = - 100º x = 50º Logo, o valor de x é 50º.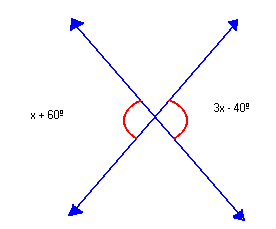

EQUAÇÕES IRRACIONAIS

EQUAÇÕES IRRACIONAIS Definição: Chama-se equação irracional a equação cuja, incógnita está sob radical. Exemplos:

EXERCÍCIOS 1) Quais são as equações irracionais.

RESOLUÇÃO DE EQUAÇÕES IRRACIONAIS Na resolução da equações irracionais em R, procedemos do seguinte modo: 1º - Isolamos um dos radicais em um dos membros da equação dada. 2º - Elevamos os dois bembros da equação a um expoente adequado. 3º - Se ainda restar um ou mais radicais, repetimos as operações anteriores. 4º - Verificar as soluções encontradas. . RAÍZES ESTRANHAS Quando se elevam os dois membros de uma equação a um mesmo expoente par, a equação obtida tem, raízes estranhas à equação original. veja: A equação x = 5 tem como conjunto V = {5} Elevando ambos os membros ao quadrado, vamos ter x² = 25 cujo o conjunto verdade é V - {5, -5} Concluindo: Na resolução de uma equação irracional com radical de indice par, devemos fazer uma verificação da validade da raizes encontradas na equação original e eliminar as raízes estranhas. Mostraremos a resolução de equações irracionais no conjunto R.

EXERCÍCIOS 1) Resolva as equações irracionais em R:

2) Resolva as equações irracionais em R.

3) Resolva as equações irracionais em R

1) Resolva as equações irracionais em R:

Exercícios:

As Leis de Newton

Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso

Colégio Estadual Dinah Gonçalves

email accbarroso@hotmail.com

 www.ensinodematemtica.blogspot.com.br

www.accbarrosogestar.blogspot.com.br 

      

Isaac Newton propôs as leis que descrevem o comportamento dos corpos em movimento.

Galileu deixou várias contribuições científicas para a humanidade, como a difusão do modelo heliocêntrico de Copérnico e a invenção de alguns tipos de lunetas. Algumas de suas descobertas serviram de referência para que Isaac Newton criasse as bases da mecânica com três leis fundamentais.

Inércia

Inércia é a tendência que os corpos apresentam de permanecer no seu estado de equilíbrio, em repouso ou em movimento retilíneo e uniforme.

Podemos perceber essa tendência quando observamos uma pessoa que está em pé dentro de um ônibus. Caso o motorista pise no acelerador, fazendo com que o ônibus arranque, o passageiro que está em pé, por inércia, tende a continuar parado em relação ao solo terrestre.

Agora, como o ônibus está em movimento, se o motorista frear, a tendência do passageiro é continuar em movimento em relação ao solo terrestre, fato este que não acontece por estar se segurando na barra de apoio do ônibus.

Primeira Lei de Newton

Também conhecida como a lei da inércia, trata a respeito das condições de equilíbrio das partículas. Uma partícula pode ou não receber a ação de várias forças. Se a soma vetorial desses vetores-força for nula, dizemos que a partícula está em equilíbrio.

Massa: é a medida quantitativa da inércia de um determinado corpo. Então, quanto maior a massa de um corpo, maior vai ser a dificuldade para vencer a inércia desse corpo.

Segunda Lei de Newton

Na segunda lei, Newton analisou a relação que existe entre a força aplicada em um corpo e a mudança na velocidade que ele sofre. Após realizar várias experiências, Newton constatou que algo sempre ocorria.

A variação da velocidade sofrida por um corpo é diretamente proporcional à resultante das forças nele aplicadas.

Então, quando há variação de velocidade, em um determinado intervalo de tempo, encontramos a aceleração desse corpo.

F_r = m.a – força resultante é igual ao produto da massa pela aceleração.

As unidades, no SI, são: N (newton) para força, kg para m e m/s² para a.

Terceira Lei de Newton

Vamos agora considerar uma mesa bem lisa. Sobre ela temos um bloco de ferro e um ímã bem próximos um ao outro, como mostra a figura abaixo.

Mantendo o ímã fixo, se abandonarmos o bloco de ferro, ele será atraído pelo ímã, deslocando-se para a esquerda.

Mantendo o ferro fixo, se abandonarmos o ímã, ele será atraído pelo ferro, deslocando-se para a direita.

Ao analisar casos parecidos com esse que citamos, Newton enunciou a terceira lei, que também é conhecida como lei da ação e reação. De acordo com Newton, não existe força que seja capaz de agir sozinha, pois, para cada força considerada ação, existe outra chamada de reação.

Temos que lembrar que as forças de ação e reação ocorrem sempre em corpos distintos e por isso não se anulam mutuamente.

Por Domiciano Marques

Tronco de pirâmide

Tronco de pirâmide de bases paralelas

Ao cortarmos as arestas laterais de uma pirâmide por um plano semelhante à base, que não inclui esta e nem o vértice, adquirimos uma secção poligonal, onde:



1) A razão semelhança é dada pela divisão das arestas laterais e da altura.




2) O plano limitado da secção e a base são idênticos.

3) A relação entre as superfícies da secção (As) e a base (AB) é idêntico ao quadrado da razão de semelhança.

4) O tronco da pirâmide de bases paralelas está situado entre a base e à secção da mesma.

5) A relação entre o volume e a base (AB) e (As) é igual ao cubo da razão de semelhança.

extraido de www.colegioweb.com.br

Ciclo Trigonométrico função cotangente aula 6

Determinantes Matriz de ordem 3 Sarrus e Laplace aula 2

Análise Combinatório Permutação aula 5

Poluição

O uso indevido do solo e a má gestão dos resíduos urbanos e rurais.

A constante ação humana no meio ambiente provoca vários desequilíbrios ambientais, seja afetando os cursos hídricos, o ar atmosférico ou degradando os solos, interferindo diretamente nas relações ecológicas da fauna e flora.

Altamente degradável, o solo é um meio bastante afetado pela pressão antrópica. Sua poluição afeta particularmente o nível superficial da crosta terrestre, camada da biosfera que abriga considerável biodiversidade.

Esse meio, diferente do que pensamos, não é inerte e tampouco sustenta apenas as relações humanas. No extrato superficial do solo habitam espécies de macro e microorganismos importantes à manutenção do equilíbrio biológico no planeta: bactérias, fungos, nematódeos, artrópodes, anelídeos, moluscos e pequenos vertebrados, aliados à vegetação, dão vida e sustentação a esse substrato.

No entanto, exposta aos mais variados tipos de impactos, prejudicam as formas viventes e o seu “pleno” desenvolvimento regular.

A poluição do solo, dependendo da magnitude, pode causar malefícios irreparáveis tanto à natureza, que responde lentamente aos processos de reparação, quanto à frágil estrutura corpórea do homem.

Sendo o homem o agente causador, a origem poluidora dos solos pode ser urbana ou rural, refletindo os danos característicos em cada meio de ocupação humana.

Em áreas urbanas o principal problema é a enorme quantidade de lixo lançado sobre a superfície aliada à falta de tratamento.

Detritos domésticos, hospitalares, industriais, dentre outras substância, como produtos químicos derivados do petróleo e chumbo, são despejados na natureza sem o mínimo controle ambiental e sanitário. Além de acumular no ambiente, dependendo da degradabilidade do dejeto, pode interferir organicamente nos níveis tróficos ecológicos.

Nas áreas rurais, a contaminação do solo, ocorre exclusivamente pelo uso inadequado e abusivo de agrotóxicos e fertilizantes. O DDT, inseticida largamente utilizado nas lavouras para eliminar insetos, atualmente proibido em vários países, é uma substância com alta capacidade de retenção no solo e nos tecidos e órgãos dos animais.

Essa substância desencadeia sérios danos à saúde de animais e dos seres humanos, pode causar problemas dermatológicos, hepáticos e até o desenvolvimento de um câncer.

Dessa forma, diante de toda a problemática que envolve a gestão de resíduos urbanos e utilização de defensivos agrícolas, merece esse assunto maior atenção governamental na aplicação e implementação constitucional em defesa da preservação ambiental, bem como a responsabilidade social da população.

Relações Métricas no Triângulo Retângulo aula 1

Vitaminas Propriedades e funções dos micronutrientes

Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso

Colégio Estadual Dinah Gonçalves

email accbarroso@hotmail.com

 www.ensinodematemtica.blogspot.com.br

www.accbarrosogestar.blogspot.com.br 

       

O organismo humano é uma máquina biológica complexa, com inúmeros órgãos e sistemas trabalhando em sincronia. E, semelhante a um carro - que, se não estiver abastecido, não funciona e de nada adianta toda a tecnologia utilizada na sua fabricação -, necessita de combustível para manter-se em pleno funcionamento.

No caso do corpo humano, o combustível é denominado nutriente e pode ser encontrado nos alimentos.

Os nutrientes são classificados em macronutrientes e micronutrientes. Os carboidratos, proteínas, gorduras e fibras alimentares são considerados macronutrientes, pois são necessários em grandes quantidades na dieta diária de um indivíduo.

Micronutrientes
Quanto aos micronutrientes, são substâncias que devem ser diariamente ingeridas, em pequenas quantidades, suficientes para exercerem suas funções. São os sais minerais, a água e as vitaminas.

As vitaminas são adquiridas exclusivamente pela dieta diária do ser humano, já que nosso metabolismo é incapaz de produzi-las. Esses compostos possuem múltiplas funções, porém, em sua grande maioria, atuam como cofatores em reações químicas mediadas por enzimas.

Portanto, se a dieta de uma pessoa não for rica em vitaminas, algumas enzimas deixam de atuar adequadamente, gerando um quadro clínico denominado avitaminose.

As vitaminas A, D, E e K são classificadas como lipossolúveis, pois só podem ser absorvidas pelas paredes internas do intestino se houver a presença de lipídeos, ou seja, óleos e gorduras.

Já as vitaminas C e do complexo B são classificadas como hidrossolúveis, pois sua absorção ocorre quando há presença de água.

Vitaminas hidrossolúveis
O complexo B é um conjunto de oito vitaminas simbolizadas pela letra "B". Essas vitaminas possuem múltiplas funções, sendo que suas ações estão diretamente ligadas à regulação do metabolismo celular.

A tiamina (vitamina B1) é um composto encontrado em cereais, feijão, fígado, carne de porco, ovos e vegetais em folha (verduras). Essa vitamina auxilia na quebra de carboidratos para obtenção de energia, atua no bom funcionamento do sistema nervoso, além de estimular o apetite e manter o tônus muscular. A falta de vitamina B1 resulta em um quadro de falta de apetite e nervosismo, além de possibilitar o surgimento de beribéri, doença que provoca fadiga muscular e dificuldades respiratórias.

A vitamina B2, denominada riboflavina, atua na coordenação motora, sendo essencial no processo de respiração celular. Ela mantém a tonalidade saudável da pele. Pode ser ingerida quando nos alimentamos de couve, repolho, espinafre, carnes magras, ovos, fígado e leite. Quando ingerimos quantidade insuficiente desse composto, há o surgimento de aftas (úlceras) nas mucosas dos lábios, língua e bochechas.

Se o indivíduo está desanimado, com falta de energia para as atividades cotidianas, fica nervoso ao extremo com facilidade e tem distúrbios digestivos, pode ser que esteja ingerindo quantidade insuficiente de ácido nicotínico, também conhecido como vitamina B3. Esta vitamina pode ser encontrada no levedo de cerveja, nas carnes magras e também em ovos, fígado e leite. Ela mantém o tônus muscular e nervoso e atua no bom funcionamento do sistema digestório.

O ácido pantolênico (vitamina B5) é encontrado em carnes de forma geral, leite e derivados, verduras e cereais integrais. A vitamina B5 atua em processos energéticos das células - e sua falta provoca anemia, fadiga muscular e dormência nos membros.

Quando ingerimos leite, cereais integrais, carnes magras ou fígado estamos realizando uma dieta rica em vitamina B6 (piridoxina). A ingestão dessa vitamina em quantidades corretas traz benefícios para a pele e o sistema nervoso central.

A vitamina B8, ou seja, a Biotina, também está relacionada à manutenção da pele e ao bom funcionamento neuromuscular. Esta vitamina pode ser encontrada em alimentos - como carnes, legumes, verduras - e nas bactérias da flora intestinal.

Quando nos ferimos, a vitamina B9 entra em ação. O ácido fólico é importante na síntese das bases nitrogenadas e, portanto, na síntese de DNA e na multiplicação celular para o reparo do ferimento. As principais fontes vitamínicas do ácido fólico são os vegetais verdes, frutas e bactérias da flora intestinal. Alguns casos de anemia e esterilidade masculina ocorrem pela falta dessa vitamina.

A anemia perniciosa é causada pela avitaminose de cianocobalamina, ou seja, falta de vitamina B12. Carne, ovos, leite e seus derivados são as principais fontes alimentares dessa vitamina. A falta de cianocobalamina também pode causar distúrbios nervosos.

O ácido ascórbico ou vitamina C é a mais popular das vitaminas. Previne infecções de forma geral e o escorbuto. Pode ser encontrada em frutas cítricas (como limão, laranja e acerola) e também no tomate, na couve, no repolho e no pimentão. Quando o indivíduo não a ingere em quantidade suficiente pode desenvolver insônia, inércia e fadiga (falta de energia), dores nas articulações e sangramento das gengivas.

Vitaminas lipossolúveis
O retinol ou vitamina A está relacionada com o crescimento normal do indivíduo, prevenindo contra várias infecções e evitando a cegueira noturna (xeroftalmia). A vitamina A é encontrada em vegetais amarelos (cenoura, milho e abóbora), pêssego, nectarina, gema do ovo de galinha, manteiga e fígado.

A vitamina D (calciferol) não é encontrada pronta na maioria dos alimentos. Vegetais verdes, tomate e castanhas possuem uma substância precursora de vitamina D que, quando entra em contato com a radiação solar, é convertida em calciferol. Atua no metabolismo do cálcio e fósforo, mantendo a estrutura de ossos e dentes saudável. A deficiência de vitamina D promove o estabelecimento do raquitismo. Pode ser encontrada em fígado, olho de fígado de bacalhau e gema de ovo.

Além da vitamina D, podemos encontrar outra vitamina em vegetais verdes, tomate e castanha: a filoquinona. É comumente denominada vitamina K e previne hemorragias, atuando na coagulação sanguínea.

Finalmente, a vitamina E. O óleo de germe de trigo, as carnes magras, a alface e o óleo de amendoim são fontes ricas em vitamina E. O tocoferol promove a fertilidade, atuando no sistema nervoso involuntário, no sistema muscular e nos músculos que realizam contrações involuntárias. A falta dessa vitamina provoca a esterilidade e o aborto.

Portanto, as vitaminas são, de fato, micronutrientes, já que são detectadas em pequenas quantidades no organismo humano. Porém, sua participação no funcionamento e na regulação do nosso metabolismo é imprescindível, tornando-as substâncias de alta significância fisiológica.
*Rodrigo Luís Rahal é bacharel e licenciado em biologia, mestre em Biologia Celular e Estrutural pela UNICAMP e professor do curso de Ciências Biológicas do Centro Universitário São Camilo em São Paulo.

Estudo da reta

Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso

Colégio Estadual Dinah Gonçalves

email accbarroso@hotmail.com        

 www.ensinodematemtica.blogspot.com.br

www.accbarrosogestar.blogspot.com.br 

      

ESTUDO DA RETA

COEFICIENTE ANGULAR OU DECLIVIDADE DE UMA RETA

Coeficiente angular (m) de uma reta r não perpendicular ao eixo das abscissas é o número real m que expressa a tangente trigonométrica de sua inclinação , ou seja:

m = tg


EQUAÇÃO DA RETA

Equação geral da reta

Toda reta do plano possui uma equação da forma:

ax + by + c = 0

na qual a, b, c são constantes e a e b não simultaneamente nulos.

Exemplos:

a) – 5x + 3y - 1 = 0

b) 9x – 4y – 13 = 0

Equação reduzida da reta

É toda equação de reta onde a variável y fica isolada. Na equação da reta na forma reduzida podemos identificar o coeficiente angular do lado da variável x e o coeficiente linear (termo independente da equação).

Exemplos:

a) y = 8x – 10

Coeficiente angular = 8

Coeficiente linear = - 10

b) y = – 4x + 12

Coeficiente angular = – 4

Coeficiente linear = 12

CÁLCULO DO COEFICIENTE ANGULAR E DA EQUAÇÃO DA RETA

Para calcular o coeficiente angular (não possuindo o valor da inclinação ) e achar a equação da reta, utiliza-se uma única fórmula:

Importante: A partir da fórmula acima, podemos determinar o coeficiente angular e a equação da reta da seguinte forma:


Coeficiente angular Equação da reta

2 valores para o y. O valor do m.

2 valores para o n. 1 valor para o n.

1 valor para o x.

Aplicação

Determine a equação da reta que passa pelos A (4, 12) e B (0, 4)

Solução:


1.º passo (cálculo do m – 2 valores para o y e 2 para o x):



2.º passo (equação da reta – o valor do m, 1 valor de y e um valor de x):,