Introdução:
O ciclo da cana-de-açúcar foi a primeira atividade economicamente organizada do Brasil. A partir da fundação do primeiro engenho de cana-de-açúcar pelo Sr Martins Afonso de Souza, em 1532, e por mais de dois séculos o açúcar foi o principal produto brasileiro, convivendo, contribuindo e, às vezes, resistindo às mudanças sócio-politico-culturais deste período.
Este estudo visa resgatar o período de reinado do açúcar, enquanto “embaixador” do Brasil, colônia portuguesa recém descoberta e sem maior expressividade ou mesmo importância econômica, na Europa dos séculos XVI a XIX.
Serão enfocados, neste trabalho, características como motivo, facilitadores, dificultadores, pressões, conflitos e conseqüências decorrentes do ciclo da cana-de-açúcar.
A necessidade de colonizar a terra para defendê-la e explorar suas riquezas fizeram com que o Governo de Portugal instalasse engenhos produtores de açúcar no nosso litoral, essa cultura foi escolhida por se tratar de um produto de alto valor no comércio europeu e por seu consumo crescente na Europa.
Logo, após as dificuldades de sua implantação - a falta de dinheiro para montar a moenda, comprar escravos, refinar o açúcar e sobretudo transportá-lo nos mercados consumidores da Europa - o açúcar tornou-se o principal produto brasileiro e foi a base de sustentação da economia e da colonização do Brasil durante os século XVI e XVII.
Já no século XVIII o surgimento do açúcar de beterraba e a formação dos conhecimentos e técnicas para construção de uma indústria açucareira por parte dos holandeses fizeram com que nosso principal produto entrasse em decadência e perdesse mercado consumidor na Europa. Assim, acabaria o monopólio do açúcar e alteraria o quadro político-econômico da época em nosso país.
Surgimento da Economia Açucareira:
No início da colonização Brasileira o governo metropolitano resolveu estimular alguns portugueses a instalarem engenhos para produzirem açúcar no litoral do Brasil. Era preciso efetivar a aposse da terra para defendê-la e também explorá-la em suas riquezas. Optou-se pela cana de açúcar por se tratar de uma cultura rápida, chegando ao corte a partir do segundo ano e também devido ao tipo de solo existente, o massapé excelente para o plantio de cana. Além disso o Nordeste, por sua localização estratégica, permitia fácil escoamento do açúcar produzido estando mais próximo dos mercados consumidores. Outro fator que contribuiu na decisão de cultivar a cana, foi o preço do açúcar alcançado no comércio europeu.
O consumo do açúcar , em ascendência na Europa, logo seria o principal produto Brasileiro - séculos XVI e XVII - tornando o açúcar a base de sustentação da economia e da colonização do Brasil durante estes períodos.
A utilização do açúcar como adoçante, em substituição ao mel, causou na Europa do século XVI uma revolução comportamental e comercial uma vez que o produto era usado anteriormente apenas como remédio. Esse Fato destacou o Brasil, como grande produtor de açúcar, no mercado europeu.
A cultura da cana de açúcar propiciava aos donatários de terras da ocupação das mesmas pois povoados se formavam em torno dos engenhos. O primeiro engenho foi instalado por Martins Afonso de Souza, em 1532.
Foram grandes as dificuldade encontradas para desenvolver o ciclo do açúcar, tais como: dinheiro para montar as moendas, comprar escravos, transportar os colonos brancos, comprar navios para transportar os equipamentos e sustentar os trabalhadores até que a produção do açúcar desse lucro, além da preocupação com o refino e comercialização do produto.
Os holandeses surgem, então, como financiadores, transportadores e negociadores do nosso açúcar no mercado consumidor europeu. Podemos dizer que foram os holandeses o maiores beneficiados de forma lucrativa com o nosso açúcar.
A produção do açúcar no brasil se tornou motivo de grandes invasões, como as holandesas ocorrida em Pernambuco, maior produtor de açúcar. Estas invasões resultaram em grande perda de engenhos, muitos destruídos, causando um retrocesso na economia, que logo se recuperou pois o declínio da mineração, no final do de século XVII, permitiu um novo florescimento da economia açucareira, não só em Pernambuco, e na Bahia onde era tradicional, mas também na região de Campos e em algumas zonas de São Paulo. Essa economia teve como classe dominante os grandes proprietários senhores de engenho, que eram também os donos de escravos (classe dominada) e os donos do poder.
Desenvolvimento da Economia Açucareira:
Os centros urbanos que se desenvolveram em áreas especializadas na cultura da cana e no fabrico do açúcar foram, no Brasil, os pontos que se tornaram os mais desenvolvidos em valores da nossa cultura moral, intelectual, religiosa, científica e artística.
Em 1560, Portugal ganhava ascendência no comércio europeu, com o açúcar fabricado no Brasil. Com o êxito do açúcar no comércio, o governo português incentivou a expansão das fábricas em sua colônia tropical americana. Com isso Portugal estava, com estímulos oficiais, desenvolvendo a economia brasileira. Lavoura extensivas de cana-de-açúcar surgiram para alimentar os engenhos. Estes por sua vez eram instalados à beira-mar ou nas proximidades dos rios por necessidade não só de seu funcionamento como também pela questão de transporte do produto. Ao lado do canavial, nascia a agricultura de subsistência, para atender a crescente necessidade de alimentos para a casa grande, a senzala e a pequena parcela de assalariados livres. A propriedade rural, verdadeiro feudo, era, então, assim formada:
A casa-grande onde vivia o senhor com sua família, exercendo grande autoridade sobre todos. Era um verdadeiro patriarca.
A senzala era uma grande construção onde os negros escravos viviam miseravelmente, tratados como animais e sujeitos a toda a sorte de violência e castigos.
A capela onde se realizavam as cerimônias religiosas. Além, de centro religioso, a capela era um centro social, pois nela se reuniam todos os homens livres do engenho e das proximidades.
E a moenda, onde a cana-de-açúcar era moída. O caldo corria da moenda para os tachos por meio de calhas. Dos tachos, o caldo era retirado em vasilhas de cobre e levado para a caldeira, onde era fervido e mexido pelos escravos, que tiravam as impurezas e a espuma.
O rápido desenvolvimento da indústria açucareira, fez com que o governo português não se limitasse só a fabrica de moenda e engenho de água, mais numa busca rápida desta lavoura, graças à uma abundante mão-de-obra indígena existente já nas colônias deste século ligada a essa atividade. O começo da colonização se deu em pequenas comunidades que teve importante papel na especialização de mão-de-obra dos escravos. Logo depois veio a mão-de-obra dos escravos africano, que chegou para a expansão da empresa, quando os lucros já se encontravam assegurados. Era um sistema de produção rentável e capitalizado.
Durante o ciclo do açúcar ocorreu a ocupação Holandesa no Brasil. Desde o início do ciclo do açúcar, notava-se o interesse comum entre portugueses e flamengos. Logo após a ocupação holandesa em 1580, os flamengos começaram a trabalhar em Pernambuco registrando-se uma exportação de 512.273 arrobas de açúcar branco, mascavo e “de panela”. Foram também os Holandeses que trouxeram as moedas metálicas para o Brasil.
Durante o domínio holandês foi estimulada a imigração, para Pernambuco e capitanias vizinhas, de europeus qualificados como senhores de engenho ou agricultores, entre eles muitos judeus ricos, oriundos da Holanda, da Alemanha, da Hungria e da Polônia, os quais também adquiriram seus engenhos.
Quando Portugal conseguiu finalmente expulsar os flamengos, que haviam passado a dominar o processo de fabricação do açúcar, estes foram para as Antilhas e lá desenvolveram a produção do açúcar. Assim, Brasil e Antilhas assumiram, durante os séculos XVII e XVIII, o papel de abastecedores de açúcar para o mercado europeu.
Desarticulação da Economia Açucareira:
Quando Portugal foi absorvido pela Espanha modificou-se profundamente o quadro político-econômico do Brasil, surgindo o interesse da Holanda em controlar o comércio do açúcar. Desse interesse surge uma guerra sem quartel contra a Espanha. Como efeito dessa guerra temos o controle, por parte dos holandeses, do transporte e comercialização de açúcar na Europa do século XVII.
Do século XVIII ao XIX o açúcar continuou a ter importância na economia do nosso país, embora o café viesse a se tornar o principal produto brasileiro. Mas pouco a pouco o açúcar perdeu mercado e foi deixando de ser a base de sustentação da nossa economia.
Outros acontecimentos que prejudicaram o açúcar brasileiro foram o Bloqueio de Napoleão Bonaparte contra os navios ingleses transportadores de açúcar do nosso continente para o mercado consumidor europeu e o aparecimento do açúcar de beterraba, o chamado “açúcar alemão”. Esse novo produto foi utilizado pelos países consumidores como um produto substituto ao açúcar da cana, ocorrendo o agravamento da crise do nosso açúcar e os maus efeitos decorrentes da monocultura latifundiária em nossa economia.
Com todos esses problemas e com o descaso do Governo de Portugal em relação a sua colônia ocorreu a desarticulação da economia açucareira no Brasil, isso tendo como forte aliado: o preconceito em relação ao clima e a relação de inferioridade do nosso povo. Em suma, alimentávamos, em relação a nós próprios, praticamente todos os preconceitos e aprendemos a valorizar e admirar o alheio, o que é estrangeiro, e menosprezar o que é nosso, chegando a ter vergonha de nós mesmos.
Encerramento da Economia Açucareira:
A guerra realizada pela Holanda contra a Espanha modificou a nossa colonização, os grandes beneficiados foram os holandeses que passaram a ter praticamente todo o comércio dos países europeus realizado por mar, pois, era o meio de transporte mais rápido e importante da época. Sendo que, no Brasil, os batavos detiveram o controle da produção do açúcar, sendo um grande modificador para nossa economia.
Os holandeses, enquanto estiveram no Brasil, adquiriram todo o conhecimento de técnicas e organizações da indústria açucareira, pois, era isso o que eles precisavam para implantarem uma nova base industrial. A partir desse momento, estaria perdido o monopólio e alterado os dois grupos representativos da época, os portugueses produtores e os holandeses financiadores.
Assim, a partir de meados do século XVIII e durante todo o século XIX, o preço do açúcar permaneceu reduzido à metade. Sem recursos próprios para conter a desvalorização do açúcar o Governo de Portugal e os produtores portugueses mudam atenção para o café, no século XIX.
Dessa forma houve no próprio funcionamento do ciclo do açúcar, elementos negativos que impediram sua viabilidade ao progresso. Ocorrendo, então, o encerramento do monopólio da economia açucareira que manteve sua importância, porém deixou de ser o principal produto e a base de sustentação da economia brasileira.
A essa altura já se ia encerrando o ciclo do açúcar tendo como conseqüência o êxodo da população para a região de mineração no interior do Brasil.
Conclusão:
A cultura do açúcar surgiu, no Brasil, pela necessidade de colonizar a terra, para defendê-la e para explorar suas riquezas.
A importância dessa cultura pode ser exemplificada pelo interesse dos holandeses, que atravessaram mares para invadir Pernambuco, à época maior produtor de açúcar. Mesmo quando expulsos, os holandeses não abandoaram a produção de açúcar. Optaram pela transferência do know how do cultivo da cana e refino do produto para as Antilhas que, ao lado do Brasil, dominaram o comércio de açúcar na Europa nos séculos XVII e XVIII.
Embora essa cultura tenha sido responsável pela base de sustentação da economia e da colonização do nosso país durante os século XVI e XVII, o governo português não assegurou à sua colônia condições para manutenção do monopólio sobre seu domínio, que primeiro passa aos holandeses e posteriormente é compartilhado com os mesmos.
Também contribui para o declínio do produto a perda de importância do mesmo no mercado europeu em decorrência ao surgimento do açúcar de beterraba.
Assim, no século XIX, o açúcar deixa de ser principal produto nacional papel que passa, então, a ser exercido pelo café.
Autoria: Fabíola Schwartz
Esse é o blog do Professor de Matemática Carlos Barroso. Trabalho no Colégio Estadual Dinah Gonçalves . Valéria-Salvador-Bahia .Inscreva-se Já no meu canal www.youtube.com/accbarroso1 e receba as videoaulas de Matemática.
terça-feira, 7 de abril de 2020
Progressão aritmetica
É fácil encontrar exercícios sobre progressões que envolvam ao mesmo tempo a progressão geométrica e aritmética, ou seja, que em um mesmo exercício seja preciso utilizar os conceitos das duas progressões.
Veja um exemplo de como essa junção pode acontecer.
A seqüência (8 , 2 , a , b , ...) é uma P.G e a seqüência (b , 3/16 , c , ...) é uma P.A.
a) Qual é o valor de c?
Primeiro é preciso levar em consideração a P.G.
(8 , 2 , a , b , ...) a sua razão será igual a q = 2/8 = 1/4, dessa forma é necessário prosseguir dizendo que:
a : 2 = 1/4 → a = 1/2
a : b = 1/4 → 1/2 : b = 1/4 → b = 1/8
Com os valores de a e b, pode-se levar em consideração a P.A para que seja possível encontrar o valor do termo c.
(b , 3/16 , c , ...) substituindo o valor de b na P.A teremos:
(1/8 , 3/16 , c , ...), dessa forma, a razão dessa P.A será: r = 3/16 – 1/8 = 1/16.
Com o valor da razão podemos dizer que:
c – 3/16 = r
c – 3/16 = 1/16
c = 1/16 + 3/16
c = 1/4
www.mundoeducacao.com.br
Veja um exemplo de como essa junção pode acontecer.
A seqüência (8 , 2 , a , b , ...) é uma P.G e a seqüência (b , 3/16 , c , ...) é uma P.A.
a) Qual é o valor de c?
Primeiro é preciso levar em consideração a P.G.
(8 , 2 , a , b , ...) a sua razão será igual a q = 2/8 = 1/4, dessa forma é necessário prosseguir dizendo que:
a : 2 = 1/4 → a = 1/2
a : b = 1/4 → 1/2 : b = 1/4 → b = 1/8
Com os valores de a e b, pode-se levar em consideração a P.A para que seja possível encontrar o valor do termo c.
(b , 3/16 , c , ...) substituindo o valor de b na P.A teremos:
(1/8 , 3/16 , c , ...), dessa forma, a razão dessa P.A será: r = 3/16 – 1/8 = 1/16.
Com o valor da razão podemos dizer que:
c – 3/16 = r
c – 3/16 = 1/16
c = 1/16 + 3/16
c = 1/4
www.mundoeducacao.com.br
Moda e mediana
Ao realizar uma pesquisa é aconselhável realizar um estudo estatístico dos dados apresentados. Através desse estudo podemos tirar as conclusões necessárias sobre o universo pesquisado. A estatística descritiva é a parte da estatística responsável por realizar essa análise, apontando tendências de comportamento das variáveis, criando gráficos e descrevendo as características dos conjuntos pesquisados.
Numa pesquisa, os dados tendem a se concentrar em torno dos valores centrais. Esses valores centrais são chamados de medidas de tendência central. São elas: Média, Moda e Mediana. Iremos abordar e conceituar Moda e Mediana.
Definição de Moda (Mo): é o valor que mais aparece num conjunto de dados.
Exemplo 1. Os dados abaixo se referem à idade de 20 alunos de uma turma de 6º ano.
Idade: {12, 11, 12, 13, 12, 11, 13, 12, 12, 11, 14, 13, 13, 12, 11, 12, 13, 14, 11, 14}
A moda desse conjunto de dados será a idade que mais aparece, ou seja:
Mo = 12 (pois é a idade que aparece mais vezes no conjunto)
Exemplo 2. A tabela abaixo apresenta as notas em matemática de uma turma de 30 alunos.
Numa pesquisa, os dados tendem a se concentrar em torno dos valores centrais. Esses valores centrais são chamados de medidas de tendência central. São elas: Média, Moda e Mediana. Iremos abordar e conceituar Moda e Mediana.
Definição de Moda (Mo): é o valor que mais aparece num conjunto de dados.
Exemplo 1. Os dados abaixo se referem à idade de 20 alunos de uma turma de 6º ano.
Idade: {12, 11, 12, 13, 12, 11, 13, 12, 12, 11, 14, 13, 13, 12, 11, 12, 13, 14, 11, 14}
A moda desse conjunto de dados será a idade que mais aparece, ou seja:
Mo = 12 (pois é a idade que aparece mais vezes no conjunto)
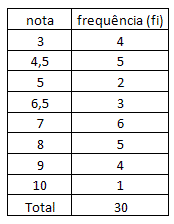
Exemplo 2. A tabela abaixo apresenta as notas em matemática de uma turma de 30 alunos.

Na coluna da esquerda temos as notas na disciplina de matemática e na coluna da direita, quantos alunos obtiveram a respectiva nota. Dessa forma, podemos observar que a nota que mais aparece nesse conjunto de dados é 7. Portanto,
Mo = 7.
Exemplo 3. Os dados abaixo são referentes ao número dos calçados vendidos em uma loja num determinado dia.
{35, 33, 36, 35, 37, 36, 39, 40, 42, 43, 35, 36, 42}
Nesse caso, existem dois números de sapatos que aparecem mais vezes: 35 e 36. Logo, a moda pode ser:
Mo = 35 ou Mo = 36
Quando isso ocorre, dizemos que o conjunto de dados é bimodal.
Definição de Mediana (Md): é o valor (pertencente ou não ao conjunto de dados) que divide o conjunto de dados em dois subconjuntos de mesmo tamanho. De uma forma mais simples, é o valor que divide o conjunto de dados ao meio.
Para determinar a mediana de um conjunto de dados é necessário, primeiro, construir o rol. O rol é a ordenação do conjunto de dados em ordem crescente ou decrescente.
1. Mediana de um conjunto de dados com número de elementos ímpar.
Considere o conjunto de dados abaixo, referentes ao salário médio dos funcionários de uma empresa em reais.
Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980
Observe que nesse conjunto de dados temos 9 elementos, 9 salários. Primeiro devemos montar o rol:
Rol = {1100, 1200, 1210, 1250, 1300, 1450, 1500, 1600, 1980}
Quando o número de elementos do conjunto de dados for ímpar, a mediana é o valor que divide o conjunto ao meio, portanto Md = 1300. Observe que à esquerda e à direita de 1300 existem 4 elementos.
2. Mediana de um conjunto de dados com número de elementos ímpar.
Considere o conjunto de dados abaixo, referente ao salário médio dos funcionários de uma empresa.
Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980 1420
Rol = { 1100, 1200, 1210, 1250, 1300, 1420, 1450, 1500, 1600, 1980}
Nesse conjunto existem 10 elementos. Nesse caso a mediana será a média aritmética dos dois valores centrais. Note que tanto à direita como à esquerda dos dois valores centrais há 4 elementos. Assim,
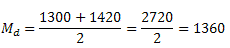
Mo = 7.
Exemplo 3. Os dados abaixo são referentes ao número dos calçados vendidos em uma loja num determinado dia.
{35, 33, 36, 35, 37, 36, 39, 40, 42, 43, 35, 36, 42}
Nesse caso, existem dois números de sapatos que aparecem mais vezes: 35 e 36. Logo, a moda pode ser:
Mo = 35 ou Mo = 36
Quando isso ocorre, dizemos que o conjunto de dados é bimodal.
Definição de Mediana (Md): é o valor (pertencente ou não ao conjunto de dados) que divide o conjunto de dados em dois subconjuntos de mesmo tamanho. De uma forma mais simples, é o valor que divide o conjunto de dados ao meio.
Para determinar a mediana de um conjunto de dados é necessário, primeiro, construir o rol. O rol é a ordenação do conjunto de dados em ordem crescente ou decrescente.
1. Mediana de um conjunto de dados com número de elementos ímpar.
Considere o conjunto de dados abaixo, referentes ao salário médio dos funcionários de uma empresa em reais.
Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980
Observe que nesse conjunto de dados temos 9 elementos, 9 salários. Primeiro devemos montar o rol:
Rol = {1100, 1200, 1210, 1250, 1300, 1450, 1500, 1600, 1980}
Quando o número de elementos do conjunto de dados for ímpar, a mediana é o valor que divide o conjunto ao meio, portanto Md = 1300. Observe que à esquerda e à direita de 1300 existem 4 elementos.
2. Mediana de um conjunto de dados com número de elementos ímpar.
Considere o conjunto de dados abaixo, referente ao salário médio dos funcionários de uma empresa.
Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980 1420
Rol = { 1100, 1200, 1210, 1250, 1300, 1420, 1450, 1500, 1600, 1980}
Nesse conjunto existem 10 elementos. Nesse caso a mediana será a média aritmética dos dois valores centrais. Note que tanto à direita como à esquerda dos dois valores centrais há 4 elementos. Assim,
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Especialista em Estatística e Modelagem Matemática
Teorema de Pitágoras
professor Antonio Carlos Carneiro Barroso
http://ensinodematemtica.blogspot.com
http://accbarrosogestar.blogspot.com.br
extraido de www.colegioweb.com.br
(c. 582-c. 500 a.C.), filósofo e matemático grego. Suas doutrinas influenciaram Platão. Até o ano 530 a.C., Pitágoras viveu em Crotona, uma colônia grega ao sul da Itália, onde fundou um movimento com propósitos religiosos, políticos e filosóficos, conhecido como pitagorismo. Sua filosofia só é conhecida através da obra de seus discípulos.
Os pitagóricos aconselhavam obediência, silêncio, abstinência de alimentos, simplicidade no vestir e nas posses e o hábito da auto-análise. Acreditavam na imortalidade e na transmigração da alma.
Entre as amplas investigações matemáticas realizadas pelos pitagóricos destacam-se os estudos dos números pares e ímpares, dos números primos e dos quadrados. Através destes estudos, foi estabelecido uma base científica para a matemática. Em geometria, a grande descoberta da escola foi o teorema da hipotenusa, conhecido como teorema de Pitágoras. A astronomia dos pitagóricos marcou um importante avanço no pensamento científico clássico já que foram eles os primeiros a considerar a Terra como um globo que gira, junto a outros planetas, em torno de um fogo central.
Pitágoras
Teorema que estabelece que o quadrado da hipotenusa de um triângulo retângulo é igual à soma dos quadrados dos outros dois lados, chamados de catetos.
O teorema de Pitágoras é um assunto sempre cobrado nas provas dp vestibular. O desafio sugerido pode ser resolvido destacando vários triângulos e somando as diversas hipotenusas encontradas.
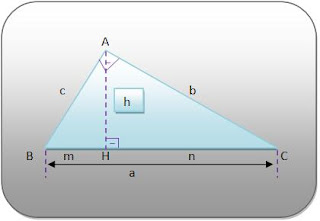
Aplique a seguinte propriedade:
"Em todo triângulo retângulo e isóceles, a hipotenusa é igualao produto de um dos catetos por 2".
Assim: m2 = a2+a2
m2 = 2a2
m = a 2
m = a 2

http://ensinodematemtica.blogspot.com
http://accbarrosogestar.blogspot.com.br
extraido de www.colegioweb.com.br
(c. 582-c. 500 a.C.), filósofo e matemático grego. Suas doutrinas influenciaram Platão. Até o ano 530 a.C., Pitágoras viveu em Crotona, uma colônia grega ao sul da Itália, onde fundou um movimento com propósitos religiosos, políticos e filosóficos, conhecido como pitagorismo. Sua filosofia só é conhecida através da obra de seus discípulos.
Os pitagóricos aconselhavam obediência, silêncio, abstinência de alimentos, simplicidade no vestir e nas posses e o hábito da auto-análise. Acreditavam na imortalidade e na transmigração da alma.
Entre as amplas investigações matemáticas realizadas pelos pitagóricos destacam-se os estudos dos números pares e ímpares, dos números primos e dos quadrados. Através destes estudos, foi estabelecido uma base científica para a matemática. Em geometria, a grande descoberta da escola foi o teorema da hipotenusa, conhecido como teorema de Pitágoras. A astronomia dos pitagóricos marcou um importante avanço no pensamento científico clássico já que foram eles os primeiros a considerar a Terra como um globo que gira, junto a outros planetas, em torno de um fogo central.
Pitágoras
Teorema que estabelece que o quadrado da hipotenusa de um triângulo retângulo é igual à soma dos quadrados dos outros dois lados, chamados de catetos.
O teorema de Pitágoras é um assunto sempre cobrado nas provas dp vestibular. O desafio sugerido pode ser resolvido destacando vários triângulos e somando as diversas hipotenusas encontradas.
Aplique a seguinte propriedade:
"Em todo triângulo retângulo e isóceles, a hipotenusa é igualao produto de um dos catetos por 2".
Assim: m2 = a2+a2
m2 = 2a2
m = a 2
m = a 2

Dia da Consciência Negra e o herói chamado Zumbi

Zumbi líder do quilombo dos Palmares
Zumbi foi o grande líder do quilombo dos Palmares, respeitado herói da resistência antiescravagista. Pesquisas e estudos indicam que nasceu em 1655, sendo descendente de guerreiros angolanos. Em um dos povoados do quilombo, foi capturado quando garoto por soldados e entregue ao padre Antonio Melo, de Porto Calvo. Criado e educado por este padre, o futuro líder do Quilombo dos Palmares já tinha apreciável noção de Português e Latim aos 12 anos de idade, sendo batizado com o nome de Francisco. Padre Antônio Melo escreveu várias cartas a um amigo, exaltando a inteligência de Zumbi (Francisco). Em 1670, com quinze anos, Zumbi fugiu e voltou para o Quilombo. Tornou-se um dos líderes mais famosos de Palmares. "Zumbi" significa: a força do espírito presente. Baluarte da luta negra contra a escravidão, Zumbi foi o último chefe do Quilombo dos Palmares.
O nome Palmares foi dado pelos portugueses, em razão do grande número de palmeiras encontradas na região da Serra da Barriga, ao sul da capitania de Pernambuco, hoje, estado de Alagoas. Os que lá viviam chamavam o quilombo de Angola Janga (Angola Pequena). Palmares constituiu-se como abrigo não só de negros, mas também de brancos pobres, índios e mestiços extorquidos pelo colonizador. Os quilombos, que na língua banto significam "povoação", funcionavam como núcleos habitacionais e comerciais, além de local de resistência à escravidão, já que abrigavam escravos fugidos de fazendas. No Brasil, o mais famoso deles foi Palmares.
O Quilombo dos Palmares existiu por um período de quase cem anos, entre 1600 e 1695. No Quilombo de Palmares (o maior em extensão), viviam cerca de vinte mil habitantes. Nos engenhos e senzalas, Palmares era parecido com a Terra Prometida, e Zumbi, era tido como eterno e imortal, e era reconhecido como um protetor leal e corajoso. Zumbi era um extraordinário e talentoso dirigente militar. Explorava com inteligência as peculiaridades da região. No Quilombo de Palmares plantavam-se frutas, milho, mandioca, feijão, cana, legumes, batatas. Em meados do século XVII, calculavam-se cerca de onze povoados. A capital era Macaco, na Serra da Barriga.
A Domingos Jorge Velho, um bandeirante paulista, vulto de triste lembrança da história do Brasil, foi atribuído a tarefa de destruir Palmares. Para o domínio colonial, aniquilar Palmares era mais que um imperativo atribuído, era uma questão de honra. Em 1694, com uma legião de 9.000 homens, armados com canhões, Domingos Jorge Velho começou a empreitada que levaria à derrota de Macaco, principal povoado de Palmares. Segundo Paiva de Oliveira, Zumbi foi localizado no dia 20 de novembro de 1695, vítima da traição de Antônio Soares. “O corpo perfurado por balas e punhaladas foi levado a Porto Calvo. A sua cabeça foi decepada e remetida para Recife onde, foi coberta por sal fino e espetada em um poste até ser consumida pelo tempo”.
O Quilombo dos Palmares foi defendido no século XVII durante anos por Zumbi contra as expedições militares que pretendiam trazer os negros fugidos novamente para a escravidão. O Dia da Consciência Negra é celebrado em 20 de novembro no Brasil e é dedicado à reflexão sobre a inserção do negro na sociedade brasileira. A data foi escolhida por coincidir com o dia da morte de Zumbi dos Palmares, em 1695.
A lei 10.639, de 9 de janeiro de 2003, incluiu o dia 20 de novembro no calendário escolar, data em que comemoramos o Dia Nacional da Consciência Negra. A mesma lei também tornou obrigatório o ensino sobre História e Cultura Afro-Brasileira. Nas escolas as aulas sobre os temas: História da África e dos africanos, luta dos negros no Brasil, cultura negra brasileira e o negro na formação da sociedade nacional, propiciarão o resgate das contribuições dos povos negros nas áreas social, econômica e política ao longo da história do país.
Amélia Hamze Profª da FEB/CETEC
Equações Biquadradas
Equações Biquadradas
1.0 - Definição. Forma geral da equação.
Define-se equação biquadrada como a equação incompleta do quarto grau, que, após efetuadas todas as reduções possíveis, contém
apenas termos onde a incógnita está submetida a expoentes de grau par.
E desse modo, podemos escrever a forma geral da equação biquadrada como:














http://www.matematicamuitofacil.com/
1.0 - Definição. Forma geral da equação.
Define-se equação biquadrada como a equação incompleta do quarto grau, que, após efetuadas todas as reduções possíveis, contém
apenas termos onde a incógnita está submetida a expoentes de grau par.
E desse modo, podemos escrever a forma geral da equação biquadrada como:














http://www.matematicamuitofacil.com/
NÚMEROS INTEIROS RELATIVOS
INTRODUÇÃO:
Observe que, no conjunto dos números naturais, a operação de subtração nem sempre é possivel
exemplos:
a) 5 - 3 = 2 (possível: 2 é um número natural)
b) 9 - 9 = 0 ( possível: 0 é um número natural)
c) 3 - 5 = ? ( impossível nos números naturais)
Para tonar sempre possível a subtração, foi criado o conjunto dos números inteiros relativos,
-1, -2, -3,.........
lê-se: menos um ou 1 negativo
lê-se: menos dois ou dois negativo
lê-se: menos três ou três negativo
Reunindo os números negativos, o zero e os números positivos, formamos o conjunto dos numeros inteiros relativos, que será representado por Z.
Z = { .....-3, -2, -1, 0, +1, +2, +3,......}
Importante: os números inteiros positivos podem ser indicados sem o sinal de +.
exemplo
a) +7 = 7
b) +2 = 2
c) +13 = 13
d) +45 = 45
Sendo que o zero não é positivo nem negativo
EXERCICIOS
1) Observe os números e diga:
-15, +6, -1, 0, +54, +12, -93, -8, +23, -72, +72
a) Quais os números inteiros negativos?
R: -15,-1,-93,-8,-72
b) Quais são os números inteiros positivos?
R: +6,+54,+12,+23,+72
2) Qual o número inteiro que não é nem positivo nem negativo?
R: É o zero
3) Escreva a leitura dos seguintes números inteiros:
a) -8 =(R: oito negativo)
b)+6 = (R: seis positivo)
c) -10 = (R: dez negativo)
d) +12 = (R: doze positivo)
e) +75 = (R: setenta e cinco positivo)
f) -100 = (R: cem negativo)
4) Quais das seguintes sentenças são verdadeiras?
a) +4 = 4 = ( V)
b) -6 = 6 = ( F)
c) -8 = 8 = ( F)
d) 54 = +54 = ( V)
e) 93 = -93 = ( F )
5) As temperaturas acima de 0°C (zero grau) são representadas por números positivos e as temperaturas abaixo de 0°C, por números negativos. Represente a seguinte situação com números inteiros relativos:
a) 5° acima de zero = (R: +5)
b) 3° abaixo de zero = (R: -3)
c) 9°C abaixo de zero= (R: -9)
d) 15° acima de zero = ( +15)
REPRESENTAÇÃO DOS NÚMEROS INTEIROS NA RETA
Vamos traçar uma reta e marcar o ponto 0. À direta do ponto 0, com uma certa unidade de medida, assinalemos os pontos que correspondem aos números positivos e à esquerda de 0, com a mesma unidade, assinalaremos os pontos que correspondem aos números negativos.
_I___I___I___I___I___I___I___I___I___I___I___I___I___I_
-6.. -5...-4. -3,. -2,..-1,.. 0,.+1,.+2,.+3,.+4,..+5,.+6
exercícios
1) Escreva os números inteiros:
a) compreendidos entre 1 e 7 (R: 2,3,4,5,6)
b) compreendidos entre -3 e 3 (R: -2,-1,0,1,2)
c) compreendidos entre -4 e 2 ( R: -3, -2, -1, 0, 1)
d) compreendidos entre -2 e 4 (R: -1, 0, 1, 2, 3 )
e) compreendidos entre -5 e -1 ( R: -4, -3, -2)
f) compreendidos entre -6 e 0 (R: -5, -4, -3, -2, -1)
2) Responda:
a) Qual é o sucessor de +8? (R: +9)
b) Qual é o sucessor de -6? (R: -5)
c) Qual é o sucessor de 0 ? (R: +1)
d) Qual é o antecessor de +8? (R: +7)
e) Qual é o antecessor de -6? ( R: -7)
f) Qual é o antecessor de 0 ? ( R: -1)
3) Escreva em Z o antecessor e o sucessor dos números:
a) +4 (R: +3 e +5)
b) -4 (R: -5 e - 3)
c) 54 (R: 53 e 55 )
d) -68 (R: -69 e -67)
e) -799 ( R: -800 e -798)
f) +1000 (R: +999 e + 1001)
NÚMEROS OPOSTOS E SIMÉTRICOS
Na reta numerada, os números opostos estão a uma mesma distancia do zero.
-I___I___I___I___I___I___I___I___I___I___I___I___I___I_
-6.. -5...-4. -3,. -2,..-1,.. 0,.+1,.+2,.+3,.+4,..+5,.+6
Observe que cada número inteiro, positivo ou negativo, tem um correspondente com sinais deferentes
exemplo
a) O oposto de +1 é -1.
b) O oposto de -3 é +3.
c) O oposto de +9 é -9.
d) O oposto de -5 é +5.
Obsevação: O oposto de zero é o próprio zero.
EXERCÍCIOS
1) Determine:
a) O oposto de +5 = (R:-5)
b) O oposto de -9 = (R: +9)
c) O oposto de +6 = (R: -6)
d) O oposto de -6 = (R: +6)
e) O oposto de +18 = (R: -18)
f) O oposto de -15 = (R: +15)
g) O oposto de +234= (R: -234)
h) O oposto de -1000 = (R: +1000)
COMPARAÇÃO DE NÚMEROS INTEIROS ,
Observe a representação gráfica dos números inteiros na reta.
-I___I___I___I___I___I___I___I___I___I___I___I___I___I_
-6.. -5...-4. -3,. -2,..-1,.. 0,.+1,.+2,.+3,.+4,..+5,.+6
Dados dois números quaisquer, o que está à direita é o mair deles, e o que está à esquerda, o menor deles.
exemplos
a) -1 maior; -4, poque -1 está à direita de -4.
b) +2 maior; -4, poque +2 está a direita de -4
c) -4 menor -2 , poque -4 está à esquerda de -2.
d) -2 menor +1, poque -2 está à esquerda de +1.
exercicios
1) Qual é o número maior ?
a) +1 ou -10 (R:+1)
b) +30 ou 0 (R: +30)
c) -20 ou 0 ( R: 0)
d) +10 ou -10 (R: +10)
e) -20 ou -10 (R: -10)
f) +20 ou -30 (R: +20)
g) -50 ou +50 (R:+50)
h) -30 ou -15 (R:-15)
2) compare os seguites pares de números, dizendo se o primeiro é maior, menor ou igual
a) +2 e + 3 (menor)
b) +5 e -5 (maior)
c) -3 e +4 (nenor)
d) +1 e -1 (maior)
e) -3 e -6 ( maior)
f) -3 e -2 (menor)
g) -8 e -2 (menor)
h) 0 e -5 (maior)
i) -2 e 0 (nenor)
j) -2 e -4 (maior)
l) -4 e -3 (menor)
m) 5 e -5 (maior)
n) 40 e +40 ( igual)
o) -30 e -10 (menor)
p) -85 e 85 (menor)
q) 100 e -200 (maior)
r) -450 e 300 (menor)
s) -500 e 400 (menor)
3) coloque os números em ordem crescente.
a) -9,-3,-7,+1,0 (R: -9,-7,-3,0,1)
b) -2, -6, -5, -3, -8 (R: -8, -6,-5, -3,-2)
c) 5,-3,1,0,-1,20 (R: -3,-1,0,1,5,20)
d) 25,-3,-18,+15,+8,-9 (R: -18,-9,-3,+8,+15,+25)
e) +60,-21,-34,-105,-90 ( R: -105,-90,-34,-21, +60)
f) -400,+620,-840,+1000,-100 ( R: -840,-400,-100,+620,+1000)
4) Coloque os números em ordem decrescente
a) +3,-1,-6,+5,0 (R: +5,+3,0,-1,-6)
b) -4,0,+4,+6,-2 ( R: +6,+4,0,-2,-4)
c) -5,1,-3,4,8 ( R: 8,4,1,-3,-5)
d) +10,+6,-3,-4,-9,+1 (R: +10,+6,+1,-3,-4,-9)
e) -18,+83,0,-172, -64 (R: +83,0,-18,-64,-172)
f) -286,-740, +827,0,+904 (R: +904,+827,0,-286,-740)
ADIÇÃO E SUBTRAÇÃO COM NÚMEROS INTEIROSADIÇÃO1) Adição de números positivos
A soma de dois números positivos é um número positivo.
EXEMPLO
a) (+2) + (+5) = +7
b) (+1) + (+4) = +5
c) (+6) + (+3) = +9
Simplificando a maneira de escrever
a) +2 +5 = +7
b) +1 + 4 = +5
c) +6 + 3 = +9
Observe que escrevemos a soma dos números inteiros sem colocar o sinal + da adição e eliminamos os parêteses das parcelas.
2) Adição de números negativos
A soma de dois numeros negativos é um número negativo
Exemplo
a) (-2) + (-3) = -5
b) (-1) + (-1) = -2
c) (-7) + (-2) = -9
Simplificando a maneira de escrever
a) -2 - 3 = -5
b) -1 -1 = -2
c) -7 - 2 = -9
Observe que podemos simplificar a maneira de escrever deixando de colocar o sinal de + na operação e eliminando os parênteses das parcelas.
EXERCÍCIOS
1) Calcule
a) +5 + 3 = (R:+8)
b) +1 + 4 = (R: +5)
c) -4 - 2 = (R: -6)
d) -3 - 1 = (R: -4)
e) +6 + 9 = (R: +15)
f) +10 + 7 = (R: +17)
g) -8 -12 = (R: -20)
h) -4 -15 = (R: -19)
i) -10 - 15 = (R: -25)
j) +5 +18 = (R: +23)
l) -31 - 18 = (R: -49)
m) +20 +40 = (R: + 60)
n) -60 - 30 = (R: -90)
o) +75 +15 = (R: +90)
p) -50 -50 = (R: -100)
2) Calcule:
a) (+3) + (+2) = (R: +5)
b) (+5) + (+1) = (R: +6)
c) (+7) + ( +5) = (R: +12)
d) (+2) + (+8) = (R: +10)
e) (+9) + (+4) = (R: +13)
f) (+6) + (+5) = (R: +11)
g) (-3) + (-2) = (R: -5)
h) (-5) + (-1) = (R: -6)
i) (-7) + (-5) = (R: -12)
j) (-4) + (-7) = (R: -11)
l) (-8) + ( -6) = (R: -14)
m) (-5) + ( -6) = (R: -11)
3) Calcule:
a) ( -22) + ( -19) = (R: -41)
b) (+32) + ( +14) = (R: +46)
c) (-25) + (-25) = (R: -50)
d) (-94) + (-18) = (R: -112)
e) (+105) + (+105) = (R: +210)
f) (-280) + (-509) = (R: -789)
g) (-321) + (-30) = (R: -350)
h) (+200) + (+137) = (R: +337)
3) Adição de números com sinais diferentes
A soma de dois números inteiros de sinais diferentes é obtida subtraindo-se os valores absolutos, dando-se o sinal do número que tiver maior valor absoluto.
exemplos
a) (+6) + ( -1) = +5
b) (+2) + (-5) = -3
c) (-10) + ( +3) = -7
simplificando a maneira de escrever
a) +6 - 1 = +5
b) +2 - 5 = -3
c) -10 + 3 = -7
Note que o resultado da adição tem o mesmo sinal que o número de maior valor absoluto
Observação:
Quando as parcelas são números opostos, a soma é igual a zero.
Exemplo
a) (+3) + (-3) = 0
b) (-8) + (+8) = 0
c) (+1) + (-1) = 0
simplificando a maneira de escrever
a) +3 - 3 = 0
b) -8 + 8 = 0
c) +1 - 1 = 0
4) Um dos numeros dados é zero
Quando um dos números é zero , a soma é igual ao outro número.
exemplo
a) (+5) +0 = +5
b) 0 + (-3) = -3
c) (-7) + 0 = -7
Simplificando a maneira de escrever
a) +5 + 0 = +5
b) 0 - 3 = -3
c) -7 + 0 = -7
exercícios
1) Calcule:
a) +1 - 6 = -5
b) -9 + 4 = -5
c) -3 + 6 = +3
d) -8 + 3 = -5
e) -9 + 11 = +2
f) +15 - 6 = +9
g) -2 + 14 = +12
h) +13 -1 = +12
i) +23 -17 = +6
j) -14 + 21 = +7
l) +28 -11 = +17
m) -31 + 30 = -1
2) Calcule:
a) (+9) + (-5) = +4
b) (+3) + (-4) = -1
c) (-8) + (+6) = -2
d) (+5) + (-9) = -4
e) (-6) + (+2) = -4
f) (+9) + (-1) = +8
g) (+8) + (-3) = +5
h) (+12) + (-3) = +9
i) (-7) + (+15) = +8
j) (-18) + (+8) = -10
i) (+7) + (-7) = 0
l) (-6) + 0 = -6
m) +3 + (-5) = -2
n) (+2) + (-2) = 0
o) (-4) +10 = +6
p) -7 + (+9) = +2
q) +4 + (-12) = -8
r) +6 + (-4) = +2
PROPRIEDADE DA ADIÇÃO
1) Fechamento : a soma de dois números inteiros é sempre um número inteiro
exemplo (-4) + (+7) =( +3)
2) Comutativa: a ordem das parcelas não altera a soma.
exemplo: (+5) + (-3) = (-3) + (+5)
3) Elemento neutro: o número zero é o elemento neutro da adição.
exemplo: (+8) + 0 = 0 + (+8) = +8
4) Associativa: na adição de três números inteiros, podemos associar os dois primeiros ou os dois últimos, sem que isso altere o resultado.
exemplo: [(+8) + (-3) ] + (+4) = (+8) + [(-3) + (+4)]
5) Elemento oposto: qualquer número inteiro admite um simétrico ou oposto.
exemplo: (+7) + (-7) = 0
ADIÇÃO DE TRÊS OU MAIS NÚMEROS
Para obter a soma de três ou mais números adicionamos os dois primeiros e, em seguida, adicionamos esse resultado com o terceiro, e assim por diante.
exemplos
1) -12 + 8 - 9 + 2 - 6 =
= -4 - 9 + 2 - 6 =
= -13 + 2 - 6 =
= -11 - 6 =
= -17
2) +15 -5 -3 +1 - 2 =
= +10 -3 + 1 - 2 =
= +7 +1 -2 =
= +8 -2 =
= +6
Na adição de números inteiros podemos cancelar números opostos, poque a soma deles é zero.
INDICAÇÃO SIMPLIFICADA
a) podemos dispensar o sinal de + da primeira parcela quando esta for positiva.
exemplos
a) (+7) + (-5) = 7 - 5 = +2
b) (+6) + (-9) = 6 - 9 = -3
b) Podemos dispensar o sinal + da soma quando esta for positiva
exemplos
a) (-5) + (+7) = -5 + 7 = 2
b) (+9) + (-4) = 9 - 4 = 5
EXERCÍCIOS
1) Calcule
a) 4 + 10 + 8 = (R: 22)
b) 5 - 9 + 1 = (R: -3)
c) -8 - 2 + 3 = (R: -7)
d) -15 + 8 - 7 = (R: -14)
e) 24 + 6 - 12 = (R:+18)
f) -14 - 3 - 6 - 1 = (R: -24)
g) -4 + 5 + 6 + 3 - 9 = (R: + 1)
h) -1 + 2 - 4 - 6 - 3 - 8 = (R: -20)
i) 6 - 8 - 3 - 7 - 5 - 1 + 0 - 2 = (R: -20)
j) 2 - 10 - 6 + 14 - 1 + 20 = (R: +19)
l) -13 - 1 - 2 - 8 + 4 - 6 - 10 = (R: -36)
2) Efetue, cancelando os números opostos:
a) 6 + 4 - 6 + 9 - 9 = (R: +4)
b) -7 + 5 - 8 + 7 - 5 = (R: -8)
c) -3 + 5 + 3 - 2 + 2 + 1 = (R: +6)
d) -6 + 10 + 1 - 4 + 6= (R: +7)
e) 10 - 6 + 3 - 3 - 10 - 1 = (R: -7)
f) 15 - 8 + 4 - 4 + 8 - 15 = (R: 0)
3) Coloque em forma simplificada ( sem parênteses)
a) (+1) + (+4) +(+2) = (R: 1 +4 + 2)
b) (+1) + (+8) + (-2) = (R: 1 + 8 - 2)
c) (+5) +(-8) + (-1) = (R: +5 - 8 - 1)
d) (-6) + (-2) + (+1) = (R: -6 - 2 + 1)
4) Calcule:
a) (-2) + (-3) + (+2) = (R: -3)
b) (+3) + (-3) + (-5) = (R: -5)
c) (+1) + (+8) +(-2) = (R: +7 )
d) (+5) + (-8) + (-1) = (R: -4)
e) (-6) + (-2) + (+1) = (R: -7)
f) (-8) + ( +6) + (-2) = (R: -4)
g) (-7) + 6 + (-7) = (R: -8)
h) 6 + (-6) + (-7) = (R: -7)
i) -6 + (+9) + (-4) = (R: -1)
j) (-4) +2 +4 + (+1) = (R: +3)
5) Determine as seguintes somas
a) (-8) + (+10) + (+7) + (-2) = (R: +7)
b) (+20) + (-19) + (-13) + (-8) = (R: -20)
c) (-5) + (+8) + (+2) + (+9) = (R: +14)
d) (-1) + (+6) + (-3) + (-4) + (-5) = (R: -7)
e) (+10) + (-20) + (-15) + (+12) + (+30) + (-40) = (R: -23)
f) (+3) + (-6) + (+8) = (R: +5)
g) (-5) + (-12) + (+3) = (R: -14)
h) (-70) + (+20) + (+50) = (R: 0)
i) (+12) + (-25) + (+15) = (R: +2)
j) (-32) + (-13) + (+21) = (R: -24)
l) (+7) + (-5) + (-3) + (+10) = (R: +9)
m) (+12) + (-50) + (-8) + (+13) = (R: -33)
n) (-8)+(+4)+ (+8) + (-5) + (+3) = (R: +2)
o) (-36) + (-51) + (+100) + (-52) = (R: -39)
p) (+17) + (+13) + (+20) + (-5) + (-45) = (R:0)
6) Dados os números x= 6, y = 5 e z= -6, calcule
a) x + y = (R: +11)
b) y + z = (R: -4)
c) x + z = (R: -3)
SUBTRAÇÃO
A operação de subtração é uma operação inversa à da adição
Exemplos
a) (+8) - (+4) = (+8) + (-4) = = +4
b) (-6) - (+9) = (-6) + (-9) = -15
c) (+5) - (-2) = ( +5) + (+2) = +7
Conclusão: Para subtraimos dois números relativos, basta que adicionemos ao primeiro o oposto do segundo.
Observação: A subtração no conjunto Z tem apenas a propriedade do fechamento ( a subtração é sempre possivel)
ELIMINAÇÃO DE PARÊNTESES PRECEDIDOS DE SINAL NEGATIVO
Para facilitar o cálculo, eliminamos os parênteses usando o segnificado do oposto
veja:
a) -(+8) = -8 (significa o oposto de +8 é -8 )
b) -(-3) = +3 (significa o oposto de -3 é +3)
analogicamente:
a) -(+8) - (-3) = -8 +3 = -5
b) -(+2) - (+4) = -2 - 4 = -6
c) (+10) - (-3) - +3) = 10 + 3 - 3 = 10
conclusão: podemos eliminar parênteses precedidos de sinal negativo trocando-se o sínal do número que está dentro dos parênteses.
EXERCÍCIOS
1) Elimine os parênteses
a) -(+5) = -5
b) -(-2) = +2
c) - (+4) = -4
d) -(-7) = +7
e) -(+12) = -12
f) -(-15) = +15
g) -(-42) = +42
h) -(+56) = -56
2) Calcule:
a) (+7) - (+3) = (R: +4)
b) (+5) - (-2) = (R: +7)
c) (-3) - ( +8) = (R: -11)
d) (-1) -(-4) = (R: +3)
e) (+3) - (+8) = (R: -5)
f) (+9) - (+9) = (R: 0 )
g) (-8) - ( +5) = (R: -13)
h) (+5) - (-6) = (R: +11)
i) (-2) - (-4) = (R: +2)
j) (-7) - (-8) = (R: +1)
l) (+4) -(+4) = (R: 0)
m) (-3) - ( +2) = (R: -5)
n) -7 + 6 = (R: -1)
o) -8 -7 = (R: -15)
p) 10 -2 = (R: 8)
q) 7 -13 = (R: -6)
r) -1 -0 = (R: -1)
s) 16 - 20 = (R: -4)
t) -18 -9 = (R: -27)
u) 5 - 45 = (R:-40)
v) -15 -7 = (R: -22)
x) -8 +12 = (R: 4)
z) -32 -18 = (R:-50)
3) Calcule:
a) 7 - (-2) = (R: 9)
b) 7 - (+2) = (R: 5)
c) 2 - (-9) = (R: 11)
d) -5 - (-1) = (R: -4)
e) -5 -(+1) = (R: -6)
f) -4 - (+3) = (R: -7)
g) 8 - (-5) = (R: 13)
h) 7 - (+4) = (R: 3)
i) 26 - 45 = (R: -19)
j) -72 -72 = (R: -144)
l) -84 + 84 = (R: 0)
m) -10 -100 = (R: -110)
n) -2 -4 -1 = (R: -7)
o) -8 +6 -1 = (R: -3)
p) 12-7 + 3 = (R: 8)
q) 4 + 13 - 21 = (R: -4)
r) -8 +8 + 1 = (R: 1)
s) -7 + 6 + 9 = (R: 8)
t) -5 -3 -4 - 1 = (R: -13)
u) +10 - 43 -17 = (R: -50)
v) -6 -6 + 73 = (R: 61)
x) -30 +30 - 40 = (R: -40)
z) -60 - 18 +50 = (R: -28)
4) Calcule:
a) (-4) -(-2)+(-6) = (R: -8)
b) (-7)-(-5)+(-8) = (R: -10)
c) (+7)-(-6)-(-8) = (R: 21)
d) (-8) + (-6) -(+3) = (R: -17)
e) (-4) + (-3) - (+6) = (R: -13)
f) 20 - (-6) - (-8) = (R: 34)
g) 5 - 6 - (+7) + 1 = (R: -7)
h) -10 - (-3) - (-4) = (R: -3)
i) (+5) + (-8) = (R: -3)
j) (-2) - (-3) = (R: +1)
l) (-3) -(-9) = (R: +6)
m) (-7) - (-8) =(R: +1)
n) (-8) + (-6) - (-7) = (R: -7)
o) (-4) + (-6) + (-3) = (R: -13)
p) 15 -(-3) - (-1) = (R: +19)
q) 32 - (+1) -(-5) = (R: +36)
r) (+8) - (+2) = (R:+6)
s) (+15) - (-3) = (R: +18)
t) (-18) - (-10) = (R: -8)
u) (-25) - (+22) = (R:-47)
v) (-30) - 0 = (R: -30)
x) (+180) - (+182) = (R: -2)
z) (+42) - (-42) = (R: +84)
5) Calcule:
a) (-5) + (+2) - (-1) + (-7) = (R: -9)
b) (+2) - (-3) + (-5) -(-9) = (R: 9)
c) (-2) + (-1) -(-7) + (-4) = (R: 0)
d) (-5) + (-6) -(-2) + (-3) = (R: -12)
e) (+9) -(-2) + (-1) - (-3) = (R: 13)
f) 9 - (-7) -11 = (R: 5 )
g) -2 + (-1) -6 = (R: -9)
h) -(+7) -4 -12 = (R: -23)
i) 15 -(+9) -(-2) = (R: 8 )
j) -25 - ( -5) -30 = (R: -50)
l) -50 - (+7) -43 = (R: -100)
m) 10 -2 -5 -(+2) - (-3) = (R: 4)
n) 18 - (-3) - 13 -1 -(-4) = (R: 11)
o) 5 -(-5) + 3 - (-3) + 0 - 6 = (R: 10)
p) -28 + 7 + (-12) + (-1) -4 -2 = (R: -40)
q) -21 -7 -6 -(-15) -2 -(-10) = (R: -11)
r) 10 -(-8) + (-9) -(-12)-6 + 5 = (R: 20)
s) (-75) - (-25) = (R: -50)
t) (-75) - (+25) = (R: -100)
u) (+18) - 0 = (R: +18)
v) (-52) - (-52) = (R:0)
x) (-16)-(-25) = (R:+9)
z) (-100) - (-200) = (R:+100)
ELIMINAÇÃO DOS PARENTESES
1) parenteses precedidos pelo sinal +
Ao eliminarmos os parênteses e o sinal + que os precede, devemos conservar os sinais dos números contidos nesses parênteses.
exemplo
a) + (-4 + 5) = -4 + 5
b) +(3 +2 -7) = 3 +2 -7
2) Parênteses precedidos pelo sinal -
Ao eliminarmos os parênteses e o sinal de - que os precede, devemos trocar os sinais dos números contidos nesses parênteses.
exemplo
a) -(4 - 5 + 3) = -4 + 5 -3
b) -(-6 + 8 - 1) = +6 -8 +1
EXERCICIOS
1) Elimine os parênteses:
a) +(-3 +8) = (R: -3 + 8)
b) -(-3 + 8) = (R: +3 - 8)
c) +(5 - 6) = (R: 5 -6 )
d) -(-3-1) = (R: +3 +1)
e) -(-6 + 4 - 1) = (R: +6 - 4 + 1)
f) +(-3 -2 -1) = (R: -3 -2 -1 )
g) -(4 -6 +8) = (R: -4 +6 +8)
h) + (2 + 5 - 1) = (R: +2 +5 -1)
2) Elimine os parênteses e calcule:
a) + 5 + ( 7 - 3) = (R: 9)
b) 8 - (-2-1) = (R: 11)
c) -6 - (-3 +2) = (R: -5)
d) 18 - ( -5 -2 -3 ) = (R: 28)
e) 30 - (6 - 1 +7) = (R: 18)
f) 4 + (-5 + 0 + 8 -4) = (R: 3)
g) 4 + (3 - 5) + ( -2 -6) = (R: -6)
h) 8 -(3 + 5 -20) + ( 3 -10) = (R: 13)
i) 20 - (-6 +8) - (-1 + 3) = (R: 16)
j) 35 -(4-1) - (-2 + 7) = (R: 27)
3) Calcule:
a) 10 - ( 15 + 25) = (R: -30)
b) 1 - (25 -18) = (R: -6)
c) 40 -18 - ( 10 +12) = (R: 0)
d) (2 - 7) - (8 -13) = (R: 0 )
e) 7 - ( 3 + 2 + 1) - 6 = (R: -5)
f) -15 - ( 3 + 25) + 4 = (R: -39)
g) -32 -1 - ( -12 + 14) = (R: -35)
h) 7 + (-5-6) - (-9 + 3) = (R: 2)
i) -(+4-6) + (2 - 3) = (R: 1)
j) -6 - (2 -7 + 1 - 5) + 1 = (R: 4)
EXPRESSÕES COM NÚMEROS INTEIROS RELATIVOS
Lembre-se de que os sinais de associação são eliminados obedecendo à seguinte ordem:
1°) PARÊNTESES ( ) ;
2°) COLCHETES [ ] ;
3°) CHAVES { } .
Exemplos:
1°) exemplo
8 + ( +7 -1 ) - ( -3 + 1 - 5 ) =
8 + 7 - 1 + 3 - 1 + 5 =
23 - 2 = 21
2°) exemplo
10 + [ -3 + 1 - ( -2 + 6 ) ] =
10 + [ -3 + 1 + 2 - 6 ] =
10 - 3 + 1 + 2 - 6 =
13 - 9 =
= 4
3°) exemplo
-17 + { +5 - [ +2 - ( -6 +9 ) ]} =
-17 + { +5 - [ +2 + 6 - 9]} =
-17 + { +5 - 2 - 6 + 9 } =
-17 +5 - 2 - 6 + 9 =
-25 + 14 =
= - 11
EXERCICIOS
a) Calcule o valor das seguintes expressões :
1) 15 -(3-2) + ( 7 -4) = (R: 17)
2) 25 - ( 8 - 5 + 3) - ( 12 - 5 - 8) = (R: 20 )
3) ( 10 -2 ) - 3 + ( 8 + 7 - 5) = (R: 15)
4) ( 9 - 4 + 2 ) - 1 + ( 9 + 5 - 3) = (R: 17)
5) 18 - [ 2 + ( 7 - 3 - 8 ) - 10 ] = (R: 30 )
6) -4 + [ -3 + ( -5 + 9 - 2 )] = (R: -5)
7) -6 - [10 + (-8 -3 ) -1] = (R: -4)
8) -8 - [ -2 - (-12) + 3 ] = (R: -21)
9) 25 - { -2 + [ 6 + ( -4 -1 )]} = (R: 26)
10) 17 - { 5 - 3 + [ 8 - ( -1 - 3 ) + 5 ] } = (R: -2)
11) 3 - { -5 -[8 - 2 + ( -5 + 9 ) ] } = (R: 18)
12) -10 - { -2 + [ + 1 - ( - 3 - 5 ) + 3 ] } = (R: -20)
13) { 2 + [ 1 + ( -15 -15 ) - 2] } = (R: -29)
14) { 30 + [ 10 - 5 + ( -2 -3)] -18 -12} = (R: 0 )
15) 20 + { [ 7 + 5 + ( -9 + 7 ) + 3 ] } = (R: 33)
16) -4 - { 2 + [ - 3 - ( -1 + 7) ] + 2} = (R: 1)
17) 10 - { -2 + [ +1 + ( +7 - 3) - 2] + 6 } = (R: 3 )
18) -{ -2 - [ -3 - (-5) + 1 ]} - 18 = (R: -13)
19) -20 - { -4 -[-8 + ( +12 - 6 - 2 ) + 2 +3 ]} = (R: -15)
20) {[( -50 -10) + 11 + 19 ] + 20 } + 10 = (R: 0 )
MULTIPLICAÇÃO E DIVISÃO DE NÚMEROS INTEIROS
MULTIPLICAÇÃO
1) multiplicação de dois números de sinais iguais
observe o exemplo
a) (+5) . (+2) = +10
b) (+3) . (+7) = +21
c) (-5) . (-2) = +10
d) (-3) . (-7) = +21
conclusão: Se os fatores tiverem sinais iguais o produto é positivo
2) Multiplicação de dois produtos de sinais diferentes
observe os exemplos
a) (+3) . (-2) = -6
b) (-5) . (+4) = -20
c) (+6) . (-5) = -30
d) (-1) . (+7) = -7
Conclusão : Se dois produtos tiverem sinais diferentes o poduto é negativo
Regra pratica dos sinais na multiplicação
SINAIS IGUAIS: o resultado é positivo
a) (+) . (+) = (+)
b) (-) . (-) = (+)
SINAIS DIFERENTES: o resultado é negativo -
a) (+) . (-) = (-)
b) (-) . (+) = (-)
EXERCÍCIOS
1) Efetue as multiplicações
a) (+8) . (+5) = (R: 40)
b) (-8) . ( -5) = (R: 40)
c) (+8) .(-5) = (R: -40)
d) (-8) . (+5) = (R: -40)
e) (-3) . (+9) = (R: -27)
f) (+3) . (-9) = (R: -27)
g) (-3) . (-9) = (R: 27)
h) (+3) . (+9) = (R: 27)
i) (+7) . (-10) = (R: -70)
j) (+7) . (+10) = (R: 70)
l) (-7) . (+10) = (R: -70)
m) (-7) . (-10) = (R: 70)
n) (+4) . (+3) = (R: 12)
o) (-5) . (+7) = (R: -35)
p) (+9) . (-2) = (R: -18)
q) (-8) . (-7) = (R: 56)
r) (-4) . (+6) = (R: -24)
s) (-2) .(-4) = (R: 8 )
t) (+9) . (+5) = (R: 45)
u) (+4) . (-2) = (R: -8)
v) (+8) . (+8) = (R: 64)
x) (-4) . (+7) = (R: -28)
z) (-6) . (-6) = (R: 36)
2) Calcule o produto
a) (+2) . (-7) = (R: -14)
b) 13 . 20 = (R: 260)
c) 13 . (-2) = (R: -26)
d) 6 . (-1) = (R: -6)
e) 8 . (+1) = (R: 8)
f) 7 . (-6) = (R: -42)
g) 5 . (-10) = (R: -50)
h) (-8) . 2 = (R: -16)
i) (-1) . 4 = (R: -4)
j) (-16) . 0 = (R: 0)
MULTIPLICAÇAO COM MAIS DE DOIS NÚMEROS
Multiplicamos o primeiro número pelo segundo, o produto obtido pelo terceiro e assim sucessivamente, até o ultimo fator
exemplos
a) (+3) . (-2) . (+5) = (-6) . (+5) = -30
b) (-3) . (-4) . (-5) . (-6) = (+12) . (-5) . (-6) = (-60) . (-6) = +360
EXERCÍCIOS
1) Determine o produto:
a) (-2) . (+3) . ( +4) = (R: -24)
b) (+5) . (-1) . (+2) = (R: -10)
c) (-6) . (+5) .(-2) = (R: +60)
d) (+8) . (-2) .(-3) = (R: +48)
e) (+1) . (+1) . (+1) .(-1)= (R: -1)
f) (+3) .(-2) . (-1) . (-5) = (R: -30)
g) (-2) . (-4) . (+6) . (+5) = (R: 240)
h) (+25) . (-20) = (R: -500)
i) -36) .(-36 = (R: 1296)
j) (-12) . (+18) = (R: -216)
l) (+24) . (-11) = (R: -264)
m) (+12) . (-30) . (-1) = (R: 360)
2) Calcule os produtos
a) (-3) . (+2) . (-4) . (+1) . (-5) = (R: -120)
b) (-1) . (-2) . (-3) . (-4) .(-5) = (R: -120)
c) (-2) . (-2) . (-2) . (-2) .(-2) . (-2) = (R: 64)
d) (+1) . (+3) . (-6) . (-2) . (-1) .(+2)= (R: -72)
e) (+3) . (-2) . (+4) . (-1) . (-5) . (-6) = (R: 720)
f) 5 . (-3) . (-4) = (R: +60)
g) 1 . (-7) . 2 = (R: -14)
h) 8 . ( -2) . 2 = (R: -32)
i) (-2) . (-4) .5 = (R: 40)
j) 3 . 4 . (-7) = (R: -84)
l) 6 .(-2) . (-4) = (R: +48)
m) 8 . (-6) . (-2) = (R: 96)
n) 3 . (+2) . (-1) = (R: -6)
o) 5 . (-4) . (-4) = (R: 80)
p) (-2) . 5 (-3) = (R: 30)
q) (-2) . (-3) . (-1) = (R:-6)
r) (-4) . (-1) . (-1) = (R: -4)
3) Calcule o valor das expressões:
a) 2 . 3 - 10 = (R: -4)
b) 18 - 7 . 9 = (R: -45)
c) 3. 4 - 20 = (R: -8)
d) -15 + 2 . 3 = (R: -9)
e) 15 + (-8) . (+4) = (R: -17)
f) 10 + (+2) . (-5) = (R: 0 )
g) 31 - (-9) . (-2) = (R: 13)
h) (-4) . (-7) -12 = (R: 16)
i) (-7) . (+5) + 50 = (R: 15)
j) -18 + (-6) . (+7) = (R:-60)
l) 15 + (-7) . (-4) = (R: 43)
m) (+3) . (-5) + 35 = (R: 20)
4) Calcule o valor das expressões
a) 2 (+5) + 13 = (R: 23)
b) 3 . (-3) + 8 = (R: -1)
c) -17 + 5 . (-2) = (R: -27)
d) (-9) . 4 + 14 = (R: -22)
e) (-7) . (-5) - (-2) = (R: 37)
f) (+4) . (-7) + (-5) . (-3) = (R: -13)
g) (-3) . (-6) + (-2) . (-8) = (R: 34)
h) (+3) . (-5) - (+4) . (-6) = (R: 9)
PROPRIEDADES DA MULTIPLICAÇÃO
1) Fechamento: o produto de dois números inteiros é sempre um número inteiro.
exemplo: (+2) . (-5) = (-10)
2) Comultativa: a ordem dos fatores não altera o produto.
exemplo: (-3) . (+5) = (+5) . (-3)
3) Elemento Neutro: o número +1 é o elemento neutro da multiplicação.
Exemplos: (-6) . (+1) = (+1) . (-6) = -6
4) Associativa: na multiplicação de três números inteiros, podemos associar os dois primeiros ou os dois últimos, sem que isso altere o resultado.
exemplo: (-2) . [(+3) . (-4) ] = [ (-2) . (+3) ] . (-4)
5) Distributiva
exemplo: (-2) . [(-5) +(+4)] = (-2) . (-5) + (-2) . (+4)
DIVISÃO
Você sabe que a divisão é a operação inversa da multiplicação
Observe:
a) (+12) : (+4) = (+3) , porque (+3) . (+4) = +12
b) (-12) : (-4) = (+3) , porque (+3) . (-4) = -12
c) (+12) : (-4) = (-3) , porque (-3) . (-4) = +12
d) (-12) : (+4) = (-3), porque (-3) . (+4) = -12
REGRA PRÁTICA DOS SINAIS NA DIVISÃO
As regras de sinais na divisão é igual a da multiplicação:
SINAIS IGUAIS: o resultado é +
(+) : (+) = (+)
(-) : (-) = (-)
SINAIS DIFERENTES : o resultado é -
(+) : (-) = (-)
(-) : (+) = (-)
EXERCÍCIOS
1) Calcule o quocientes:
a) (+15) : (+3) = (R: 5 )
b) (+15) : (-3) = (R: -5)
c) (-15) : (-3) = (R: 5)
d) (-5) : (+1) = (R: -5)
e) (-8) : (-2) = (R: 4)
f) (-6) : (+2) = (R: -3)
g) (+7) : (-1) = (R: -7)
h) (-8) : (-8) = (R: 1)
f) (+7) : (-7) = (R: -1)
2) Calcule os quocientes
a) (+40) : (-5) = (R: -8)
b) (+40) : (+2) = (R: 20)
c) (-42) : (+7) = (R: -6)
d) (-32) : (-8)= (R: 4)
e) (-75) : (-15) = (R: 5)
f) (-15) : (-15) = (R: 1)
g) (-80) : (-10) = (R: 8)
h) (-48 ) : (+12) = (R: -4)
l) (-32) : (-16) = (R: 2)
j) (+60) : (-12) = (R: -5)
l) (-64) : (+16) = (R: -4)
m) (-28) : (-14) = (R: 2)
n) (0) : (+5) = (R: 0)
o) 49 : (-7) = (R: -7)
p) 48 : (-6) = (R: -8)
q) (+265) : (-5) = (R: -53)
r) (+824) : (+4) = (R: 206)
s) (-180) : (-12) = (R: 15)
t) (-480) : (-10) = (R: 48)
u) 720 : (-8) = (R: -90)
v) (-330) : 15 = (R: -22)
3) Calcule o valor das expressões
a) 20 : 2 -7 = (R: 3 )
b) -8 + 12 : 3 = (R: -4)
c) 6 : (-2) +1 = (R: -2)
d) 8 : (-4) - (-7) = (R: 5)
e) (-15) : (-3) + 7 = (R: 12)
f) 40 - (-25) : (-5) = (R: 35)
g) (-16) : (+4) + 12 = (R: 8)
h) 18 : 6 + (-28) : (-4) = ( R: 10)
i) -14 + 42 : 3 = (R: 0)
j) 40 : (-2) + 9 = (R: -11)
l) (-12) 3 + 6 = (R: 2)
m) (-54) : (-9) + 2 = (R: 8)
n) 20 + (-10) . (-5) = (R: 70)
o) (-1) . (-8) + 20 = (R: 28 )
p) 4 + 6 . (-2) = (R: -8)
q) 3 . (-7) + 40 = (R: 19)
r) (+3) . (-2) -25 = (R: -31)
s) (-4) . (-5) + 8 . (+2) = (R: 36)
t) 5: (-5) + 9 . 2 = (R: 17)
u) 36 : (-6) + 5 . 4 = (R: 14)
fonte:http://jmpmat13.blogspot.com.br
Observe que, no conjunto dos números naturais, a operação de subtração nem sempre é possivel
exemplos:
a) 5 - 3 = 2 (possível: 2 é um número natural)
b) 9 - 9 = 0 ( possível: 0 é um número natural)
c) 3 - 5 = ? ( impossível nos números naturais)
Para tonar sempre possível a subtração, foi criado o conjunto dos números inteiros relativos,
-1, -2, -3,.........
lê-se: menos um ou 1 negativo
lê-se: menos dois ou dois negativo
lê-se: menos três ou três negativo
Reunindo os números negativos, o zero e os números positivos, formamos o conjunto dos numeros inteiros relativos, que será representado por Z.
Z = { .....-3, -2, -1, 0, +1, +2, +3,......}
Importante: os números inteiros positivos podem ser indicados sem o sinal de +.
exemplo
a) +7 = 7
b) +2 = 2
c) +13 = 13
d) +45 = 45
Sendo que o zero não é positivo nem negativo
EXERCICIOS
1) Observe os números e diga:
-15, +6, -1, 0, +54, +12, -93, -8, +23, -72, +72
a) Quais os números inteiros negativos?
R: -15,-1,-93,-8,-72
b) Quais são os números inteiros positivos?
R: +6,+54,+12,+23,+72
2) Qual o número inteiro que não é nem positivo nem negativo?
R: É o zero
3) Escreva a leitura dos seguintes números inteiros:
a) -8 =(R: oito negativo)
b)+6 = (R: seis positivo)
c) -10 = (R: dez negativo)
d) +12 = (R: doze positivo)
e) +75 = (R: setenta e cinco positivo)
f) -100 = (R: cem negativo)
4) Quais das seguintes sentenças são verdadeiras?
a) +4 = 4 = ( V)
b) -6 = 6 = ( F)
c) -8 = 8 = ( F)
d) 54 = +54 = ( V)
e) 93 = -93 = ( F )
5) As temperaturas acima de 0°C (zero grau) são representadas por números positivos e as temperaturas abaixo de 0°C, por números negativos. Represente a seguinte situação com números inteiros relativos:
a) 5° acima de zero = (R: +5)
b) 3° abaixo de zero = (R: -3)
c) 9°C abaixo de zero= (R: -9)
d) 15° acima de zero = ( +15)
REPRESENTAÇÃO DOS NÚMEROS INTEIROS NA RETA
Vamos traçar uma reta e marcar o ponto 0. À direta do ponto 0, com uma certa unidade de medida, assinalemos os pontos que correspondem aos números positivos e à esquerda de 0, com a mesma unidade, assinalaremos os pontos que correspondem aos números negativos.
_I___I___I___I___I___I___I___I___I___I___I___I___I___I_
-6.. -5...-4. -3,. -2,..-1,.. 0,.+1,.+2,.+3,.+4,..+5,.+6
exercícios
1) Escreva os números inteiros:
a) compreendidos entre 1 e 7 (R: 2,3,4,5,6)
b) compreendidos entre -3 e 3 (R: -2,-1,0,1,2)
c) compreendidos entre -4 e 2 ( R: -3, -2, -1, 0, 1)
d) compreendidos entre -2 e 4 (R: -1, 0, 1, 2, 3 )
e) compreendidos entre -5 e -1 ( R: -4, -3, -2)
f) compreendidos entre -6 e 0 (R: -5, -4, -3, -2, -1)
2) Responda:
a) Qual é o sucessor de +8? (R: +9)
b) Qual é o sucessor de -6? (R: -5)
c) Qual é o sucessor de 0 ? (R: +1)
d) Qual é o antecessor de +8? (R: +7)
e) Qual é o antecessor de -6? ( R: -7)
f) Qual é o antecessor de 0 ? ( R: -1)
3) Escreva em Z o antecessor e o sucessor dos números:
a) +4 (R: +3 e +5)
b) -4 (R: -5 e - 3)
c) 54 (R: 53 e 55 )
d) -68 (R: -69 e -67)
e) -799 ( R: -800 e -798)
f) +1000 (R: +999 e + 1001)
NÚMEROS OPOSTOS E SIMÉTRICOS
Na reta numerada, os números opostos estão a uma mesma distancia do zero.
-I___I___I___I___I___I___I___I___I___I___I___I___I___I_
-6.. -5...-4. -3,. -2,..-1,.. 0,.+1,.+2,.+3,.+4,..+5,.+6
Observe que cada número inteiro, positivo ou negativo, tem um correspondente com sinais deferentes
exemplo
a) O oposto de +1 é -1.
b) O oposto de -3 é +3.
c) O oposto de +9 é -9.
d) O oposto de -5 é +5.
Obsevação: O oposto de zero é o próprio zero.
EXERCÍCIOS
1) Determine:
a) O oposto de +5 = (R:-5)
b) O oposto de -9 = (R: +9)
c) O oposto de +6 = (R: -6)
d) O oposto de -6 = (R: +6)
e) O oposto de +18 = (R: -18)
f) O oposto de -15 = (R: +15)
g) O oposto de +234= (R: -234)
h) O oposto de -1000 = (R: +1000)
COMPARAÇÃO DE NÚMEROS INTEIROS ,
Observe a representação gráfica dos números inteiros na reta.
-I___I___I___I___I___I___I___I___I___I___I___I___I___I_
-6.. -5...-4. -3,. -2,..-1,.. 0,.+1,.+2,.+3,.+4,..+5,.+6
Dados dois números quaisquer, o que está à direita é o mair deles, e o que está à esquerda, o menor deles.
exemplos
a) -1 maior; -4, poque -1 está à direita de -4.
b) +2 maior; -4, poque +2 está a direita de -4
c) -4 menor -2 , poque -4 está à esquerda de -2.
d) -2 menor +1, poque -2 está à esquerda de +1.
exercicios
1) Qual é o número maior ?
a) +1 ou -10 (R:+1)
b) +30 ou 0 (R: +30)
c) -20 ou 0 ( R: 0)
d) +10 ou -10 (R: +10)
e) -20 ou -10 (R: -10)
f) +20 ou -30 (R: +20)
g) -50 ou +50 (R:+50)
h) -30 ou -15 (R:-15)
2) compare os seguites pares de números, dizendo se o primeiro é maior, menor ou igual
a) +2 e + 3 (menor)
b) +5 e -5 (maior)
c) -3 e +4 (nenor)
d) +1 e -1 (maior)
e) -3 e -6 ( maior)
f) -3 e -2 (menor)
g) -8 e -2 (menor)
h) 0 e -5 (maior)
i) -2 e 0 (nenor)
j) -2 e -4 (maior)
l) -4 e -3 (menor)
m) 5 e -5 (maior)
n) 40 e +40 ( igual)
o) -30 e -10 (menor)
p) -85 e 85 (menor)
q) 100 e -200 (maior)
r) -450 e 300 (menor)
s) -500 e 400 (menor)
3) coloque os números em ordem crescente.
a) -9,-3,-7,+1,0 (R: -9,-7,-3,0,1)
b) -2, -6, -5, -3, -8 (R: -8, -6,-5, -3,-2)
c) 5,-3,1,0,-1,20 (R: -3,-1,0,1,5,20)
d) 25,-3,-18,+15,+8,-9 (R: -18,-9,-3,+8,+15,+25)
e) +60,-21,-34,-105,-90 ( R: -105,-90,-34,-21, +60)
f) -400,+620,-840,+1000,-100 ( R: -840,-400,-100,+620,+1000)
4) Coloque os números em ordem decrescente
a) +3,-1,-6,+5,0 (R: +5,+3,0,-1,-6)
b) -4,0,+4,+6,-2 ( R: +6,+4,0,-2,-4)
c) -5,1,-3,4,8 ( R: 8,4,1,-3,-5)
d) +10,+6,-3,-4,-9,+1 (R: +10,+6,+1,-3,-4,-9)
e) -18,+83,0,-172, -64 (R: +83,0,-18,-64,-172)
f) -286,-740, +827,0,+904 (R: +904,+827,0,-286,-740)
ADIÇÃO E SUBTRAÇÃO COM NÚMEROS INTEIROSADIÇÃO1) Adição de números positivos
A soma de dois números positivos é um número positivo.
EXEMPLO
a) (+2) + (+5) = +7
b) (+1) + (+4) = +5
c) (+6) + (+3) = +9
Simplificando a maneira de escrever
a) +2 +5 = +7
b) +1 + 4 = +5
c) +6 + 3 = +9
Observe que escrevemos a soma dos números inteiros sem colocar o sinal + da adição e eliminamos os parêteses das parcelas.
2) Adição de números negativos
A soma de dois numeros negativos é um número negativo
Exemplo
a) (-2) + (-3) = -5
b) (-1) + (-1) = -2
c) (-7) + (-2) = -9
Simplificando a maneira de escrever
a) -2 - 3 = -5
b) -1 -1 = -2
c) -7 - 2 = -9
Observe que podemos simplificar a maneira de escrever deixando de colocar o sinal de + na operação e eliminando os parênteses das parcelas.
EXERCÍCIOS
1) Calcule
a) +5 + 3 = (R:+8)
b) +1 + 4 = (R: +5)
c) -4 - 2 = (R: -6)
d) -3 - 1 = (R: -4)
e) +6 + 9 = (R: +15)
f) +10 + 7 = (R: +17)
g) -8 -12 = (R: -20)
h) -4 -15 = (R: -19)
i) -10 - 15 = (R: -25)
j) +5 +18 = (R: +23)
l) -31 - 18 = (R: -49)
m) +20 +40 = (R: + 60)
n) -60 - 30 = (R: -90)
o) +75 +15 = (R: +90)
p) -50 -50 = (R: -100)
2) Calcule:
a) (+3) + (+2) = (R: +5)
b) (+5) + (+1) = (R: +6)
c) (+7) + ( +5) = (R: +12)
d) (+2) + (+8) = (R: +10)
e) (+9) + (+4) = (R: +13)
f) (+6) + (+5) = (R: +11)
g) (-3) + (-2) = (R: -5)
h) (-5) + (-1) = (R: -6)
i) (-7) + (-5) = (R: -12)
j) (-4) + (-7) = (R: -11)
l) (-8) + ( -6) = (R: -14)
m) (-5) + ( -6) = (R: -11)
3) Calcule:
a) ( -22) + ( -19) = (R: -41)
b) (+32) + ( +14) = (R: +46)
c) (-25) + (-25) = (R: -50)
d) (-94) + (-18) = (R: -112)
e) (+105) + (+105) = (R: +210)
f) (-280) + (-509) = (R: -789)
g) (-321) + (-30) = (R: -350)
h) (+200) + (+137) = (R: +337)
3) Adição de números com sinais diferentes
A soma de dois números inteiros de sinais diferentes é obtida subtraindo-se os valores absolutos, dando-se o sinal do número que tiver maior valor absoluto.
exemplos
a) (+6) + ( -1) = +5
b) (+2) + (-5) = -3
c) (-10) + ( +3) = -7
simplificando a maneira de escrever
a) +6 - 1 = +5
b) +2 - 5 = -3
c) -10 + 3 = -7
Note que o resultado da adição tem o mesmo sinal que o número de maior valor absoluto
Observação:
Quando as parcelas são números opostos, a soma é igual a zero.
Exemplo
a) (+3) + (-3) = 0
b) (-8) + (+8) = 0
c) (+1) + (-1) = 0
simplificando a maneira de escrever
a) +3 - 3 = 0
b) -8 + 8 = 0
c) +1 - 1 = 0
4) Um dos numeros dados é zero
Quando um dos números é zero , a soma é igual ao outro número.
exemplo
a) (+5) +0 = +5
b) 0 + (-3) = -3
c) (-7) + 0 = -7
Simplificando a maneira de escrever
a) +5 + 0 = +5
b) 0 - 3 = -3
c) -7 + 0 = -7
exercícios
1) Calcule:
a) +1 - 6 = -5
b) -9 + 4 = -5
c) -3 + 6 = +3
d) -8 + 3 = -5
e) -9 + 11 = +2
f) +15 - 6 = +9
g) -2 + 14 = +12
h) +13 -1 = +12
i) +23 -17 = +6
j) -14 + 21 = +7
l) +28 -11 = +17
m) -31 + 30 = -1
2) Calcule:
a) (+9) + (-5) = +4
b) (+3) + (-4) = -1
c) (-8) + (+6) = -2
d) (+5) + (-9) = -4
e) (-6) + (+2) = -4
f) (+9) + (-1) = +8
g) (+8) + (-3) = +5
h) (+12) + (-3) = +9
i) (-7) + (+15) = +8
j) (-18) + (+8) = -10
i) (+7) + (-7) = 0
l) (-6) + 0 = -6
m) +3 + (-5) = -2
n) (+2) + (-2) = 0
o) (-4) +10 = +6
p) -7 + (+9) = +2
q) +4 + (-12) = -8
r) +6 + (-4) = +2
3) Calcule
a) (+5 + (+7) = +12
b) (-8) + (-9) = -17
c) (-37) + (+35) = -2
d) (+10) + (-9) = +1
e) (-15 ) + (+15) = 0
f) (+80) + 0 = +80
g) (-127) + (-51) = -178
h) (+37) + (+37) = +74
i) (-42) + (-18) = -60
j) (-18) + (+17) = -1
l) (-18) + (+19) = +1
m) (-1) + (-42) = -43
n) (+325) + (-257) = +68
o) 0 + (-75) = -75
p) (-121) + (+92) = -29
q ) (-578) + (-742) = -1320
r) (+101) + (-101) = 0
s) (-1050) + (+876) = -174
a) (+5 + (+7) = +12
b) (-8) + (-9) = -17
c) (-37) + (+35) = -2
d) (+10) + (-9) = +1
e) (-15 ) + (+15) = 0
f) (+80) + 0 = +80
g) (-127) + (-51) = -178
h) (+37) + (+37) = +74
i) (-42) + (-18) = -60
j) (-18) + (+17) = -1
l) (-18) + (+19) = +1
m) (-1) + (-42) = -43
n) (+325) + (-257) = +68
o) 0 + (-75) = -75
p) (-121) + (+92) = -29
q ) (-578) + (-742) = -1320
r) (+101) + (-101) = 0
s) (-1050) + (+876) = -174
PROPRIEDADE DA ADIÇÃO
1) Fechamento : a soma de dois números inteiros é sempre um número inteiro
exemplo (-4) + (+7) =( +3)
2) Comutativa: a ordem das parcelas não altera a soma.
exemplo: (+5) + (-3) = (-3) + (+5)
3) Elemento neutro: o número zero é o elemento neutro da adição.
exemplo: (+8) + 0 = 0 + (+8) = +8
4) Associativa: na adição de três números inteiros, podemos associar os dois primeiros ou os dois últimos, sem que isso altere o resultado.
exemplo: [(+8) + (-3) ] + (+4) = (+8) + [(-3) + (+4)]
5) Elemento oposto: qualquer número inteiro admite um simétrico ou oposto.
exemplo: (+7) + (-7) = 0
ADIÇÃO DE TRÊS OU MAIS NÚMEROS
Para obter a soma de três ou mais números adicionamos os dois primeiros e, em seguida, adicionamos esse resultado com o terceiro, e assim por diante.
exemplos
1) -12 + 8 - 9 + 2 - 6 =
= -4 - 9 + 2 - 6 =
= -13 + 2 - 6 =
= -11 - 6 =
= -17
2) +15 -5 -3 +1 - 2 =
= +10 -3 + 1 - 2 =
= +7 +1 -2 =
= +8 -2 =
= +6
Na adição de números inteiros podemos cancelar números opostos, poque a soma deles é zero.
INDICAÇÃO SIMPLIFICADA
a) podemos dispensar o sinal de + da primeira parcela quando esta for positiva.
exemplos
a) (+7) + (-5) = 7 - 5 = +2
b) (+6) + (-9) = 6 - 9 = -3
b) Podemos dispensar o sinal + da soma quando esta for positiva
exemplos
a) (-5) + (+7) = -5 + 7 = 2
b) (+9) + (-4) = 9 - 4 = 5
EXERCÍCIOS
1) Calcule
a) 4 + 10 + 8 = (R: 22)
b) 5 - 9 + 1 = (R: -3)
c) -8 - 2 + 3 = (R: -7)
d) -15 + 8 - 7 = (R: -14)
e) 24 + 6 - 12 = (R:+18)
f) -14 - 3 - 6 - 1 = (R: -24)
g) -4 + 5 + 6 + 3 - 9 = (R: + 1)
h) -1 + 2 - 4 - 6 - 3 - 8 = (R: -20)
i) 6 - 8 - 3 - 7 - 5 - 1 + 0 - 2 = (R: -20)
j) 2 - 10 - 6 + 14 - 1 + 20 = (R: +19)
l) -13 - 1 - 2 - 8 + 4 - 6 - 10 = (R: -36)
2) Efetue, cancelando os números opostos:
a) 6 + 4 - 6 + 9 - 9 = (R: +4)
b) -7 + 5 - 8 + 7 - 5 = (R: -8)
c) -3 + 5 + 3 - 2 + 2 + 1 = (R: +6)
d) -6 + 10 + 1 - 4 + 6= (R: +7)
e) 10 - 6 + 3 - 3 - 10 - 1 = (R: -7)
f) 15 - 8 + 4 - 4 + 8 - 15 = (R: 0)
3) Coloque em forma simplificada ( sem parênteses)
a) (+1) + (+4) +(+2) = (R: 1 +4 + 2)
b) (+1) + (+8) + (-2) = (R: 1 + 8 - 2)
c) (+5) +(-8) + (-1) = (R: +5 - 8 - 1)
d) (-6) + (-2) + (+1) = (R: -6 - 2 + 1)
4) Calcule:
a) (-2) + (-3) + (+2) = (R: -3)
b) (+3) + (-3) + (-5) = (R: -5)
c) (+1) + (+8) +(-2) = (R: +7 )
d) (+5) + (-8) + (-1) = (R: -4)
e) (-6) + (-2) + (+1) = (R: -7)
f) (-8) + ( +6) + (-2) = (R: -4)
g) (-7) + 6 + (-7) = (R: -8)
h) 6 + (-6) + (-7) = (R: -7)
i) -6 + (+9) + (-4) = (R: -1)
j) (-4) +2 +4 + (+1) = (R: +3)
5) Determine as seguintes somas
a) (-8) + (+10) + (+7) + (-2) = (R: +7)
b) (+20) + (-19) + (-13) + (-8) = (R: -20)
c) (-5) + (+8) + (+2) + (+9) = (R: +14)
d) (-1) + (+6) + (-3) + (-4) + (-5) = (R: -7)
e) (+10) + (-20) + (-15) + (+12) + (+30) + (-40) = (R: -23)
f) (+3) + (-6) + (+8) = (R: +5)
g) (-5) + (-12) + (+3) = (R: -14)
h) (-70) + (+20) + (+50) = (R: 0)
i) (+12) + (-25) + (+15) = (R: +2)
j) (-32) + (-13) + (+21) = (R: -24)
l) (+7) + (-5) + (-3) + (+10) = (R: +9)
m) (+12) + (-50) + (-8) + (+13) = (R: -33)
n) (-8)+(+4)+ (+8) + (-5) + (+3) = (R: +2)
o) (-36) + (-51) + (+100) + (-52) = (R: -39)
p) (+17) + (+13) + (+20) + (-5) + (-45) = (R:0)
6) Dados os números x= 6, y = 5 e z= -6, calcule
a) x + y = (R: +11)
b) y + z = (R: -4)
c) x + z = (R: -3)
SUBTRAÇÃO
A operação de subtração é uma operação inversa à da adição
Exemplos
a) (+8) - (+4) = (+8) + (-4) = = +4
b) (-6) - (+9) = (-6) + (-9) = -15
c) (+5) - (-2) = ( +5) + (+2) = +7
Conclusão: Para subtraimos dois números relativos, basta que adicionemos ao primeiro o oposto do segundo.
Observação: A subtração no conjunto Z tem apenas a propriedade do fechamento ( a subtração é sempre possivel)
ELIMINAÇÃO DE PARÊNTESES PRECEDIDOS DE SINAL NEGATIVO
Para facilitar o cálculo, eliminamos os parênteses usando o segnificado do oposto
veja:
a) -(+8) = -8 (significa o oposto de +8 é -8 )
b) -(-3) = +3 (significa o oposto de -3 é +3)
analogicamente:
a) -(+8) - (-3) = -8 +3 = -5
b) -(+2) - (+4) = -2 - 4 = -6
c) (+10) - (-3) - +3) = 10 + 3 - 3 = 10
conclusão: podemos eliminar parênteses precedidos de sinal negativo trocando-se o sínal do número que está dentro dos parênteses.
EXERCÍCIOS
1) Elimine os parênteses
a) -(+5) = -5
b) -(-2) = +2
c) - (+4) = -4
d) -(-7) = +7
e) -(+12) = -12
f) -(-15) = +15
g) -(-42) = +42
h) -(+56) = -56
2) Calcule:
a) (+7) - (+3) = (R: +4)
b) (+5) - (-2) = (R: +7)
c) (-3) - ( +8) = (R: -11)
d) (-1) -(-4) = (R: +3)
e) (+3) - (+8) = (R: -5)
f) (+9) - (+9) = (R: 0 )
g) (-8) - ( +5) = (R: -13)
h) (+5) - (-6) = (R: +11)
i) (-2) - (-4) = (R: +2)
j) (-7) - (-8) = (R: +1)
l) (+4) -(+4) = (R: 0)
m) (-3) - ( +2) = (R: -5)
n) -7 + 6 = (R: -1)
o) -8 -7 = (R: -15)
p) 10 -2 = (R: 8)
q) 7 -13 = (R: -6)
r) -1 -0 = (R: -1)
s) 16 - 20 = (R: -4)
t) -18 -9 = (R: -27)
u) 5 - 45 = (R:-40)
v) -15 -7 = (R: -22)
x) -8 +12 = (R: 4)
z) -32 -18 = (R:-50)
3) Calcule:
a) 7 - (-2) = (R: 9)
b) 7 - (+2) = (R: 5)
c) 2 - (-9) = (R: 11)
d) -5 - (-1) = (R: -4)
e) -5 -(+1) = (R: -6)
f) -4 - (+3) = (R: -7)
g) 8 - (-5) = (R: 13)
h) 7 - (+4) = (R: 3)
i) 26 - 45 = (R: -19)
j) -72 -72 = (R: -144)
l) -84 + 84 = (R: 0)
m) -10 -100 = (R: -110)
n) -2 -4 -1 = (R: -7)
o) -8 +6 -1 = (R: -3)
p) 12-7 + 3 = (R: 8)
q) 4 + 13 - 21 = (R: -4)
r) -8 +8 + 1 = (R: 1)
s) -7 + 6 + 9 = (R: 8)
t) -5 -3 -4 - 1 = (R: -13)
u) +10 - 43 -17 = (R: -50)
v) -6 -6 + 73 = (R: 61)
x) -30 +30 - 40 = (R: -40)
z) -60 - 18 +50 = (R: -28)
4) Calcule:
a) (-4) -(-2)+(-6) = (R: -8)
b) (-7)-(-5)+(-8) = (R: -10)
c) (+7)-(-6)-(-8) = (R: 21)
d) (-8) + (-6) -(+3) = (R: -17)
e) (-4) + (-3) - (+6) = (R: -13)
f) 20 - (-6) - (-8) = (R: 34)
g) 5 - 6 - (+7) + 1 = (R: -7)
h) -10 - (-3) - (-4) = (R: -3)
i) (+5) + (-8) = (R: -3)
j) (-2) - (-3) = (R: +1)
l) (-3) -(-9) = (R: +6)
m) (-7) - (-8) =(R: +1)
n) (-8) + (-6) - (-7) = (R: -7)
o) (-4) + (-6) + (-3) = (R: -13)
p) 15 -(-3) - (-1) = (R: +19)
q) 32 - (+1) -(-5) = (R: +36)
r) (+8) - (+2) = (R:+6)
s) (+15) - (-3) = (R: +18)
t) (-18) - (-10) = (R: -8)
u) (-25) - (+22) = (R:-47)
v) (-30) - 0 = (R: -30)
x) (+180) - (+182) = (R: -2)
z) (+42) - (-42) = (R: +84)
5) Calcule:
a) (-5) + (+2) - (-1) + (-7) = (R: -9)
b) (+2) - (-3) + (-5) -(-9) = (R: 9)
c) (-2) + (-1) -(-7) + (-4) = (R: 0)
d) (-5) + (-6) -(-2) + (-3) = (R: -12)
e) (+9) -(-2) + (-1) - (-3) = (R: 13)
f) 9 - (-7) -11 = (R: 5 )
g) -2 + (-1) -6 = (R: -9)
h) -(+7) -4 -12 = (R: -23)
i) 15 -(+9) -(-2) = (R: 8 )
j) -25 - ( -5) -30 = (R: -50)
l) -50 - (+7) -43 = (R: -100)
m) 10 -2 -5 -(+2) - (-3) = (R: 4)
n) 18 - (-3) - 13 -1 -(-4) = (R: 11)
o) 5 -(-5) + 3 - (-3) + 0 - 6 = (R: 10)
p) -28 + 7 + (-12) + (-1) -4 -2 = (R: -40)
q) -21 -7 -6 -(-15) -2 -(-10) = (R: -11)
r) 10 -(-8) + (-9) -(-12)-6 + 5 = (R: 20)
s) (-75) - (-25) = (R: -50)
t) (-75) - (+25) = (R: -100)
u) (+18) - 0 = (R: +18)
v) (-52) - (-52) = (R:0)
x) (-16)-(-25) = (R:+9)
z) (-100) - (-200) = (R:+100)
ELIMINAÇÃO DOS PARENTESES
1) parenteses precedidos pelo sinal +
Ao eliminarmos os parênteses e o sinal + que os precede, devemos conservar os sinais dos números contidos nesses parênteses.
exemplo
a) + (-4 + 5) = -4 + 5
b) +(3 +2 -7) = 3 +2 -7
2) Parênteses precedidos pelo sinal -
Ao eliminarmos os parênteses e o sinal de - que os precede, devemos trocar os sinais dos números contidos nesses parênteses.
exemplo
a) -(4 - 5 + 3) = -4 + 5 -3
b) -(-6 + 8 - 1) = +6 -8 +1
EXERCICIOS
1) Elimine os parênteses:
a) +(-3 +8) = (R: -3 + 8)
b) -(-3 + 8) = (R: +3 - 8)
c) +(5 - 6) = (R: 5 -6 )
d) -(-3-1) = (R: +3 +1)
e) -(-6 + 4 - 1) = (R: +6 - 4 + 1)
f) +(-3 -2 -1) = (R: -3 -2 -1 )
g) -(4 -6 +8) = (R: -4 +6 +8)
h) + (2 + 5 - 1) = (R: +2 +5 -1)
2) Elimine os parênteses e calcule:
a) + 5 + ( 7 - 3) = (R: 9)
b) 8 - (-2-1) = (R: 11)
c) -6 - (-3 +2) = (R: -5)
d) 18 - ( -5 -2 -3 ) = (R: 28)
e) 30 - (6 - 1 +7) = (R: 18)
f) 4 + (-5 + 0 + 8 -4) = (R: 3)
g) 4 + (3 - 5) + ( -2 -6) = (R: -6)
h) 8 -(3 + 5 -20) + ( 3 -10) = (R: 13)
i) 20 - (-6 +8) - (-1 + 3) = (R: 16)
j) 35 -(4-1) - (-2 + 7) = (R: 27)
3) Calcule:
a) 10 - ( 15 + 25) = (R: -30)
b) 1 - (25 -18) = (R: -6)
c) 40 -18 - ( 10 +12) = (R: 0)
d) (2 - 7) - (8 -13) = (R: 0 )
e) 7 - ( 3 + 2 + 1) - 6 = (R: -5)
f) -15 - ( 3 + 25) + 4 = (R: -39)
g) -32 -1 - ( -12 + 14) = (R: -35)
h) 7 + (-5-6) - (-9 + 3) = (R: 2)
i) -(+4-6) + (2 - 3) = (R: 1)
j) -6 - (2 -7 + 1 - 5) + 1 = (R: 4)
EXPRESSÕES COM NÚMEROS INTEIROS RELATIVOS
Lembre-se de que os sinais de associação são eliminados obedecendo à seguinte ordem:
1°) PARÊNTESES ( ) ;
2°) COLCHETES [ ] ;
3°) CHAVES { } .
Exemplos:
1°) exemplo
8 + ( +7 -1 ) - ( -3 + 1 - 5 ) =
8 + 7 - 1 + 3 - 1 + 5 =
23 - 2 = 21
2°) exemplo
10 + [ -3 + 1 - ( -2 + 6 ) ] =
10 + [ -3 + 1 + 2 - 6 ] =
10 - 3 + 1 + 2 - 6 =
13 - 9 =
= 4
3°) exemplo
-17 + { +5 - [ +2 - ( -6 +9 ) ]} =
-17 + { +5 - [ +2 + 6 - 9]} =
-17 + { +5 - 2 - 6 + 9 } =
-17 +5 - 2 - 6 + 9 =
-25 + 14 =
= - 11
EXERCICIOS
a) Calcule o valor das seguintes expressões :
1) 15 -(3-2) + ( 7 -4) = (R: 17)
2) 25 - ( 8 - 5 + 3) - ( 12 - 5 - 8) = (R: 20 )
3) ( 10 -2 ) - 3 + ( 8 + 7 - 5) = (R: 15)
4) ( 9 - 4 + 2 ) - 1 + ( 9 + 5 - 3) = (R: 17)
5) 18 - [ 2 + ( 7 - 3 - 8 ) - 10 ] = (R: 30 )
6) -4 + [ -3 + ( -5 + 9 - 2 )] = (R: -5)
7) -6 - [10 + (-8 -3 ) -1] = (R: -4)
8) -8 - [ -2 - (-12) + 3 ] = (R: -21)
9) 25 - { -2 + [ 6 + ( -4 -1 )]} = (R: 26)
10) 17 - { 5 - 3 + [ 8 - ( -1 - 3 ) + 5 ] } = (R: -2)
11) 3 - { -5 -[8 - 2 + ( -5 + 9 ) ] } = (R: 18)
12) -10 - { -2 + [ + 1 - ( - 3 - 5 ) + 3 ] } = (R: -20)
13) { 2 + [ 1 + ( -15 -15 ) - 2] } = (R: -29)
14) { 30 + [ 10 - 5 + ( -2 -3)] -18 -12} = (R: 0 )
15) 20 + { [ 7 + 5 + ( -9 + 7 ) + 3 ] } = (R: 33)
16) -4 - { 2 + [ - 3 - ( -1 + 7) ] + 2} = (R: 1)
17) 10 - { -2 + [ +1 + ( +7 - 3) - 2] + 6 } = (R: 3 )
18) -{ -2 - [ -3 - (-5) + 1 ]} - 18 = (R: -13)
19) -20 - { -4 -[-8 + ( +12 - 6 - 2 ) + 2 +3 ]} = (R: -15)
20) {[( -50 -10) + 11 + 19 ] + 20 } + 10 = (R: 0 )
MULTIPLICAÇÃO E DIVISÃO DE NÚMEROS INTEIROS
MULTIPLICAÇÃO
1) multiplicação de dois números de sinais iguais
observe o exemplo
a) (+5) . (+2) = +10
b) (+3) . (+7) = +21
c) (-5) . (-2) = +10
d) (-3) . (-7) = +21
conclusão: Se os fatores tiverem sinais iguais o produto é positivo
2) Multiplicação de dois produtos de sinais diferentes
observe os exemplos
a) (+3) . (-2) = -6
b) (-5) . (+4) = -20
c) (+6) . (-5) = -30
d) (-1) . (+7) = -7
Conclusão : Se dois produtos tiverem sinais diferentes o poduto é negativo
Regra pratica dos sinais na multiplicação
SINAIS IGUAIS: o resultado é positivo
a) (+) . (+) = (+)
b) (-) . (-) = (+)
SINAIS DIFERENTES: o resultado é negativo -
a) (+) . (-) = (-)
b) (-) . (+) = (-)
EXERCÍCIOS
1) Efetue as multiplicações
a) (+8) . (+5) = (R: 40)
b) (-8) . ( -5) = (R: 40)
c) (+8) .(-5) = (R: -40)
d) (-8) . (+5) = (R: -40)
e) (-3) . (+9) = (R: -27)
f) (+3) . (-9) = (R: -27)
g) (-3) . (-9) = (R: 27)
h) (+3) . (+9) = (R: 27)
i) (+7) . (-10) = (R: -70)
j) (+7) . (+10) = (R: 70)
l) (-7) . (+10) = (R: -70)
m) (-7) . (-10) = (R: 70)
n) (+4) . (+3) = (R: 12)
o) (-5) . (+7) = (R: -35)
p) (+9) . (-2) = (R: -18)
q) (-8) . (-7) = (R: 56)
r) (-4) . (+6) = (R: -24)
s) (-2) .(-4) = (R: 8 )
t) (+9) . (+5) = (R: 45)
u) (+4) . (-2) = (R: -8)
v) (+8) . (+8) = (R: 64)
x) (-4) . (+7) = (R: -28)
z) (-6) . (-6) = (R: 36)
2) Calcule o produto
a) (+2) . (-7) = (R: -14)
b) 13 . 20 = (R: 260)
c) 13 . (-2) = (R: -26)
d) 6 . (-1) = (R: -6)
e) 8 . (+1) = (R: 8)
f) 7 . (-6) = (R: -42)
g) 5 . (-10) = (R: -50)
h) (-8) . 2 = (R: -16)
i) (-1) . 4 = (R: -4)
j) (-16) . 0 = (R: 0)
MULTIPLICAÇAO COM MAIS DE DOIS NÚMEROS
Multiplicamos o primeiro número pelo segundo, o produto obtido pelo terceiro e assim sucessivamente, até o ultimo fator
exemplos
a) (+3) . (-2) . (+5) = (-6) . (+5) = -30
b) (-3) . (-4) . (-5) . (-6) = (+12) . (-5) . (-6) = (-60) . (-6) = +360
EXERCÍCIOS
1) Determine o produto:
a) (-2) . (+3) . ( +4) = (R: -24)
b) (+5) . (-1) . (+2) = (R: -10)
c) (-6) . (+5) .(-2) = (R: +60)
d) (+8) . (-2) .(-3) = (R: +48)
e) (+1) . (+1) . (+1) .(-1)= (R: -1)
f) (+3) .(-2) . (-1) . (-5) = (R: -30)
g) (-2) . (-4) . (+6) . (+5) = (R: 240)
h) (+25) . (-20) = (R: -500)
i) -36) .(-36 = (R: 1296)
j) (-12) . (+18) = (R: -216)
l) (+24) . (-11) = (R: -264)
m) (+12) . (-30) . (-1) = (R: 360)
2) Calcule os produtos
a) (-3) . (+2) . (-4) . (+1) . (-5) = (R: -120)
b) (-1) . (-2) . (-3) . (-4) .(-5) = (R: -120)
c) (-2) . (-2) . (-2) . (-2) .(-2) . (-2) = (R: 64)
d) (+1) . (+3) . (-6) . (-2) . (-1) .(+2)= (R: -72)
e) (+3) . (-2) . (+4) . (-1) . (-5) . (-6) = (R: 720)
f) 5 . (-3) . (-4) = (R: +60)
g) 1 . (-7) . 2 = (R: -14)
h) 8 . ( -2) . 2 = (R: -32)
i) (-2) . (-4) .5 = (R: 40)
j) 3 . 4 . (-7) = (R: -84)
l) 6 .(-2) . (-4) = (R: +48)
m) 8 . (-6) . (-2) = (R: 96)
n) 3 . (+2) . (-1) = (R: -6)
o) 5 . (-4) . (-4) = (R: 80)
p) (-2) . 5 (-3) = (R: 30)
q) (-2) . (-3) . (-1) = (R:-6)
r) (-4) . (-1) . (-1) = (R: -4)
3) Calcule o valor das expressões:
a) 2 . 3 - 10 = (R: -4)
b) 18 - 7 . 9 = (R: -45)
c) 3. 4 - 20 = (R: -8)
d) -15 + 2 . 3 = (R: -9)
e) 15 + (-8) . (+4) = (R: -17)
f) 10 + (+2) . (-5) = (R: 0 )
g) 31 - (-9) . (-2) = (R: 13)
h) (-4) . (-7) -12 = (R: 16)
i) (-7) . (+5) + 50 = (R: 15)
j) -18 + (-6) . (+7) = (R:-60)
l) 15 + (-7) . (-4) = (R: 43)
m) (+3) . (-5) + 35 = (R: 20)
4) Calcule o valor das expressões
a) 2 (+5) + 13 = (R: 23)
b) 3 . (-3) + 8 = (R: -1)
c) -17 + 5 . (-2) = (R: -27)
d) (-9) . 4 + 14 = (R: -22)
e) (-7) . (-5) - (-2) = (R: 37)
f) (+4) . (-7) + (-5) . (-3) = (R: -13)
g) (-3) . (-6) + (-2) . (-8) = (R: 34)
h) (+3) . (-5) - (+4) . (-6) = (R: 9)
PROPRIEDADES DA MULTIPLICAÇÃO
1) Fechamento: o produto de dois números inteiros é sempre um número inteiro.
exemplo: (+2) . (-5) = (-10)
2) Comultativa: a ordem dos fatores não altera o produto.
exemplo: (-3) . (+5) = (+5) . (-3)
3) Elemento Neutro: o número +1 é o elemento neutro da multiplicação.
Exemplos: (-6) . (+1) = (+1) . (-6) = -6
4) Associativa: na multiplicação de três números inteiros, podemos associar os dois primeiros ou os dois últimos, sem que isso altere o resultado.
exemplo: (-2) . [(+3) . (-4) ] = [ (-2) . (+3) ] . (-4)
5) Distributiva
exemplo: (-2) . [(-5) +(+4)] = (-2) . (-5) + (-2) . (+4)
DIVISÃO
Você sabe que a divisão é a operação inversa da multiplicação
Observe:
a) (+12) : (+4) = (+3) , porque (+3) . (+4) = +12
b) (-12) : (-4) = (+3) , porque (+3) . (-4) = -12
c) (+12) : (-4) = (-3) , porque (-3) . (-4) = +12
d) (-12) : (+4) = (-3), porque (-3) . (+4) = -12
REGRA PRÁTICA DOS SINAIS NA DIVISÃO
As regras de sinais na divisão é igual a da multiplicação:
SINAIS IGUAIS: o resultado é +
(+) : (+) = (+)
(-) : (-) = (-)
SINAIS DIFERENTES : o resultado é -
(+) : (-) = (-)
(-) : (+) = (-)
EXERCÍCIOS
1) Calcule o quocientes:
a) (+15) : (+3) = (R: 5 )
b) (+15) : (-3) = (R: -5)
c) (-15) : (-3) = (R: 5)
d) (-5) : (+1) = (R: -5)
e) (-8) : (-2) = (R: 4)
f) (-6) : (+2) = (R: -3)
g) (+7) : (-1) = (R: -7)
h) (-8) : (-8) = (R: 1)
f) (+7) : (-7) = (R: -1)
2) Calcule os quocientes
a) (+40) : (-5) = (R: -8)
b) (+40) : (+2) = (R: 20)
c) (-42) : (+7) = (R: -6)
d) (-32) : (-8)= (R: 4)
e) (-75) : (-15) = (R: 5)
f) (-15) : (-15) = (R: 1)
g) (-80) : (-10) = (R: 8)
h) (-48 ) : (+12) = (R: -4)
l) (-32) : (-16) = (R: 2)
j) (+60) : (-12) = (R: -5)
l) (-64) : (+16) = (R: -4)
m) (-28) : (-14) = (R: 2)
n) (0) : (+5) = (R: 0)
o) 49 : (-7) = (R: -7)
p) 48 : (-6) = (R: -8)
q) (+265) : (-5) = (R: -53)
r) (+824) : (+4) = (R: 206)
s) (-180) : (-12) = (R: 15)
t) (-480) : (-10) = (R: 48)
u) 720 : (-8) = (R: -90)
v) (-330) : 15 = (R: -22)
3) Calcule o valor das expressões
a) 20 : 2 -7 = (R: 3 )
b) -8 + 12 : 3 = (R: -4)
c) 6 : (-2) +1 = (R: -2)
d) 8 : (-4) - (-7) = (R: 5)
e) (-15) : (-3) + 7 = (R: 12)
f) 40 - (-25) : (-5) = (R: 35)
g) (-16) : (+4) + 12 = (R: 8)
h) 18 : 6 + (-28) : (-4) = ( R: 10)
i) -14 + 42 : 3 = (R: 0)
j) 40 : (-2) + 9 = (R: -11)
l) (-12) 3 + 6 = (R: 2)
m) (-54) : (-9) + 2 = (R: 8)
n) 20 + (-10) . (-5) = (R: 70)
o) (-1) . (-8) + 20 = (R: 28 )
p) 4 + 6 . (-2) = (R: -8)
q) 3 . (-7) + 40 = (R: 19)
r) (+3) . (-2) -25 = (R: -31)
s) (-4) . (-5) + 8 . (+2) = (R: 36)
t) 5: (-5) + 9 . 2 = (R: 17)
u) 36 : (-6) + 5 . 4 = (R: 14)
fonte:http://jmpmat13.blogspot.com.br
Assinar:
Comentários (Atom)